-
本文给出了一个可积的逆空时(逆空间-逆时间)非局部Sasa-Satsuma方程. 建立了这个方程的Darboux变换, 并且构造了这个逆空时非局部方程在零背景条件下的孤子解.
-
关键词:
- 可积的逆空时非局部Sasa-Satsuma方程 /
- 达布变换 /
- 孤子解
In this paper, we introduce an integrable reverse space-time nonlocal Sasa-Satsuma equation. The Darboux transformation and soliton solutions for this nonlocal integrable equation are constructed.-
Keywords:
- integrable reverse space-time nonlocal Sasa-Satsuma equation /
- Darboux transformation /
- soliton solution
[1] Sasa N, Satsuma J 1991 J. Phys. Soc. Jpn 60 409
Google Scholar
[2] Porsezian K, Nakkeeran K 1996 Phys. Rev. Lett 76 3955
Google Scholar
[3] Mihalache D, Torner L, Moldoveanu F, Panoiu N C, Truta N 1993 Phys. Rev. E 48 4699
Google Scholar
[4] Ghosh S, Kundu A, Nandy S 1999 J. Math. Phys. 40 1993
Google Scholar
[5] Li Y S, Han W T 2001 Chin. Ann. Math. 22B 171
[6] Gilson C, Hietarinta J, Nimmo J, Ohta Y 2003 Phys. Rev. E 68 016614
Google Scholar
[7] Wright O C 2007 Chaos, Solitons Fractals 33 374
[8] Nimmo J, Yilmaz H 2015 J. Phys. A. Math. Theor. 48 425202
Google Scholar
[9] Bandelow U, Akhmediev N 2012 Phys. Rev. E 86 026606
Google Scholar
[10] Li Z H, Li L, Tian H P, Zhou G S 2000 Phys. Rev. Lett. 84 4096
Google Scholar
[11] Ohta Y 2010 AIP Conference Proceeding 1212 114
[12] Zhao L C, Li S C, Ling L M 2014 Phys. Rev. E 89 023210
Google Scholar
[13] Xu T, Li M, Li L 2015 Europhys. Lett. 109 30006
Google Scholar
[14] Liu Y K, Li B 2017 Chin. Phys. Lett. 34 010202
Google Scholar
[15] Ablowitz M J, Musslimani Z H 2013 Phys. Rev. Lett. 110 064105
Google Scholar
[16] Ablowitz M J, Musslimani Z H 2016 Stud. Appl. Math. 139 7
[17] Ji J L, Zhu Z N 2017 Commun. Nonlinear Sci. Numer. Simul. 42 699
Google Scholar
[18] Lou S Y 2018 J. Math. Phys. 59 083507
Google Scholar
[19] Yang B, Yang J 2018 Stud. Appl. Math 140 178
Google Scholar
[20] Song C Q, Xiao D M, Zhu Z N 2017 J. Phys. Soc. Jpn. 86 054001
Google Scholar
[21] Rao J, Cheng Y, He J S 2017 Stud. Appl. Math. 139 568
Google Scholar
[22] Rao J, Cheng Y, Porsezian K, Mihalache S, He J S 2020 Physica D 401 132180
Google Scholar
[23] Ji J L, Zhu Z N 2017 J. Math. Anal. Appl. 453 973
Google Scholar
[24] Ma L Y, Zhu Z N 2016 J. Math. Phys. 57 083507
Google Scholar
-
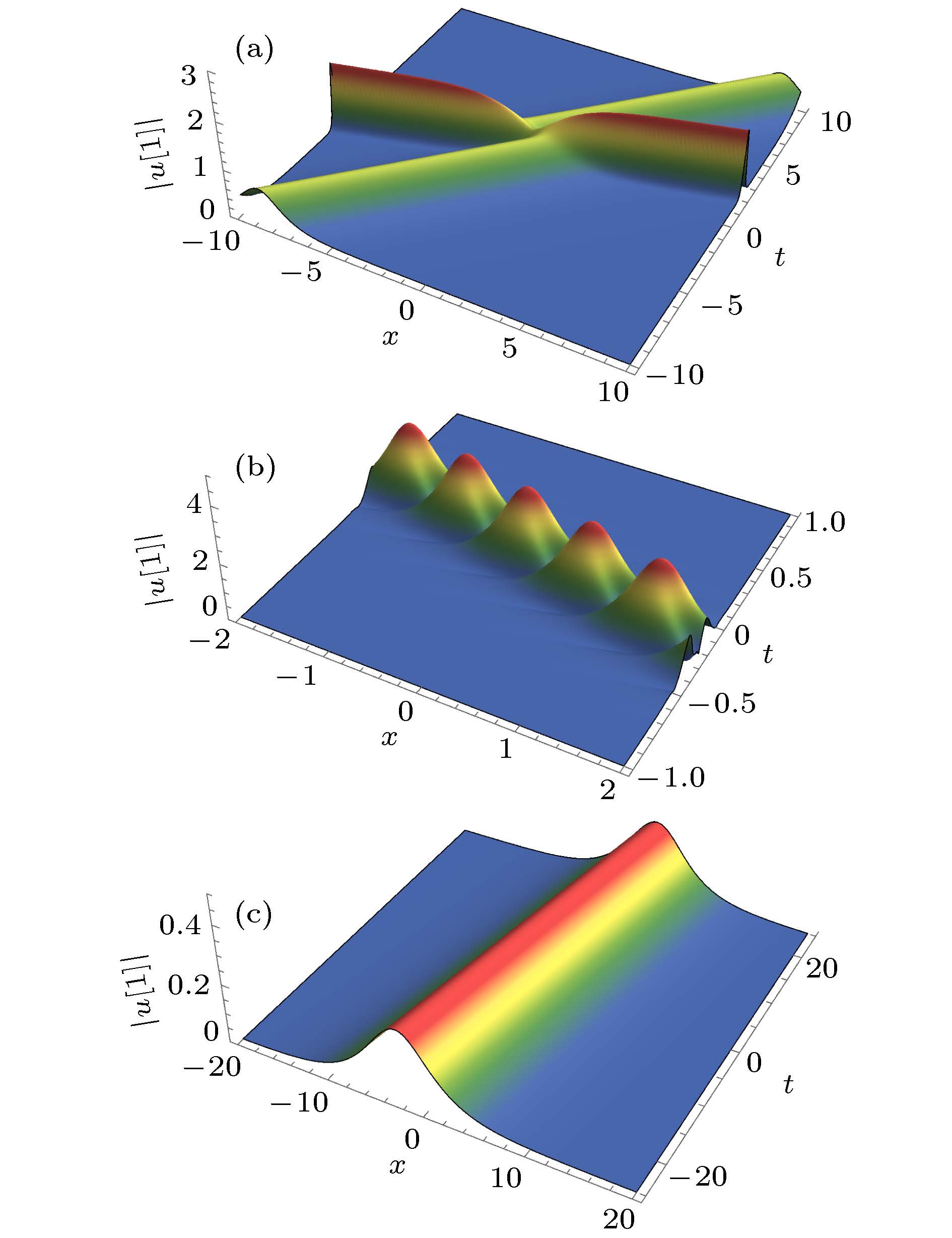
图 1 可积的逆空时非局部Sasa-Satsuma方程(7)的孤子解 (a) α1 = α2 = β1 = β2 =
$ \dfrac{\sqrt{2}}{2}, \lambda_1 = {\rm i}, \lambda_2 = -{\rm i}/2 $ ; (b) α1 = –α2 = β1 = –β2 =$ \dfrac{\sqrt{2}}{2}, \lambda_1 = 1+{\rm i}, \lambda_2 = 1-{\rm i} $ ; (c) α1 = β1 = 1, α2 = β2 = 0$\lambda_2 = {\rm i}, \lambda_1 = \dfrac{1-\sqrt{2}}{1+\sqrt{2}}\lambda_2 $ Fig. 1. Soliton solutions of integrable reverse space-time nonlocal Sasa-Satsuma equation (7): (a) α1 = α2 = β1 = β2 =
$ \dfrac{\sqrt{2}}{2}, \lambda_1 = {\rm i}, \lambda_2 = -{\rm i}/2 $ ; (b) α1 = –α2 = β1 = –β2 =$ \dfrac{\sqrt{2}}{2}, $ $\lambda_1 = 1+{\rm i}, \lambda_2 = 1-{\rm i} $ ; (c) α1 = β1 = 1, α2 = β2 = 0$\lambda_2 = {\rm i}, \lambda_1 = \dfrac{1-\sqrt{2}}{1+\sqrt{2}}\lambda_2 $ -
[1] Sasa N, Satsuma J 1991 J. Phys. Soc. Jpn 60 409
Google Scholar
[2] Porsezian K, Nakkeeran K 1996 Phys. Rev. Lett 76 3955
Google Scholar
[3] Mihalache D, Torner L, Moldoveanu F, Panoiu N C, Truta N 1993 Phys. Rev. E 48 4699
Google Scholar
[4] Ghosh S, Kundu A, Nandy S 1999 J. Math. Phys. 40 1993
Google Scholar
[5] Li Y S, Han W T 2001 Chin. Ann. Math. 22B 171
[6] Gilson C, Hietarinta J, Nimmo J, Ohta Y 2003 Phys. Rev. E 68 016614
Google Scholar
[7] Wright O C 2007 Chaos, Solitons Fractals 33 374
[8] Nimmo J, Yilmaz H 2015 J. Phys. A. Math. Theor. 48 425202
Google Scholar
[9] Bandelow U, Akhmediev N 2012 Phys. Rev. E 86 026606
Google Scholar
[10] Li Z H, Li L, Tian H P, Zhou G S 2000 Phys. Rev. Lett. 84 4096
Google Scholar
[11] Ohta Y 2010 AIP Conference Proceeding 1212 114
[12] Zhao L C, Li S C, Ling L M 2014 Phys. Rev. E 89 023210
Google Scholar
[13] Xu T, Li M, Li L 2015 Europhys. Lett. 109 30006
Google Scholar
[14] Liu Y K, Li B 2017 Chin. Phys. Lett. 34 010202
Google Scholar
[15] Ablowitz M J, Musslimani Z H 2013 Phys. Rev. Lett. 110 064105
Google Scholar
[16] Ablowitz M J, Musslimani Z H 2016 Stud. Appl. Math. 139 7
[17] Ji J L, Zhu Z N 2017 Commun. Nonlinear Sci. Numer. Simul. 42 699
Google Scholar
[18] Lou S Y 2018 J. Math. Phys. 59 083507
Google Scholar
[19] Yang B, Yang J 2018 Stud. Appl. Math 140 178
Google Scholar
[20] Song C Q, Xiao D M, Zhu Z N 2017 J. Phys. Soc. Jpn. 86 054001
Google Scholar
[21] Rao J, Cheng Y, He J S 2017 Stud. Appl. Math. 139 568
Google Scholar
[22] Rao J, Cheng Y, Porsezian K, Mihalache S, He J S 2020 Physica D 401 132180
Google Scholar
[23] Ji J L, Zhu Z N 2017 J. Math. Anal. Appl. 453 973
Google Scholar
[24] Ma L Y, Zhu Z N 2016 J. Math. Phys. 57 083507
Google Scholar
下载:
计量
- 文章访问数: 8141
- PDF下载量: 198
- 被引次数: 0
