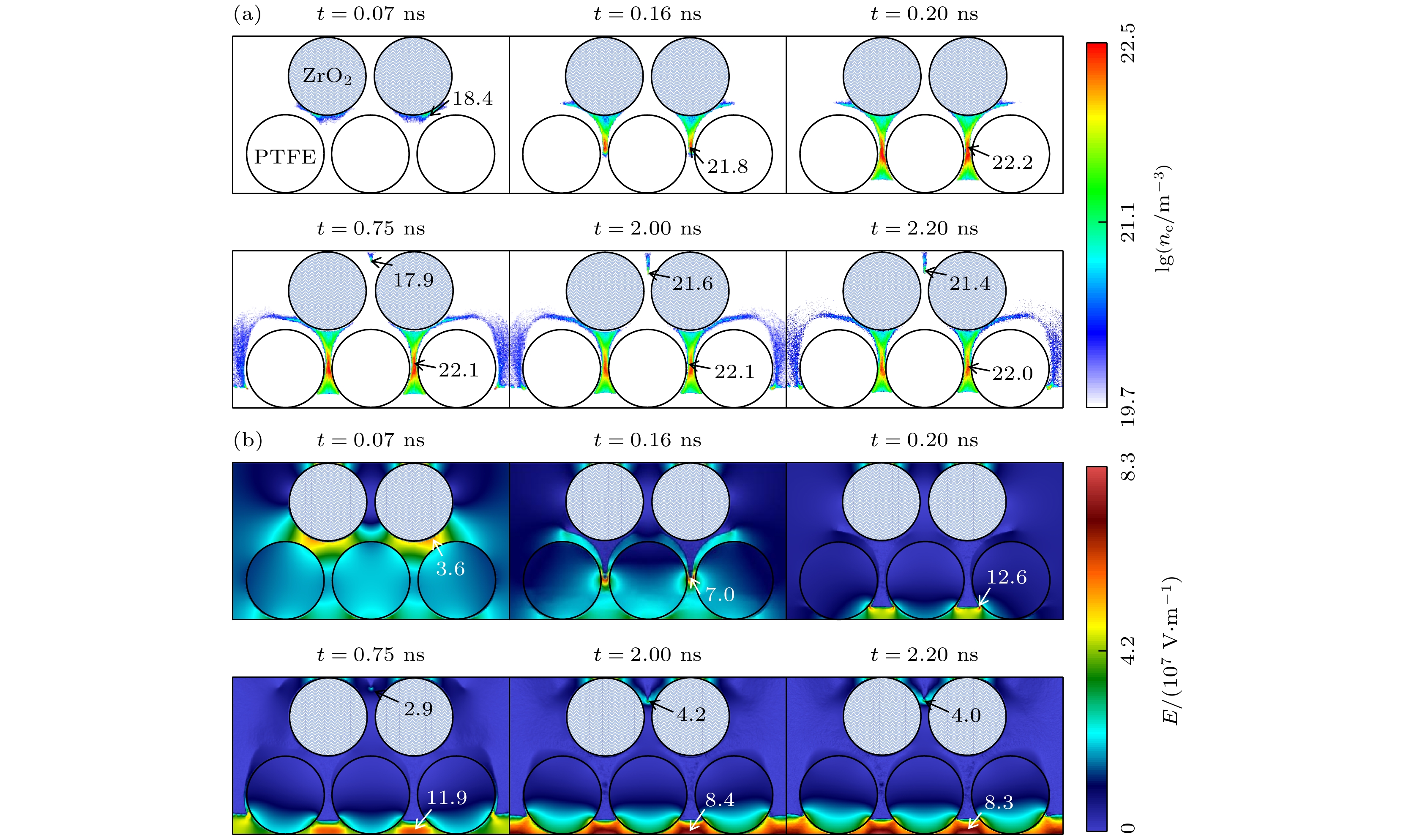
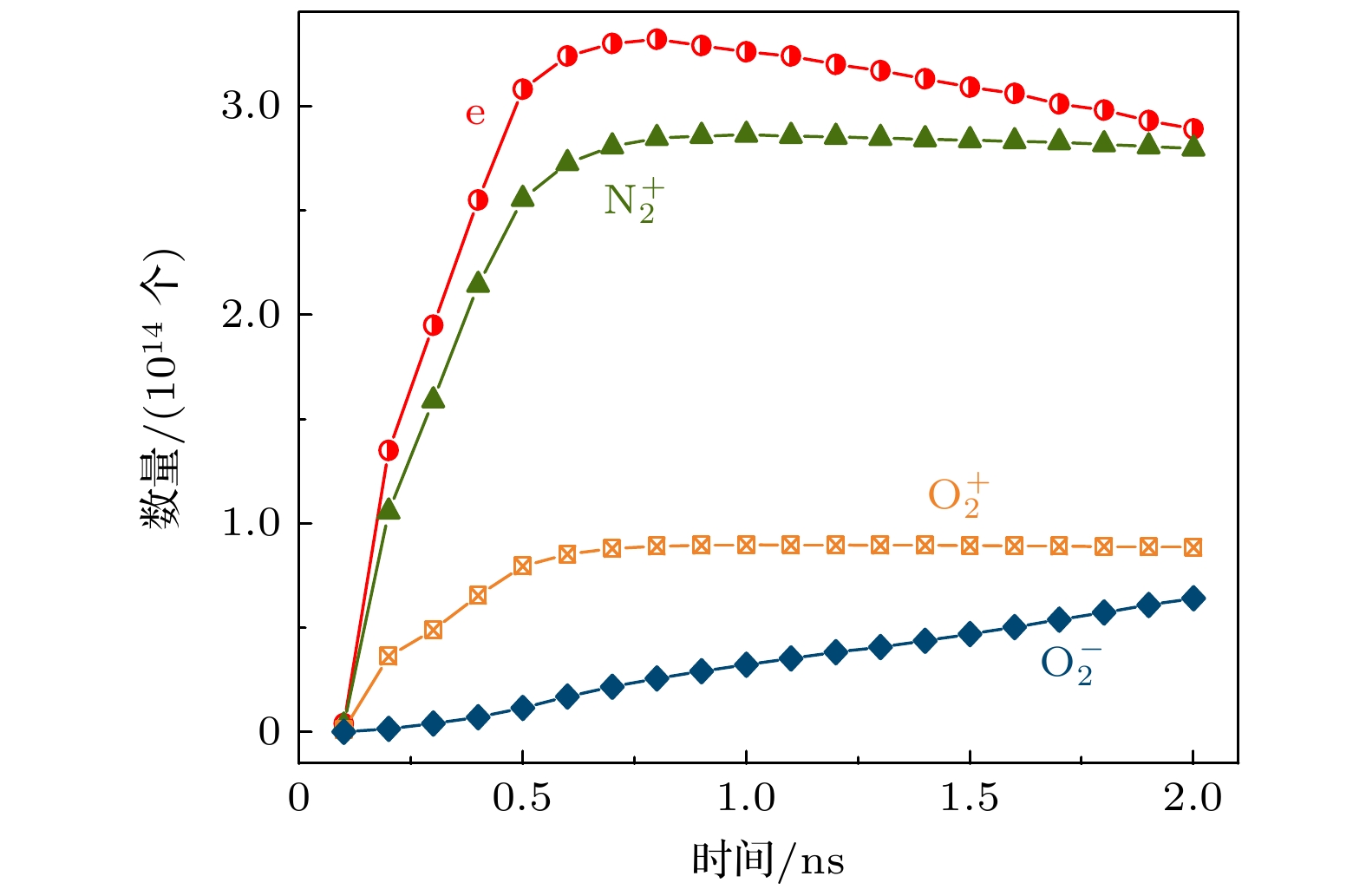
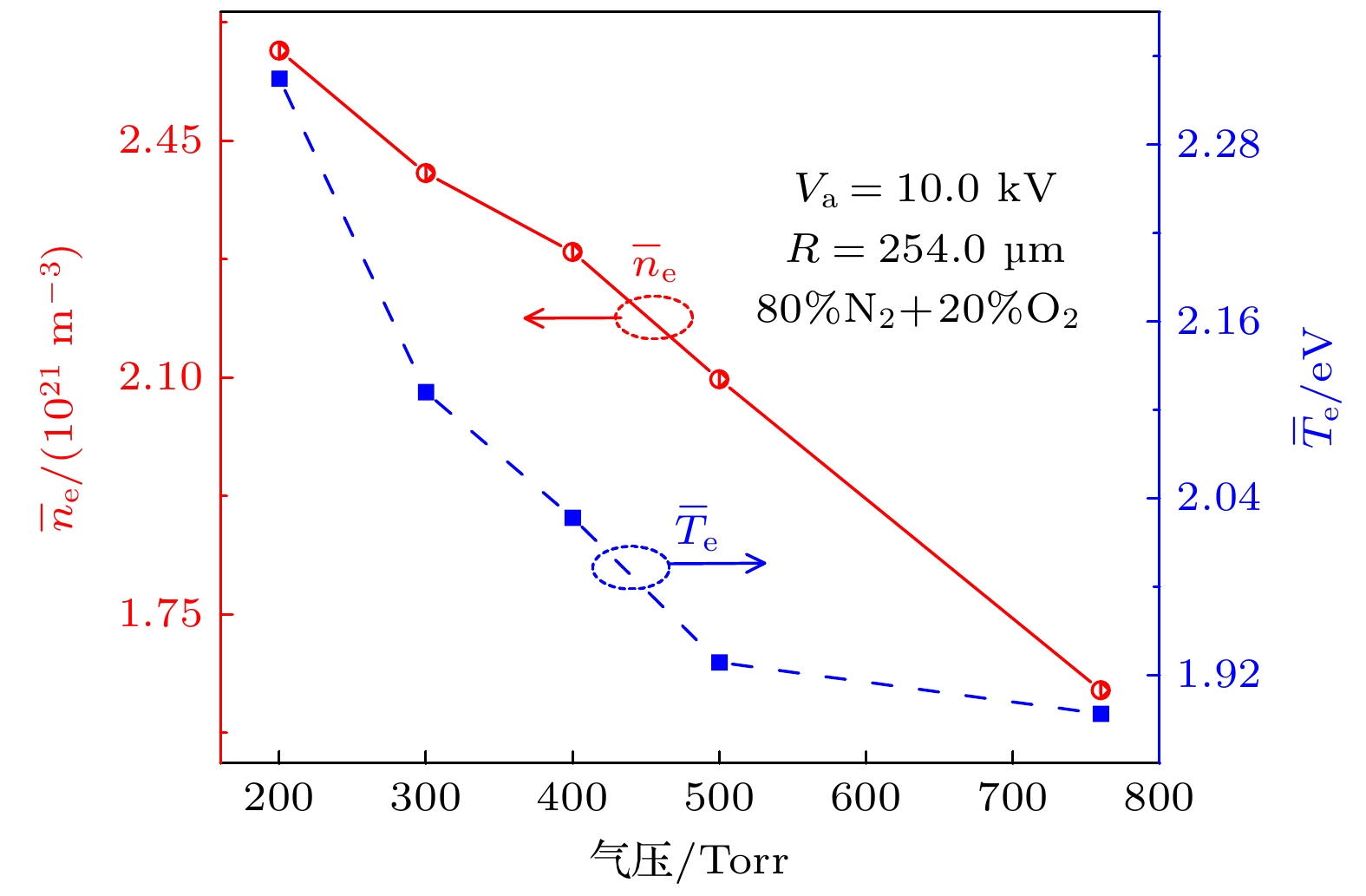
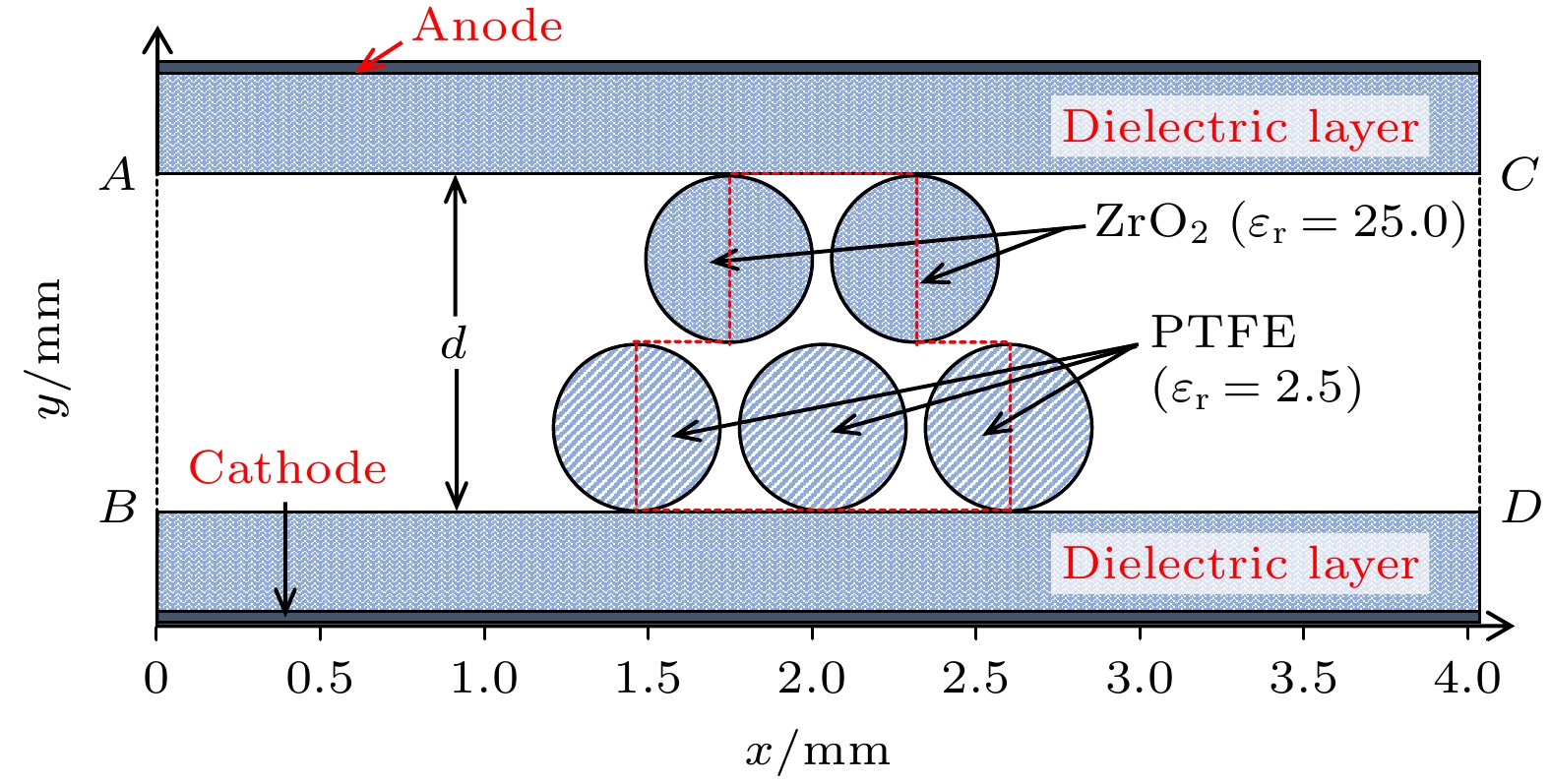
-
Packed bed dielectric barrier discharge (PB-DBD) is extremely popular in plasma catalysis applications, which can significantly improve the selectivity and energy efficiency of the catalytic processes. In order to achieve some complex chemical reactions, it is necessary to mix different materials in practical applications. In this work, by using the two-dimensional particle-in-cell/Monte Carlo collision (PIC/MCC) method, the discharge evolution in PB-DBD packed with two mixed dielectrics is numerically simulated to reveal the discharge characteristics. Due to the polarization of dielectric columns, the enhancement of electric field induces streamers at the bottom of the dielectric columns with high electrical permittivity (εr). The streamers propagate downward in the voids between the dielectric columns with low εr, which finally converts into volume discharges. Then, a new streamer forms near the upper dielectric plate and propagates downward along the void of the dielectric columns with high εr. Moreover, electron density between the columns with high εr is lower than that between the dielectric columns with low εr. In addition, the numbers of e, $ {\text{N}}_{2}^{+} $, $ {\text{O}}_{2}^{+} $ and $ {\text{O}}_{2}^{-} $ present different profiles versus time. All of e, $ {\text{N}}_{2}^{+} $ and $ {\text{O}}_{2}^{+} $ increase in number before 0.8 ns. After 0.8 ns, the number of electrons decreases with time, while the numbers of $ {\text{N}}_{2}^{+} $ and $ {\text{O}}_{2}^{+} $ keep almost constant. In the whole process, the number of $ {\text{O}}_{2}^{-} $ keeps increasing with time increasing. The reason for the different temporal profiles can be analyzed as follows. The sum of electrons deposited on the dielectric and those lost in attachment reaction is greater than the number of electrons generated by ionization reaction, resulting in the declining trend of electrons. Comparatively, the deposition of $ {\text{N}}_{2}^{+} $ and $ {\text{O}}_{2}^{+} $ on the dielectric almost balances with their generation, leading to the constant numbers of $ {\text{N}}_{2}^{+} $ and $ {\text{O}}_{2}^{+} $. In addition, the variation of averaged electron density ($ {\bar{n}}_{{\mathrm{e}}} $) and averaged electron temperature ($ {\bar{T}}_{{\mathrm{e}}} $) in the voids between the dielectric columns are also analyzed under different experimental parameters. Simulation results indicate that both of them decrease with pressure increasing or voltage amplitude falling. Moreover, they increase with dielectric column radius enlarging. In addition, $ {\bar{n}}_{{\mathrm{e}}} $ increases and then decreases with the increase of N2 content in the working gas, while $ {\bar{T}}_{{\mathrm{e}}} $ monotonically increases. The variations of $ {\bar{n}}_{{\mathrm{e}}} $ and $ {\bar{T}}_{{\mathrm{e}}} $ in the voids can be explained as follows. With the increase of pressure, the increase of collision frequency and the decrease of average free path lead to less energy obtained per unit time by electrons from the electric field, resulting in the decreasing of $ {\bar{T}}_{{\mathrm{e}}} $. Moreover, the first Townsend ionization coefficient decreases with the reduction in $ {\bar{T}}_{{\mathrm{e}}} $, resulting in less electrons produced per unit time. Hence, both $ {\bar{n}}_{{\mathrm{e}}} $ and $ {\bar{T}}_{{\mathrm{e}}} $ decrease with pressure increasing. Additionally, $ {\bar{T}}_{{\mathrm{e}}} $is mainly determined by electric field strength. Therefore, the rising voltage amplitude results in the increase of and $ {\bar{T}}_{{\mathrm{e}}} $. Based on the same reason for pressure, $ {\bar{n}}_{{\mathrm{e}}} $ also increases with the augment of voltage amplitude. Consequently, both $ {\bar{n}}_{{\mathrm{e}}} $ and $ {\bar{T}}_{{\mathrm{e}}} $ increase with voltage amplitude increasing. In addition, the surface area of dielectric columns increases with dielectric column radius enlarging. Therefore, more polarized charges are induced on the inner surface of the dielectric column, inducing a stronger electric field outside. Accordingly, the enlarging of dielectric column radius leads $ {\bar{n}}_{{\mathrm{e}}} $ and $ {\bar{T}}_{{\mathrm{e}}} $ to increase. Moreover, the variation of $ {\bar{n}}_{{\mathrm{e}}} $ with N2 content is analyzed from the ionization rate, and that of $ {\bar{T}}_{{\mathrm{e}}} $ is obtained by analyzing the ionization thresholds of N2 and O2.
-
Keywords:
- packed bed dielectric barrier discharge /
- particle-in-cell/Monte Carlo collision /
- dynamics /
- streamer
-
图 1 二维PB-DBD反应器示意图.
Figure 1. Schematic diagram of the two-dimensional PB-DBD reactor.
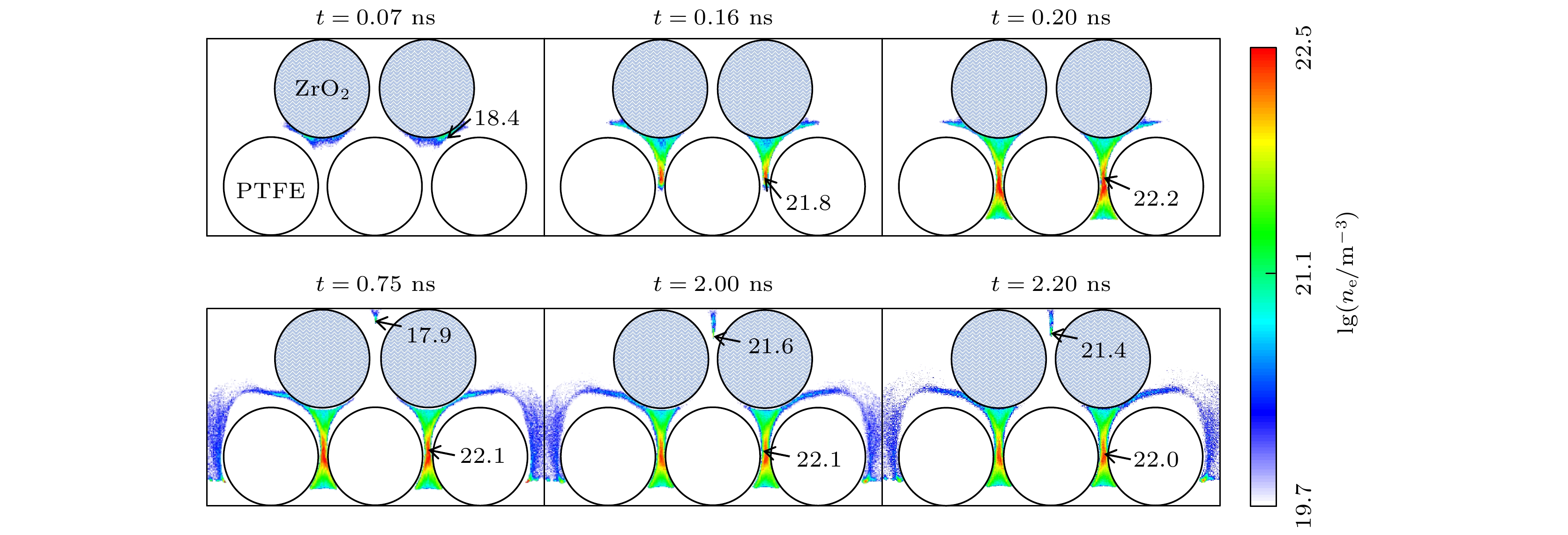
图 2 混合填充 ($ {\varepsilon }_{{\mathrm{r}}} $= 2.5和25.0) PB-DBD中ne (m–3) (a)和E (V/m) (b)的时空演化图, (a), (b)中的数值分别对应最大的lg (ne) 和E (×107)
Figure 2. Spatial-temporal evolution of ne (m–3) (a) and E (V/m) (b) in PB-DBD packed by mixed dielectric columns with $ {\varepsilon }_{{\mathrm{r}}} $= 2.5 and 25.0. The maximal (×107 V/m) values correspond to maximal lg (ne) and E (×107), respectively.
图 3 不同时刻的电子能量分布函数.
Figure 3. The electron energy distribution function at different discharge moments.
图 4 混合填充 ($ {\varepsilon }_{{\mathrm{r}}} $= 2.5和25.0) PB-DBD中e, $ {\text{N}}_{2}^{+} $, $ {\text{O}}_{2}^{+} $和$ {\text{O}}_{2}^{-} $数量随时间的变化
Figure 4. Numbers of e, $ {\text{N}}_{2}^{+} $, $ {\text{O}}_{2}^{+} $ and $ {\text{O}}_{2}^{-} $ versus time in PB-DBD packed by mixed dielectric columns with $ {\varepsilon }_{{\mathrm{r}}} $= 2.5 and 25.0.
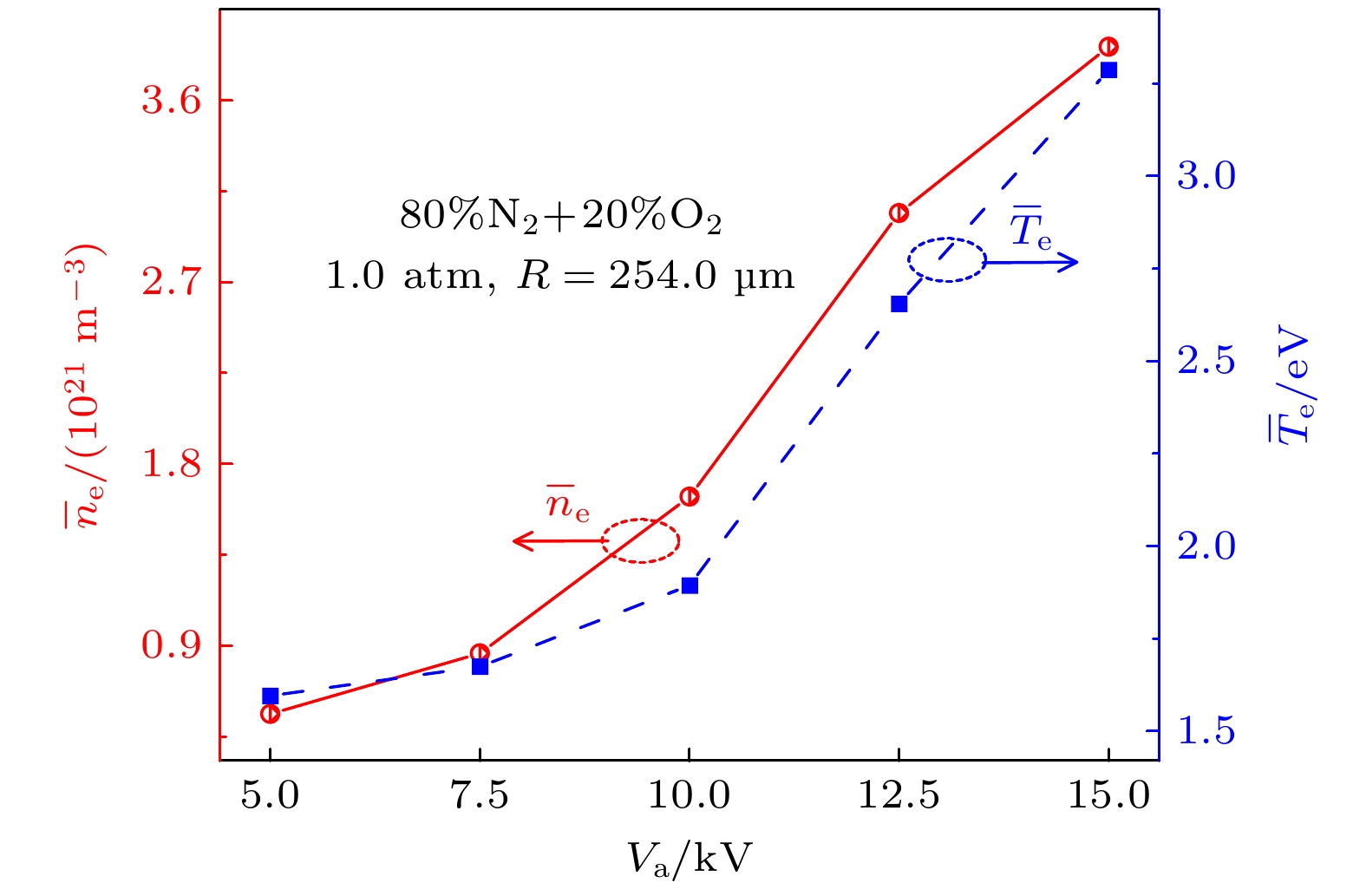
图 5 介质柱缝隙中平均电子密度($ {\bar{n}}_{{\mathrm{e}}} $)和平均电子温度($ {\bar{T}}_{{\mathrm{e}}} $)随气压的变化. 其中取平均的空间对应图1中红色虚线框内介质柱缝隙(白色区域)
Figure 5. Averaged electron density ($ {\bar{n}}_{{\mathrm{e}}} $) and averaged electron temperature ($ {\bar{T}}_{{\mathrm{e}}} $) as functions of pressure, the average is made in the voids between the dielectric columns surrounded by the red dashed lines (the white regions) in Fig. 1.
图 6 介质柱缝隙中$ {\bar{n}}_{{\mathrm{e}}} $和$ {\bar{T}}_{{\mathrm{e}}} $随电压幅值Va的变化, 其中取平均的空间与图5相同
Figure 6. The $ {\bar{n}}_{{\mathrm{e}}} $ and $ {\bar{T}}_{{\mathrm{e}}} $ in the voids between the dielectric columns as functions of Va, the voids are the same with those in Fig. 5.
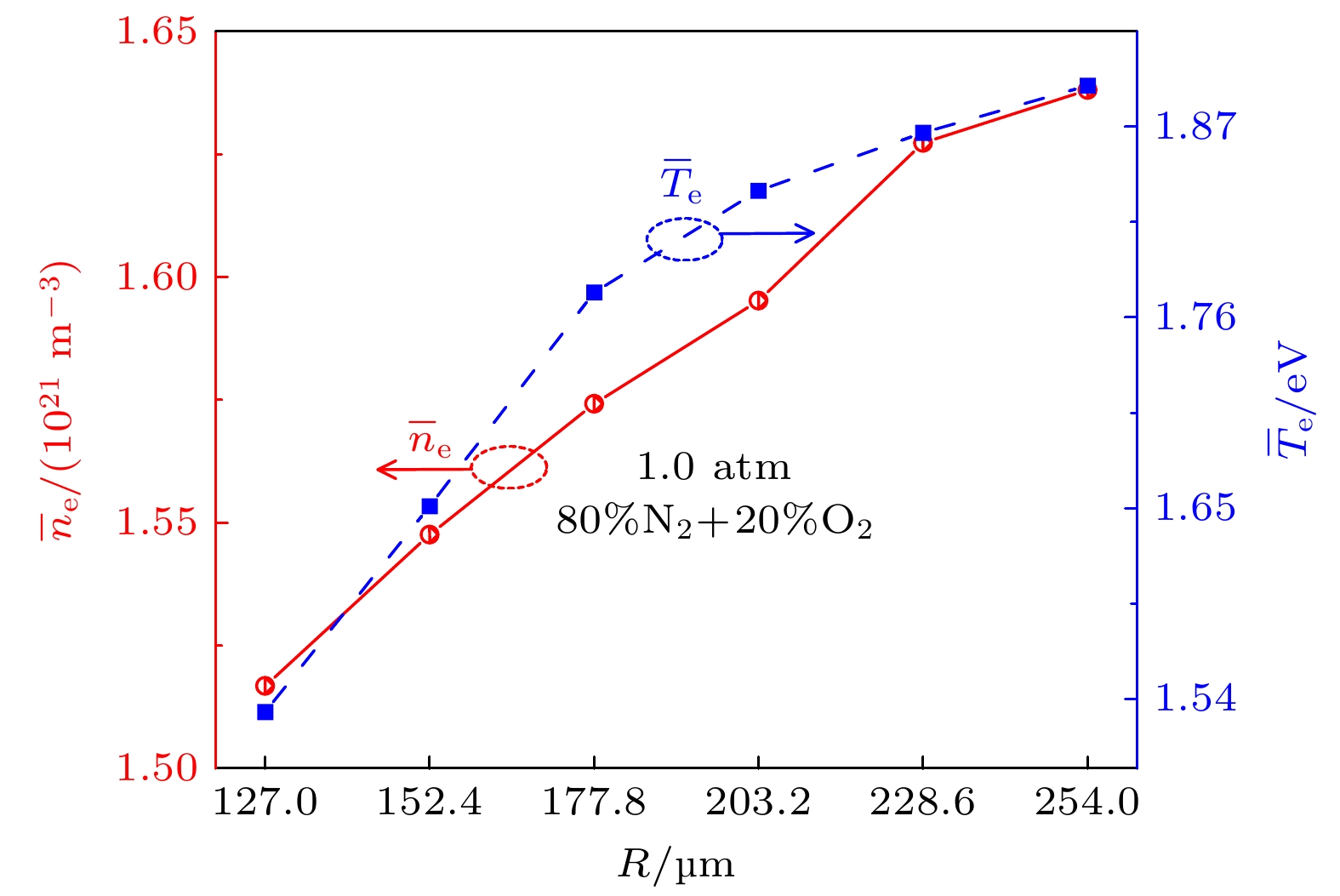
图 7 介质柱缝隙中$ {\bar{n}}_{{\mathrm{e}}} $和$ {\bar{T}}_{{\mathrm{e}}} $随介质柱半径 (R) 的变化关系. 其中取平均的空间与图5相同. 对于不同R, Va也成比例变化以保持外加电场不变
Figure 7. The $ {\bar{n}}_{{\mathrm{e}}} $ and $ {\bar{T}}_{{\mathrm{e}}} $ in the voids between the dielectric columns as functions of dielectric column radius (R), the voids are the same with those in Fig. 5. Va is varied for different R to keep applied E constant.
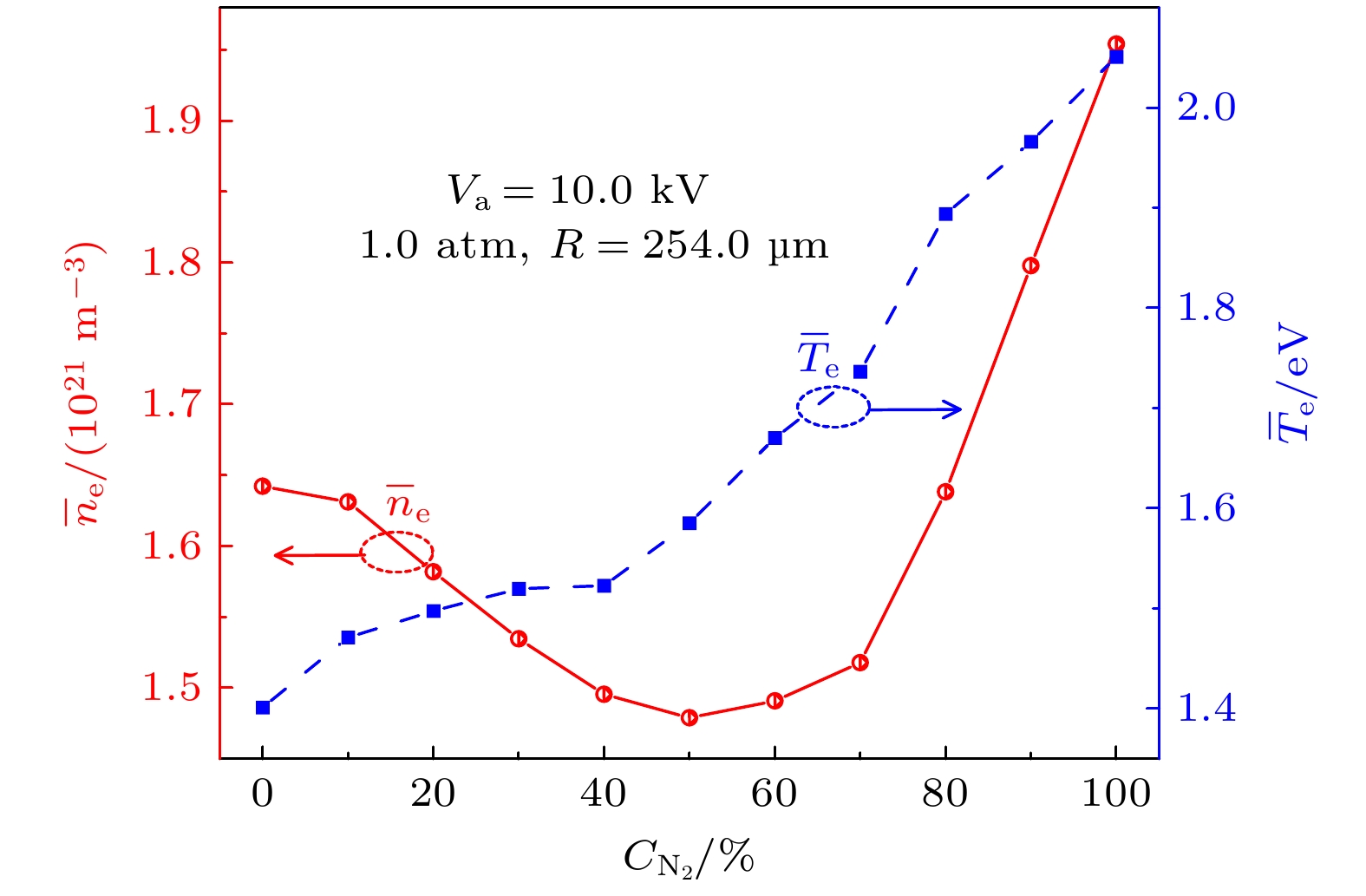
图 8 介质柱缝隙中$ {\bar{n}}_{{\mathrm{e}}} $和$ {\bar{T}}_{{\mathrm{e}}} $随混合气体中N2含量的变化关系, 其中取平均的空间与图5相同
Figure 8. The $ {\bar{n}}_{{\mathrm{e}}} $ and $ {\bar{T}}_{{\mathrm{e}}} $ in the voids between the dielectric columns as functions of N2 content in the mixture, the voids are the same with those in Fig. 5.
表 1 模型中所考虑的电子与N2和O2的碰撞.
Table 1. Collisions of electrons with neutral N2 and O2 considered in the model.
Reaction Threshold/eV Reference Electron-impact ionization [41,43–45] $ {\mathrm{e}}+{{\mathrm{O}}}_{2} $→$ 2 e+{{\mathrm{O}}}_{2}^{+} $ 12.06 $ {\mathrm{e}}+{{\mathrm{N}}}_{2} $→$ 2 e+{{\mathrm{N}}}_{2}^{+} $ 15.58 Attachment [41,43–45] $ {\mathrm{e}}+{{\mathrm{O}}}_{2}+{{\mathrm{O}}}_{2} $→$ {{\mathrm{O}}}_{2}^{-}+{{\mathrm{O}}}_{2} $ Elastic collision [43–45] $ {\mathrm{e}}+{{\mathrm{O}}}_{2} $→$ {\mathrm{e}}+{{\mathrm{O}}}_{2} $ $ {\mathrm{e}}+{{\mathrm{N}}}_{2} $→$ {\mathrm{e}}+{{\mathrm{N}}}_{2} $ Electron-impact excitation [43–45] $ {\mathrm{e}}+{{\mathrm{O}}}_{2} $→$ {\mathrm{e}}+{{\mathrm{O}}}_{2}^{{\mathrm{*}}} $ 0.98 $ {\mathrm{e}}+{{\mathrm{O}}}_{2} $→$ {\mathrm{e}}+{{\mathrm{O}}}_{2}^{{\mathrm{*}}} $ 1.63 $ {\mathrm{e}}+{{\mathrm{O}}}_{2} $→$ {\mathrm{e}}+{{\mathrm{O}}}_{2}^{{\mathrm{*}}} $ 6.0 $ {\mathrm{e}}+{{\mathrm{O}}}_{2} $→$ {\mathrm{e}}+{{\mathrm{O}}}_{2}^{{\mathrm{*}}} $ 8.4 $ {\mathrm{e}}+{{\mathrm{O}}}_{2} $→$ {\mathrm{e}}+{{\mathrm{O}}}_{2}^{{\mathrm{*}}} $ 10.0 $ {\mathrm{e}}+{{\mathrm{N}}}_{2} $→$ {\mathrm{e}}+{{\mathrm{N}}}_{2}^{{\mathrm{*}}} $ 6.169 $ {\mathrm{e}}+{{\mathrm{N}}}_{2} $→$ {\mathrm{e}}+{{\mathrm{N}}}_{2}^{{\mathrm{*}}} $ 7.353 $ {\mathrm{e}}+{{\mathrm{N}}}_{2} $→$ {\mathrm{e}}+{{\mathrm{N}}}_{2}^{{\mathrm{*}}} $ 7.362 $ {\mathrm{e}}+{{\mathrm{N}}}_{2} $→$ {\mathrm{e}}+{{\mathrm{N}}}_{2}^{{\mathrm{*}}} $ 8.165 $ {\mathrm{e}}+{{\mathrm{N}}}_{2} $→$ {\mathrm{e}}+{{\mathrm{N}}}_{2}^{{\mathrm{*}}} $ 8.399 $ {\mathrm{e}}+{{\mathrm{N}}}_{2} $→$ {\mathrm{e}}+{{\mathrm{N}}}_{2}^{{\mathrm{*}}} $ 8.549 $ {\mathrm{e}}+{{\mathrm{N}}}_{2} $→$ {\mathrm{e}}+{{\mathrm{N}}}_{2}^{{\mathrm{*}}} $ 8.89 $ {\mathrm{e}}+{{\mathrm{N}}}_{2} $→$ {\mathrm{e}}+{{\mathrm{N}}}_{2}^{{\mathrm{*}}} $ 9.7537 $ {\mathrm{e}}+{{\mathrm{N}}}_{2} $→$ {\mathrm{e}}+{{\mathrm{N}}}_{2}^{{\mathrm{*}}} $ 11.032 
DownLoad: CSV
表 2 电离速率与附着速率随混合气体中N2含量(10%, 40%, 60%, 90%)的变化
Table 2. Change of ionization rate and attachment rate with N2 content (10%, 40%, 60%, 90%) in mixed gas.
$ {C}_{{{\mathrm{N}}}_{2}} $/% kion/(m3·s–1) katt/(m3·s–1) 10 5.0×10–14 9.0×10–17 40 2.7×10–14 1.5×10–16 60 1.3×10–14 3.1×10–16 90 7.2×10–14 8.0×10–16
DownLoad: CSV
-
[1] Bogaerts A, Kozák T, Van Laer K, Snoeckx R 2015 Faraday Discuss. 183 271
[2] 陈少伟, 陈奕, 牛江奇, 刘天奇, 黄建国, 陈焕浩, 范晓雷 2024 化工进展 44
Chen S W, Chen Y, Niu J Q, Liu T Q, Huang J G, Chen H H, Fan X L 2024 Chem. Ind. Eng. Pro. 44
[3] 程 鹤, 雷孝廷, 张文超, 卢新培 2024 高电压技术 50 5206
Cheng H, Lei X T, Zhang W C, Lu X P 2024 High Volt. Eng. 50 5206
[4] 张海宝, 陈强 2021 70 095203
Google Scholar
Zhang H B, Chen Q 2021 Acta Phys. Sin. 70 095203
Google Scholar
[5] Lee S, Ha J, Li O L 2024 Nanomaterials 14 1313
Google Scholar
[6] Li J, Guo Q, Zhao X, Hu Y K, Zhang S Z, Zhao Y, Li S Z 2023 Mol. Catal. 549 113494
Google Scholar
[7] Zhang S, Gao Y, Sun H, Fan Z, Shao T 2022 High Volt. 7 e12201
[8] Hu G T, Ma Y C, Hao Q L, Liu D L, Dou B J, Bin F 2024 New J. Chem. 48 2624
Google Scholar
[9] Xu W C, Buelens L C, Galvita V V, Bogaerts A, Meynen V 2024 J. CO2 Util. 83 102820
Google Scholar
[10] Lv X, Zhang H P, Zhang H, Shao Y Y, Zhu J S 2024 Prog. Coat. 192 108499
Google Scholar
[11] Xu S S, Chansai S, Shao Y, Xu S J, Wang Y C, Haigh S, Mu Y B, Jiao Y L, Stere C E, Chen H H, Fan X L, Hardacre C 2020 Appl. Catal. B: Environ. 268 118752
Google Scholar
[12] Zhang S, Gao Y, Sun H, Fan Z, Shao T 2021 Plasma Sci. Technol. 23 064007
Google Scholar
[13] Michielsen I, Uytdenhouwen Y, Pype J, Michielsen B, Mertens J, Reniers F, Meynen V, Bogaerts A 2017 Chem. Eng. J. 326 477
Google Scholar
[14] Van Laer K, Bogaerts A 2017 Plasma Processes Polym. 14 1600129
Google Scholar
[15] Lu X P, Fang Z, Dai D, Shao T, Liu F, Zhang C, Liu D W, Nie L L, Jiang C Q 2023 High Volt. 8 1132
Google Scholar
[16] Ren C H, Huang B D, Luo Y, Zhang C, Shao T 2023 Plasma Chem. Plasma Process. 43 1613
Google Scholar
[17] Li S Q, Liu Y H, Yuan H, Liang J P, Zhang M, Li Y, Yang D Z 2022 Appl. Sci. 12 8895
Google Scholar
[18] Gómez-Ramírez A, Montoro-Damas A M, Cotrino J, Lambert R M, González-Elipe A R 2017 Plasma Processes Polym. 14 e1600081
Google Scholar
[19] Jiang N, Lu N, Shang K F, Li J, Wu Y 2013 J. Hazardous Mater. 262 387
Google Scholar
[20] Engeling K W, Kruszelnicki J, Kushner M J, Foster J E 2018 Plasma Sources Sci. Technol. 27 085002
Google Scholar
[21] Wang W Z, Butterworth T, Bogaerts A 2021 J. Phys. D: Appl. Phys. 54 214004
Google Scholar
[22] Li Y, Yang D Z, Qiao J J, Zhang L, Wang W Z, Zhao Z L, Zhou X F, Yuan H, Wang W C 2020 Plasma Sources Sci. Technol. 29 055004
Google Scholar
[23] Li X C, Zhang L L, Chen K, Ran J X, Pang X X, Jia P Y 2024 IEEE Trans. Plasma Sci. 52 1619
Google Scholar
[24] Van Laer K, Bogaerts A 2017 Plasma Sources Sci. Technol. 26 085007
Google Scholar
[25] Zhao P, Gu J G, Wang H Y, Zhang Y, Xu X Y, Jiang W 2020 Plasma Sci. Technol. 22 034013
Google Scholar
[26] Zhu M, Hu S Y, Wu F F, Ma H, Xie S Y, Zhang C H 2022 J. Phys. D: Appl. Phys. 55 225207
Google Scholar
[27] Zhu X B, Hu X L, Wu X Q, Cai Y X, Zhang H B, Tu X 2020 J. Phys. D: Appl. Phys. 53 164002
Google Scholar
[28] Jo S, Lee D H, Kang W S, Song Y H 2014 Phys. Plasmas 20 123507
[29] Li J, Zhu S J, Lu K, Ma C H, Yang D Z, Yu F 2021 J. Environ. Chem. Eng. 9 104654
Google Scholar
[30] Xiong R X, Zhao P, Wang H Y, Zhang Y, Jiang W 2020 J. Phys. D: Appl. Phys. 53 185202
Google Scholar
[31] Gadkari S, Gu S 2018 Phys. Plasmas 25 063513
Google Scholar
[32] Mujahid Z, Korolov I, Liu Y, Mussenbrock T, Schulze J 2022 J. Phys. D: Appl. Phys. 55 495201
Google Scholar
[33] 彭毅, 汪纯婧, 李晶, 高凯悦, 徐汉城, 陈传杰, 钱沐杨, 董冰岩, 王德真 2025 74 025202
Google Scholar
Peng Y, Wang C J, Li J, Gao K Y, Xu H C, Chen C J, Qian M Y, Dong B Y, Wang D Z 2025 Acta Phys. Sin. 74 025202
Google Scholar
[34] Kourtzanidis, K 2023 Plasma Sources Sci. Technol. 32 105016
Google Scholar
[35] Liu J, Zhu X B, Hu X L, Tu X 2022 Plasma Sci. Technol. 24 025503
Google Scholar
[36] Kang W S, Kim H H, Teramoto Y, Ogata A, Lee J Y, Kim D W, Hur M, Song Y H 2018 Plasma Sources Sci. Technol. 27 015018
Google Scholar
[37] Van Laer K, Bogaerts A 2016 Plasma Sources Sci. Technol. 25 015002
Google Scholar
[38] Li S J, Yu X, Dang X Q, Wang P Y, Meng X K, Wang Q, Hou H 2022 J. Clean. Prod. 340 130774
Google Scholar
[39] Li S J, Yu X, Dang X Q, Wang P Y, Meng X K, Zheng H C 2022 Plasma Sci. Technol. 24 015504
Google Scholar
[40] Gao M X, Zhang Y, Wang H Y, Guo B, Zhang Q Z, Bogaerts A 2018 Catal. 8 248
[41] Zhang Y, Wang H Y, Zhang Y R, Bogaerts A 2017 Plasma Sources Sci. Technol. 26 054002
Google Scholar
[42] Zhang Q Z, Zhang L, Yang D Z, Schulze J, Wang Y N, Bogaerts A 2020 Plasma Processes Polym. 18 e2000234
[43] Zuo X, Zhou Y Y, Zhang Q Z, Wang H Y, Li Z H, Zhu J Z, Jiang X W, Zhang Y 2022 Plasma Processes Polym. 19 e2200025
Google Scholar
[44] Biagi V8.9 Database. [Online]. 2015 Available: https://www.lxcat.net
[45] Gu J G, Zhang Y, Gao M X, Wang H Y, Zhang Q Z, Yi L, Jiang W 2019 J. Appl. Phys. 125 153303
Google Scholar
[46] Zhang Y, Wang H Y, Jiang W, Bogaerts A 2015 New J. Phys. 17 083056
Google Scholar
[47] Kuhfeld J, Lepikhin N D, Luggenholscher D, Gzarnetzki U, Donko Z 2023 Plasma Sources Sci. Technol. 32 084001
Google Scholar
[48] 石峰, 王昊, 朱红伟 2018 真空与低温 24 188
Google Scholar
Shi F, Wang H, Zhu H W 2018 Vacuum Cryogenics 24 188
Google Scholar
[49] Zhang L Y, Zhang Q Z, Mujahid Z U, Neuroth C, Berger B, Schulze J 2024 Plasma Sources Sci. Technol. 33 105016
Google Scholar
[50] Meierbachtol C S, Greenwood A D, Verboncoeur J P, Shanker B 2015 IEEE Trans. Plasma Sci. 43 3778
Google Scholar
[51] Raizer Y P, Kisin V I, Allen J E 1991 Gas Discharge Physics (Heidelberg: Springer
[52] Naidis G V 2011 Appl. Sci. 38 141501
[53] Rad R H, Brüser V, Schiorlin M, Schäfer J, Brandenburg R 2023 Chem. Eng. J. 456 141072
Google Scholar
[54] Mei D H, Zhu X B, He Y L, Yan J D, Tu X 2015 Plasma Sources Sci. Technol. 24 015011
[55] Wang X B, Zhu C Y, Wang L, Liu J Q, Jin A 2022 Radiat. Eff. Defect. S. 177 1117
[56] 张雪雪, 贾鹏英, 冉俊霞, 李金懋, 孙焕霞, 李雪辰 2024 73 085201
Google Scholar
Zhang X X, Jia P Y, Ran J X, Li J M, Sun H X, Li X C 2024 Acta Phys. Sin. 73 085201
Google Scholar
[57] Cui Z L, Zhou C, Jafarzadeh A, Meng S Y, Yi Y H, Wang Y F, Zhang X X, Hao Y P, Li L C, Bogaerts A 2022 High Volt. 7 1048
Google Scholar
[58] Kumar P, Saha S K, Sharma A 2023 Chem. Eng. S. 282 119372
Google Scholar
[59] Chachereau A, Pancheshnyi S 2014 IEEE Trans. Plasma Sci. 42 3328
Google Scholar
DownLoad:
Metrics
- Abstract views: 322
- PDF Downloads: 10
- Cited By: 0
