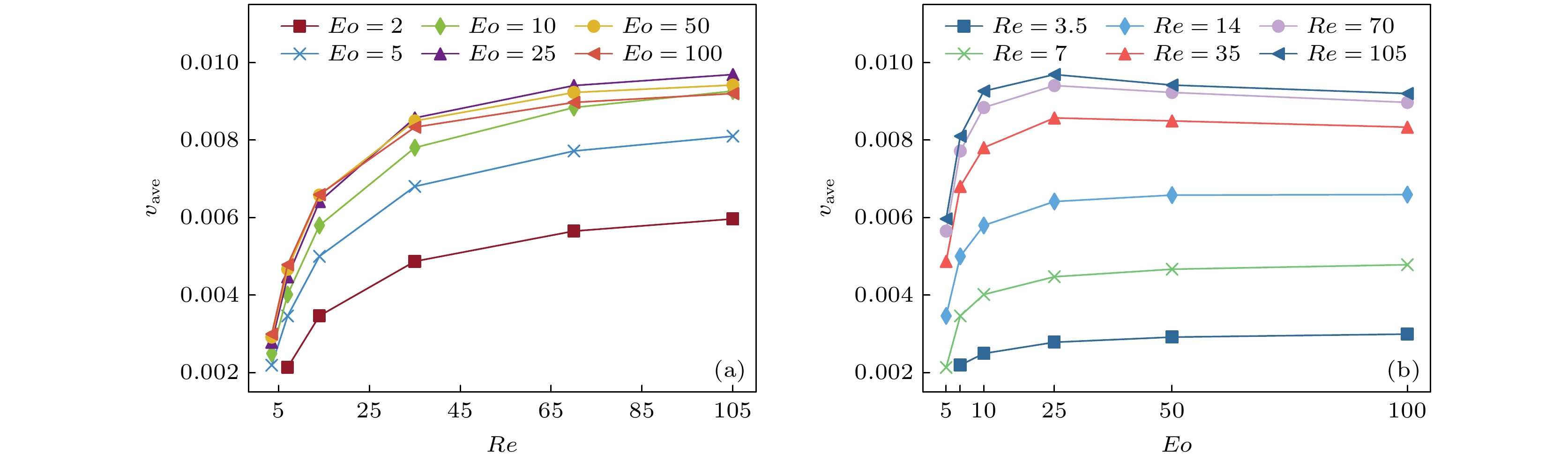
-
In this paper, a three-dimensional numerical simulation of the motion behavior of bubbles in complex porous medium channels in a large density ratio gas-liquid system is conducted based on the lattice Boltzmann method. The Eötvös number (Eo), contact angle (θ) and Reynolds number (Re) are systematically discussed with emphasis on the law of their coupling effect affecting bubble velocity, morphological evolution and stagnation phenomenon. The results show that the increase of contact angle will reduce the bubble velocity but intensify the velocity fluctuations, making the bubbles tend flat, while the increase of Eo number significantly suppresses the influence of the contact angle, stabilizes the bubble velocity, and makes its shape close to a bullet head shape. When the contact angle is large (θ>90°) and the Eo number is small (Eo<10), the adhesion force is significantly enhanced and the bubbles will stagnate inside the porous medium. Re number and contact angle compete in the generation of resistance, and have mutually reinforcing effects on the average velocity of bubbles and interface evolution. The larger contact angle makes the deformation of the bubble tail intensify and becomes unstable, and as the Re number further increases, the tail tentacles are more likely to break, forming residual bubbles. It is also found in this work that the coupling between Eo number and Re number significantly affects bubble behavior in motion and morphological evolution. Under the conditions of high Eo number (Eo≥25) and high Re number (Re≥14), the bubble velocity increases with the Eo number rising, and the trend becomes more significant as the Re number increases; while under the conditions of low Eo number (Eo<25) and low Re number (Re<14), the speed change pattern is completely opposite. This phenomenon is due to the high instability of bubble morphology under the conditions of high Eo number and high Re number, which affects the buoyancy and speed performance. The research results provide important guidance for optimizing the flow behavior of bubbles in porous medium.
-
Keywords:
- lattice Boltzmann method /
- gas-liquid two-phase flow /
- porous medium /
- three-dimensional numerical simulation
-
图 1 三维物理模型 (a) 示意图; (b) y方向正视图
Figure 1. 3D physical model (a) Schematic diagram; (b) front view in the y direction.
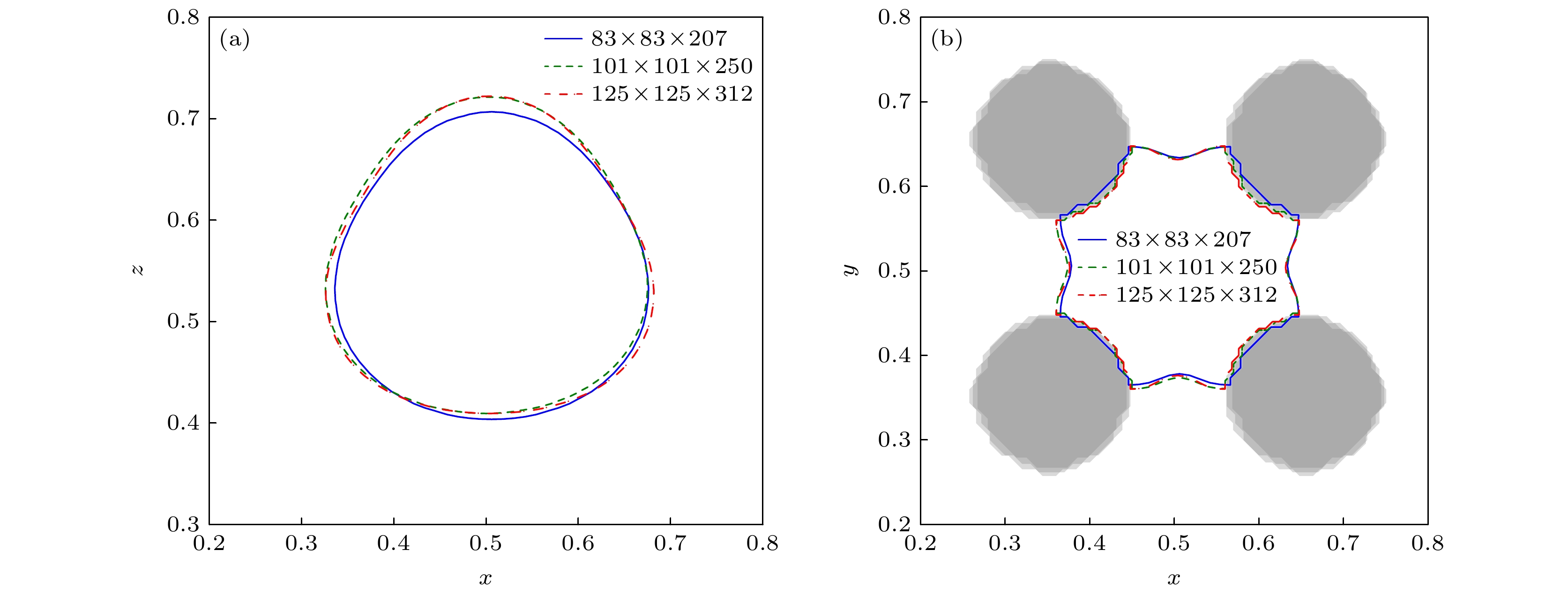
图 2 不同网格下气泡在y = Ly/2和z = h3切面上轮廓变化 (a) t* = 2.19时刻气泡在y = Ly/2切面的轮廓; (b) t* = 3.69时刻气泡在z = h3切面的的轮廓
Figure 2. The contour changes of the bubble on the y = Ly/2 and z = h3 sections under different grids: (a) The contour of the bubble on the y = Ly/2 section at t* = 2.19; (b) the contour of the bubble on the z = h3 section at t* = 3.57.
图 3 不同Eo与接触角组合下的气泡形态变化.
Figure 3. Changes in bubble morphology under different combinations of Eo numbers and contact angles.
图 4 不同工况下未通过多孔介质的气泡形态
Figure 4. The morphology of bubbles that do not pass through porous media under different working conditions.
图 5 气泡平均速度${v_{{\text{ave}}}}$在(a)不同Eo与(b)接触角θ工况下的变化趋势.
Figure 5. Variation trend of average bubble velocity under (a) different Eo numbers and (b) contact angle θ conditions.
图 6 瞬时速度v*在不同Eo下随θ的变化 (a) Eo = 10; (b) Eo = 100
Figure 6. Variation of instantaneous velocity v* with θ at different Eo numbers: (a) Eo = 10; (b) Eo = 100.
图 7 气泡在 (a)绿色圆点、(b) 蓝色方块、(c) 红色三角处的位置与形态
Figure 7. The position and shape of bubbles at (a) green dots, (b) blue squares, (c) red triangles.
图 8 气泡在(a)不同Re与(b)不同θ工况下vave的变化趋势
Figure 8. Variation trend of bubble vave under (a) different Re and (b) different θ conditions.
图 9 不同Re与接触角耦合作用下气泡的形态变化.
Figure 9. Changes in bubble morphology under the coupling effect of different Re and contact angle.
图 10 气泡在(a)不同Eo和(b)不同Re组合下vave的变化情况
Figure 10. Changes in the bubble vave under (a) different Eo numbers and (b) different Re number combinations.
图 11 不同Re与Eo耦合作用下气泡的形态变化
Figure 11. Changes in bubble morphology under the coupling of different Re and Eo numbers.
-
[1] Lichtschlag A, Haeckel M, Olierook D, Peel K, Flohr A, Pearce C R, Marieni C, James R H, Connelly D P 2021 Int. J. Greenh. Gas Control 109 103352
Google Scholar
[2] 张沐安, 王进卿, 吴睿, 冯致, 詹明秀, 徐旭, 池作和 2023 72 164701
Google Scholar
Zhang M A, Wang J Q, Wu R, Feng Z, Zhan M X, Xu X, Chi Z H 2023 Acta Phys. Sin. 72 164701
Google Scholar
[3] Ajayi T, Gomes J S, Bera A 2019 Petrol. Sci. 16 1028
Google Scholar
[4] Liu H B, Xu H, Pan L M, Zhong D H, Liu Y 2019 Int. J. Hydrogen Energy 44 22780
Google Scholar
[5] 王季康, 李华, 彭宇飞, 李晓燕, 张新宇 2022 71 158802
Google Scholar
Wang J K, Li H, Peng Y F, Li X Y, Zhang X Y 2022 Acta Phys. Sin. 71 158802
Google Scholar
[6] Zhang D, Li Y, Yuan H 2023 Desalination 566 116902
Google Scholar
[7] Haris S, Qiu X, Klammler H, Mohamed M M A 2020 Groundw. Sustain. Dev. 11 100463
Google Scholar
[8] Li Y F, Yang G Q, Yu S L, Mo J K, Li K, Xie Z Q, Ding L, Wang W T, Zhang F Y 2021 Electrochim. Acta 370 137751
Google Scholar
[9] Wang C Y, Beckermann C, Fan C 1994 Numer. Heat Transf. Part A: Appl. 26 375
Google Scholar
[10] Wang H, Lou Q, Liu G, Li L 2022 Int. J. Therm. Sci. 178 107554
Google Scholar
[11] 张森, 娄钦 2024 73 026401
Google Scholar
Zhang S, Lou Q 2024 Acta Phys. Sin. 73 026401
Google Scholar
[12] Roosevelt S E, Corapcioglu M Y 1998 Water Resour. Res. 34 1131
Google Scholar
[13] Corapcioglu M Y, Cihan A, Drazenovic M 2004 Water Resour. Res. 40 4
[14] Ma Y, Kong X Z, Scheuermann A, Galindo-Torres S A, Bringemeier D, Li L 2015 Water Resour. Res. 51 4359
Google Scholar
[15] Ghasemian S, Ahmadzadegan A, Chatzis I 2019 Transp. Porous Media 129 811
Google Scholar
[16] Liu N, Ju B, Yang Y, Brantson E T, Wang J, Tian Y 2019 J. Petrol. Sci. Eng. 180 396
Google Scholar
[17] Qian Y H, D'Humières D, Lallemand P 1992 Europhys. Lett. 17 479
Google Scholar
[18] 郭照立, 郑楚光 2009 格子Boltzmann方法的原理及应用(北京: 科学出版社) 第42页
Guo Z L, Zheng C G 2009 Theory and Applications of Lattice Boltzmann Method (Beijing: Science Press) p42
[19] Shi J, Ma Q, Chen Z 2019 Microgravity Sci. Technol. 31 207
Google Scholar
[20] Sattari E, Zanous S P, Farhadi M, Mohamad A 2020 J. Power Sources 454 227929
Google Scholar
[21] Inamuro T, Ogata T, Ogino F 2004 Future Gener. Comput. Syst. 20 959
Google Scholar
[22] Yu K, Yong Y M, Yang C 2020 Processes 8 1608
Google Scholar
[23] Fakhari A, Bolster D 2017 J. Comput. Phys. 334 620
Google Scholar
[24] Alizadeh M, Seyyedi S M, Rahni M T, Ganji D D 2017 J. Mol. Liq. 236 151
Google Scholar
[25] Chen G Q, Huang X, Zhang A M, Wang S P, Li T 2019 Phys. Fluids 31 097104
Google Scholar
[26] Zhang A, Guo Z P, Wang Q G, Xiong S M 2019 Phys. Fluids 31 063106
Google Scholar
[27] Zhang A, Su D B, Li C M, Zhang Y, Jiang B, Pan F S 2022 Phys. Fluids 34 043312
Google Scholar
[28] Gunstensen A K, Rothman D H, Zaleski S, Zanetti G 1991 Phys. Rev. A 43 4320
Google Scholar
[29] Shan X, Chen H 1993 Phys. Rev. E 47 1815
Google Scholar
[30] Shan X, Chen H 1994 Phys. Rev. E 49 2941
Google Scholar
[31] Swift M R, Osborn W R, Yeomans J M 1995 Phys. Rev. Lett. 75 830
Google Scholar
[32] Swift M R, Orlandini E, Osborn W R, Yeomans J M 1996 Phys. Rev. E 54 5041
Google Scholar
[33] He X, Luo L S 1997 Phys. Rev. E 55 6333
Google Scholar
[34] He X, Luo L S 1997 Phys. Rev. E 56 6811
Google Scholar
[35] Liang H, Xu J R, Chen J X, Wang H L, Chai Z H, Shi B C 2018 Phys. Rev. E 97 033309
Google Scholar
[36] Chiu P H, Lin Y T 2011 J. Comput. Phys. 230 185
Google Scholar
[37] Unverdi S O, Tryggvason G 1992 J. Comput. Phys. 100 25
Google Scholar
[38] Wei Y K, Li Y M, Wang Z D, Yang H, Zhu Z C, Qian Y H, Luo K H 2022 Phys. Rev. E 105 015103
Google Scholar
[39] Jeon D H, Kim S, Kim M, Lee C, Cho H S 2023 J. Power Sources 553 232322
Google Scholar
[40] Yi T H, Zhang W Y, Qiu Y N, Lei G, Yu Y Z, Wu J Y, Yang G 2023 Int. J. Multiphase Flow 169 104601
Google Scholar
[41] 娄钦, 汤升, 王浩原 2021 计算物理 38 289
Lou Q, Tang S, Wang H Y 2021 J. Comput. Phys. 38 289
DownLoad:
Metrics
- Abstract views: 374
- PDF Downloads: 5
- Cited By: 0
