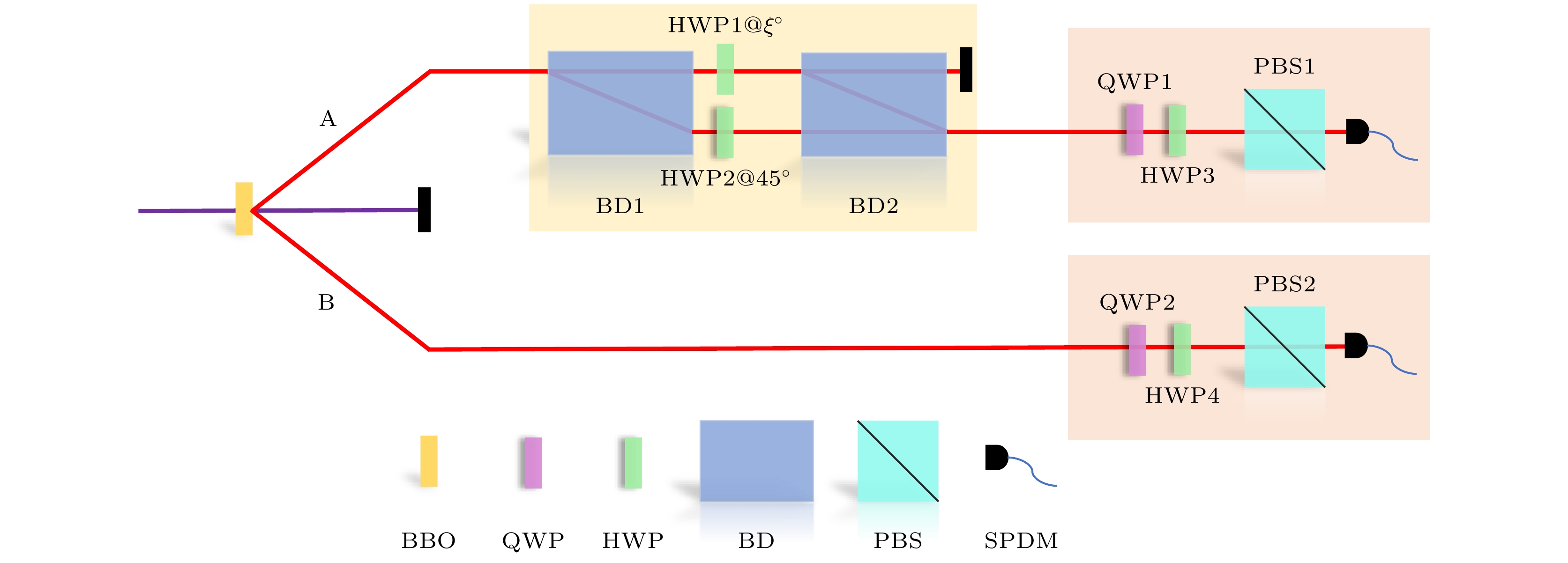
-
Quantum entanglement is a unique phenomenon of quantum mechanics and the core of many quantum technologies. Although entanglement is often observed in small-scale systems, detecting weak entanglement in large or noisy systems remains a major challenge, as experimental flaws can easily destroy fragile quantum correlations. A new weak entanglement detection criterion based on quantum steering has recently been proposed as a potential alternative to traditional entanglement witnesses. In this work, we provide a theoretical analysis by comparing the detection capabilities of the steering-based criterion with those of traditional entanglement witnesses under realistic measurement errors. The results show that the steering-based approach offers improved sensitivity for detecting weak entanglement. We further experimentally verify the feasibility of this steering-based criterion by using a linear optical setup. The experimental results align well with theoretical predictions, confirming the practicality and reliability of the method. These findings provide the steering-based criterion as a promising and accessible tool for detecting weak entanglement, and are expected to have potential applications in quantum communication, quantum computing, and other areas of quantum information science.
[1] Bell J S 1964 Physics Physique Fizika 1 195
Google Scholar
[2] Aspect A, Dalibard J, Roger G 1982 Phys. Rev. Lett. 49 1804
Google Scholar
[3] Weihs G, Jennewein T, Simon C, Weinfurter H, Zeilinger A 1998 Phys. Rev. Lett. 81 5039
Google Scholar
[4] Horodecki R, Horodecki P, Horodecki M, Horodecki K 2009 Rev. Mod. Phys. 81 865
Google Scholar
[5] Leibfried D, Knill E, Seidelin S, Britton J, Blakestad R B, Chiaverini J, Hume D B, Itano W M, Jost J D, Langer C, Ozeri R, Reichle R, Wineland D J 2005 Nature 438 639
Google Scholar
[6] Lu C Y, Zhou X Q, Gühne O, Gao W B, Zhang J, Yuan Z S, Goebel A, Yang T, Pan J W 2007 Nat. Phys. 3 91
Google Scholar
[7] Rijavec S, Carlesso M, Bassi A, Vedral V, Marletto C 2021 New J. Phys. 23 043040
Google Scholar
[8] Tilly J, Marshman R J, Mazumdar A, Bose S 2021 Phys. Rev. A 104 052416
Google Scholar
[9] Marshman R J, Mazumdar A, Bose S 2020 Phys. Rev. A 101 052110
Google Scholar
[10] Cataño-Lopez S B, Santiago-Condori J G, Edamatsu K, Matsumoto N 2020 Phys. Rev. Lett. 124 221102
Google Scholar
[11] Matsumoto N, Cataño-Lopez S B, Sugawara M, Suzuki S, Abe N, Komori K, Michimura Y, Aso Y, Edamatsu K 2019 Phys. Rev. Lett. 122 071101
Google Scholar
[12] Lambert N, Chen Y N, Cheng Y C, Li C M, Chen G Y, Nori F 2013 Nat. Phys. 9 10
Google Scholar
[13] Cao J, Cogdell R J, Coker D F, Duan H G, Hauer J, Kleinekathöfer U, Jansen T L C, Mančal T, Miller R J D, Ogilvie J P, Prokhorenko V I, Renger T, Tan H S, Tempelaar R, Thorwart M, Thyrhaug E, Westenhoff S, Zigmantas D 2020 Sci. Adv. 6 eaaz4888
Google Scholar
[14] Engel G S, Calhoun T R, Read E L, Ahn T K, Mančal T, Cheng Y C, Blankenship R E, Fleming G R 2007 Nature 446 782
Google Scholar
[15] Bose S, Mazumdar A, Morley G W, Ulbricht H, Toroš M, Paternostro M, Geraci A A, Barker P F, Kim M S, Milburn G 2017 Phys. Rev. Lett. 119 240401
Google Scholar
[16] Marletto C, Vedral V 2017 Phys. Rev. Lett. 119 240402
Google Scholar
[17] Nguyen H C, Bernards F 2020 Eur. Phys. J. D 74 69
Google Scholar
[18] Chevalier H, Paige A J, Kim M S 2020 Phys. Rev. A 102 022428
Google Scholar
[19] Miki D, Matsumura A, Yamamoto K 2021 Phys. Rev. D 103 026017
Google Scholar
[20] Feng T, Vedral V 2022 Phys. Rev. D 106 066013
Google Scholar
[21] Chen J L, Su H Y, Xu Z P, Pati A K 2016 Sci. Rep. 6 32075
Google Scholar
[22] Feng T, Ren C, Feng Q, Luo M, Qiang X, Chen J, Zhou X 2021 Photonics Res. 9 992
Google Scholar
[23] Cao H, Morelli S, Rozema L A, Zhang, C, Tavakoli A, Walther P 2024 Phys. Rev. Lett. 133 150201
Google Scholar
[24] Morelli S, Yamasaki H, Huber M, Tavakoli A 2022 Phys. Rev. Lett. 128 250501
Google Scholar
[25] Shih Y H, Sergienko A V 1994 Phys. Rev. A 50 2564
Google Scholar
[26] Kwiat P G, Waks E, White A G, Appelbaum I, Eberhard P H 1999 Phys. Rev. A 60 R773
Google Scholar
-
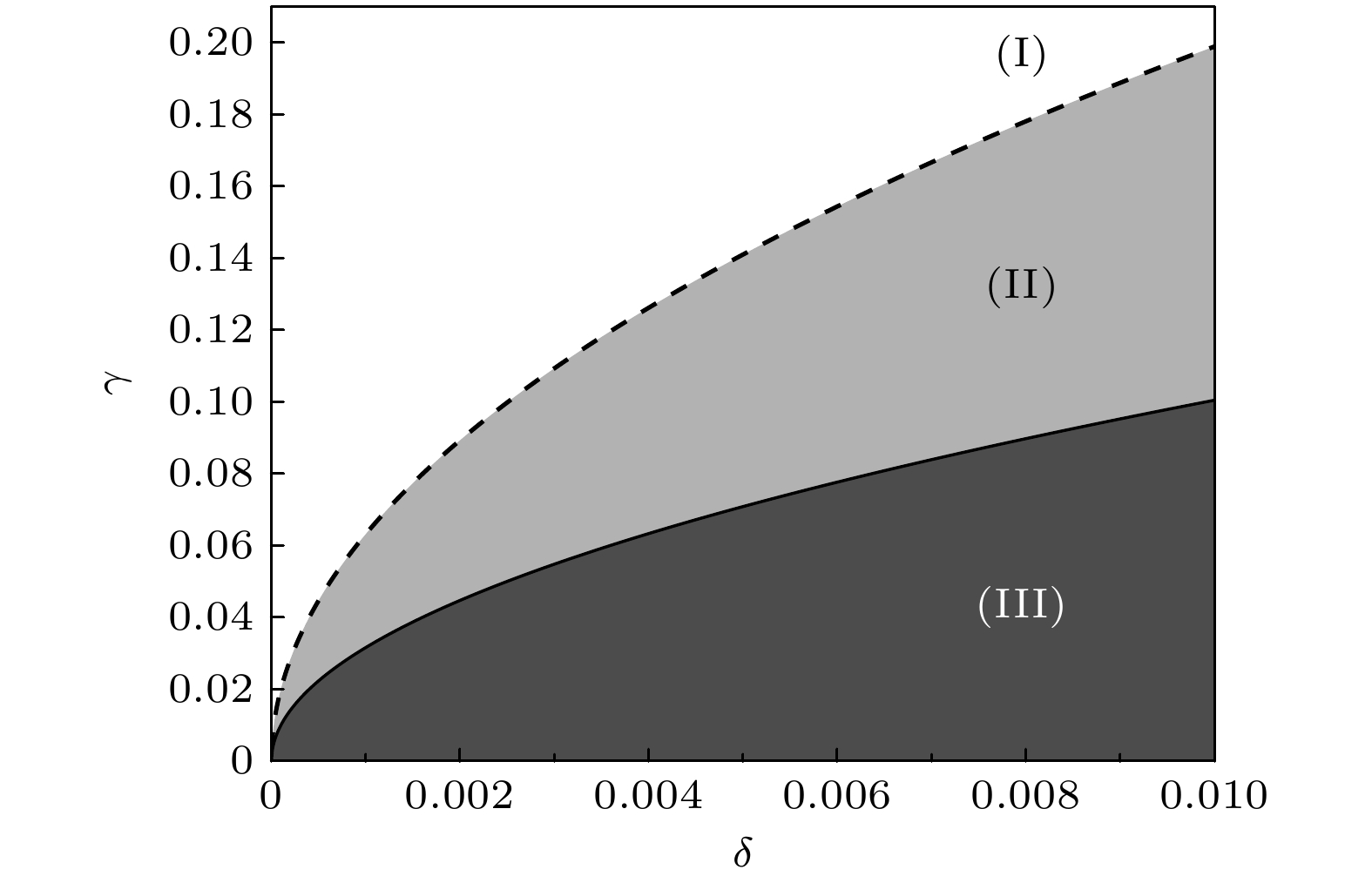
图 1 基于量子导引与基于纠缠目击者的量子纠缠判据比较. (I)为基于量子导引和基于纠缠目击者两种判据都可以检测到量子纠缠的区域; (II)为基于量子导引判据可以检测到量子纠缠的区域, 此区域基于纠缠目击者判据无法检测出量子纠缠; (III)为两种判据都无法检测出量子纠缠的区域. $ \gamma $为纠缠程度参数, $ \delta $为测量精度参数
Figure 1. Comparison of quantum entanglement criteria based on quantum steering and entanglement witnesses. (I) Represents the region where both quantum steering-based and entanglement witness-based criteria can detect quantum entanglement; (II) denotes the region where entanglement can be detected by the quantum steering-based criterion but not by the entanglement witness-based criterion; (III) indicates the region where neither criterion can detect quantum entanglement. $ \gamma $ is the entanglement strength parameter, and $ \delta $ is the measurement precision parameter.
图 2 两光子非对称纠缠态制备与测量装置示意图
Figure 2. Schematic diagram of the experimental setup for preparing and measuring asymmetric entangled two-photon states
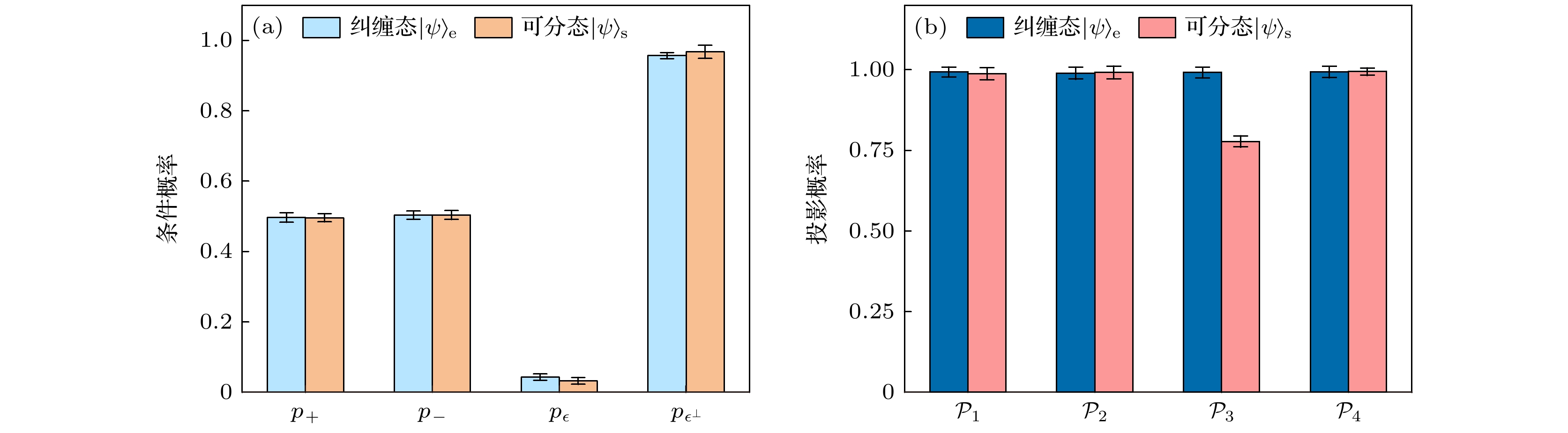
图 3 $ \varepsilon $设定为$ {9\pi}/{20} $时的实验结果 (a)在基矢$ {|+\rangle, |-\rangle} $和$ {|\varepsilon\rangle, \left|\varepsilon^{\perp}\right\rangle} $下, 对光子A进行测量, 得到4个条件概率$ p_+, $$ \; p_-,\; p_{\varepsilon},\; p_{\varepsilon^{\perp}} $. 浅蓝色柱对应纠缠态$ |\psi\rangle_{\mathrm{e}} $的条件概率, 橙色柱对应可分态$ |\psi\rangle_{\mathrm{s}} $的条件概率; (b)在测量光子A后, 光子B投影到指定量子态下的投影概率为$ \{{\cal{P}} _1, {\cal{P}} _2, {\cal{P}} _3, {\cal{P}} _4\} $. 深蓝色柱对应纠缠态$ |\psi\rangle_{\mathrm{e}} $的投影概率, 粉色柱对应$ |\psi\rangle_{\mathrm{s }}$的投影概率
Figure 3. The experimental results when $\varepsilon $ is set to $ {9\pi}/{20} $. (a) Photon A was measured in the bases $ {|+\rangle, |-\rangle} $ and $ {|\varepsilon\rangle, \left|\varepsilon^{\perp}\right\rangle} $, producing four conditional probabilities: $ p_+,\; p_-,\; p_{\varepsilon}, \;p_{\varepsilon^{\perp}} $. Light blue bars correspond to the conditional probabilities of the entangled state $ |\psi\rangle_{\mathrm{e}} $, while orange bars represent those of the separable state $ |\psi\rangle_{\mathrm{s}} $. (b) After the measurement of photon A, photon B was projected onto specific quantum states, resulting in projection probabilities $ \{{\cal{P}} _1, {\cal{P}} _2, {\cal{P}} _3, {\cal{P}} _4\} $. Dark blue bars illustrate the projection probabilities for the entangled state $ |\psi\rangle_{\mathrm{e}} $, while pink bars denote those for the separable state $ |\psi\rangle_{\mathrm{s}} $.
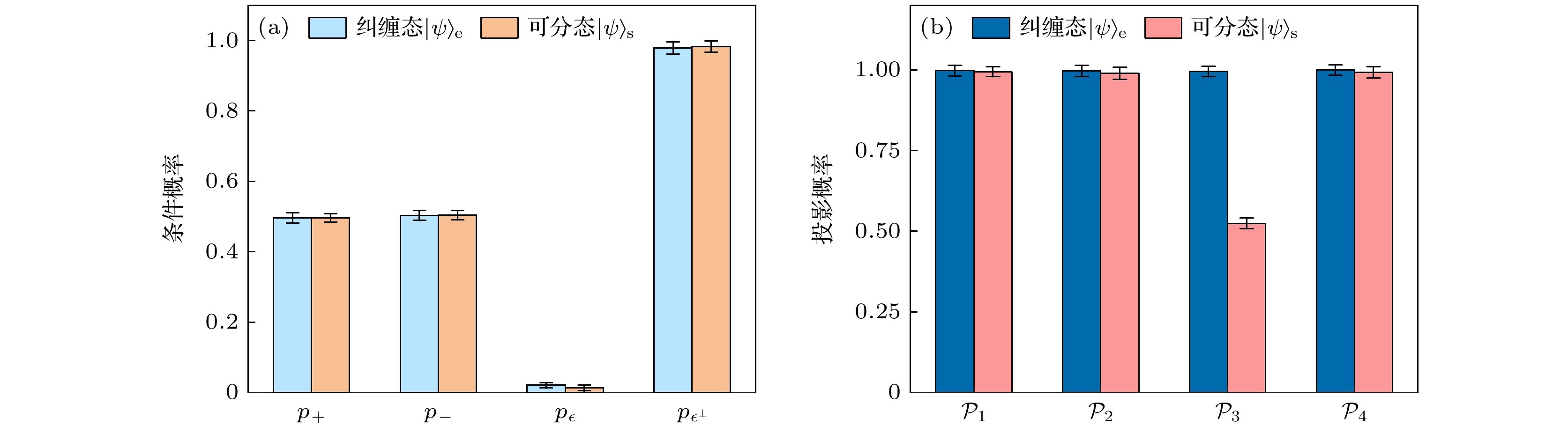
图 4 $ \varepsilon $设定为$ {17\pi}/{36} $时的实验结果 (a)在基矢$ {|+\rangle, |-\rangle} $和$ {|\varepsilon\rangle, \left|\varepsilon^{\perp}\right\rangle} $下, 对光子A进行测量, 得到4个条件概率$ p_+, $$ p_-,\; p_{\varepsilon},\; p_{\varepsilon^{\perp}} $. 浅蓝色柱对应纠缠态$ |\psi\rangle_{\mathrm{e}} $的条件概率, 橙色柱对应可分态$ |\psi\rangle_{\mathrm{s}} $的条件概率; (b)在测量光子A后, 对光子B投影到指定量子态下的投影概率为$ \{{\cal{P}} _1, {\cal{P}} _2, {\cal{P}} _3, {\cal{P}} _4\} $. 深蓝色柱对应纠缠态$ |\psi\rangle_{\mathrm{e}} $的投影概率, 粉色柱对应$ |\psi\rangle_{\mathrm{s}} $的投影概率
Figure 4. The experimental results when $\varepsilon $ is set to $ {17\pi}/{36} $: (a) Photon A was measured in the bases $ {|+\rangle, |-\rangle} $ and $ {|\varepsilon\rangle, \left|\varepsilon^{\perp}\right\rangle} $, producing four conditional probabilities: $ p_+,\; p_-,\; p_{\varepsilon},\; p_{\varepsilon^{\perp}} $. Light blue bars correspond to the conditional probabilities of the entangled state $ |\psi\rangle_e $, while orange bars represent those of the separable state $ |\psi\rangle_{\mathrm{s}} $. (b) After the measurement of photon A, photon B is projected onto specific quantum states, resulting in projection probabilities $ \{{\cal{P}} _1, {\cal{P}} _2, {\cal{P}} _3, {\cal{P}} _4\} $. Dark blue bars illustrate the projection probabilities for the entangled state $ |\psi\rangle_{\mathrm{e }}$, while pink bars denote those for the separable state $ |\psi\rangle_{\mathrm{s}} $.
-
[1] Bell J S 1964 Physics Physique Fizika 1 195
Google Scholar
[2] Aspect A, Dalibard J, Roger G 1982 Phys. Rev. Lett. 49 1804
Google Scholar
[3] Weihs G, Jennewein T, Simon C, Weinfurter H, Zeilinger A 1998 Phys. Rev. Lett. 81 5039
Google Scholar
[4] Horodecki R, Horodecki P, Horodecki M, Horodecki K 2009 Rev. Mod. Phys. 81 865
Google Scholar
[5] Leibfried D, Knill E, Seidelin S, Britton J, Blakestad R B, Chiaverini J, Hume D B, Itano W M, Jost J D, Langer C, Ozeri R, Reichle R, Wineland D J 2005 Nature 438 639
Google Scholar
[6] Lu C Y, Zhou X Q, Gühne O, Gao W B, Zhang J, Yuan Z S, Goebel A, Yang T, Pan J W 2007 Nat. Phys. 3 91
Google Scholar
[7] Rijavec S, Carlesso M, Bassi A, Vedral V, Marletto C 2021 New J. Phys. 23 043040
Google Scholar
[8] Tilly J, Marshman R J, Mazumdar A, Bose S 2021 Phys. Rev. A 104 052416
Google Scholar
[9] Marshman R J, Mazumdar A, Bose S 2020 Phys. Rev. A 101 052110
Google Scholar
[10] Cataño-Lopez S B, Santiago-Condori J G, Edamatsu K, Matsumoto N 2020 Phys. Rev. Lett. 124 221102
Google Scholar
[11] Matsumoto N, Cataño-Lopez S B, Sugawara M, Suzuki S, Abe N, Komori K, Michimura Y, Aso Y, Edamatsu K 2019 Phys. Rev. Lett. 122 071101
Google Scholar
[12] Lambert N, Chen Y N, Cheng Y C, Li C M, Chen G Y, Nori F 2013 Nat. Phys. 9 10
Google Scholar
[13] Cao J, Cogdell R J, Coker D F, Duan H G, Hauer J, Kleinekathöfer U, Jansen T L C, Mančal T, Miller R J D, Ogilvie J P, Prokhorenko V I, Renger T, Tan H S, Tempelaar R, Thorwart M, Thyrhaug E, Westenhoff S, Zigmantas D 2020 Sci. Adv. 6 eaaz4888
Google Scholar
[14] Engel G S, Calhoun T R, Read E L, Ahn T K, Mančal T, Cheng Y C, Blankenship R E, Fleming G R 2007 Nature 446 782
Google Scholar
[15] Bose S, Mazumdar A, Morley G W, Ulbricht H, Toroš M, Paternostro M, Geraci A A, Barker P F, Kim M S, Milburn G 2017 Phys. Rev. Lett. 119 240401
Google Scholar
[16] Marletto C, Vedral V 2017 Phys. Rev. Lett. 119 240402
Google Scholar
[17] Nguyen H C, Bernards F 2020 Eur. Phys. J. D 74 69
Google Scholar
[18] Chevalier H, Paige A J, Kim M S 2020 Phys. Rev. A 102 022428
Google Scholar
[19] Miki D, Matsumura A, Yamamoto K 2021 Phys. Rev. D 103 026017
Google Scholar
[20] Feng T, Vedral V 2022 Phys. Rev. D 106 066013
Google Scholar
[21] Chen J L, Su H Y, Xu Z P, Pati A K 2016 Sci. Rep. 6 32075
Google Scholar
[22] Feng T, Ren C, Feng Q, Luo M, Qiang X, Chen J, Zhou X 2021 Photonics Res. 9 992
Google Scholar
[23] Cao H, Morelli S, Rozema L A, Zhang, C, Tavakoli A, Walther P 2024 Phys. Rev. Lett. 133 150201
Google Scholar
[24] Morelli S, Yamasaki H, Huber M, Tavakoli A 2022 Phys. Rev. Lett. 128 250501
Google Scholar
[25] Shih Y H, Sergienko A V 1994 Phys. Rev. A 50 2564
Google Scholar
[26] Kwiat P G, Waks E, White A G, Appelbaum I, Eberhard P H 1999 Phys. Rev. A 60 R773
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 367
- PDF Downloads: 10
- Cited By: 0
