-
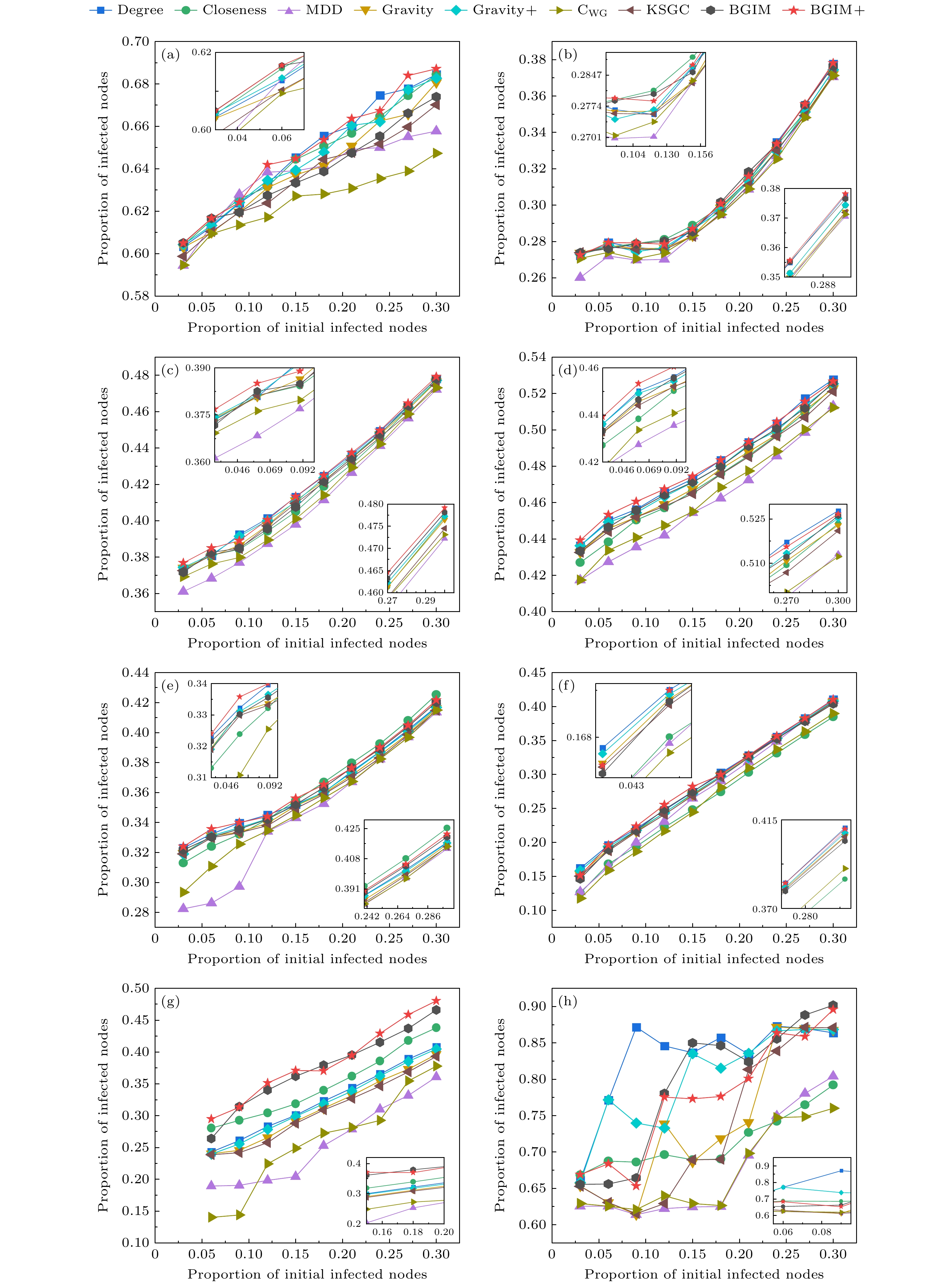
In complex networks, the accurate assessing of node importance is essential for understanding critical structures and optimizing dynamic processes. Traditional gravity-based methods often rely on local attributes or global shortest paths, which exhibit limitations in heterogeneous networks due to insufficient differentiation of node roles and their influences in different topologies. To address these challenges, we propose the bi-dimensional gravity influence model (BGIM) and its enhanced version (BGIM+). These models introduce a novel entropy-weighted gravity framework that integrates node information entropy, gravity correction factors, and asymmetric attraction factors. By replacing degree centrality with information entropy, BGIM captures nodes’ uncertainty and information richness, offering a more comprehensive view of their potential influence. The gravity correction factor (NGCF) combines eigenvector centrality with network constraint coefficients to balance global feature and local feature, while the asymmetric attraction factor (AAF) consider gravitational asymmetry between core and peripheral nodes. This bi-dimensional method can evaluate the node importance in more detail and solve the problem of imbalanced influence distribution in different network structures. A normalization mechanism further enhances adaptability, thus ensuring robust performance in both sparse and dense networks. Extensive experiments on real-world (e.g., Jazz, USAir, Email, Router) and synthetic (LFR-generated) networks validate the proposed models. The results demonstrate that BGIM and BGIM+ consistently outperform classical methods (such as Degree, Closeness, and Betweenness centralities) in identifying critical nodes and predicting their roles in propagation dynamics. In particular, BGIM+ exhibits superior performance in networks with complex topology, achieving high correlation with SIR (Susceptible-Infected-Recovered) model simulations under different propagation rates. Moreover, BGIM+ effectively balances the influences of local hubs and global bridges, thus it is particularly suitable for heterogeneous networks. This study highlights the significance of incorporating multidimensional features into gravity models for accurate and robust node evaluation. The proposed model advances the development of complex network analysis by providing a universal tool for identifying influential nodes indifferent applications, including epidemic control, information dissemination, and infrastructure resilience. The applicability of BGIM in temporal and dynamic network contexts will be explored in future, so as to further expand its application scope. -
Keywords:
- complex networks /
- information entropy /
- gravity model /
- multidimensional features
[1] Li H J, Xu W Z, Song S P, Wang W X, Perc M 2021 Chaos, Solitons Fractals 151 111294
 Google Scholar
Google Scholar
[2] Freeman L C 1978 Soc. Networks 1 215
 Google Scholar
Google Scholar
[3] Freeman L C 1977 Sociometry 40 35
 Google Scholar
Google Scholar
[4] Bonacich P, Lloyd P 2001 Soc. Networks 23 191
 Google Scholar
Google Scholar
[5] Sabidussi G 1966 Psychometrika 31 581
 Google Scholar
Google Scholar
[6] Kitsak M, Gallos L K, Havlin S, Liljeros F, Muchnik L, Stanley H E, Makse H A 2010 Nat. Phys. 6 888
 Google Scholar
Google Scholar
[7] Bae J, Kim S 2014 Physica A 395 549
 Google Scholar
Google Scholar
[8] Zeng A, Zhang C J 2013 Phys. Lett. A 377 1031
 Google Scholar
Google Scholar
[9] Liu Y, Tang M, Zhou T, Do Y 2015 Sci. Rep. 5 13172
 Google Scholar
Google Scholar
[10] Ma L L, Ma C, Zhang H F, Wang B H 2016 Physica A 451 205
 Google Scholar
Google Scholar
[11] Li Z, Huang X 2021 Sci. Rep. 11 21249
 Google Scholar
Google Scholar
[12] Liu F, Wang Z, Deng Y 2020 Knowl. Based Syst. 193 105464
 Google Scholar
Google Scholar
[13] Zhao J, Wen T, Jahanshahi H, Cheong K H 2022 Inf. Sci. 609 1706
 Google Scholar
Google Scholar
[14] Yang X, Xiao F 2021 Knowl. Based Syst. 227 107198
 Google Scholar
Google Scholar
[15] Yu Y, Zhou B, Chen L, Gao T, Liu J 2022 Entropy. 24 275
 Google Scholar
Google Scholar
[16] Jaoude A A 2017 Syst. Sci. Control. Eng. 5 380
 Google Scholar
Google Scholar
[17] Hu J, Wang B, Lee D 2010 IEEE/ACM Int'l Conference on Green Computing and Communications & Int'l Conference on Cyber, Physical and Social Computing Hangzhou, China, March 7, 2011 p792
[18] Chiranjeevi M, Dhuli V S, Enduri M K, Cenkeramaddi L R 2023 IEEE Access 11 126195
 Google Scholar
Google Scholar
[19] Wang J, Li C, Yi X C 2018 Appl. Math. Comput. 334 388
 Google Scholar
Google Scholar
[20] 阮逸润, 老松杨, 汤俊, 白亮, 郭延明 2022 71 176401
 Google Scholar
Google Scholar
Ruan Y R, Lao S Y, Tang J, Bai L, Guo Y M 2022 Acta Phys. Sin. 71 176401
 Google Scholar
Google Scholar
[21] Lü L Y, Zhou T, Zhang Q M, Stanley H E 2016 Nat. Commun. 7 10168
 Google Scholar
Google Scholar
[22] Burt R S, Kilduff M, Tasselli S 2013 Annu. Rev. Psychol. 64 527
 Google Scholar
Google Scholar
[23] 韩忠明, 吴杨, 谭旭升, 段大高, 杨伟杰 2015 64 020101
 Google Scholar
Google Scholar
Han Z M, Wu Y, Tan X S, Duan D G, Yang W J 2015 Acta Phys.Sin. 64 020101
 Google Scholar
Google Scholar
[24] Brin S, Page L 1998 Comput. Netw. ISDN Syst. 30 107
 Google Scholar
Google Scholar
[25] Cao Z, Qin T, Liu T Y, Tsai M F, Hang L 2007 ICML '07: Proceedings of the 24th International Conference on Machine Learning Corvalis, USA, June 20–24, 2007 p129
[26] Liang F C, Lu Y 2021 IEEE Sixth International Conference on Data Science in Cyberspace (DSC) Shenzhen, China, October 9–11, 2021 p602
[27] Rodrigues F A 2018 arXiv:1901.07901 [physics.soc-ph]
[28] Pastor-Satorras R, Vespignani A 2001 Phys. Rev. Lett. 86 3200
 Google Scholar
Google Scholar
[29] Hethcote H W 2000 SIAM Rev. 42 599
 Google Scholar
Google Scholar
[30] Moreno Y, Pastor-Satorras R, Vespignani A 2002 Eur. Phys. J. B 26 521
 Google Scholar
Google Scholar
[31] Kendall M G 1938 Biometrika 30 81
 Google Scholar
Google Scholar
-
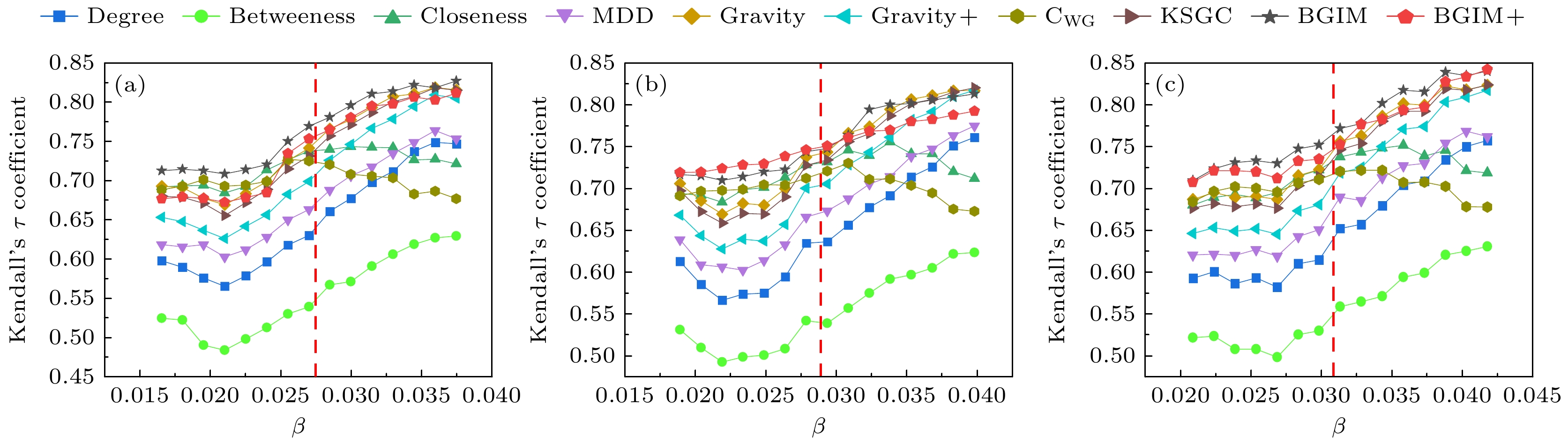
图 5 LFR人工合成网络上各评估方法的Kendall系数 (a) $ \langle k \rangle = 5 $; (b) $ \langle k \rangle = 10 $; (c) $ \langle k \rangle = 20 $
Figure 5. The Kendall coefficients for various evaluation methods on LFR synthetic networks: (a) $ \langle k \rangle = 5 $; (b) $ \langle k \rangle = 10 $; (c) $ \langle k \rangle = 20 $.
表 1 8个常见网络的基本拓扑特征统计
Table 1. Basic topological features of the eight real networks.
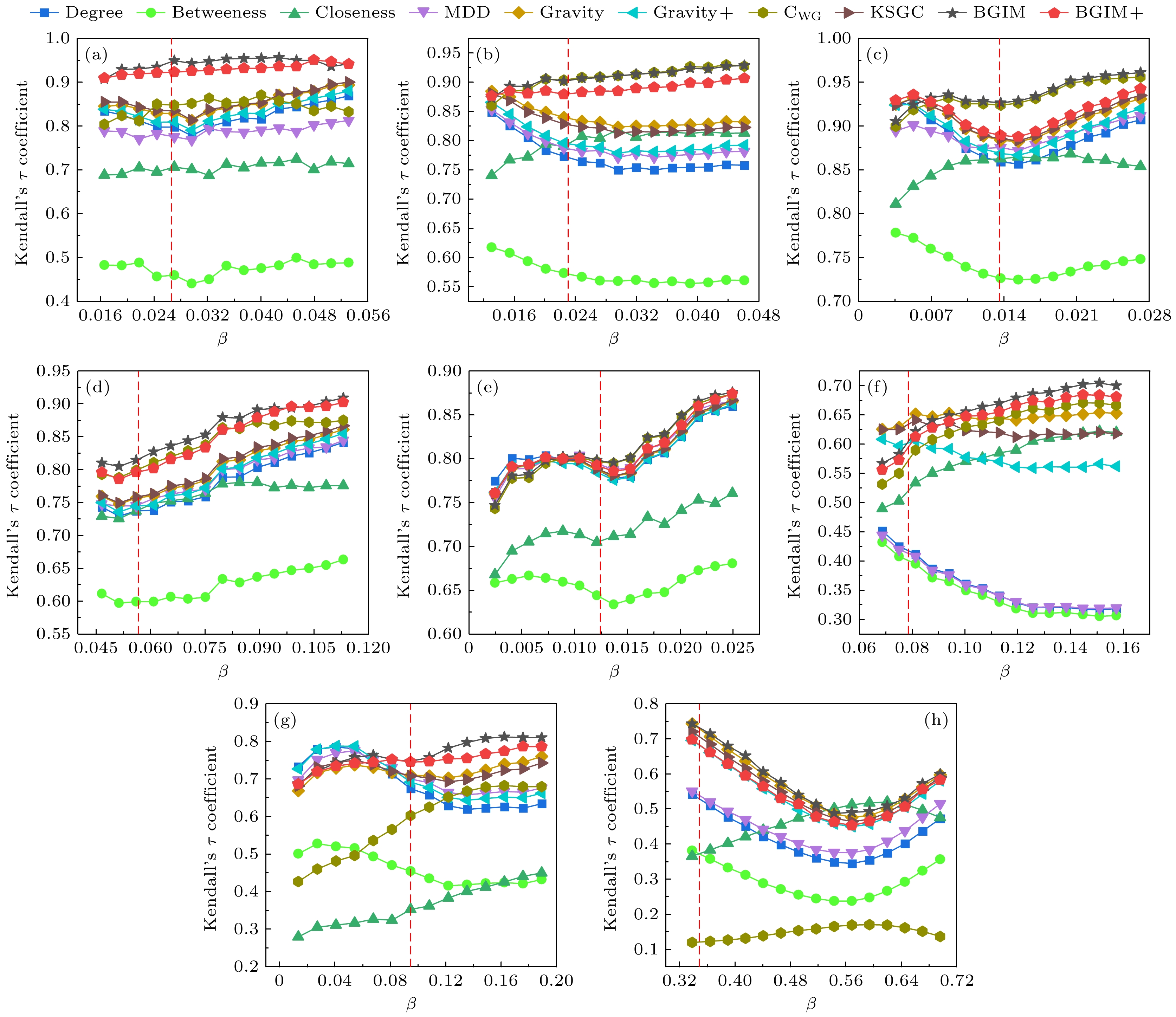
Network N E $ \langle d \rangle $ c $ \langle k \rangle $ $ ks_{{\rm{max}}} $ $ \beta_{{\rm{th}}} $ $ \beta_{\rm{c}} $ Jazz 198 2742 2.2350 0.6157 27.6969 29 0.0266 0.0547 USAir 332 2126 2.7381 0.6252 12.8072 26 0.0231 0.0487 EEC 986 16064 2.5869 0.4505 32.5842 34 0.0134 0.0191 Email 1133 5451 3.6060 0.2201 9.6222 11 0.0565 0.1187 PB 1222 16714 2.7375 0.3600 27.3552 36 0.0123 0.0246 Router 5022 6258 6.4488 0.0116 2.4922 7 0.0786 0.1266 Facebook 4039 88234 3.6925 0.6055 43.6910 115 0.0094 0.0164 Power 4941 6594 18.9892 0.0801 2.6691 5 0.3483 0.6016 表 2 各个引力模型在小规模网络中所得到部分节点的排名信息
Table 2. Ranking information of some nodes obtained by various gravity models across seven networks.
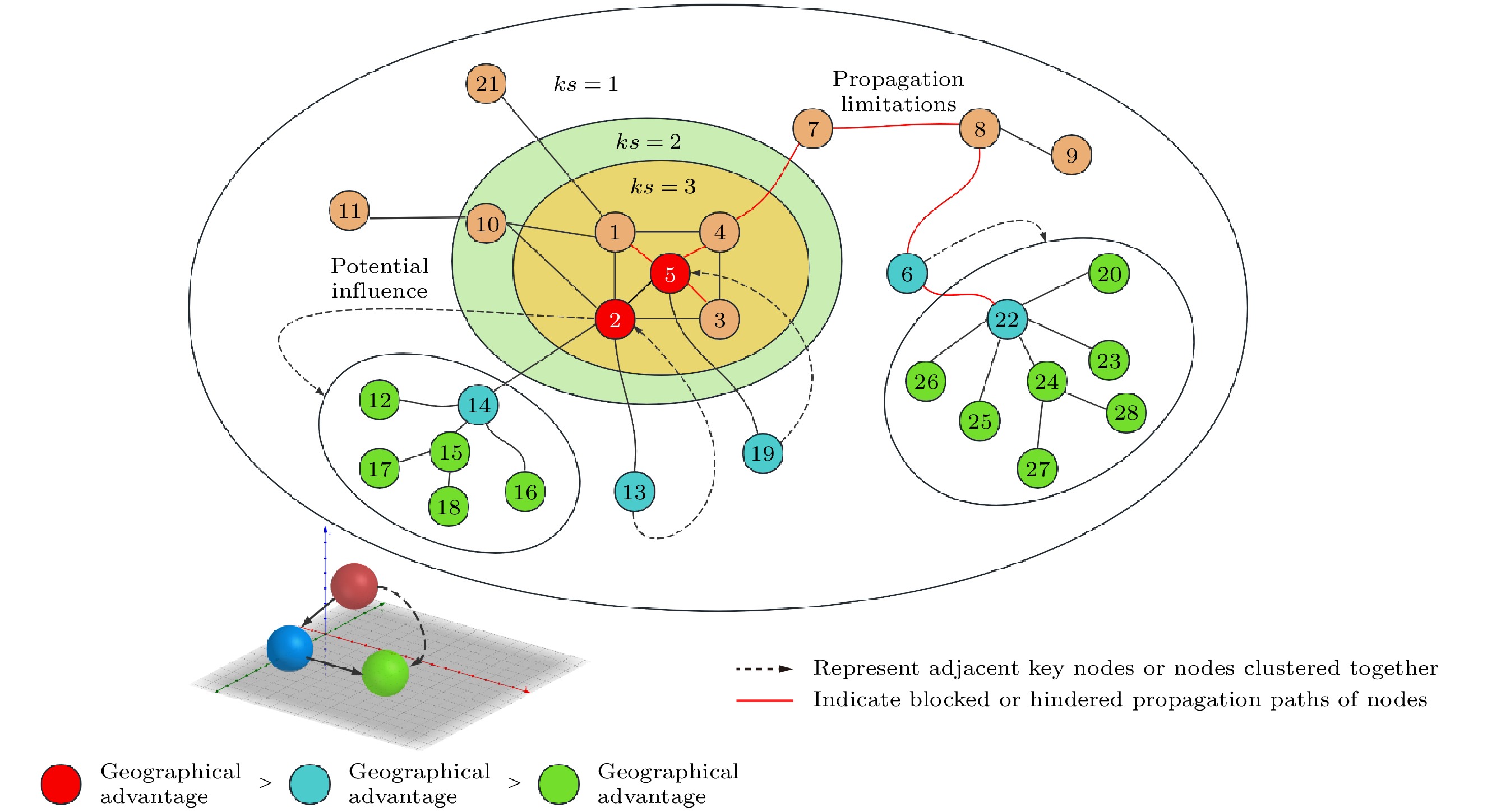
Rank Gravity Gravity+ KSGC CWG BGIM BGIM+ SIR 1 14 22 3 3 14 3 14 2 22 14 22 14 3 14 6 3 3 3 14 7 6 6 3 4 7 7 6 22 22 7 22 5 6 6 7 6 7 22 7 表 3 各个引力模型在七个网络中的区分度表现
Table 3. Differentiation performance of various gravity models across seven networks.
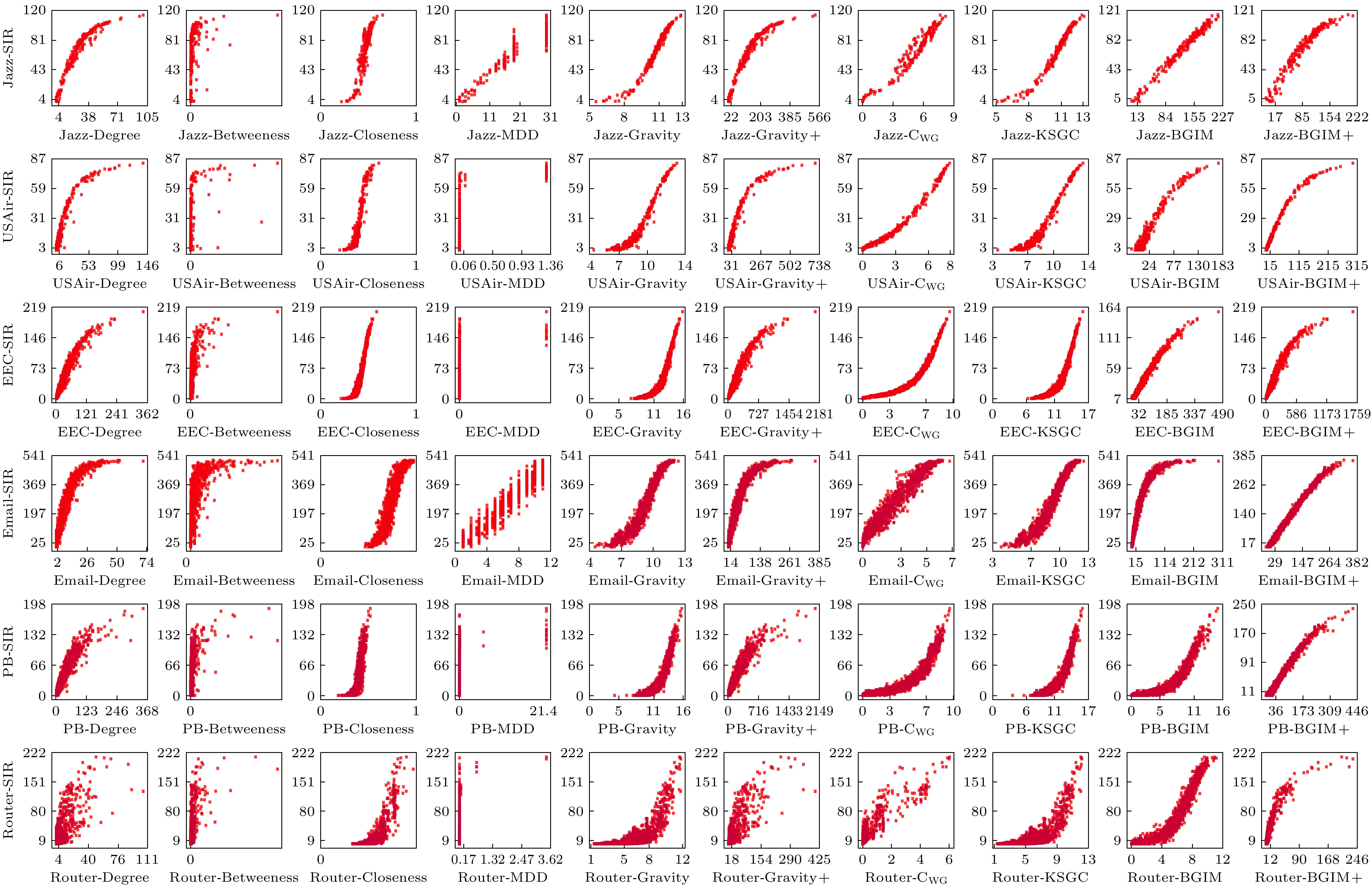
网络名 Gravity Gravity+ KSGC CWG BGIM BGIM+ Jazz 0.999282 0.999487 0.999282 0.999692 0.999742 0.999351 USAir 0.995092 0.995092 0.995092 0.999199 0.999663 0.996145 EEC 0.999868 0.999868 0.999868 0.999975 0.999993 0.999841 Email 0.999891 0.999897 0.999897 0.999997 0.999983 0.999912 PB 0.999279 0.999279 0.999279 0.999912 0.999981 0.999279 Router 0.996384 0.996447 0.996452 0.998819 0.998819 0.997221 Facebook 0.999866 0.999886 0.999874 0.999999 0.999998 0.999915 Power 0.999884 0.999889 0.999888 0.815190 0.999998 0.978472 -
[1] Li H J, Xu W Z, Song S P, Wang W X, Perc M 2021 Chaos, Solitons Fractals 151 111294
 Google Scholar
Google Scholar
[2] Freeman L C 1978 Soc. Networks 1 215
 Google Scholar
Google Scholar
[3] Freeman L C 1977 Sociometry 40 35
 Google Scholar
Google Scholar
[4] Bonacich P, Lloyd P 2001 Soc. Networks 23 191
 Google Scholar
Google Scholar
[5] Sabidussi G 1966 Psychometrika 31 581
 Google Scholar
Google Scholar
[6] Kitsak M, Gallos L K, Havlin S, Liljeros F, Muchnik L, Stanley H E, Makse H A 2010 Nat. Phys. 6 888
 Google Scholar
Google Scholar
[7] Bae J, Kim S 2014 Physica A 395 549
 Google Scholar
Google Scholar
[8] Zeng A, Zhang C J 2013 Phys. Lett. A 377 1031
 Google Scholar
Google Scholar
[9] Liu Y, Tang M, Zhou T, Do Y 2015 Sci. Rep. 5 13172
 Google Scholar
Google Scholar
[10] Ma L L, Ma C, Zhang H F, Wang B H 2016 Physica A 451 205
 Google Scholar
Google Scholar
[11] Li Z, Huang X 2021 Sci. Rep. 11 21249
 Google Scholar
Google Scholar
[12] Liu F, Wang Z, Deng Y 2020 Knowl. Based Syst. 193 105464
 Google Scholar
Google Scholar
[13] Zhao J, Wen T, Jahanshahi H, Cheong K H 2022 Inf. Sci. 609 1706
 Google Scholar
Google Scholar
[14] Yang X, Xiao F 2021 Knowl. Based Syst. 227 107198
 Google Scholar
Google Scholar
[15] Yu Y, Zhou B, Chen L, Gao T, Liu J 2022 Entropy. 24 275
 Google Scholar
Google Scholar
[16] Jaoude A A 2017 Syst. Sci. Control. Eng. 5 380
 Google Scholar
Google Scholar
[17] Hu J, Wang B, Lee D 2010 IEEE/ACM Int'l Conference on Green Computing and Communications & Int'l Conference on Cyber, Physical and Social Computing Hangzhou, China, March 7, 2011 p792
[18] Chiranjeevi M, Dhuli V S, Enduri M K, Cenkeramaddi L R 2023 IEEE Access 11 126195
 Google Scholar
Google Scholar
[19] Wang J, Li C, Yi X C 2018 Appl. Math. Comput. 334 388
 Google Scholar
Google Scholar
[20] 阮逸润, 老松杨, 汤俊, 白亮, 郭延明 2022 71 176401
 Google Scholar
Google Scholar
Ruan Y R, Lao S Y, Tang J, Bai L, Guo Y M 2022 Acta Phys. Sin. 71 176401
 Google Scholar
Google Scholar
[21] Lü L Y, Zhou T, Zhang Q M, Stanley H E 2016 Nat. Commun. 7 10168
 Google Scholar
Google Scholar
[22] Burt R S, Kilduff M, Tasselli S 2013 Annu. Rev. Psychol. 64 527
 Google Scholar
Google Scholar
[23] 韩忠明, 吴杨, 谭旭升, 段大高, 杨伟杰 2015 64 020101
 Google Scholar
Google Scholar
Han Z M, Wu Y, Tan X S, Duan D G, Yang W J 2015 Acta Phys.Sin. 64 020101
 Google Scholar
Google Scholar
[24] Brin S, Page L 1998 Comput. Netw. ISDN Syst. 30 107
 Google Scholar
Google Scholar
[25] Cao Z, Qin T, Liu T Y, Tsai M F, Hang L 2007 ICML '07: Proceedings of the 24th International Conference on Machine Learning Corvalis, USA, June 20–24, 2007 p129
[26] Liang F C, Lu Y 2021 IEEE Sixth International Conference on Data Science in Cyberspace (DSC) Shenzhen, China, October 9–11, 2021 p602
[27] Rodrigues F A 2018 arXiv:1901.07901 [physics.soc-ph]
[28] Pastor-Satorras R, Vespignani A 2001 Phys. Rev. Lett. 86 3200
 Google Scholar
Google Scholar
[29] Hethcote H W 2000 SIAM Rev. 42 599
 Google Scholar
Google Scholar
[30] Moreno Y, Pastor-Satorras R, Vespignani A 2002 Eur. Phys. J. B 26 521
 Google Scholar
Google Scholar
[31] Kendall M G 1938 Biometrika 30 81
 Google Scholar
Google Scholar
Catalog
Metrics
- Abstract views: 2949
- PDF Downloads: 62
- Cited By: 0














 DownLoad:
DownLoad: