Simulation study on the azimuthal evolution of electrons from high-altitude nuclear explosions based on CIMI model

LUO Zhekai; SUN Qiang; XIE Lun; PU Zuyin; ZONG Qiugang; LIU Ying; ZHOU Qianhong; FU Suiyan

doi:10.7498/aps.74.20241259

Abstract

High-altitude nuclear explosions can inject large amounts of relativistic electrons into the inner magnetosphere, resulting in the formation of artificial radiation belts. These high-energy electrons pose a potential threat to spacecraft due to their long-term stability and influence on space weather. The investigation of the formation and evolution of artificial radiation belts is of great significance for the safety of spacecraft and human space activities. In this study, the comprehensive inner magnetosphere-ionosphere (CIMI) model is used to simulate the transition of electrons from a locally concentrated distribution to an azimuthally uniform distribution, which reveals the spiral encircling, azimuthal expansion, and diffusion behaviors exhibited by the electron cloud during the formation of artificial radiation belts. The CIMI model is a four-dimensional model based on the Fokker-Planck equation. It simulates the evolution of particles across four degrees of freedom: radial, azimuthal, energy, and equatorial pitch angle. Unlike previous studies that mainly focus on the long-term evolution of artificial radiation belts already reaching azimuthal uniformity, this work specifically ascertains the azimuthal evolution process of the injected electrons and how they form the artificial radiation belts. Numerical simulations are conducted on the captured nuclear explosion electrons initially concentrated at L = 1.1–2.2 and covering approximately one time zone azimuthally. The results show that the injected electrons primarily evolve into an azimuthally uniform distribution through a spiral encircling process, with diffusion playing a smaller role. In this process, the electrons undergo eastward drift, with those at higher altitudes exhibiting faster drift velocities. The velocity shear leads to the formation of a helical structure around the Earth. Additionally, the formation of this spiral structure is accompanied by azimuthal expansion, driven mainly by energy and pitch angle dispersion during the drift. Electrons with different energy values and equatorial pitch angles exhibit varying drift speeds, contributing to the azimuthal expansion of electron clusters during the drift. The expansion process can fill the gaps in the helical structure. Ultimately, the electron distribution achieves azimuthal uniformity through energy-pitch angle diffusion.

Keywords:

Authors and contacts

1.
School of Earth and Space Sciences, Peking University, Beijing 100871, China
2.
Institute Applied Physics and Computational Mathematics, Beijing 100094, China

Corresponding author: ZHOU Qianhong, zhou_qianhong@qq.com ; FU Suiyan, suiyanfu@pku.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 12375246, 12305288, 41731068).

FullText HTML

References

[1]	Lyons L R 1973 J. Geophys. Res. 78 6793 Google Scholar
[2]	Zheng Y, Ganushkina N Y, Jiggens P, Jun I, Meier M, Minow J I, O’Brien T P, Pitchford D, Shprits Y, Tobiska W K, Xapsos M A, Guild T B, Mazur J E, Kuznetsova M M 2019 Space Weather 17 1384 Google Scholar
[3]	Christofilos N C 1959 J. Geophys. Res. 64 869 Google Scholar
[4]	Beall D S, Bostrom C O, Williams D J 1967 J. Geophys. Res. 72 3403 Google Scholar
[5]	王建国, 刘利, 牛胜利, 左应红, 高银军, 朱金辉, 张相华, 李桠, 李夏至 2023 现代应用物理 14 3 Google Scholar Wang J G, Liu L, Niu S L, Zuo Y H, Gao Y J, Zhu J H, Zhang X H, Li Y, Li X Z 2023 Modern Appl. Phys. 14 3 Google Scholar
[6]	朱金辉, 左应红, 刘利, 牛胜利, 商鹏, 李夏至, 王学栋 2023 现代应用物理 14 44 Google Scholar Zhu J H, Zuo Y H, Liu L, Niu S L, Shang P, Li X Z, Wang X D 2023 Modern Appl. Phys. 14 44 Google Scholar
[7]	顾旭东, 赵正予, 倪彬彬, 汪枫 2009 58 5871 Google Scholar Gu X D, Zhao Z Y, Ni B B, Wang F 2009 Acta Phys. Sin 58 5871 Google Scholar
[8]	Tu W, Cunningham G S, Chen Y, Morley S K, Reeves G D, Blake J B, Baker D N, Spence H 2014 Geophys. Res. Lett. 41 1359 Google Scholar
[9]	Fok M C, Buzulukova N Y, Chen S H, Glocer A, Nagai T, Valek P, Perez J D 2014 J. Geophys. Res. Space Phys. 119 7522 Google Scholar
[10]	Fok M C, Wolf R A, Spiro R W, Moore T E 2001 J. Geophys. Res. Space Phys. 106 8417 Google Scholar
[11]	Fok M C, Kang S B, Ferradas C P, Buzulukova N Y, Glocer A, Komar C M 2021 J. Geophys. Res. Space Phys. 126 e2020JA028987 Google Scholar
[12]	Albert J M 2005 J. Geophys. Res. Space Phys. 110 A03218 Google Scholar
[13]	Albert J M 2008 J. Geophys. Res. Space Phys. 113 A06208 Google Scholar
[14]	Albert J M, Meredith N P, Horne R B 2009 J. Geophys. Res. Space Phys. 114 1DD Google Scholar
[15]	Weimer D R 2001 J. Geophys. Res. Space Phys. 106 407 Google Scholar
[16]	Tsyganenko N A 2012 J. Geophys. Res. Space Phys. 100 5599 Google Scholar
[17]	Tsyganenko N A, Stern D P 1996 J. Geophys. Res. Space Phys. 101 27187 Google Scholar
[18]	Tsyganenko N A, Mukai T 2003 J. Geophys. Res. Space Phys. 108 1136 Google Scholar
[19]	Tsyganenko N A, Sitnov M I 2005 J. Geophys. Res. Space Phys. 110 A03208 Google Scholar
[20]	Meredith N P, Horne R B, Thorne R M, Summers D, Anderson R R 2004 J. Geophys. Res. Space Phys. 109 A06209 Google Scholar
[21]	Meredith N P, Horne R B, Sicard-Piet A, Boscher D, Yearby K H, Li W, Thorne R M 2012 J. Geophys. Res. Space Phys. 117 A10225 Google Scholar
[22]	Rairden R L, Frank L A, Craven J D 2012 J. Geophys. Res. Space Phys. 91 13613 Google Scholar
[23]	Gombosi T I, Baker D N, Balogh A, Erickson P J, Huba J D, Lanzerotti L J 2017 Space Sci. Rev. 212 985 Google Scholar
[24]	Cowee M, Winske D 2012 Update on the Electron Source Model (Los Alamos National Laboratory) DOI: 10.2172/1046529
[25]	Dyal P 2006 J. Geophys. Res. Space Phys. 111 A12211 Google Scholar
[26]	Wang J G, Niu S L, Zhang D H 2010 The Parameter Manual Book of High-Altitude Nuclear Evplosion Effect (Beijing: Atomic Energy Press) pp259–260 [王建国, 牛胜利, 张殿辉 2010 高空核爆炸效应参数手册 (北京: 原子能出版社) 第259—260页] Wang J G, Niu S L, Zhang D H 2010 The Parameter Manual Book of High-Altitude Nuclear Evplosion Effect (Beijing: Atomic Energy Press) pp259–260
[27]	Vette J I 1991 The AE-8 Trapped Electron Model Environment Report Number: NSSDC/WDC-A-RS-91-24
[28]	Hamlin D A, Karplus R, Vik R C, Watson K M 1961 J. Geophys. Res. 66 1 Google Scholar
[29]	Southwood D J, Kivelson M G 1981 J. Geophys. Res. Space Phys. 86 5643 Google Scholar
[30]	Southwood D J, Kivelson M G 1982 J. Geophys. Res. Space Phys. 87 1707 Google Scholar
[31]	Fei Y, Chan A A, Elkington S R, Wiltberger M J 2006 J. Geophys. Res. Space Phys. 111 A12209 Google Scholar
[32]	Lejosne S, Albert J M 2023 Frontiers in Astronomy and Space Sciences 10 1200485 Google Scholar
[33]	Lejosne S, Albert J M, Walton S D 2023 Frontiers in Astronomy and Space Sciences 10 1232512 Google Scholar
[34]	Sandhu J K, Rae I J, Wygant J R, Breneman A W, Tian S, Watt C E J, Horne R B, Ozeke L G, Georgiou M, Walach M T 2021 J. Geophys. Res. Space Phys. 126 e2020JA029024 Google Scholar
[35]	Aryan H, Bortnik J, Meredith N P, Horne R B, Sibeck D G, Balikhin M A 2020 J. Geophys. Res. Space Phys. 126 e2020JA028403 Google Scholar
[36]	Malaspina D M, Zhu H, Drozdov A Y 2020 J. Geophys. Res. Space Phys. 125 e2019JA027415 Google Scholar

Cited By

图 1 注入电子的初始分布　(a)初始注入电子在不同L值上的总通量分布; (b)初始注入电子中不同能量的占比

Figure 1. Initial distribution of the injected electrons: (a) Total flux distribution of initially injected electrons at different L values; (b) proportions of different energies of the initially injected electrons

DownLoad: Full-Size Img PowerPoint

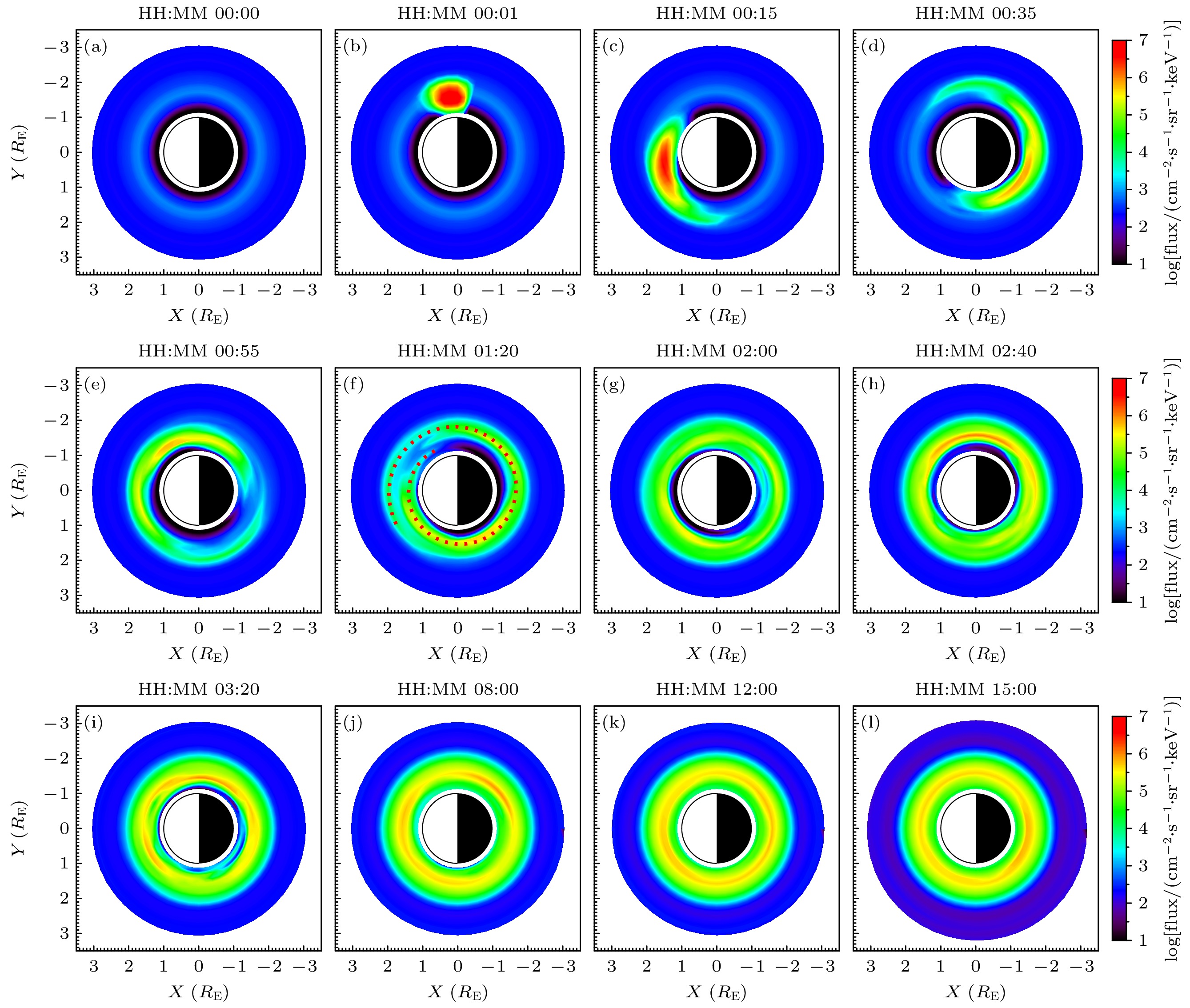
图 2 0.761 MeV电子通量的空间分布随时间的演化过程　(a)—(l)不同时刻电子微分通量在赤道面上的分布, 图中XY平面为从地球北侧看向磁赤道面的俯视图, 太阳位于图片左侧; 图(f)中红色虚线表示注入电子在漂移过程中形成的螺旋线结构

Figure 2. Temporal evolution of the spatial distribution of 0.761 MeV electrons’ flux: (a)–(l) The differential flux distribution of electrons in the equatorial plane at different times. The XY plane in the figures represents a top-down view of the magnetic equatorial plane from the Earth’s northern side, with the Sun located to the left side. The red dashed line in panel (f) indicates the spiral structure formed by the injected electrons during their drift process.

DownLoad: Full-Size Img PowerPoint

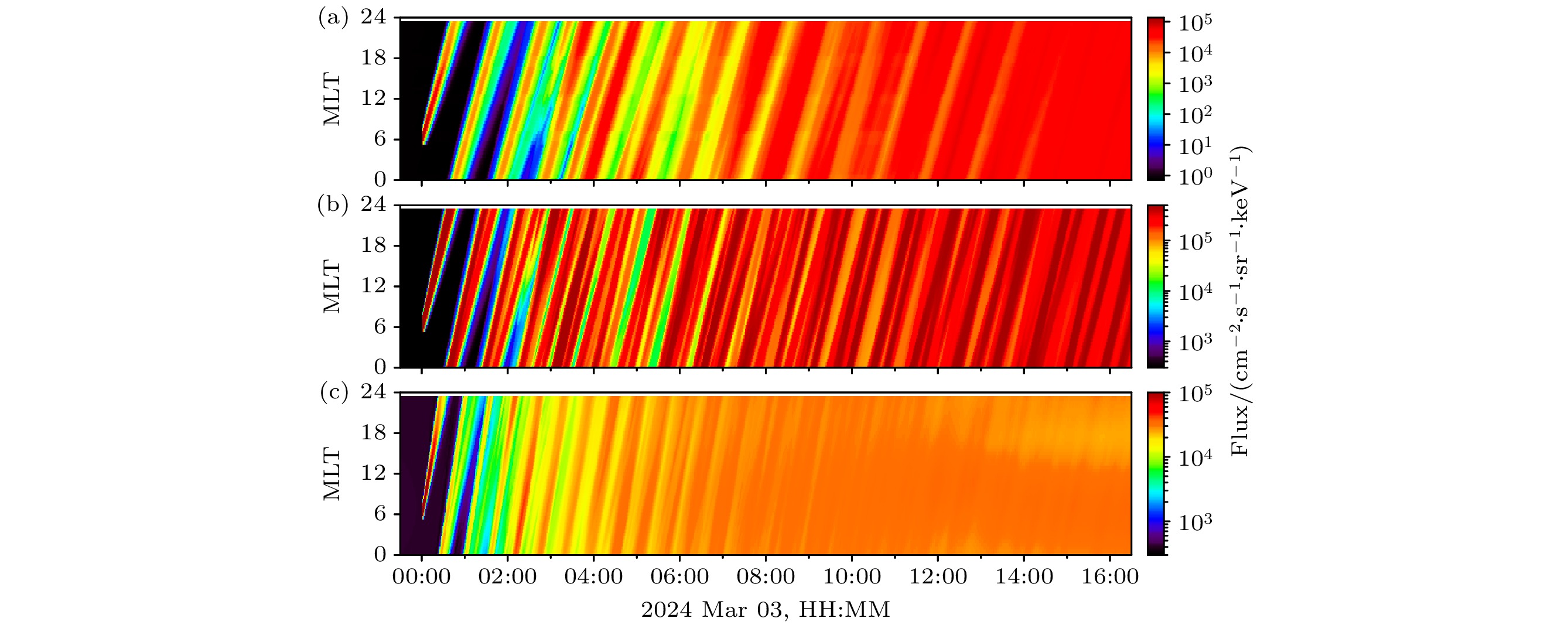
图 3 不同L处电子通量的MLT分布随时间的演化规律, 其中(a)—(c)依次为$ L=1.23 $, $ L=1.45 $, $ L=1.98 $处$ 0.761\;\rm MeV $电子的通量环向分布

Figure 3. Temporal evolution of the MLT distribution of electron flux at different L values. Panel (a)–(c) show the azimuthal distribution of 0.761 MeV electron flux at $ L=1.23 $, $ L=1.45 $, and $ L=1.98 $, respectively.

DownLoad: Full-Size Img PowerPoint

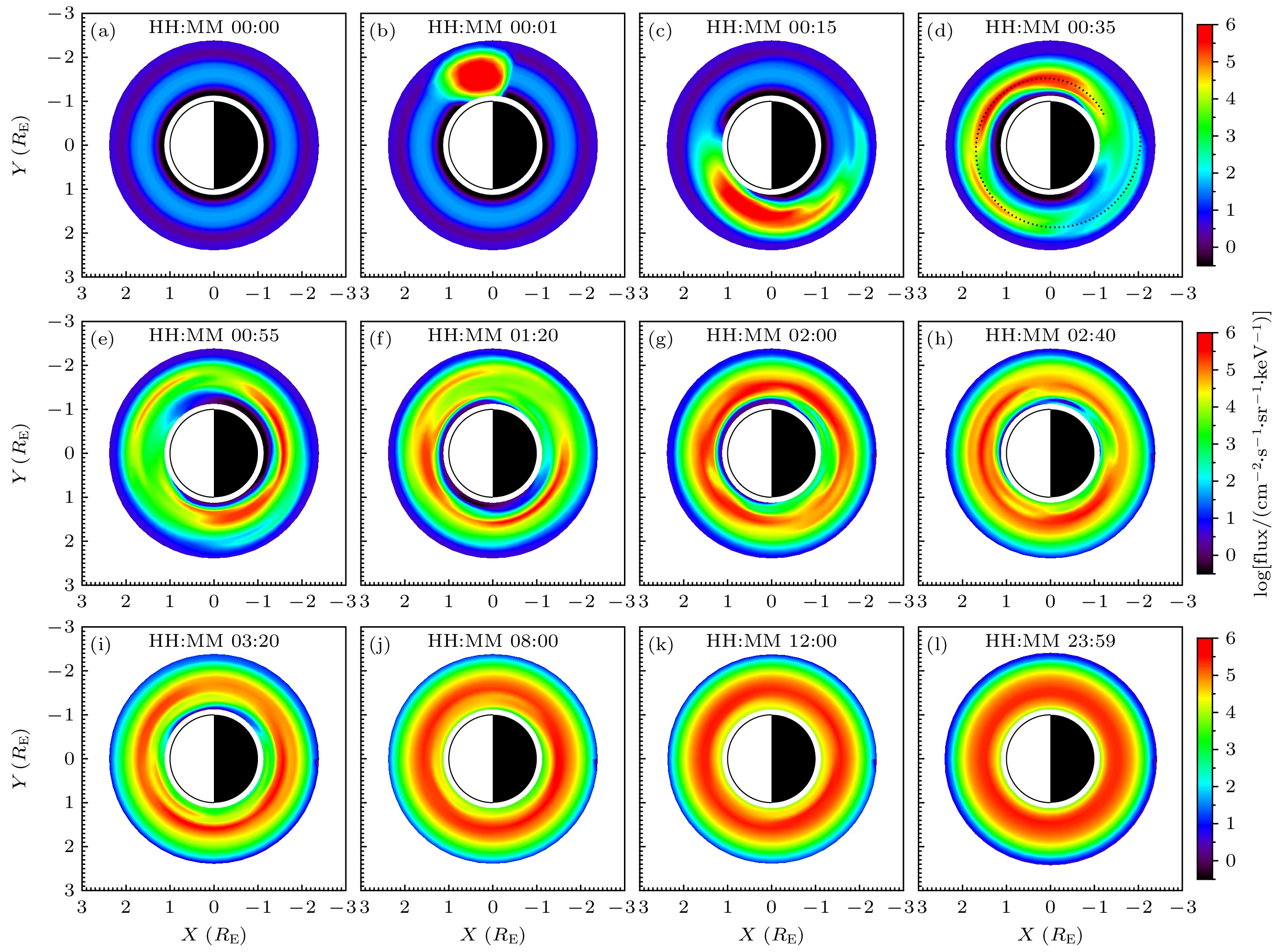
图 4 $ 1.323\;\rm MeV $电子通量的空间分布随时间的演化过程, 其中(a)—(l)为不同时刻电子微分通量在赤道面上的分布; 图(d)中黑色虚线表示注入电子在漂移过程中形成的螺旋线结构

Figure 4. Temporal evolution of the spatial distribution of 1.323 MeV electrons’ flux. Panel (a)–(l) show the differential flux distribution of electrons in the equatorial plane at different times. The black dashed line in panel (d) indicates the spiral structure formed by the injected electrons during their drift process.

DownLoad: Full-Size Img PowerPoint

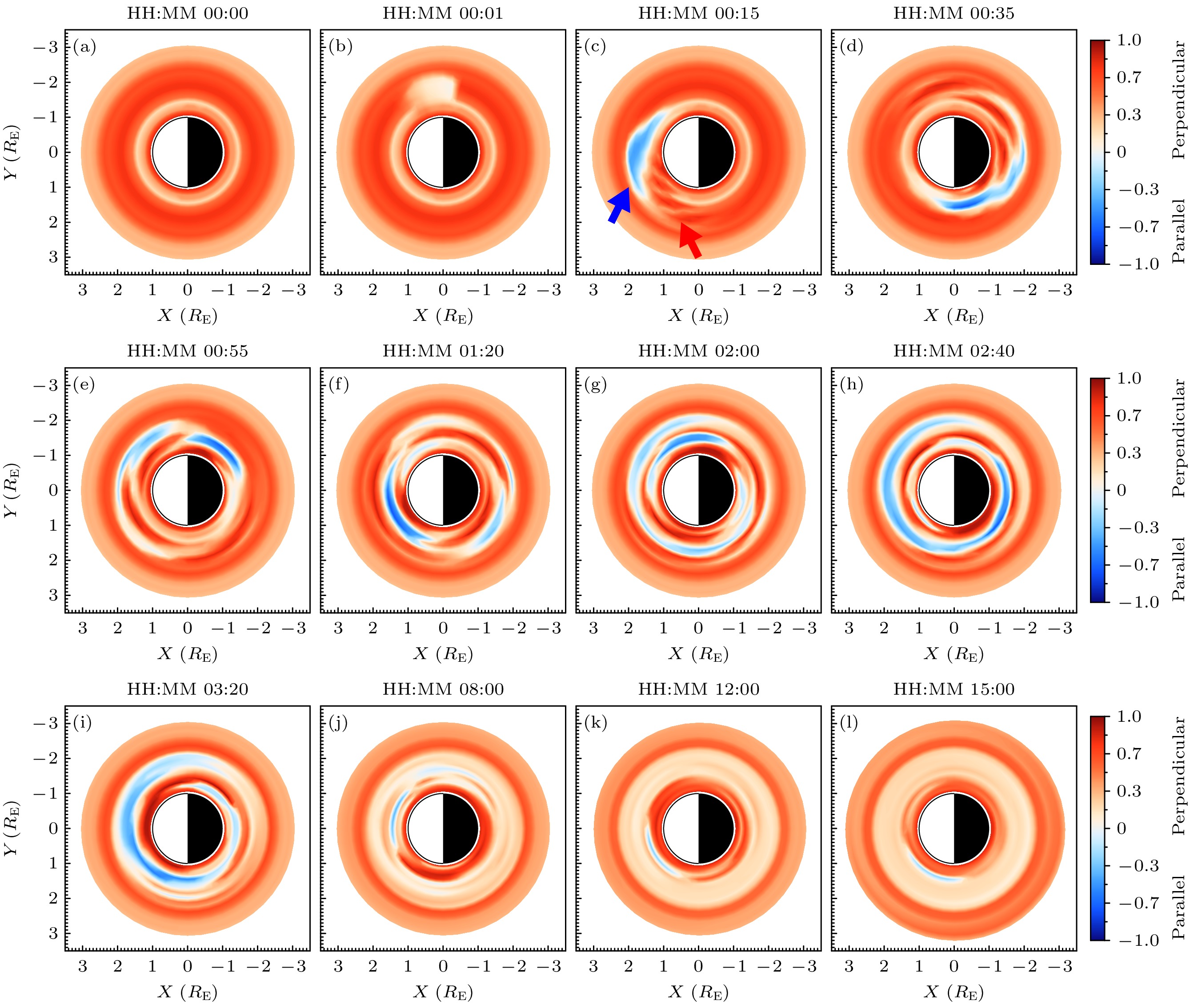
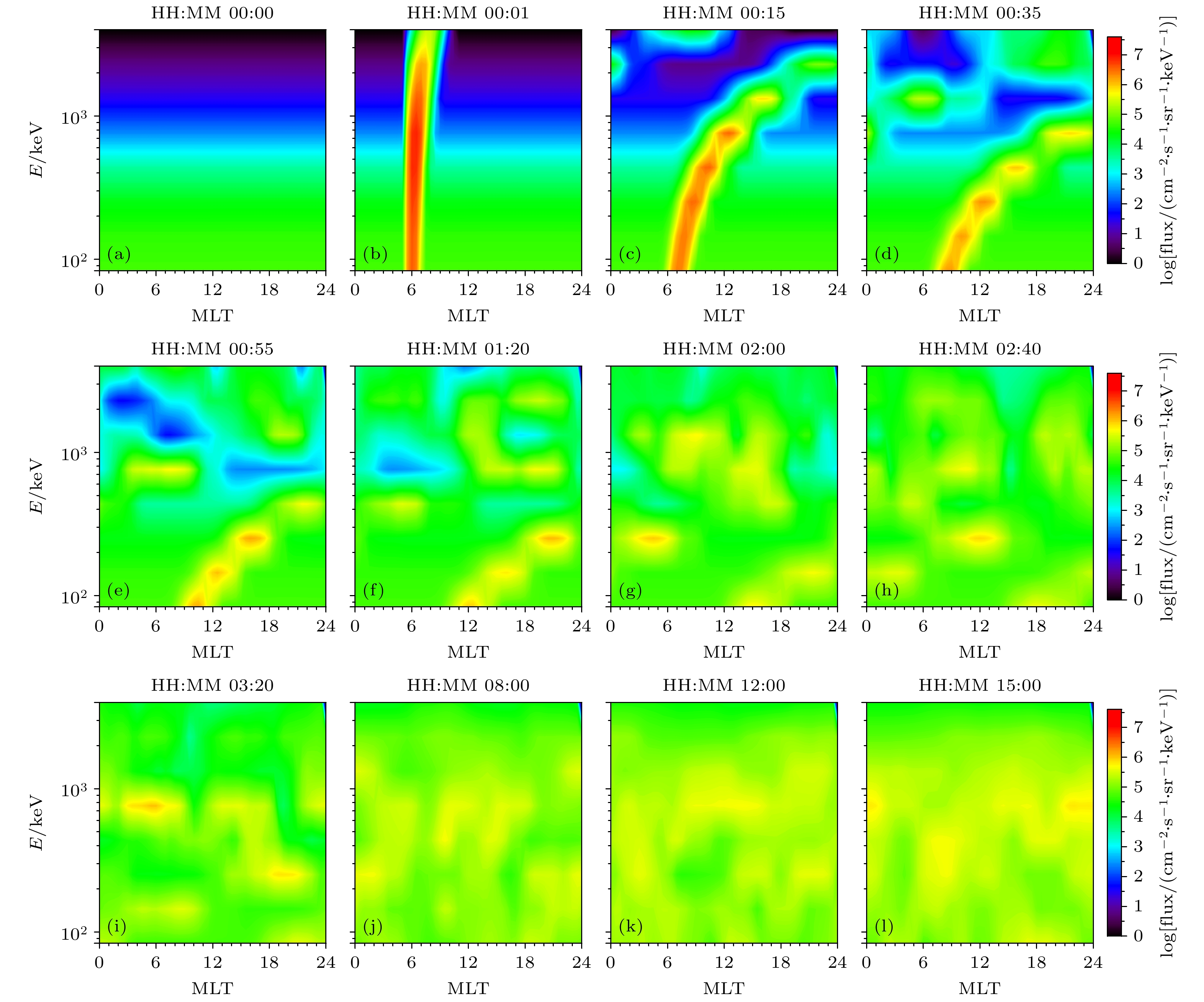
图 5 $ 0.761\;\rm MeV $电子各向异性指数的空间分布随时间的演化过程, 其中(a)—(l)分别为不同时刻电子各向异性指数在磁赤道面中的分布; 图(c)中红色箭头指示注入电子团前端各向异性指数升高的区域, 蓝色箭头指示后端各向异性指数降低的区域

Figure 5. Temporal evolution of the spatial distribution of the anisotropy index for 0.761 MeV electrons. Panel (a)–(l) show the distribution of the anisotropy index in the magnetic equatorial plane at different times. In panel (c), the red arrow indicates the region where the anisotropy index increases at the front of the injected electron cluster, while the blue arrow indicates the region where the anisotropy index decreases at the rear.

DownLoad: Full-Size Img PowerPoint

图 6 $ L=1.45 $处电子的能量-MLT分布随时间的演化过程, 其中(a)—(l)分别为不同时刻电子通量在能量-MLT空间中的分布

Figure 6. Temporal evolution of the energy-MLT distribution of electrons at $ L=1.45 $. Panel (a)–(l) show the electron flux distribution in the energy-MLT space at different times.

DownLoad: Full-Size Img PowerPoint

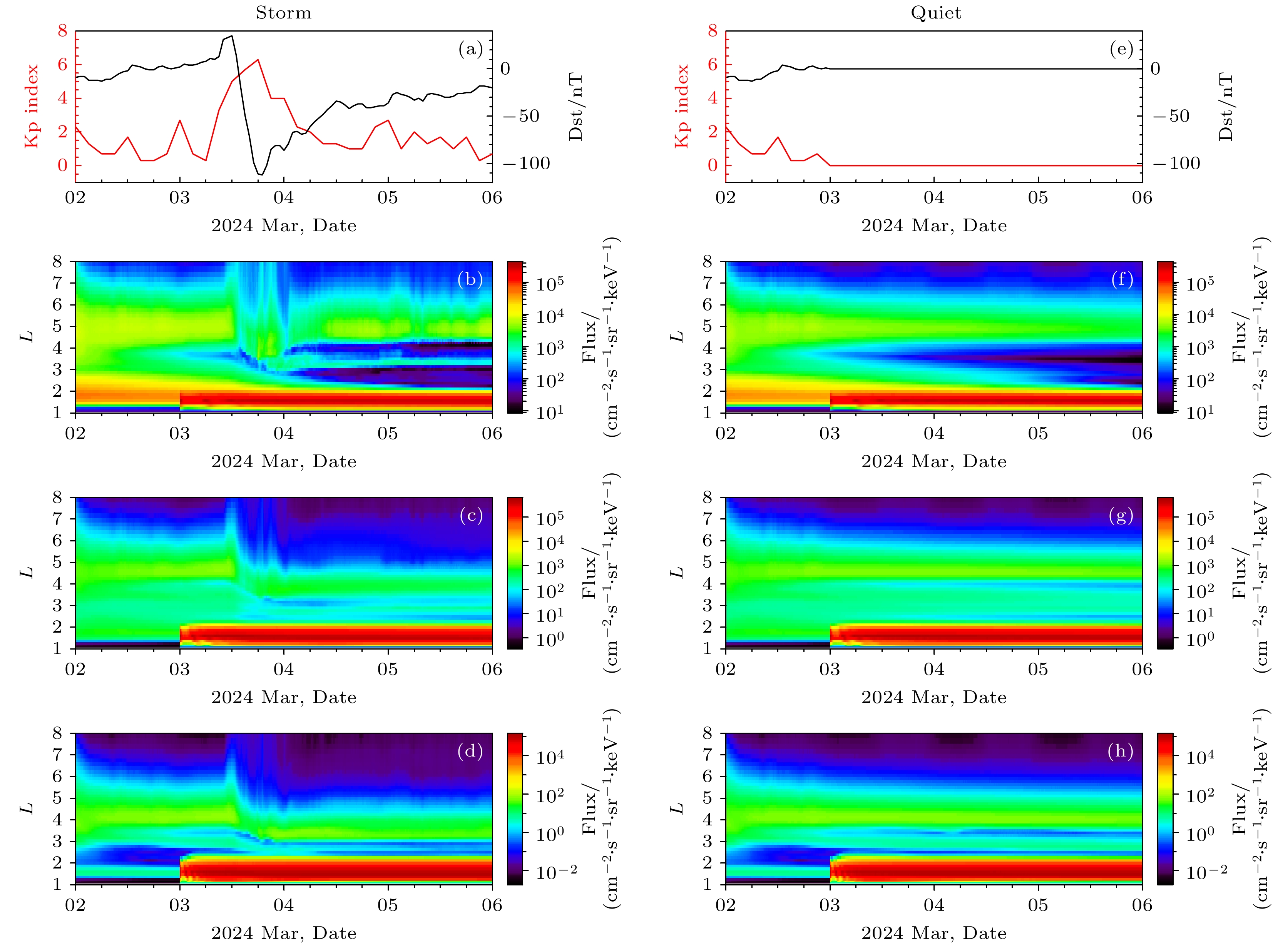
图 7 人工辐射带的长时间演化过程　(a)模拟期间的地磁指数, 红线表示Kp指数, 黑线表示Dst指数; (b)—(d) $ 0.252\;\rm MeV $, $ 0.761\;\rm MeV $, $ 2.301\;\rm MeV $电子通量的L分布随时间的演化过程, 图中通量为对应L上的环向平均通量; (e)—(h)地磁平静条件下左图相应内容

Figure 7. Long-term evolution of the artificial radiation belt: (a) The geomagnetic indices during the simulation period, with the red line representing the Kp index and the black line representing the Dst index; (b)–(d) the temporal evolution of the L distribution of electron flux for $ 0.252\;\rm MeV $, $ 0.761\;\rm MeV $, and $ 2.301\;\rm MeV $, respectively, where the flux represents the azimuthally averaged flux at the corresponding L; (e)–(h) the corresponding content under geomagnetically quiet conditions.

DownLoad: Full-Size Img PowerPoint

map

[1]	Lyons L R 1973 J. Geophys. Res. 78 6793 Google Scholar
[2]	Zheng Y, Ganushkina N Y, Jiggens P, Jun I, Meier M, Minow J I, O’Brien T P, Pitchford D, Shprits Y, Tobiska W K, Xapsos M A, Guild T B, Mazur J E, Kuznetsova M M 2019 Space Weather 17 1384 Google Scholar
[3]	Christofilos N C 1959 J. Geophys. Res. 64 869 Google Scholar
[4]	Beall D S, Bostrom C O, Williams D J 1967 J. Geophys. Res. 72 3403 Google Scholar
[5]	王建国, 刘利, 牛胜利, 左应红, 高银军, 朱金辉, 张相华, 李桠, 李夏至 2023 现代应用物理 14 3 Google Scholar Wang J G, Liu L, Niu S L, Zuo Y H, Gao Y J, Zhu J H, Zhang X H, Li Y, Li X Z 2023 Modern Appl. Phys. 14 3 Google Scholar
[6]	朱金辉, 左应红, 刘利, 牛胜利, 商鹏, 李夏至, 王学栋 2023 现代应用物理 14 44 Google Scholar Zhu J H, Zuo Y H, Liu L, Niu S L, Shang P, Li X Z, Wang X D 2023 Modern Appl. Phys. 14 44 Google Scholar
[7]	顾旭东, 赵正予, 倪彬彬, 汪枫 2009 58 5871 Google Scholar Gu X D, Zhao Z Y, Ni B B, Wang F 2009 Acta Phys. Sin 58 5871 Google Scholar
[8]	Tu W, Cunningham G S, Chen Y, Morley S K, Reeves G D, Blake J B, Baker D N, Spence H 2014 Geophys. Res. Lett. 41 1359 Google Scholar
[9]	Fok M C, Buzulukova N Y, Chen S H, Glocer A, Nagai T, Valek P, Perez J D 2014 J. Geophys. Res. Space Phys. 119 7522 Google Scholar
[10]	Fok M C, Wolf R A, Spiro R W, Moore T E 2001 J. Geophys. Res. Space Phys. 106 8417 Google Scholar
[11]	Fok M C, Kang S B, Ferradas C P, Buzulukova N Y, Glocer A, Komar C M 2021 J. Geophys. Res. Space Phys. 126 e2020JA028987 Google Scholar
[12]	Albert J M 2005 J. Geophys. Res. Space Phys. 110 A03218 Google Scholar
[13]	Albert J M 2008 J. Geophys. Res. Space Phys. 113 A06208 Google Scholar
[14]	Albert J M, Meredith N P, Horne R B 2009 J. Geophys. Res. Space Phys. 114 1DD Google Scholar
[15]	Weimer D R 2001 J. Geophys. Res. Space Phys. 106 407 Google Scholar
[16]	Tsyganenko N A 2012 J. Geophys. Res. Space Phys. 100 5599 Google Scholar
[17]	Tsyganenko N A, Stern D P 1996 J. Geophys. Res. Space Phys. 101 27187 Google Scholar
[18]	Tsyganenko N A, Mukai T 2003 J. Geophys. Res. Space Phys. 108 1136 Google Scholar
[19]	Tsyganenko N A, Sitnov M I 2005 J. Geophys. Res. Space Phys. 110 A03208 Google Scholar
[20]	Meredith N P, Horne R B, Thorne R M, Summers D, Anderson R R 2004 J. Geophys. Res. Space Phys. 109 A06209 Google Scholar
[21]	Meredith N P, Horne R B, Sicard-Piet A, Boscher D, Yearby K H, Li W, Thorne R M 2012 J. Geophys. Res. Space Phys. 117 A10225 Google Scholar
[22]	Rairden R L, Frank L A, Craven J D 2012 J. Geophys. Res. Space Phys. 91 13613 Google Scholar
[23]	Gombosi T I, Baker D N, Balogh A, Erickson P J, Huba J D, Lanzerotti L J 2017 Space Sci. Rev. 212 985 Google Scholar
[24]	Cowee M, Winske D 2012 Update on the Electron Source Model (Los Alamos National Laboratory) DOI: 10.2172/1046529
[25]	Dyal P 2006 J. Geophys. Res. Space Phys. 111 A12211 Google Scholar
[26]	Wang J G, Niu S L, Zhang D H 2010 The Parameter Manual Book of High-Altitude Nuclear Evplosion Effect (Beijing: Atomic Energy Press) pp259–260 [王建国, 牛胜利, 张殿辉 2010 高空核爆炸效应参数手册 (北京: 原子能出版社) 第259—260页] Wang J G, Niu S L, Zhang D H 2010 The Parameter Manual Book of High-Altitude Nuclear Evplosion Effect (Beijing: Atomic Energy Press) pp259–260
[27]	Vette J I 1991 The AE-8 Trapped Electron Model Environment Report Number: NSSDC/WDC-A-RS-91-24
[28]	Hamlin D A, Karplus R, Vik R C, Watson K M 1961 J. Geophys. Res. 66 1 Google Scholar
[29]	Southwood D J, Kivelson M G 1981 J. Geophys. Res. Space Phys. 86 5643 Google Scholar
[30]	Southwood D J, Kivelson M G 1982 J. Geophys. Res. Space Phys. 87 1707 Google Scholar
[31]	Fei Y, Chan A A, Elkington S R, Wiltberger M J 2006 J. Geophys. Res. Space Phys. 111 A12209 Google Scholar
[32]	Lejosne S, Albert J M 2023 Frontiers in Astronomy and Space Sciences 10 1200485 Google Scholar
[33]	Lejosne S, Albert J M, Walton S D 2023 Frontiers in Astronomy and Space Sciences 10 1232512 Google Scholar
[34]	Sandhu J K, Rae I J, Wygant J R, Breneman A W, Tian S, Watt C E J, Horne R B, Ozeke L G, Georgiou M, Walach M T 2021 J. Geophys. Res. Space Phys. 126 e2020JA029024 Google Scholar
[35]	Aryan H, Bortnik J, Meredith N P, Horne R B, Sibeck D G, Balikhin M A 2020 J. Geophys. Res. Space Phys. 126 e2020JA028403 Google Scholar
[36]	Malaspina D M, Zhu H, Drozdov A Y 2020 J. Geophys. Res. Space Phys. 125 e2019JA027415 Google Scholar

[1]	Yang Hui-Hui, Ning Li-Juan. Approximate time-dependent solution of Fokker-Planck equation with non-linear drift force. Acta Physica Sinica, 2013, 62(18): 180501. doi: 10.7498/aps.62.180501
[2]	Yang Bin, Niu Sheng-Li, Zhu Jin-Hui, Huang Liu-Xing. Research of the early debris expansion from high-altitude nuclear explosions. Acta Physica Sinica, 2012, 61(20): 202801. doi: 10.7498/aps.61.202801
[3]	Ouyang Jian-Ming, Ma Yan-Yun, Shao Fu-Qiu, Zou De-Bin, Liu Jian-Xun. Numerical simulation of temporal and spatial distribution of X-ray ionization with high-altitude nuclear explosion. Acta Physica Sinica, 2012, 61(24): 242801. doi: 10.7498/aps.61.242801
[4]	Ouyang Jian-Ming, Ma Yan-Yun, Shao Fu-Qiu, Zou De-Bin. Numerical simulation of X-ray ionization and atmospheric temporal evolutions with high-altitude nuclear explosions. Acta Physica Sinica, 2012, 61(8): 083201. doi: 10.7498/aps.61.083201
[5]	Ouyang Jian-Ming, Ma Yan-Yun, Shao Fu-Qiu, Zou De-Bin. The effect of energetic electron impact ionization on radiation ionization process of high-altitude nuclear explosion. Acta Physica Sinica, 2012, 61(21): 212802. doi: 10.7498/aps.61.212802
[6]	Tao Ying-Long, Wang Jian-Guo, Niu Sheng-Li, Zhu Jin-Hui, Fan Ru-Yu. Numerical simulation of the ionization effects of prompt radiation from high-altitude nuclear explosions. Acta Physica Sinica, 2010, 59(8): 5914-5920. doi: 10.7498/aps.59.5914
[7]	Gu Xu-Dong, Zhao Zheng-Yu, Ni Bin-Bin, Wang Feng. Numerical simulation of the formation of artificial radiation belt caused by high altitude nuclear detonation. Acta Physica Sinica, 2009, 58(8): 5871-5878. doi: 10.7498/aps.58.5871
[8]	Bai Zhan-Wu, Meng Gao-Qing. The small parameter expansion solution to Fokker-Planck equation for Brownian motion in a periodic potential with internal time derivative Ornstein-Uhlenbeck noise. Acta Physica Sinica, 2008, 57(12): 7477-7481. doi: 10.7498/aps.57.7477
[9]	Zhao Chao-Ying, Tan Wei-Han. Optimum realization of the EPR paradox in the non-degenerate parametric amplification system. Acta Physica Sinica, 2006, 55(1): 19-23. doi: 10.7498/aps.55.19
[10]	Zhao Chao-Ying, Tan Wei-Han. The solution of phase-mismatched Fokker-Planck equation and its application in the QPM device. Acta Physica Sinica, 2005, 54(6): 2723-2730. doi: 10.7498/aps.54.2723
[11]	Deng Yun-Pei, Jia Tian-Qing, Leng Yu-Xin, Lu Hai-He, Li Ru-Xin, Xu Zhi-Zhan. Experimental and theoretical study on the ablation of fused silica by femtosecond lasers. Acta Physica Sinica, 2004, 53(7): 2216-2220. doi: 10.7498/aps.53.2216
[12]	Zhao Chao-Ying, Tan Wei-Han, Guo Qi-Zhi. The solution of the Fokker-Planck equation of non-degenerate parametric amplific ation system for generation of squeezed light. Acta Physica Sinica, 2003, 52(11): 2694-2699. doi: 10.7498/aps.52.2694
[13]	ZHU XUE-GUANG, KUANG GUANG-LI, ZHAO YAN-PING, LI YOU-YI, XIE JI-KANG. FOKKER-PLANCK EQUATION IN THE APPLICATION OF FAST WAVE HEATING. Acta Physica Sinica, 1998, 47(7): 1137-1142. doi: 10.7498/aps.47.1137
[14]	LU ZHI-HENG, LIN JIAN-HENG, HU GANG. A NUMERICAL STUDY OF THE FOKKER-PLANCK EQUATION FOR STOCHASTIC RESONANCE PROBLEM. Acta Physica Sinica, 1993, 42(10): 1556-1566. doi: 10.7498/aps.42.1556
[15]	QU ZHI-LIN, HU GANG. TIME-DEPENDENT SOLUTION OF THE FOKKER-PLANCK EQUATION OF NONLINEAR NONPOTENTIAL SYSTEMS. Acta Physica Sinica, 1992, 41(9): 1396-1405. doi: 10.7498/aps.41.1396
[16]	LIN REN-MING, HUANG SI-XIAN, ZHANG LIN. THE MULTI-PHOTON QUANTUM STATISTICAL THEORY OF DRIVEN OPTICAL SYSTEMS (Ⅰ)——FOKKER-PLANCK EQUATION AND GOOD CAVITY CASE. Acta Physica Sinica, 1988, 37(4): 573-581. doi: 10.7498/aps.37.573
[17]	TAN WEI-HAN, LI YU-FANG, ZHANG WEI-PING. THE FORMAL SOLUTIONS FOR FOKKER-PLANCK EQUATION WITH ZERO OR NEGATIVE DIFFUSION COEFFICIENTS AND THEIR APPLICATIONS TO QUANTUM OPTICS. Acta Physica Sinica, 1988, 37(3): 396-407. doi: 10.7498/aps.37.396
[18]	HU GANG, WANG SHENG-GUI. TIME-DEPENDENT PROBLEM OF FOKKER-PLANCK EQUATION OF MANY VARIABLES WITH A MULTI-STABLE POTENTIAL. Acta Physica Sinica, 1986, 35(6): 771-778. doi: 10.7498/aps.35.771
[19]	ZHENG WEI-MOU. EXACTLY SOLVABLE MODELS FOR THE FOKKER-PLANCK EQUATION. Acta Physica Sinica, 1986, 35(2): 247-253. doi: 10.7498/aps.35.247
[20]	HU GANG. TIME DEPENDENT SOLUTION OF FOKKER-PLANCK EQUATION WITH NON-LINEAR DRIFT FORCE. Acta Physica Sinica, 1985, 34(5): 573-580. doi: 10.7498/aps.34.573

Catalog

Vol. 74, Issue 6 - 2025-03-20

Metrics

Abstract views: 621
PDF Downloads: 34
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板