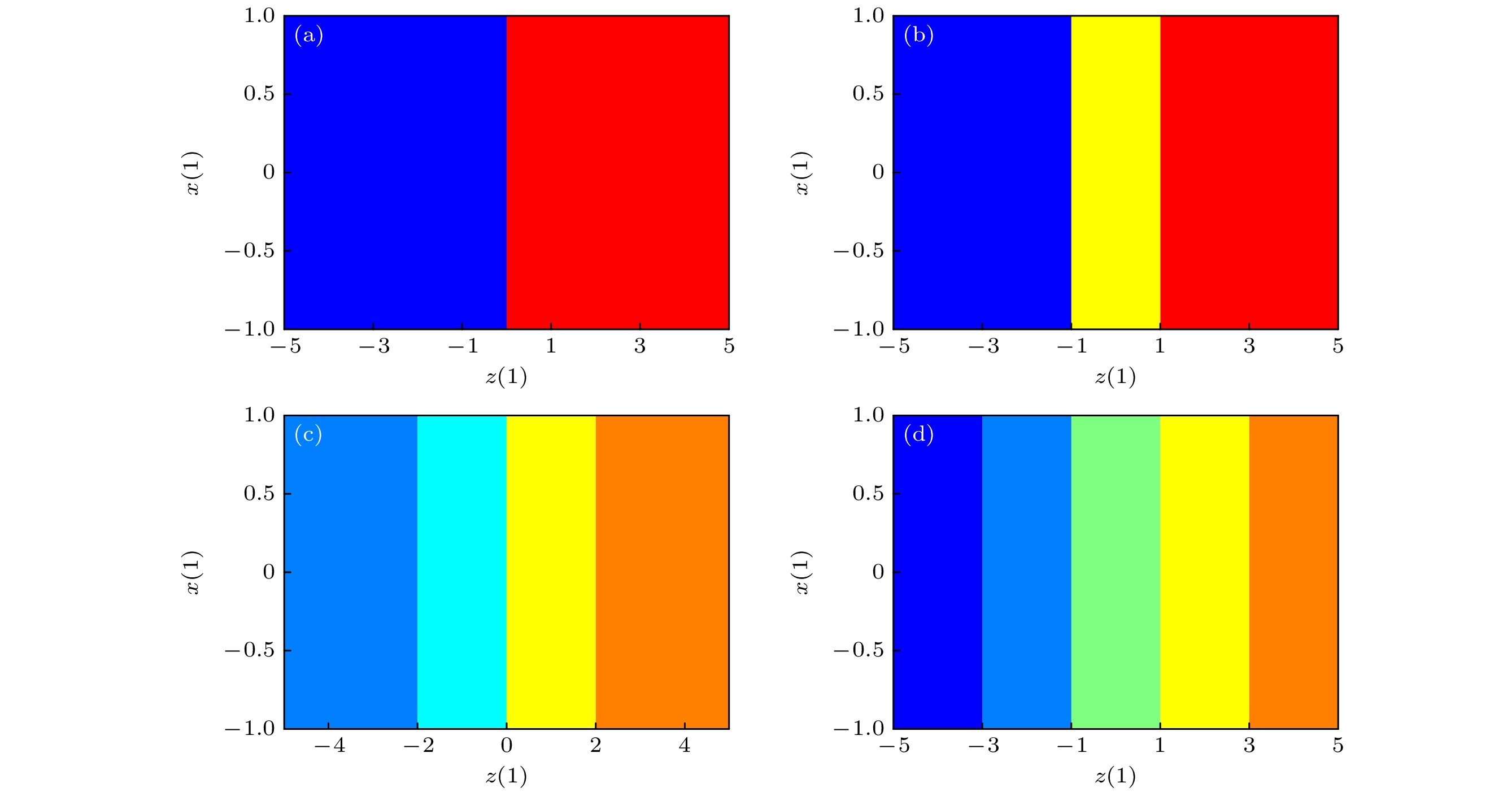
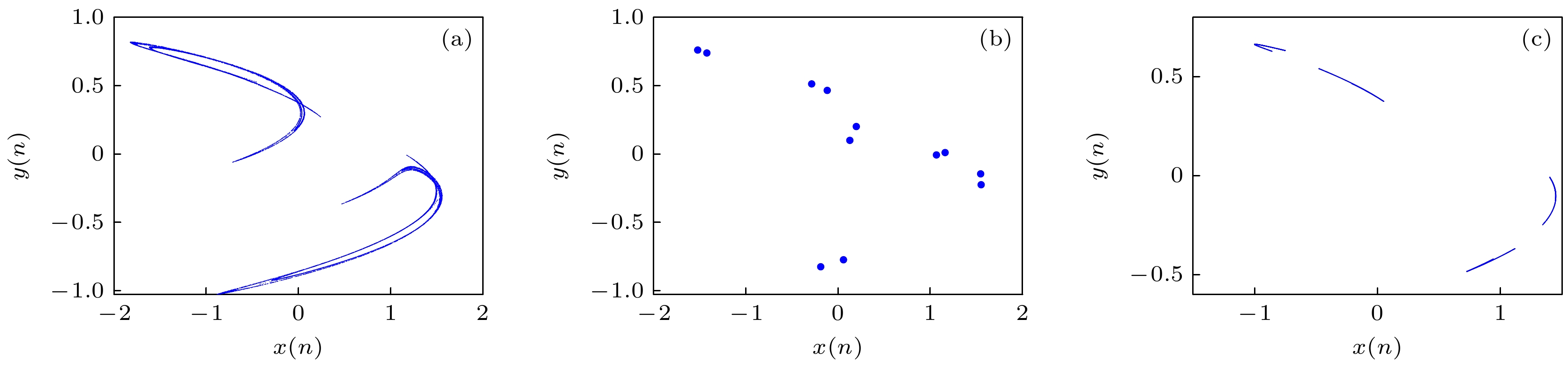
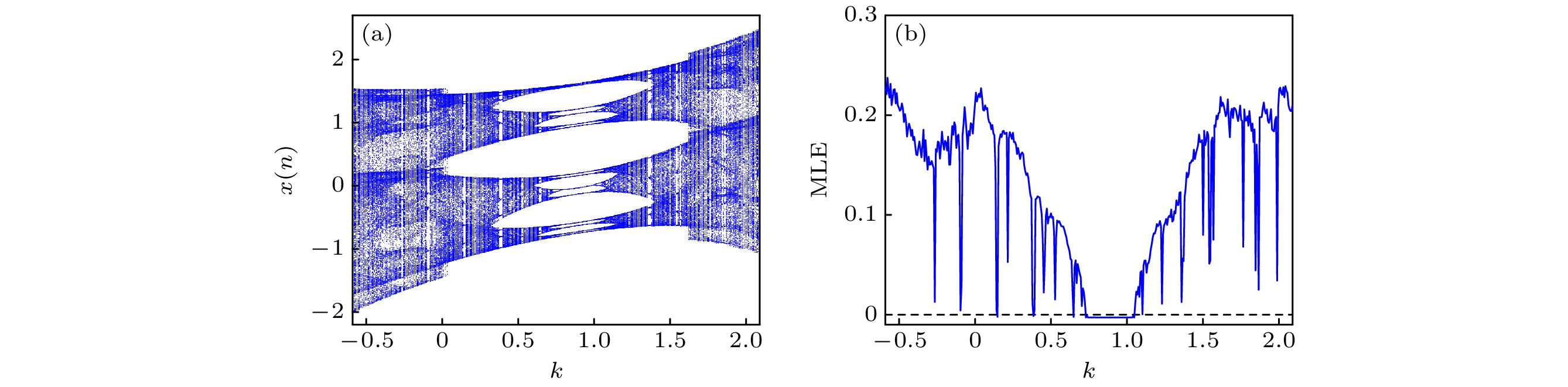
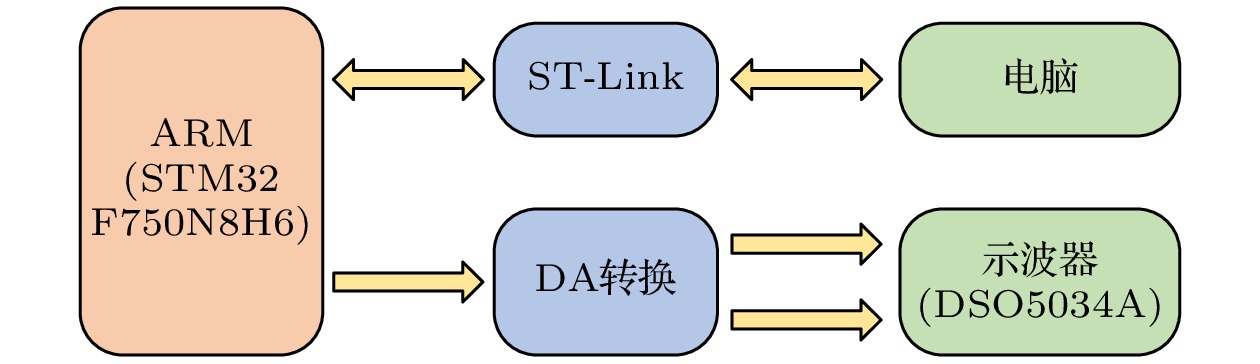
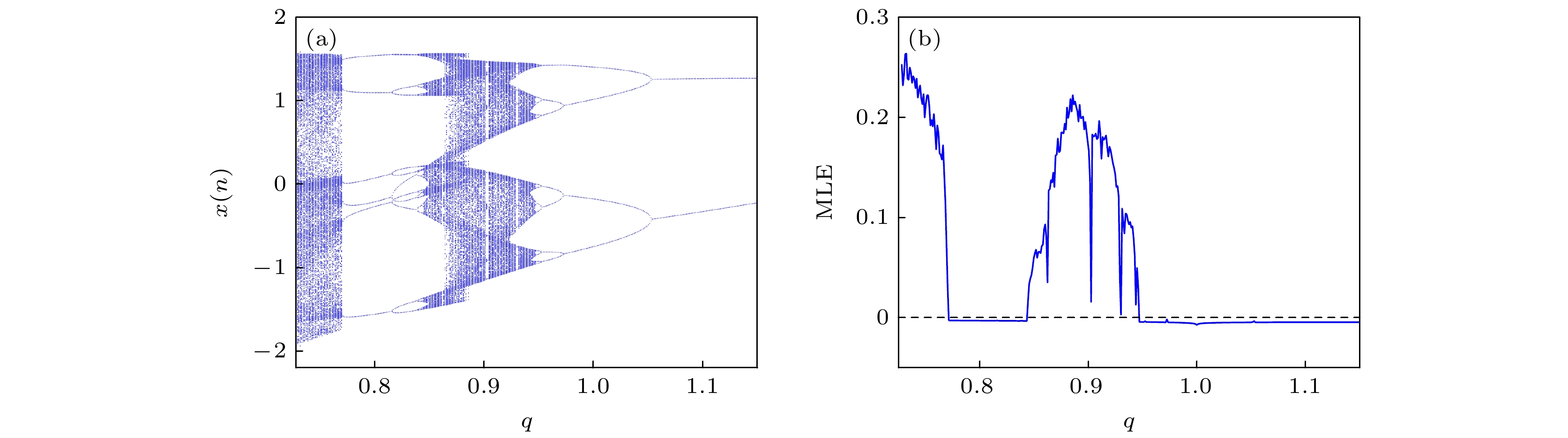
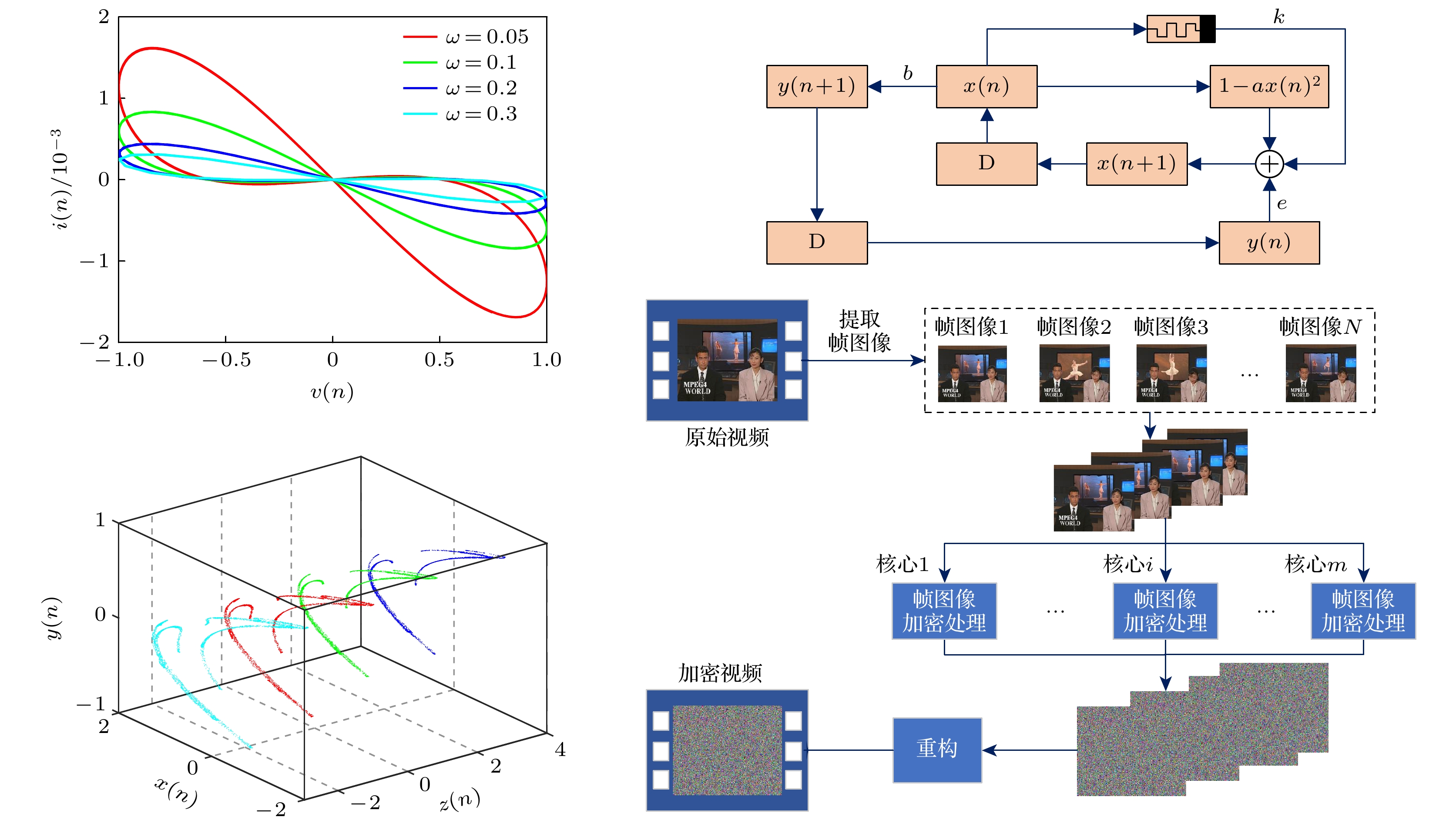
-
In recent years, the use of discrete memristors to enhance chaotic maps has received increasing attention. The introduction of memristors increases the complexity of chaotic maps, making them suitable for engineering applications based on chaotic systems. In this work, a fractional-order discrete memristor exhibiting local activity and controllable asymptotic stability points is constructed by using multiband nonlinear functions. The locally active property of this memristor is demonstrated by using the power-off plot and DC v - i plot. It is then introduced into the Henon map to construct a fractional-order memristive Henon map that can generate any number of coexisting attractors. Simulation results show that the number of fixed points in the system is controlled by the memristor parameters and related to the number of coexisting attractors, thus achieving controllable homogeneous multistability. The complex dynamical behaviors of this map are analyzed by using phase portraits, bifurcation diagrams, maximum Lyapunov exponent (MLE), and attractor basins. Numerical simulations show that the fractional-order map can generate various periodic orbits, chaotic attractors, and period-doubling bifurcations. The system is then implemented on an ARM digital platform. The experimental results are consistent with the simulation results, confirming the accuracy of the theoretical analysis and its physical feasibility. Finally, a parallel video encryption algorithm is designed by using the chaotic sequence iteratively generated by fraction-order memory Henon mapping, which mainly includes frame pixel scrambling and diffusion. Comprehensive security analyses are conducted, proving the robustness and reliability of the proposed encryption scheme. The results show that the encryption algorithm can effectively protect video information. In the future, we will explore other methods of constructing chaotic or hyperchaotic systems with controllable multistability and study their circuit implementation, synchronization control, and chaos-based engineering applications.
-
Keywords:
- fractional-order Henon map /
- locally active discrete memristor /
- controllable multistability /
- video encryption
[1] Lorenz E N 1963 J. Atmos. Sci. 20 130
Google Scholar
[2] 黄泽徽, 李亚安, 陈哲, 刘恋 2020 69 160501
Google Scholar
Huang Z H, Li Y A, Chen Z, Liu L 2020 Acta Phys. Sin. 69 160501
Google Scholar
[3] Hua Z Y, Zhou B H, Zhou Y C 2019 IEEE Trans. Ind. Electron. 66 1273
Google Scholar
[4] Zhou S, Qiu Y Y, Wang X Y, Zhang Y Q 2023 Nonlinear Dyn. 111 9571
Google Scholar
[5] Li H D, Li C L, Du J R 2023 Nonlinear Dyn. 111 2895
Google Scholar
[6] Araújo J, Gallas J A C 2021 Chaos Soliton. Fract. 150 111180
Google Scholar
[7] Lv Z W, Sun F Y, Cai C X 2022 Nonlinear Dyn. 109 3133
Google Scholar
[8] Fu L X, Wu X M, He S B, Wang H H, Sun K H 2023 IEEE Trans. Ind. Electron. 71 9668
Google Scholar
[9] Zhang S, Li C B, Zheng J H, Wang X P, Zeng Z G, Peng X N 2022 IEEE Trans. Ind. Electron. 69 7202
Google Scholar
[10] Strukov D B, Snider G S, Stewart D R, Williams R S 2008 Nature 453 80
Google Scholar
[11] 吴朝俊, 方礼熠, 杨宁宁 2024 73 010501
Google Scholar
Wu C J, Fang L Y, Yang N N 2024 Acta Phys. Sin. 73 010501
Google Scholar
[12] Pratyusha N, Mandal S 2023 Circuits Syst. Signal Process. 42 3812
Google Scholar
[13] Elsadany A A, Elsonbaty A, Hagras E A A 2023 Soft Comput. 27 4521
Google Scholar
[14] Ji X Y, Dong Z K, Han Y F, Lai C S, Zhou G D, Qi D L 2022 IEEE Trans. Consum. Electron. 69 1005
Google Scholar
[15] Ji X Y, Dong Z K, Han Y F, Lai C S, Qi D L 2023 IEEE Trans. Circuits Syst. Video Technol. 33 7928
Google Scholar
[16] 郭慧朦, 梁燕, 董玉姣, 王光义 2023 72 070501
Google Scholar
Guo H M, Liang Y, Dong Y J, Wang G Y 2023 Acta Phys. Sin. 72 070501
Google Scholar
[17] Ji X Y, Dong, Z K, Zhou G D, Lai C S, Qi D L 2024 IEEE Trans. Syst. Man. Cybern. Syst. 54 5137
Google Scholar
[18] Chua L 2014 Semicond. Sci. Technol. 29 104001
Google Scholar
[19] Ma M L, Yang Y, Qiu Z C, Peng Y X, Sun Y C, Li Z J, Wang M J 2022 Nonlinear Dyn. 107 2935
Google Scholar
[20] Lai Q, Wan Z Q, Zhang H, Chen G R 2023 IEEE Trans. Neural Netw. Learn. Syst. 34 7824
Google Scholar
[21] Zhang S, Li C B, Zheng J H, Wang X P, Zeng Z G, Chen G R 2021 IEEE Trans. Circuits Syst. I-Regul. Pap. 68 4945
Google Scholar
[22] Li H Z, Hua Z Y, Bao H, Zhu L, Chen M, Bao B C 2021 IEEE Trans. Ind. Electron. 68 9931
Google Scholar
[23] Abbes A, Ouannas A, Shawagfeh N, Khennaoui A A 2022 Eur. Phys. J. Plus 137 235
Google Scholar
[24] Zhao L D 2021 Physica A 561 125150
Google Scholar
[25] Zhao L D 2020 Circuits Syst. Signal Process. 39 6394
Google Scholar
[26] Liu X G, Ma L 2020 Appl. Math. Comput. 385 125423
Google Scholar
[27] Peng Y X, He S B, Sun K H 2021 Results Phys. 24 104106
Google Scholar
[28] Liu X, Yu Y G 2021 Neural Comput. Appl. 33 10503
Google Scholar
[29] Yang F F, Mou J, Ma C G, Cao Y H 2020 Opt. Lasers Eng. 129 106031
Google Scholar
[30] Wang Y P, Liu S T, Li H 2020 Nonlinear Dyn. 102 579
Google Scholar
[31] Ma C G, Mou J, Li P, Liu T M 2021 Eur. Phys. J. Spec. Top. 230 1945
Google Scholar
[32] Hadjadj M A, Sadoudi S, Azzaz M S, Bendecheche H, Kaibou R 2022 J. Real- Time Image Process. 19 1049
Google Scholar
[33] Dolati N, Beheshti A, Azadegan H 2021 Multimed. Tools Appl. 80 2319
Google Scholar
[34] Tabash F K, Izharuddin M 2019 Multimed. Tools Appl. 78 7365
Google Scholar
[35] Karmakar J, Pathak A, Nandi D, Mandal M K 2021 Digit. Signal Prog. 117 103143
Google Scholar
[36] Liu S C, Li Y X, Ge X Z, Li C B, Zhao Y B 2022 Phys. Scr. 97 085210
Google Scholar
[37] Li X D, Yu H Y, Zhang H Y, Jin X, Sun H B, Liu J 2020 Multimed. Tools Appl. 79 23995
Google Scholar
[38] Liu T M, Mou J, Banerjee S, Cao Y H, Han X T 2021 Nonlinear Dyn. 106 1011
Google Scholar
[39] Lu Y M, Wang C H, Deng Q L, Xu C 2022 Chin. Phys. B 31 060502
Google Scholar
[40] Lin H, Wang C, Sun Y, Yao W 2020 Nonlinear Dyn. 100 3667
Google Scholar
[41] 丁大为, 王谋媛, 王金, 杨宗立, 牛炎, 王威 2024 73 100502
Google Scholar
Ding D W, Wang M Y, Wang J, Yang Z L, Niu Y, Wang W 2024 Acta Phys. Sin. 73 100502
Google Scholar
[42] 全旭, 邱达, 孙智鹏, 张贵重, 刘嵩 2023 72 190502
Google Scholar
Quan X, Qiu D, Sun Z P, Zhang G Z, Liu S 2023 Acta Phys. Sin. 72 190502
Google Scholar
[43] 张贵重, 全旭, 刘嵩 2022 71 240502
Google Scholar
Zhang G Z, Quan X, Liu S 2022 Acta Phys. Sin. 71 240502
Google Scholar
[44] 秦铭宏, 赖强, 吴永红 2022 71 160502
Google Scholar
Qin M H, Lai Q, Wu Y H 2022 Acta Phys. Sin. 71 160502
Google Scholar
[45] El-Latif A A A, Abd-El-Atty B, Mazurczyk W, Fung C, Venegas-Andraca S E 2020 IEEE Trans. Netw. Serv. Manage. 17 118
Google Scholar
[46] Jiang D, Chen T, Yuan Z, Li W X, Wang H T, Lu L L 2024 Inf. Sci. 666 120420
Google Scholar
-
图 1 分数阶局部有源离散忆阻器的紧磁滞回线 (a) $ H = 1.0 $; (b) $ \omega = 0.001 $
Figure 1. Pinched hysteresis loops of fractional-order locally active discrete memristor: (a) $ H = 1.0 $; (b) $ \omega = 0.001 $.
图 2 分数阶局部有源离散忆阻器的POP (a) $ {I_1} = 0 $; (b) $ {I_2} = 0 $; (c) $ {I_1} = 1 $; (d) $ {I_2} = 1 $
Figure 2. POP of fractional-order locally active discrete memristor: (a) $ {I_1} = 0 $; (b) $ {I_2} = 0 $; (c) $ {I_1} = 1 $; (d) $ {I_2} = 1 $.
图 3 分数阶局部有源离散忆阻器的DC v - i图
Figure 3. DC v - i plot of fractional-order locally active discrete memristor.
图 4 忆阻Henon映射的结构图
Figure 4. Structure of memristive Henon map.
图 5 分数阶忆阻Henon映射的不动点 (a) $ {I_1} = 0 $; (b) $ {I_2} = 0 $; (c) $ {I_1} = 1 $; (d) $ {I_2} = 1 $
Figure 5. Fixed points of fractional-order memristive Henon map: (a) $ {I_1} = 0 $; (b) $ {I_2} = 0 $; (c) $ {I_1} = 1 $; (d) $ {I_2} = 1 $.
图 6 分数阶忆阻Henon映射生成的共存吸引子 (a) $ {I_1} = 0 $; (b) $ {I_2} = 0 $; (c) $ {I_1} = 1 $; (d) $ {I_2} = 1 $
Figure 6. Coexisting attractors generated by fractional-order memristive Henon map: (a) $ {I_1} = 0 $; (b) $ {I_2} = 0 $; (c) $ {I_1} = 1 $; (d) $ {I_2} = 1 $
图 7 初始值$ z(1) $的分岔图 (a) $ {I_1} = 0 $; (b) $ {I_2} = 0 $; (c) $ {I_1} = 1 $; (d) $ {I_2} = 1 $
Figure 7. Bifurcation diagrams of initial value $ z(1) $: (a) $ {I_1} = 0 $; (b) $ {I_2} = 0 $; (c) $ {I_1} = 1 $; (d) $ {I_2} = 1 $.
图 8 $ x(1){\text{-}}z(1) $平面的吸引盆 (a) $ {I_1} = 0 $; (b) $ {I_2} = 0 $; (c) $ {I_1} = 1 $; (d) $ {I_2} = 1 $
Figure 8. Attraction basins in $ x(1){\text{-}}z(1) $ plane : (a) $ {I_1} = 0 $; (b) $ {I_2} = 0 $; (c) $ {I_1} = 1 $; (d) $ {I_2} = 1 $.
图 10 当$ q $取不同值时, 分数阶忆阻Henon映射产生的吸引子 (a) $ q = 0.75 $; (b) $ q = 0.83 $; (c) $ q = 0.935 $
Figure 10. When $ q $ takes different values, the attractors generated by the fractional-order memristive Henon map: (a) $ q = 0.75 $; (b) $ q = 0.83 $; (c) $ q = 0.935 $.
图 11 当$ k \in [ - 0.59, 2.09] $时, 分数阶忆阻Henon的动力学行为 (a)分岔图; (b) MLE
Figure 11. When $ k \in [ - 0.59, 2.09] $, the dynamical behaviors of fractional-order memristive Henon map: (a) Bifurcation diagram; (b) MLE.
图 12 当$ k $取不同值时, 分数阶忆阻Henon映射产生的吸引子 (a) $ k = - 0.5 $; (b) $ k = 0.1 $; (c) $ k = 0.88 $
Figure 12. When $ k $ takes different values, the attractors generated by the fractional-order memristive Henon map: (a) $ k = - 0.5 $; (b) $ k = 0.1 $; (c) $ k = 0.88 $.
图 13 硬件实现框架
Figure 13. Framework of hardware implementation.
图 9 当$ q \in [0.728, 1.15] $时, 分数阶忆阻Henon的动力学行为 (a)分岔图; (b) MLE
Figure 9. When $ q \in [0.728, 1.15] $, the dynamical behaviors of fractional-order memristive Henon map: (a) Bifurcation diagram; (b) MLE.
图 14 阶次$ q $取不同值时的硬件实现结果 (a)硬件连接图; (b) $ q = 0.75 $; (c) $ q = 0.935 $
Figure 14. Results of hardware implementation for different values of order $ q $: (a) Hardware connection diagram; (b) $ q = $$ 0.75 $; (c) $ q = 0.935 $.
图 15 视频加密方案的流程
Figure 15. Flow of video encryption scheme.
图 16 帧图像加密的流程
Figure 16. Flow of frame image encryption.
图 17 样本视频的加密和解密结果 (a) 原始News帧图像(第1, 91, 139, 186和300帧); (b)加密帧图像; (c)解密帧图像
Figure 17. Encryption and decryption results of the sample videos: (a) Original News frame images (frames 1, 91, 139, 186 and 300); (b) encrypt frame images; (c) decrypt frame images.
图 18 原始帧图像和加密帧图像的直方图(News第91帧) (a)原始帧图像; (b)加密帧图像
Figure 18. Histograms of the original and encrypted frame image (News frame 91): (a) Original frame image; (b) encrypted frame image.
图 19 (a)—(c)原始帧图像和(d)—(f)加密帧图像(News第91帧)在3个方向上的相关性 (a), (d)水平; (b), (e)垂直; (c), (f)对角线
Figure 19. Correlation of the (a)–(c) original and (d)–(f) encrypted frame image (News frame 91) in three directions: (a), (d) Horizontal; (b), (e) vertical; (c), (f) diagonal.
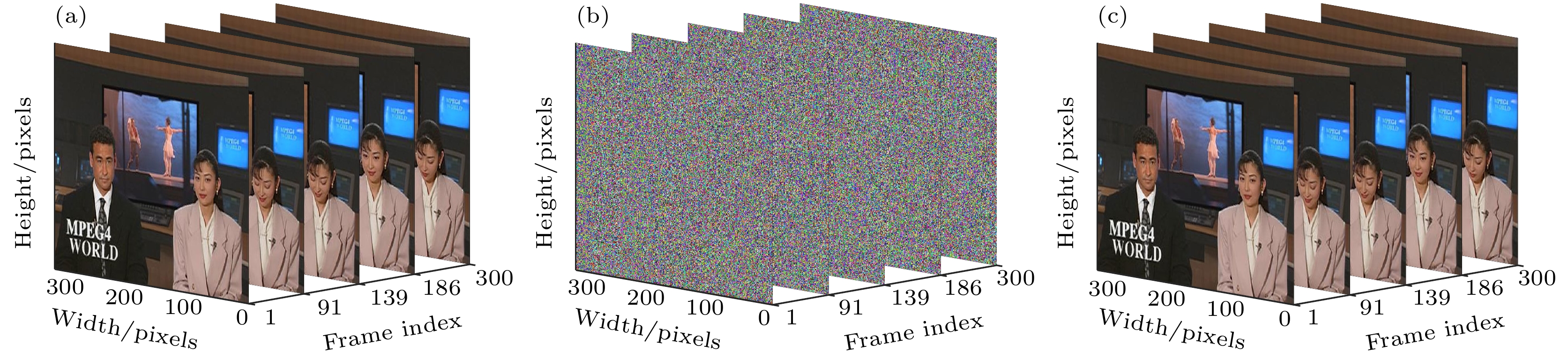
图 20 密钥敏感性分析(News第91帧) (a)使用正确密钥解密的帧图像; (b)使用错误密钥解密的帧图像($ y(1) = 0.5 + {10^{ - 16}} $); (c)使用错误密钥解密的帧图像($ q = 0.95 + {10^{ - 16}} $)
Figure 20. Key sensitivity analysis (News frame 91): (a) Decrypted frame image with the correct key; (b) decrypted frame image with the wrong key ($ y(1) = 0.5 + {10^{ - 16}} $); (c) decrypted frame image with the wrong key ($ q = 0.95 + {10^{ - 16}} $).
图 21 不同强度椒盐噪声攻击下的解密帧图像(News第91帧) (a) 10%; (b) 20%; (c) 30%
Figure 21. Decrypted frame image (News frame 91) under salt and pepper noise attack with different noise intensities: (a) 10%; (b) 20%; (c) 30%.
图 22 不同数据丢失强度下的加密帧图像和解密帧图像(News第91帧) (a), (d) 1/16; (b), (e) 1/4; (c), (f) 1/2
Figure 22. Encrypted and decrypted frame image (News frame 91) under different data loss intensities: (a), (d) 1/16; (b), (e) 1/4; (c), (f) 1/2.
表 1 原始帧图像和加密帧图像(News第91帧)在3个方向上的相关系数
Table 1. Correlation coefficients between the original frame image and the encrypted frame image (News frame 91) in three directions.
图像 方向 R G B 原始帧图像 水平 0.9536 0.9338 0.9408 垂直 0.9718 0.9618 0.9658 对角线 0.9346 0.9077 0.9173 加密后的帧图像 水平 0.0001 –0.0066 –0.0031 垂直 –0.0060 0.0014 –0.0001 对角线 –0.0004 0.0012 –0.0034 文献[45]加密帧图像 水平 0.0001 –0.0017 –0.0004 垂直 –0.0008 0.0009 0.0011 对角线 0.0001 0.0004 0.0007 
DownLoad: CSV
表 2 原始帧图像和加密帧图像(News第91帧)的信息熵
Table 2. Information entropy of original frame image and encrypted frame image (News frame 91).
R G B 原始帧图像 7.2456 7.0573 6.9584 加密后的帧图像 7.9980 7.9986 7.9985
DownLoad: CSV
表 3 与其他视频加密方案密钥空间的比较结果.
Table 3. Comparison of key spaces with other video encryption schemes.
DownLoad: CSV
-
[1] Lorenz E N 1963 J. Atmos. Sci. 20 130
Google Scholar
[2] 黄泽徽, 李亚安, 陈哲, 刘恋 2020 69 160501
Google Scholar
Huang Z H, Li Y A, Chen Z, Liu L 2020 Acta Phys. Sin. 69 160501
Google Scholar
[3] Hua Z Y, Zhou B H, Zhou Y C 2019 IEEE Trans. Ind. Electron. 66 1273
Google Scholar
[4] Zhou S, Qiu Y Y, Wang X Y, Zhang Y Q 2023 Nonlinear Dyn. 111 9571
Google Scholar
[5] Li H D, Li C L, Du J R 2023 Nonlinear Dyn. 111 2895
Google Scholar
[6] Araújo J, Gallas J A C 2021 Chaos Soliton. Fract. 150 111180
Google Scholar
[7] Lv Z W, Sun F Y, Cai C X 2022 Nonlinear Dyn. 109 3133
Google Scholar
[8] Fu L X, Wu X M, He S B, Wang H H, Sun K H 2023 IEEE Trans. Ind. Electron. 71 9668
Google Scholar
[9] Zhang S, Li C B, Zheng J H, Wang X P, Zeng Z G, Peng X N 2022 IEEE Trans. Ind. Electron. 69 7202
Google Scholar
[10] Strukov D B, Snider G S, Stewart D R, Williams R S 2008 Nature 453 80
Google Scholar
[11] 吴朝俊, 方礼熠, 杨宁宁 2024 73 010501
Google Scholar
Wu C J, Fang L Y, Yang N N 2024 Acta Phys. Sin. 73 010501
Google Scholar
[12] Pratyusha N, Mandal S 2023 Circuits Syst. Signal Process. 42 3812
Google Scholar
[13] Elsadany A A, Elsonbaty A, Hagras E A A 2023 Soft Comput. 27 4521
Google Scholar
[14] Ji X Y, Dong Z K, Han Y F, Lai C S, Zhou G D, Qi D L 2022 IEEE Trans. Consum. Electron. 69 1005
Google Scholar
[15] Ji X Y, Dong Z K, Han Y F, Lai C S, Qi D L 2023 IEEE Trans. Circuits Syst. Video Technol. 33 7928
Google Scholar
[16] 郭慧朦, 梁燕, 董玉姣, 王光义 2023 72 070501
Google Scholar
Guo H M, Liang Y, Dong Y J, Wang G Y 2023 Acta Phys. Sin. 72 070501
Google Scholar
[17] Ji X Y, Dong, Z K, Zhou G D, Lai C S, Qi D L 2024 IEEE Trans. Syst. Man. Cybern. Syst. 54 5137
Google Scholar
[18] Chua L 2014 Semicond. Sci. Technol. 29 104001
Google Scholar
[19] Ma M L, Yang Y, Qiu Z C, Peng Y X, Sun Y C, Li Z J, Wang M J 2022 Nonlinear Dyn. 107 2935
Google Scholar
[20] Lai Q, Wan Z Q, Zhang H, Chen G R 2023 IEEE Trans. Neural Netw. Learn. Syst. 34 7824
Google Scholar
[21] Zhang S, Li C B, Zheng J H, Wang X P, Zeng Z G, Chen G R 2021 IEEE Trans. Circuits Syst. I-Regul. Pap. 68 4945
Google Scholar
[22] Li H Z, Hua Z Y, Bao H, Zhu L, Chen M, Bao B C 2021 IEEE Trans. Ind. Electron. 68 9931
Google Scholar
[23] Abbes A, Ouannas A, Shawagfeh N, Khennaoui A A 2022 Eur. Phys. J. Plus 137 235
Google Scholar
[24] Zhao L D 2021 Physica A 561 125150
Google Scholar
[25] Zhao L D 2020 Circuits Syst. Signal Process. 39 6394
Google Scholar
[26] Liu X G, Ma L 2020 Appl. Math. Comput. 385 125423
Google Scholar
[27] Peng Y X, He S B, Sun K H 2021 Results Phys. 24 104106
Google Scholar
[28] Liu X, Yu Y G 2021 Neural Comput. Appl. 33 10503
Google Scholar
[29] Yang F F, Mou J, Ma C G, Cao Y H 2020 Opt. Lasers Eng. 129 106031
Google Scholar
[30] Wang Y P, Liu S T, Li H 2020 Nonlinear Dyn. 102 579
Google Scholar
[31] Ma C G, Mou J, Li P, Liu T M 2021 Eur. Phys. J. Spec. Top. 230 1945
Google Scholar
[32] Hadjadj M A, Sadoudi S, Azzaz M S, Bendecheche H, Kaibou R 2022 J. Real- Time Image Process. 19 1049
Google Scholar
[33] Dolati N, Beheshti A, Azadegan H 2021 Multimed. Tools Appl. 80 2319
Google Scholar
[34] Tabash F K, Izharuddin M 2019 Multimed. Tools Appl. 78 7365
Google Scholar
[35] Karmakar J, Pathak A, Nandi D, Mandal M K 2021 Digit. Signal Prog. 117 103143
Google Scholar
[36] Liu S C, Li Y X, Ge X Z, Li C B, Zhao Y B 2022 Phys. Scr. 97 085210
Google Scholar
[37] Li X D, Yu H Y, Zhang H Y, Jin X, Sun H B, Liu J 2020 Multimed. Tools Appl. 79 23995
Google Scholar
[38] Liu T M, Mou J, Banerjee S, Cao Y H, Han X T 2021 Nonlinear Dyn. 106 1011
Google Scholar
[39] Lu Y M, Wang C H, Deng Q L, Xu C 2022 Chin. Phys. B 31 060502
Google Scholar
[40] Lin H, Wang C, Sun Y, Yao W 2020 Nonlinear Dyn. 100 3667
Google Scholar
[41] 丁大为, 王谋媛, 王金, 杨宗立, 牛炎, 王威 2024 73 100502
Google Scholar
Ding D W, Wang M Y, Wang J, Yang Z L, Niu Y, Wang W 2024 Acta Phys. Sin. 73 100502
Google Scholar
[42] 全旭, 邱达, 孙智鹏, 张贵重, 刘嵩 2023 72 190502
Google Scholar
Quan X, Qiu D, Sun Z P, Zhang G Z, Liu S 2023 Acta Phys. Sin. 72 190502
Google Scholar
[43] 张贵重, 全旭, 刘嵩 2022 71 240502
Google Scholar
Zhang G Z, Quan X, Liu S 2022 Acta Phys. Sin. 71 240502
Google Scholar
[44] 秦铭宏, 赖强, 吴永红 2022 71 160502
Google Scholar
Qin M H, Lai Q, Wu Y H 2022 Acta Phys. Sin. 71 160502
Google Scholar
[45] El-Latif A A A, Abd-El-Atty B, Mazurczyk W, Fung C, Venegas-Andraca S E 2020 IEEE Trans. Netw. Serv. Manage. 17 118
Google Scholar
[46] Jiang D, Chen T, Yuan Z, Li W X, Wang H T, Lu L L 2024 Inf. Sci. 666 120420
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 1122
- PDF Downloads: 44
- Cited By: 0
