-
In order to observe the extraordinary optical transmission (EOT) through a metal gratings, induced by Tamm plasmon polaritons (TPPs), a layered structure consisting of a distributed Bragg reflector covered with a one-dimensional metal grating is proposed in this work. When an incident light wave passes through DBR regime and impinges on the DBR-metal interface normally, the generation of TPPs and the resulting highly localized energy on the metal-DBR interface are simulated in detail by the finite element method. As a result, the surface plasmon polariton (SPPs) modes accommodated inside the slits of metal gratings can be excited more effectively by the enhanced electromagnetic field associated with TPPs located on the interface. Furthermore, the enhanced transmission of incident light waves in the structure can be achieved when the SPP mode inside the grating slits satisfies the Fabry-Perot (FP)-like resonance condition, which reveals that the EOT in this structure comes from a TPPs-FP hybrid resonance. This inference can be confirmed by the relationships between the central wavelength and the grating height for the two transmission peaks, and the magnetic field modal profiles associated with the two peaks. Quantitative effects of the slit width and duty cycle on the transmission peak of the metal grating are analyzed numerically, and the results demonstrate that when the period is determined, as the slits width increases, the two peak transmittances first increase and then decrease. On the other hand, when the slit widths are chosen to be 40 nm, 50 nm, and 60 nm respectively, the peak transmittance first increases and then decreases with the duty cycle increasing. Meanwhile, it is found that the center wavelengths of the transmission peaks are related to the duty cycle in a nearly linear manner for three slit widths, which can be used to flexibly adjust the center wavelength of extraordinary optical transmission.
-
Keywords:
- extraordinary optical transmission /
- metal grating /
- Tamm plasmon polaritons /
- quasi Fabry-Perot resonance
[1] Ebbesen T W, Lezee H J, Ghaemi H F, Thio T, Wolff P A 1998 Nature 391 667
Google Scholar
[2] Ghaemi H F, Thio Tineke, Grupp D E, Ebbesen T W, Lezec H J 1998 Phys. Rev. B 58 6779
Google Scholar
[3] Martín-Moreno L, García-Vidal F J, Lezec H J, PellerinK M, Thio T, Pendry J B, Ebbesen T W 2001 Phys. Rev. Lett. 86 1114
Google Scholar
[4] Barnes W L, Murray W A, Dintinger J, Devaux E, Ebbesen T W 2004 Phys. Rev. Lett. 92 107401
Google Scholar
[5] 张鑫, 刘海涛 2016 物理学进展 36 118
Zhang X, Liu H T 2016 Prog. Phys. 36 118
[6] Takakura Y 2001 Phys. Rev. Lett. 86 5601
Google Scholar
[7] Ruan Z C, Qiu M 2006 Phys Rev. Lett. 96 233901
Google Scholar
[8] 聂俊英, 张宛, 罗李娜, 李贵安, 郑海荣, 张中月 2015 中国科学: 物理学 力学 天文学 45 024202
Google Scholar
Nie J Y, Zhang W, Luo L N, Li G A, Zheng H R, Zhang Z Y 2015 Sci. Sin-Phys. Mech Astron. 45 024202
Google Scholar
[9] Genet C, Ebbesen T W 2007 Nature 445 39
Google Scholar
[10] 王振林 2009 物理学进展 29 287
Google Scholar
Wang Z L 2009 Prog. Phys. 29 287
Google Scholar
[11] Kaliteevski M, Iorsh I, Brand S, Abram R A, Chamberlain J M, Kavokin A V, Shelykh I A 2007 Phys. Rev. B 76 165415
Google Scholar
[12] Sasin M E, Seisyan R P, Kalitteevski M A, Brand S, Abram A, Chamberlain J M, Egorov A Yu, Vasilev A P, Mikhrin V S, Kavokin A V 2008 Appl. Phys. Lett. 92 251112
Google Scholar
[13] Zhou H C, Yang G, Wang K, Long H, Lu P X 2010 Opt. Lett. 35 4112
Google Scholar
[14] Afinogenov B I, Bessonov V O, Nikulin A A, Fedyanin A A 2013 Appl. Phys. Lett. 103 061112
Google Scholar
[15] Das R, Srivastava T, Jha R 2014 Opt. Lett. 39 896
Google Scholar
[16] Das D, Bover P, Salvi J 2021 Appl. Opt. 60 4738
Google Scholar
[17] 陆云清, 成心怡, 许敏, 许吉, 王瑾 2016 65 204207
Google Scholar
Lu Y Q, Cheng X Y, Xu M, Xu J, Wang J 2016 Acta Phys. Sin. 65 204207
Google Scholar
[18] 祁云平, 周培阳, 张雪伟, 严春满, 王向贤 2018 67 107104
Google Scholar
Qi Y P, Zhou P Y, Zhang X W, Yan C M, Wang X X 2018 Acta Phys. Sin. 67 107104
Google Scholar
[19] García-Vidal F J, Lezec H J, Ebbesen T W, Martín-Moreno L 2003 Phys. Rev. Lett. 90 213901
Google Scholar
[20] 丁冠天, 关建飞, 陈陶, 陆云清 2023 光学学报 43 1428002
Google Scholar
Ding G T, Guan J F, Chen T, Lu Y Q 2023 Acta Opt. Sin. 43 1428002
Google Scholar
[21] Gordon R 2006 Phys. Rev. B 73 153405
Google Scholar
-
图 1 金属光栅覆盖DBR结构示意图
Figure 1. Schematic diagram of DBR structure coated with a metal grating.
图 2 TM模式入射金属层覆盖DBR结构及纯TiO2介质产生的透射及反射谱图
Figure 2. Transmission and reflection spectra generated in a perfect metal layer capped the DBR structure and the semi-infinite TiO2 media.
图 3 1040 nm光波入射到金属银覆盖DBR结构及金属银覆盖TIO2中的能量分布 (a) 周期单元模场分布图; (b) z轴方向磁场截线图
Figure 3. Energy distribution in the silver covered DBR structure and silver capped TiO2 dielectric generated by the incident light wave of 1040 nm: (a)Magnetic field $ \left| {{H_y}} \right| $ distribution at λ = 1040 nm; (b) magnetic field $ \left| {{H_y}} \right| $ profile along z axis.
图 4 TE及TM光波入射到金属光栅-DBR结构产生的透射及反射谱线图 (a) 透射谱; (b) 反射谱
Figure 4. Transmission and reflection spectra generated by the TE and TM polarized incident light waves in the metal grating capped DBR: (a) Transmission spectra; (b) reflection spectra.
图 5 (a) TM和TE模式入射产生磁场强度分布; (b)磁场分量$ \left| {{H_y}} \right| $沿中心轴线的分布图
Figure 5. (a) Distribution of the magnetic field component $ \left| {{H_y}} \right| $ for TM and TE waves; (b) the profile of the magnetic component $ \left| {{H_y}} \right| $ along the axis of x = 0.
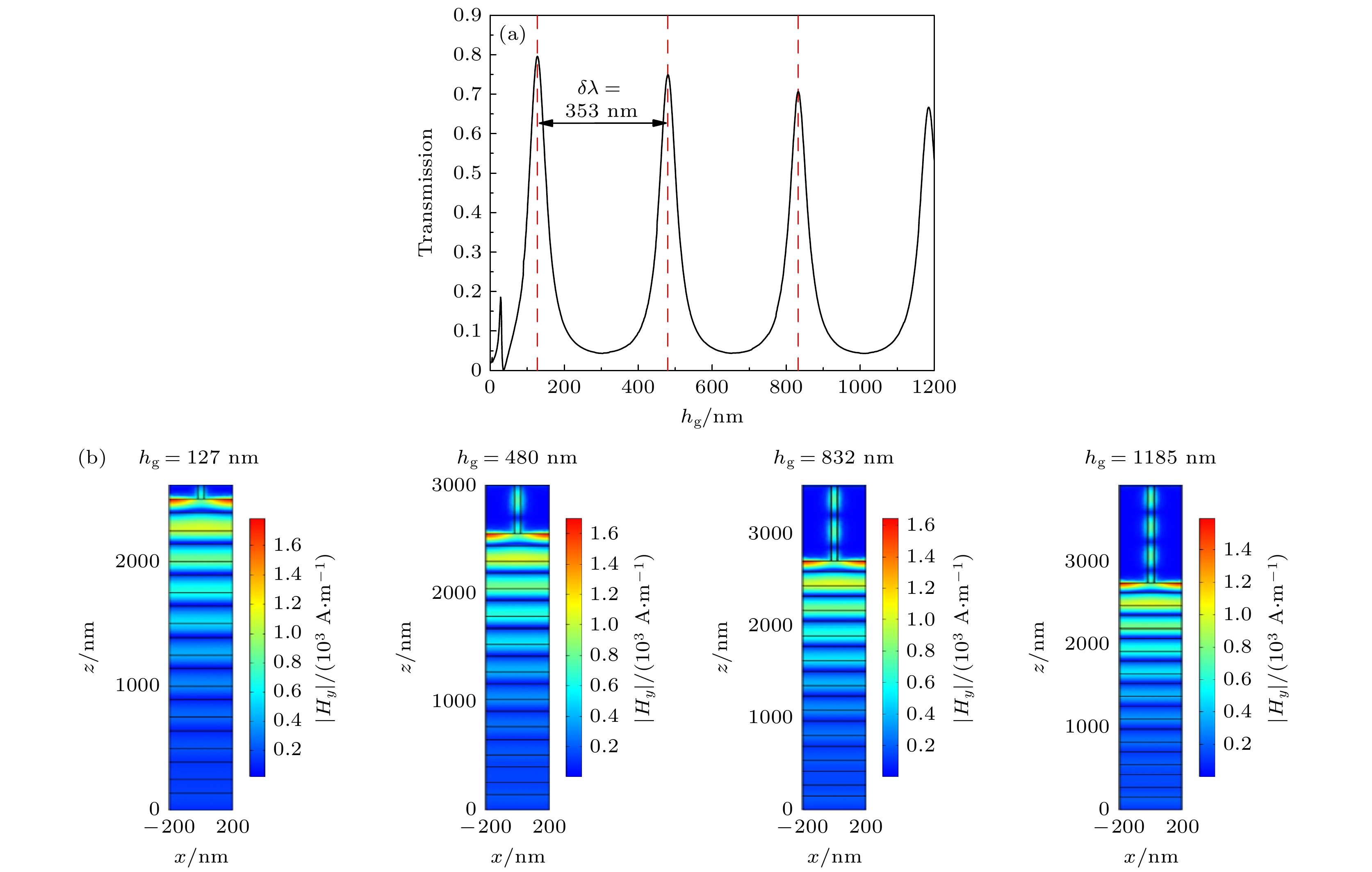
图 6 (a) 透射率随金属光栅高度的变化关系; (b) 透射峰值处的模场分布图
Figure 6. (a) The transmittance as a function of the grating heights for TM polarization; (b) magnetic field intensity distributions for the four transmission peaks depicted in Fig. 6(a).
图 7 不同缝宽的透射谱线随光栅高度的演变规律 (a) w = 40 nm; (b) w = 50 nm; (c) w = 60 nm.
Figure 7. Transmittance against incident wavelengths and grating heights for three slit widths: (a) w = 40 nm; (b) w = 50 nm; (c) w = 60 nm.
图 8 前两阶谐振透射峰的峰值幅度(a)与中心波长λ (b)随狭缝宽度w的演变规律
Figure 8. Evolution of (a) amplitudes and (b) central wavelengths λ of the transmittance peaks generated by the first and second order resonances with slit widths w.
图 9 一阶谐振透射峰的峰值透射峰率(a)及中心波长(b)随周期的变化规律
Figure 9. Evolutions of (a) amplitudes and (b) central wavelength λ of the transmittance peak generated by the first order resonance with grating periods for three slit widths.
图 10 一阶谐振透射峰的峰值透射峰率(a)及中心波长(b)随占空比的变化规律
Figure 10. Evolutions of (a) amplitudes and (b) central wavelength λ of the transmittance peak generated by the first order resonance with duty cycles for three slit widths.
-
[1] Ebbesen T W, Lezee H J, Ghaemi H F, Thio T, Wolff P A 1998 Nature 391 667
Google Scholar
[2] Ghaemi H F, Thio Tineke, Grupp D E, Ebbesen T W, Lezec H J 1998 Phys. Rev. B 58 6779
Google Scholar
[3] Martín-Moreno L, García-Vidal F J, Lezec H J, PellerinK M, Thio T, Pendry J B, Ebbesen T W 2001 Phys. Rev. Lett. 86 1114
Google Scholar
[4] Barnes W L, Murray W A, Dintinger J, Devaux E, Ebbesen T W 2004 Phys. Rev. Lett. 92 107401
Google Scholar
[5] 张鑫, 刘海涛 2016 物理学进展 36 118
Zhang X, Liu H T 2016 Prog. Phys. 36 118
[6] Takakura Y 2001 Phys. Rev. Lett. 86 5601
Google Scholar
[7] Ruan Z C, Qiu M 2006 Phys Rev. Lett. 96 233901
Google Scholar
[8] 聂俊英, 张宛, 罗李娜, 李贵安, 郑海荣, 张中月 2015 中国科学: 物理学 力学 天文学 45 024202
Google Scholar
Nie J Y, Zhang W, Luo L N, Li G A, Zheng H R, Zhang Z Y 2015 Sci. Sin-Phys. Mech Astron. 45 024202
Google Scholar
[9] Genet C, Ebbesen T W 2007 Nature 445 39
Google Scholar
[10] 王振林 2009 物理学进展 29 287
Google Scholar
Wang Z L 2009 Prog. Phys. 29 287
Google Scholar
[11] Kaliteevski M, Iorsh I, Brand S, Abram R A, Chamberlain J M, Kavokin A V, Shelykh I A 2007 Phys. Rev. B 76 165415
Google Scholar
[12] Sasin M E, Seisyan R P, Kalitteevski M A, Brand S, Abram A, Chamberlain J M, Egorov A Yu, Vasilev A P, Mikhrin V S, Kavokin A V 2008 Appl. Phys. Lett. 92 251112
Google Scholar
[13] Zhou H C, Yang G, Wang K, Long H, Lu P X 2010 Opt. Lett. 35 4112
Google Scholar
[14] Afinogenov B I, Bessonov V O, Nikulin A A, Fedyanin A A 2013 Appl. Phys. Lett. 103 061112
Google Scholar
[15] Das R, Srivastava T, Jha R 2014 Opt. Lett. 39 896
Google Scholar
[16] Das D, Bover P, Salvi J 2021 Appl. Opt. 60 4738
Google Scholar
[17] 陆云清, 成心怡, 许敏, 许吉, 王瑾 2016 65 204207
Google Scholar
Lu Y Q, Cheng X Y, Xu M, Xu J, Wang J 2016 Acta Phys. Sin. 65 204207
Google Scholar
[18] 祁云平, 周培阳, 张雪伟, 严春满, 王向贤 2018 67 107104
Google Scholar
Qi Y P, Zhou P Y, Zhang X W, Yan C M, Wang X X 2018 Acta Phys. Sin. 67 107104
Google Scholar
[19] García-Vidal F J, Lezec H J, Ebbesen T W, Martín-Moreno L 2003 Phys. Rev. Lett. 90 213901
Google Scholar
[20] 丁冠天, 关建飞, 陈陶, 陆云清 2023 光学学报 43 1428002
Google Scholar
Ding G T, Guan J F, Chen T, Lu Y Q 2023 Acta Opt. Sin. 43 1428002
Google Scholar
[21] Gordon R 2006 Phys. Rev. B 73 153405
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 1638
- PDF Downloads: 52
- Cited By: 0
