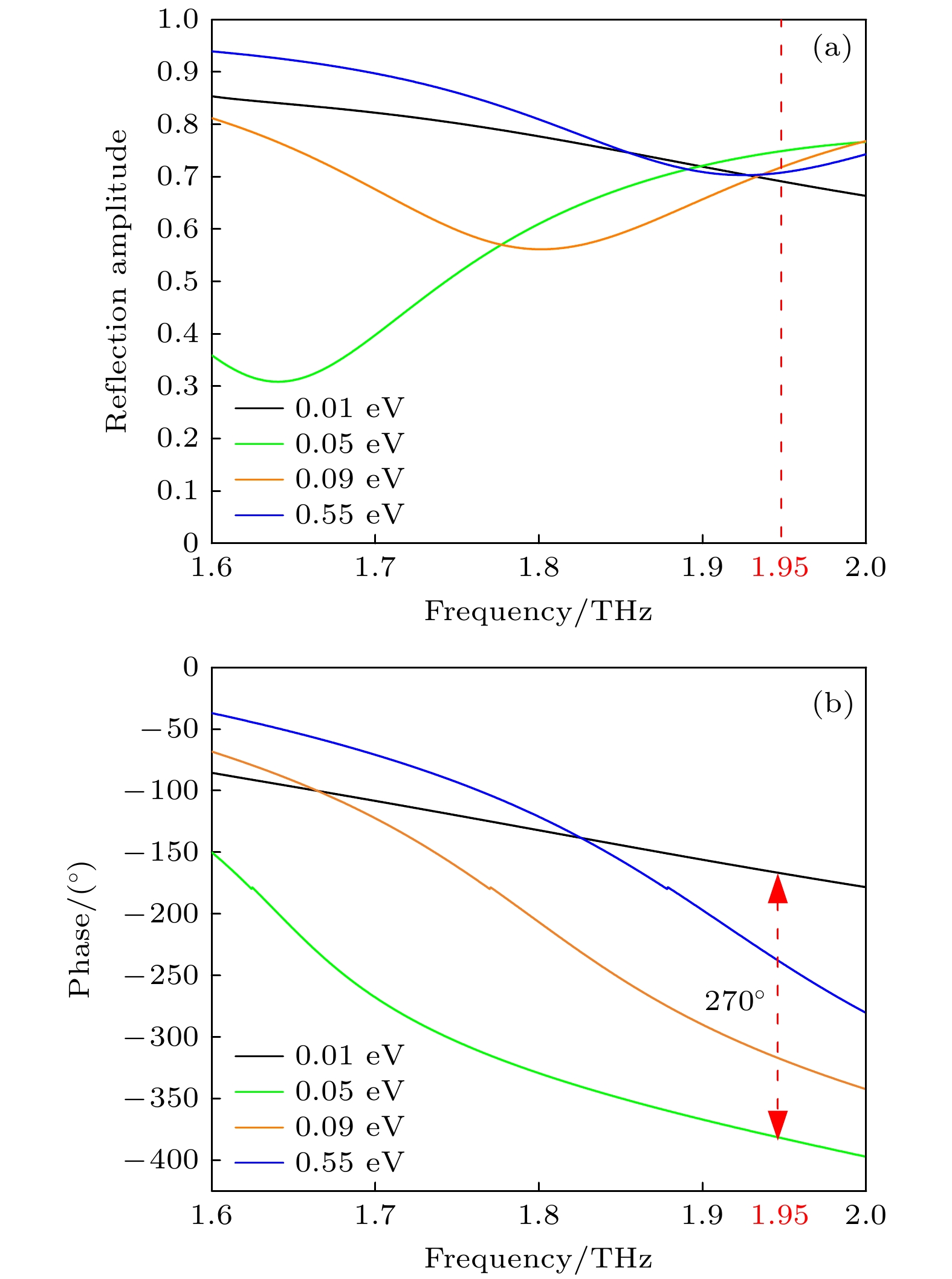
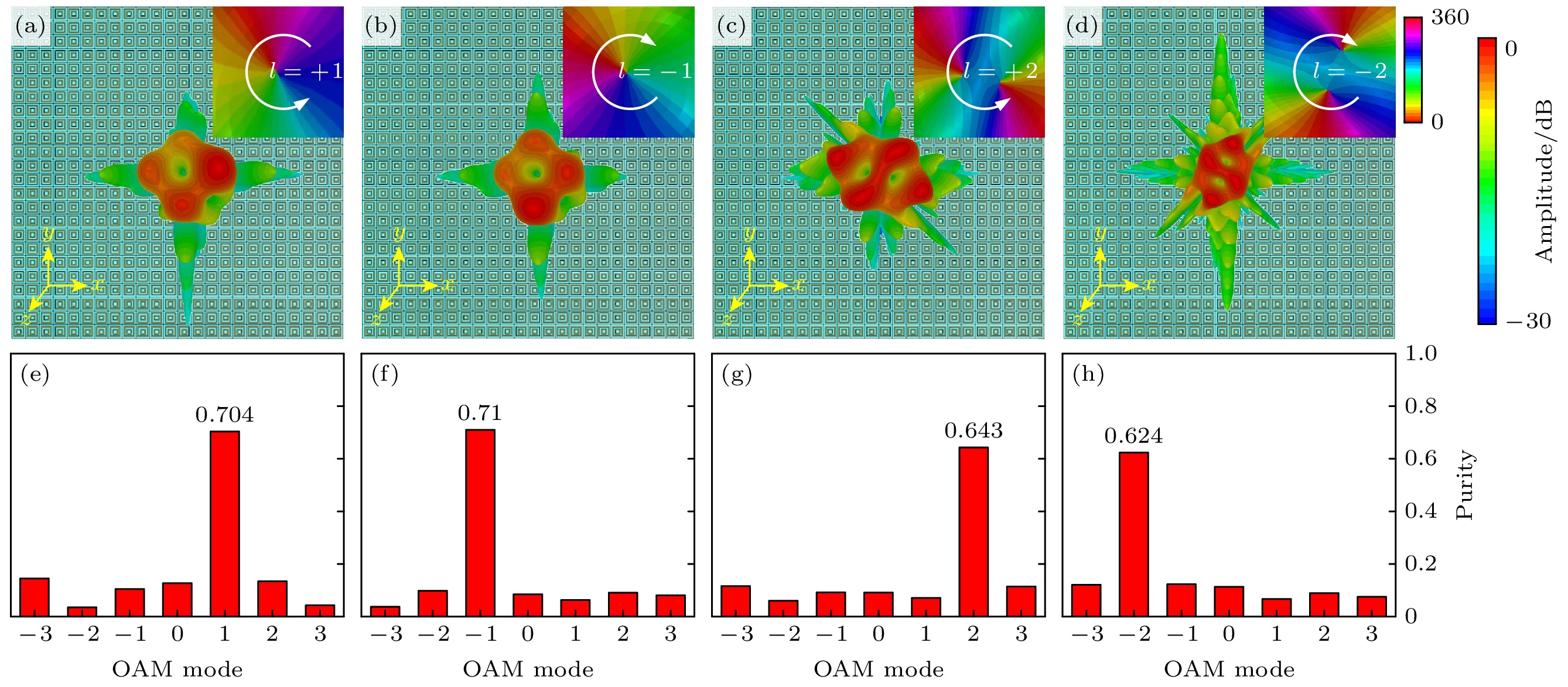
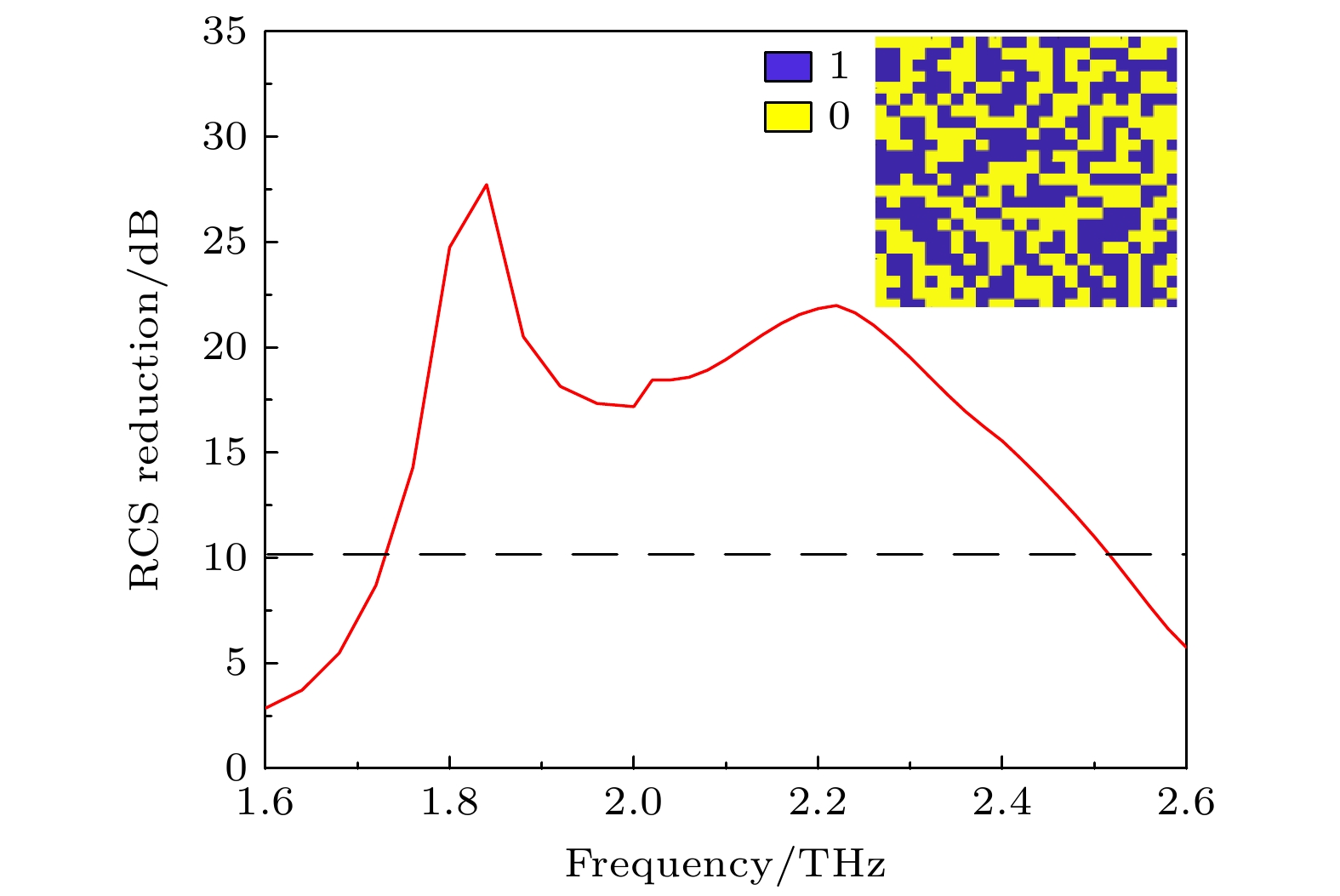
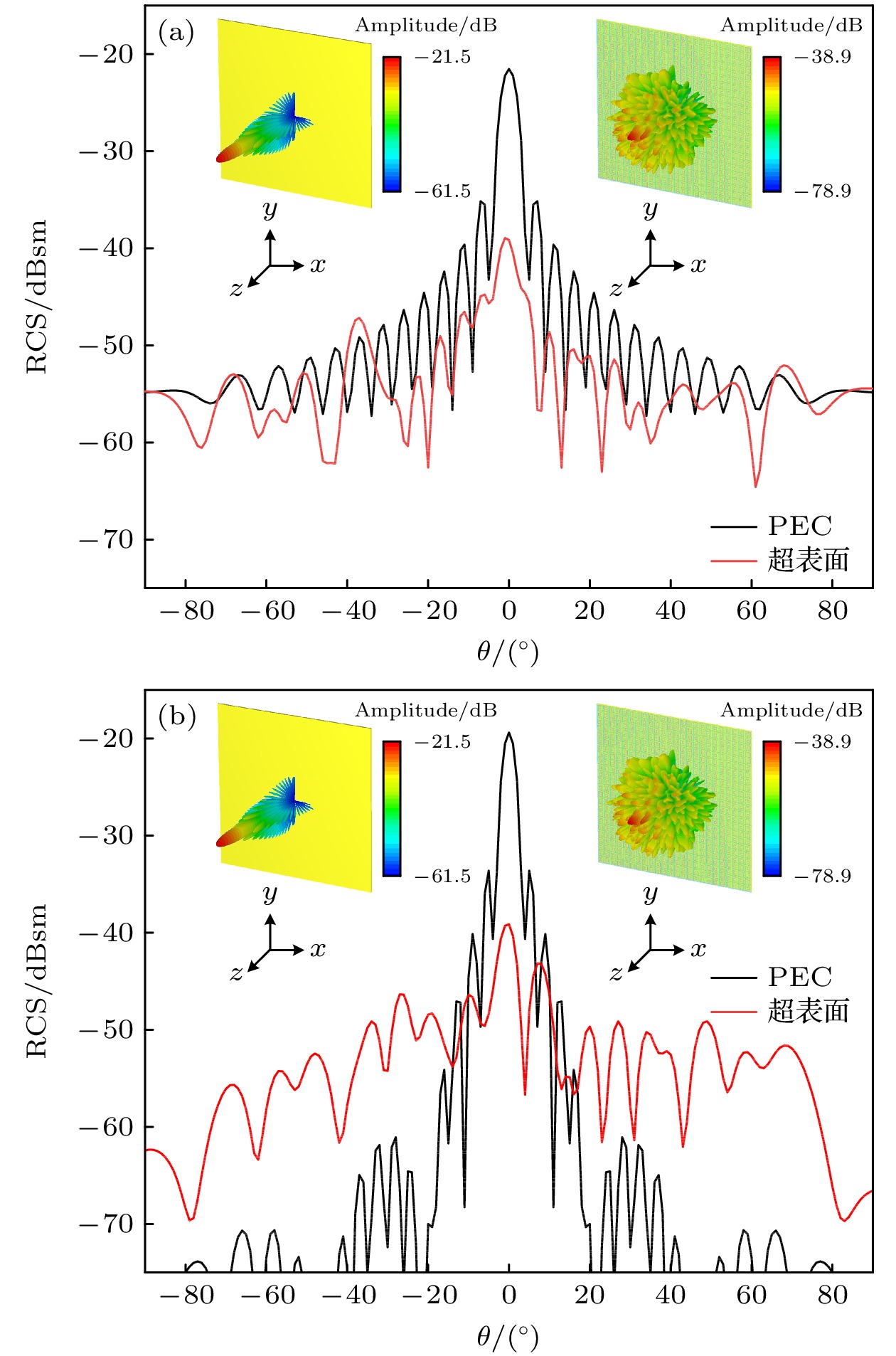
-
Digitally encoded hypersurfaces show great potential in the field of electromagne-tic wave modulation. Currently, digitally encoded hypersurfaces in the terahertz band are mainly classified into two types: structure-encoded and controllable material-encoded. Once a structure-encoded hypersurface is fabricated, its function is fixed, which makes it difficult to adapt to changing application requirements. In contrast, the controllable material-encoded hypersurfaces can achieve dynamic regulation and multifunctional switching of terahertz beams by changing the external excitation, which shows good reconfigurability. To address this challenge, a Dirac semimetal-based encoded hypersurface is proposed in this paper. The Fermi energy level of the Dirac semimetal is varied by changing the bias voltage, which in turn dynamically adjusts its relative permittivity to obtain the coded unit. Besides, the traditional gradient-phase method encodes arrays by periodically arranging the cell structure, but there are limitations in the flexibility and accuracy of beam modulation. In order to break through these limitations, this paper employs a genetic algorithm for the inverse design of hypersurface coding arrays, which effectively improves the initiative and flexibility of beam modulation. In this paper, a three-layer terahertz-encoded hypersurface unit with a “back” structure composed of Dirac semimetallic materials is firstly designed, and the Dirac semimetallic dielectric constant is dynamically adjusted by using an applied bias voltage, so that the hypersurface unit is at 1.95 THz when the Fermi energy levels are 0.01 eV, 0.05 eV, 0.09 eV, and 0.55 eV can achieve 2bit coding. The results show that, for beam configuration, single-beam and multi-beam (two-beam to five-beam) modulation can be achieved at 1.95 THz within 40° pitch angle and 360° azimuth angle; for vortex beam generation, single-vortex beams with ±1 and ±2 topological charges can be generated, with mode purity exceeding 60%, and single-vortex, double-vortex and triple-vortex beams in pitch angle and 360° azimuth angle can be realised with the vortex-phase convolution. In terms of RCS reduction, in the frequency range of 1.72–2.51 THz, the hypersurface is able to achieve more than 10 dB of RCS reduction, especially in the frequency range of 1.82 THz, the maximum reduction value is up to 27.5 dB. achieves the diversity of functions, but also has a high degree of reconfigurability to meet the needs of complex application scenarios.
[1] Davies A G, Linfield E H, Johnston M B 2002 Phys. Med. Biol. 47 3679
Google Scholar
[2] Yu N F, Genevet P, Kats M A, Aieta F, Tetienne J P, Capasso F, Gaburro Z 2011 Science 334 333
Google Scholar
[3] Zhang X Q, Tian Z, Yue W S, Gu J Q, Zhang S, Han J G, Zhang W L 2013 Adv. Mater. 25 4567
Google Scholar
[4] Cui T J, Qi M Q, Wan X, Zhao J, Cheng Q 2014 Light Sci. Appl. 3 e218
Google Scholar
[5] Zhang L, Wu R Y, Bai G D, Wu H T, Mu H T, Ma Q, Chen X Q, Cui T J 2018 Adv. Funct. Mater. 28 1802205
Google Scholar
[6] 黄若彤, 李九生 2023 72 054203
Google Scholar
Huang R T, Li J S 2023 Acta Phys. Sin. 72 054203
Google Scholar
[7] Nie R X, He C H, Zhang R X, Song Z Y 2023 Opt. Laser Technol. 159 109010
Google Scholar
[8] Zhao Y Z, Huang C, Song Z L, Yu C Y, Liang S, Luo X G, Qing A Y 2019 IEEE Access 7 79671
Google Scholar
[9] 李佳辉, 张雅婷, 李吉宁, 李杰, 李继涛, 郑程龙, 杨悦, 黄进, 马珍珍, 马承启, 郝璇若, 姚建铨 2020 69 228101
Google Scholar
Li J H, Zhang Y T, Li J N, Li J, Li J T, Zheng C L, Yang Y, Huang J, Ma Z Z, Ma C Q, Hao X R, Yao J Q 2020 Acta Phys. Sin. 69 228101
Google Scholar
[10] Xiao B G, Zhang Y, Tong S J, Yu J B, Xiao L H 2020 Opt. Express 28 7125
Google Scholar
[11] Jiang C Y, Li Z K, Lv X Y, Tian M, Liu M, Zhang H Y, Zhang Y P 2023 Opt. Commun. 540 129506
Google Scholar
[12] Yang R S, Lou J, Zhang F L, Zhu W, Xu J, Cai T, Fu Q H, Li H, Fan Y C 2021 Adv. Photonics Res. 2 2100103
Google Scholar
[13] Yang R S, Zhang F L, Li Z C, Fu Q H, Fan Y C 2023 Opt. Laser Technol. 163 109380
Google Scholar
[14] Yang R S, Fan Y C, Zhu W, Hu C J, Chen S N, Wei H, Chen W J, Chan C T, Zhao Q, Zhou J, Zhang F L, Qiu C W 2023 Laser Photonics Rev. 17 2200975
Google Scholar
[15] Wu R Y, Shi C B, Liu S, Wu W, Cui T J 2018 Adv. Opt. Mater. 6 1701236
Google Scholar
[16] 张娜, 赵健民, 陈克, 赵俊明, 姜田, 冯一军 2021 70 178102
Google Scholar
Zhang N, Zhao J M, Chen K, Zhao J M, Jiang T, Feng Y J 2021 Acta Phys. Sin. 70 178102
Google Scholar
[17] 贾宇翔, 王甲富, 陈维, 随赛, 朱瑞超, 邱天硕, 李勇峰, 韩亚娟, 屈绍波 2021 雷达学报 10 220
Google Scholar
Jia Y X, Wang J F, Chen W, Sui S, Zhu R C, Qiu T S, Li Y F, Han Y J, Qu S B 2021 J. Radars 10 220
Google Scholar
[18] 韩丁, 马子寅, 王俊林, 王鑫, 刘苏雅拉图 2022 中国激光 49 168
Han D, Ma Z Y, Wang J L, Wang X, Liu S Y L T 2022 Chin. J. Lasers 49 168
[19] Sui S, Ma H, Wang J F, Feng M D, Pang Y Q, Zhang J Q, Xu Z, Qu S B 2019 J. Phys. D: Appl. Phys. 52 035103
Google Scholar
[20] Xiao T, Liu C G, Cheng R S, Cao L F, Tang G P CNSRP Qingdao, China September 24–27, 2023 p4 (in Chinese)[肖彤, 刘成国, 程润生, 曹立锋, 唐光普 第十八届全国电波传播年会 中国青岛 2023年 9月24—27日 第4页]
[21] Kotov O V, Lozovik Y E 2016 Phys. Rev. B 93 235417
Google Scholar
[22] Liu G D, Zhai X, Meng H Y, Lin Q, Huang Y, Zhao C J, Wang L L 2018 Opt. Express 26 11471
Google Scholar
[23] Zhang X G, Tang W X, Jiang W X, Bai G D, Tang J, Bai L, Qiu C W, Cui T J 2018 Adv. Sci. 5 1801028
Google Scholar
-
图 1 基于狄拉克半金属“回”字形单元结构示意图 (a)单元俯视图; (b)单元侧视图
Figure 1. Based on Dirac semi-metal “back” font structure diagram: (a) Top view of the unit; (b) side view of the unit.
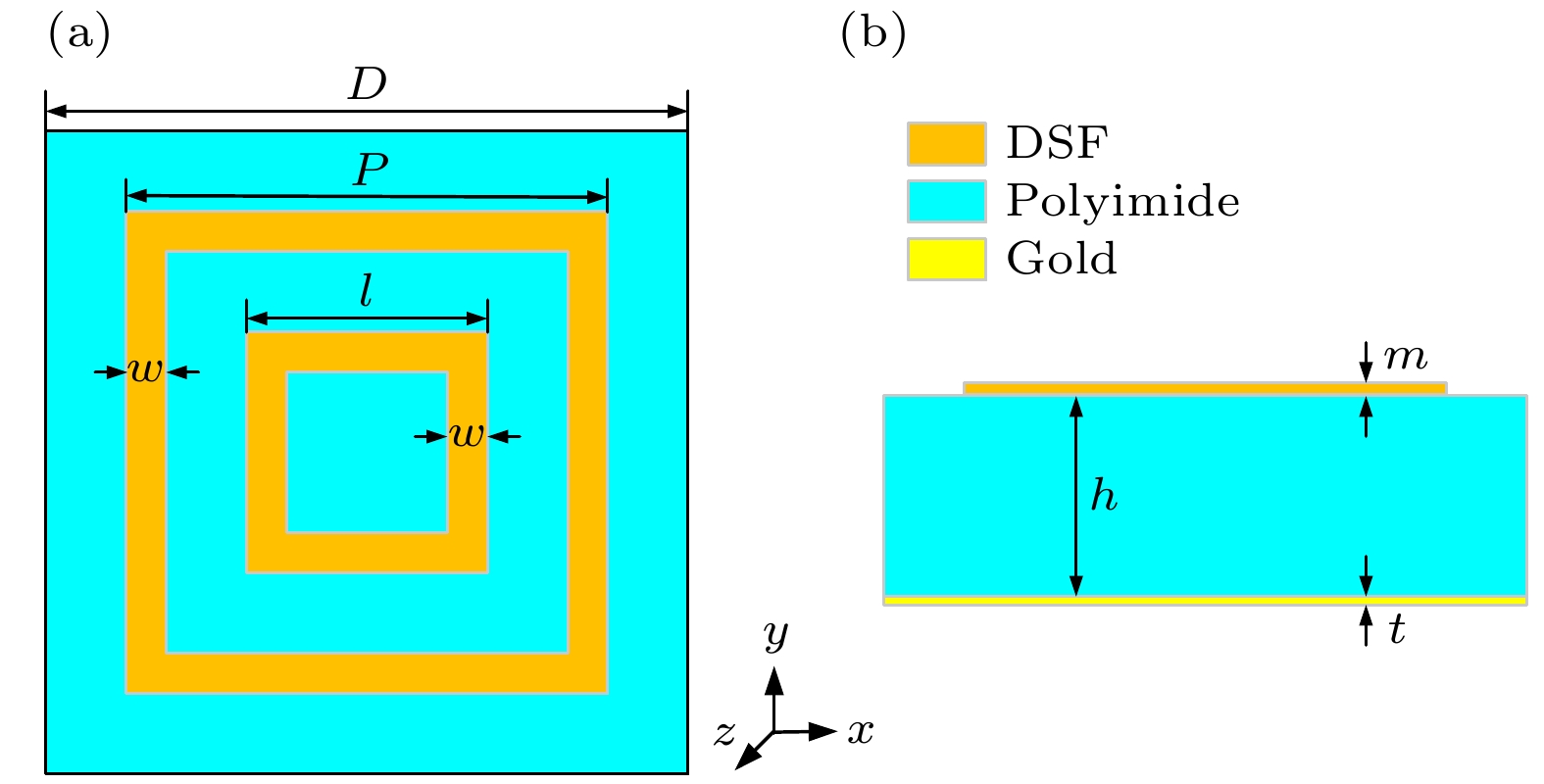
图 2 超表面单元结构在费米能级为0.09 eV时, 不同周期 D (a), 大正方形边长 P (b), 矩形条宽度 w (c), 顶层贴片厚度 m (d); 小正方形边长 l (e); 介质层厚度 h (f) 的反射幅度及反射相位曲线
Figure 2. Reflection amplitude and reflection phase curves of the hypersurface unit structure at a Fermi energy level of 0.09 eV with different (a) period D, (b) large square side length P, (c) rectangular strip width w, (d) top patch thickness m, (e) small square side length l, and (f) dielectric layer thickness h.
图 3 不同频率、不同费米能级下狄拉克半金属的相对介电常数的实部和虚部
Figure 3. The real and imaginary parts of the relative permittivity of Dirac semi-metals at different frequencies and Fermi levels.
图 4 基于遗传算法逆向设计阵列编码流程图
Figure 4. Genetic algorithm is used to reverse design array coding flow chart.
图 5 不同编码周期下迭代次数与适应度函数值之间的关系图
Figure 5. The relationship between the number of iterations and the fitness function value under different coding cycles.
图 6 超表面编码单元结构, 狄拉克半金属费米能级为0.01, 0.05, 0.09 eV及0.55 eV (a) 幅度响应曲线; (b) 相位响应曲线
Figure 6. Metasurface coding unit structure at Dirac semi-metallic Fermi level of 0.01, 0.05, 0.09 eV and 0.55 eV: (a) Amplitude response curves; (b) phase response curve.
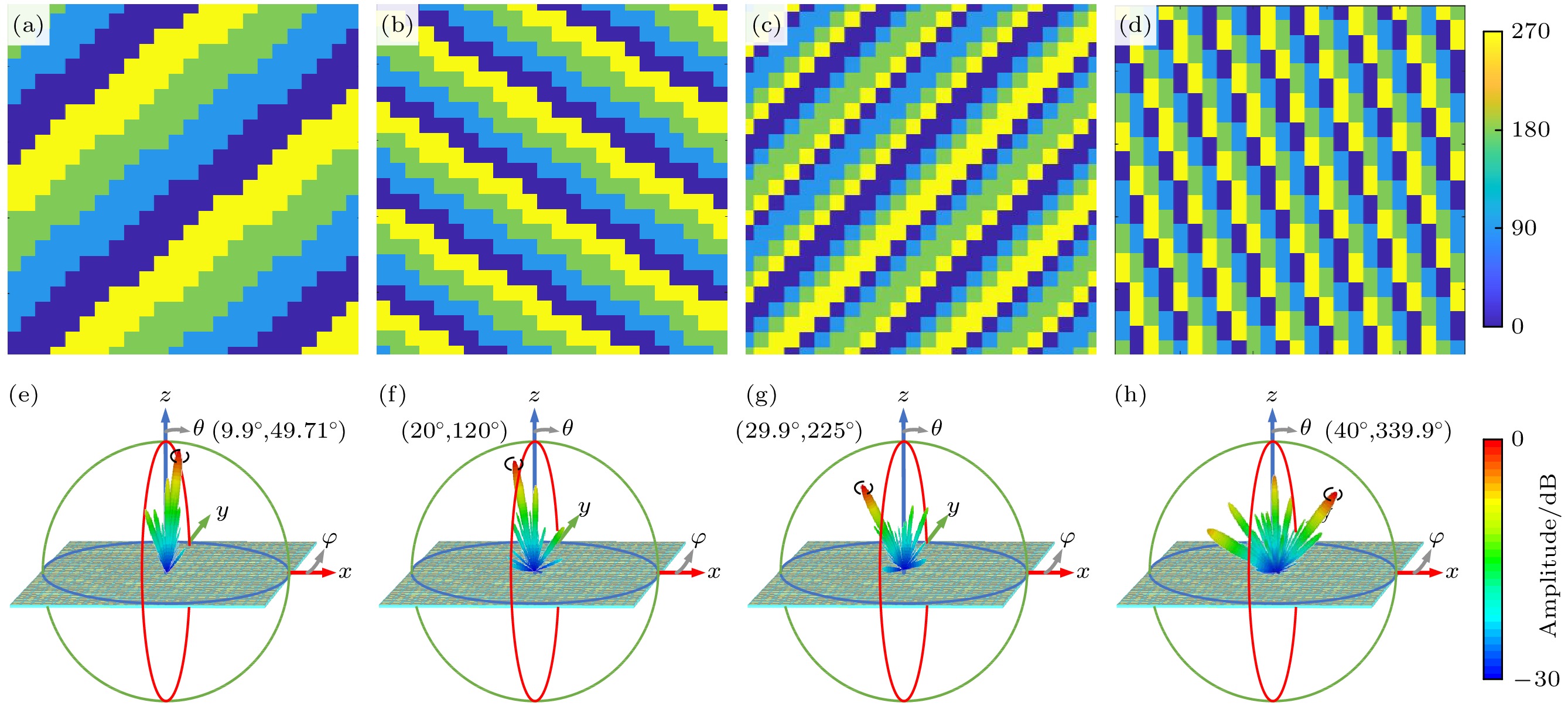
图 7 (a)—(d) $ \left( {{\theta _{{\text{ob}}}}, {\varphi _{{\text{ob}}}}} \right) $分别为(10°, 50°), (20°, 120°), (30°, 225°)及(40°, 340°)时的单波束阵列编码图样; (e)—(h) 对应的三维远场散射图
Figure 7. (a)–(d) Array coding sequence results of $ \left( {{\theta _{{\text{ob}}}}, {\varphi _{{\text{ob}}}}} \right) $ for (10°, 50°), (20°, 120°), (30°, 225°) and (40°, 340°) respectively; (e)–(h) the corresponding far-field scattering results.
图 8 1.95 THz处加运算之前和之后编码排布及三维远场散射结果
Figure 8. Pre-and post-array arrangements and 3D far-field scattering results for addition at 1.97 THz.
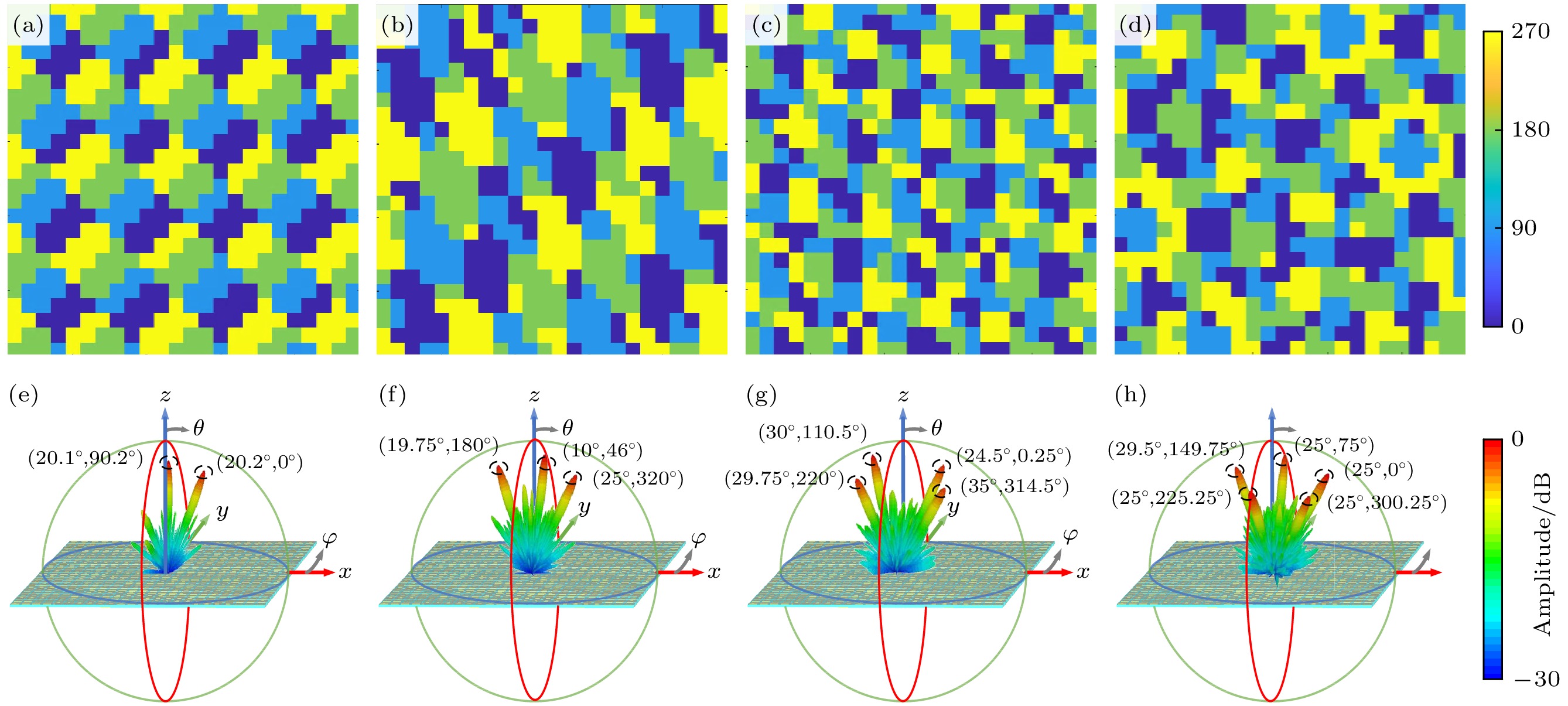
图 9 (a), (e) $ \left( {{\theta _{{\text{ob}}}}, {\varphi _{{\text{ob}}}}} \right) $分别为(20°, 0°), (20°, 90°)双波束的阵列编码图与远场散射结果; (b), (f) $ \left( {{\theta _{{\text{ob}}}}, {\varphi _{{\text{ob}}}}} \right) $分别为(10°, 45°), (20°, 180°), (25°, 320°)三波束的阵列编码图与远场散射结果; (c), (g) $ \left( {{\theta _{{\text{ob}}}}, {\varphi _{{\text{ob}}}}} \right) $分别为(25°, 0°), (30°, 110°), (30°, 220°), (35°, 315°)四波束的阵列编码图与远场散射结果; (d), (h) $ \left( {{\theta _{{\text{ob}}}}, {\varphi _{{\text{ob}}}}} \right) $分别为(25°, 0°), (25°, 75°), (25°, 150°), (25°, 225°), (25°, 300°)五波束的阵列编码图与远场散射结果
Figure 9. (a), (e) Array coding sequence diagrams and far-field scattering results of $ \left( {{\theta _{{\text{ob}}}}, {\varphi _{{\text{ob}}}}} \right) $ for (20°, 0°) and (20°, 90°) double beams, respectively; (b), (f) array coding sequence diagrams and far-field scattering results of $ \left( {{\theta _{{\text{ob}}}}, {\varphi _{{\text{ob}}}}} \right) $ for (10°, 45°), (20°, 180°) and (25°, 320°) triple beams, respectively; (c), (g) array coding sequence and far-field scattering results of $ \left( {{\theta _{{\text{ob}}}}, {\varphi _{{\text{ob}}}}} \right) $ for (25°, 0°), (30°, 110°), (30°, 220°) and (35°, 315°) four beams, respectively; (d), (h) array coding sequence and far-field scattering results of $ \left( {{\theta _{{\text{ob}}}}, {\varphi _{{\text{ob}}}}} \right) $ for (25°, 0°), (25°, 75°), (25°, 150°), (25°, 225°) and (25°, 300°) five beams, respectively.
图 10 拓扑电荷数分别为$ l = - 1 $, $ l = + 1 $, $ l = - 2 $, $ l = + 2 $的涡旋相位分布图
Figure 10. Diagrams of vortex phase distribution for topological charges $ l = - 1 $, $ l = + 1 $, $ l = - 2 $, $ l = + 2 $ respectively.
图 11 (a)—(d) $ l = \pm 1 $和$ l = \pm 2 $的远场散射图及相位图; (e)—(h) 相对应的模式纯度图
Figure 11. Far-field scattering diagram and phase diagram: (a)–(d) $ l = \pm 1 $ and $ l = \pm 2 $; (e)–(h) the corresponding pattern purity distribution diagrams.
图 12 (a), (b) $ \left( {{\theta _{{\text{ob}}}}, {\varphi _{{\text{ob}}}}} \right) $ 分别为(20°, 120°), (30°, 225°)时的单涡旋波束阵列编码图; (c), (d)对应的三维远场散射图; (e), (f)对应的模式纯度图
Figure 12. (a), (b) Coding diagram of a single vortex beam array at $ \left( {{\theta _{{\text{ob}}}}, {\varphi _{{\text{ob}}}}} \right) $ of (20°, 120°) and (30°, 225°) , respectively; (c), (d) the corresponding three-dimensional far-field scattering diagram; (e), (f) the corresponding model purity diagram.
图 13 (a), (c) $ \left( {{\theta _{{\text{ob}}}}, {\varphi _{{\text{ob}}}}} \right) $分别为(20°, 0°), (20°, 90°)双涡旋波束的阵列编码图及远场散射俯视图; (b), (d) $ \left( {{\theta _{{\text{ob}}}}, {\varphi _{{\text{ob}}}}} \right) $分别为(10°, 45°), (20°, 180°), (25°, 320°)三涡旋波束的阵列编码图及远场散射俯视图
Figure 13. (a), (c) The array coding diagram and the top view of the far-field scattering of $ \left( {{\theta _{{\text{ob}}}}, {\varphi _{{\text{ob}}}}} \right) $ for the (20°, 0°) and (20°, 90°) double-vortex beams, respectively; (b), (d) the array coding diagram and the top view of the far-field scattering of $ \left( {{\theta _{{\text{ob}}}}, {\varphi _{{\text{ob}}}}} \right) $for the (10°, 45°), (20°, 180°) and (25°, 320°) three-vortex beams, respectively.
图 14 编码超表面与同等尺寸的金属板相比RCS缩减图与超表面阵列编码图
Figure 14. RCS reduction plot of the encoded hypersurface compared to a metal plate of the same size with the hypersurface array encoded.
图 15 (a) φ = 0°, (b) φ = 90°时编码超表面和同等尺寸的金属板远场散射图的三维和一维结果对比图
Figure 15. (a) φ = 0°, (b) φ = 90° comparison of three-dimensional and one-dimensional results of the far-field scattering pattern encoding metasurface and metal plate of the same size.
表 1 傅里叶卷积加运算具体规则
Table 1. Specific rules for the Fourier convolutional addition operation.
0
(0°/360°)1
(90°)2
(180°)3
(270°)0
(0°/360°)0 1 2 3 1
(90°)1 2 3 0 2
(180°)2 3 0 1 3
(270°)3 0 1 2 
DownLoad: CSV
-
[1] Davies A G, Linfield E H, Johnston M B 2002 Phys. Med. Biol. 47 3679
Google Scholar
[2] Yu N F, Genevet P, Kats M A, Aieta F, Tetienne J P, Capasso F, Gaburro Z 2011 Science 334 333
Google Scholar
[3] Zhang X Q, Tian Z, Yue W S, Gu J Q, Zhang S, Han J G, Zhang W L 2013 Adv. Mater. 25 4567
Google Scholar
[4] Cui T J, Qi M Q, Wan X, Zhao J, Cheng Q 2014 Light Sci. Appl. 3 e218
Google Scholar
[5] Zhang L, Wu R Y, Bai G D, Wu H T, Mu H T, Ma Q, Chen X Q, Cui T J 2018 Adv. Funct. Mater. 28 1802205
Google Scholar
[6] 黄若彤, 李九生 2023 72 054203
Google Scholar
Huang R T, Li J S 2023 Acta Phys. Sin. 72 054203
Google Scholar
[7] Nie R X, He C H, Zhang R X, Song Z Y 2023 Opt. Laser Technol. 159 109010
Google Scholar
[8] Zhao Y Z, Huang C, Song Z L, Yu C Y, Liang S, Luo X G, Qing A Y 2019 IEEE Access 7 79671
Google Scholar
[9] 李佳辉, 张雅婷, 李吉宁, 李杰, 李继涛, 郑程龙, 杨悦, 黄进, 马珍珍, 马承启, 郝璇若, 姚建铨 2020 69 228101
Google Scholar
Li J H, Zhang Y T, Li J N, Li J, Li J T, Zheng C L, Yang Y, Huang J, Ma Z Z, Ma C Q, Hao X R, Yao J Q 2020 Acta Phys. Sin. 69 228101
Google Scholar
[10] Xiao B G, Zhang Y, Tong S J, Yu J B, Xiao L H 2020 Opt. Express 28 7125
Google Scholar
[11] Jiang C Y, Li Z K, Lv X Y, Tian M, Liu M, Zhang H Y, Zhang Y P 2023 Opt. Commun. 540 129506
Google Scholar
[12] Yang R S, Lou J, Zhang F L, Zhu W, Xu J, Cai T, Fu Q H, Li H, Fan Y C 2021 Adv. Photonics Res. 2 2100103
Google Scholar
[13] Yang R S, Zhang F L, Li Z C, Fu Q H, Fan Y C 2023 Opt. Laser Technol. 163 109380
Google Scholar
[14] Yang R S, Fan Y C, Zhu W, Hu C J, Chen S N, Wei H, Chen W J, Chan C T, Zhao Q, Zhou J, Zhang F L, Qiu C W 2023 Laser Photonics Rev. 17 2200975
Google Scholar
[15] Wu R Y, Shi C B, Liu S, Wu W, Cui T J 2018 Adv. Opt. Mater. 6 1701236
Google Scholar
[16] 张娜, 赵健民, 陈克, 赵俊明, 姜田, 冯一军 2021 70 178102
Google Scholar
Zhang N, Zhao J M, Chen K, Zhao J M, Jiang T, Feng Y J 2021 Acta Phys. Sin. 70 178102
Google Scholar
[17] 贾宇翔, 王甲富, 陈维, 随赛, 朱瑞超, 邱天硕, 李勇峰, 韩亚娟, 屈绍波 2021 雷达学报 10 220
Google Scholar
Jia Y X, Wang J F, Chen W, Sui S, Zhu R C, Qiu T S, Li Y F, Han Y J, Qu S B 2021 J. Radars 10 220
Google Scholar
[18] 韩丁, 马子寅, 王俊林, 王鑫, 刘苏雅拉图 2022 中国激光 49 168
Han D, Ma Z Y, Wang J L, Wang X, Liu S Y L T 2022 Chin. J. Lasers 49 168
[19] Sui S, Ma H, Wang J F, Feng M D, Pang Y Q, Zhang J Q, Xu Z, Qu S B 2019 J. Phys. D: Appl. Phys. 52 035103
Google Scholar
[20] Xiao T, Liu C G, Cheng R S, Cao L F, Tang G P CNSRP Qingdao, China September 24–27, 2023 p4 (in Chinese)[肖彤, 刘成国, 程润生, 曹立锋, 唐光普 第十八届全国电波传播年会 中国青岛 2023年 9月24—27日 第4页]
[21] Kotov O V, Lozovik Y E 2016 Phys. Rev. B 93 235417
Google Scholar
[22] Liu G D, Zhai X, Meng H Y, Lin Q, Huang Y, Zhao C J, Wang L L 2018 Opt. Express 26 11471
Google Scholar
[23] Zhang X G, Tang W X, Jiang W X, Bai G D, Tang J, Bai L, Qiu C W, Cui T J 2018 Adv. Sci. 5 1801028
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 1519
- PDF Downloads: 52
- Cited By: 0
