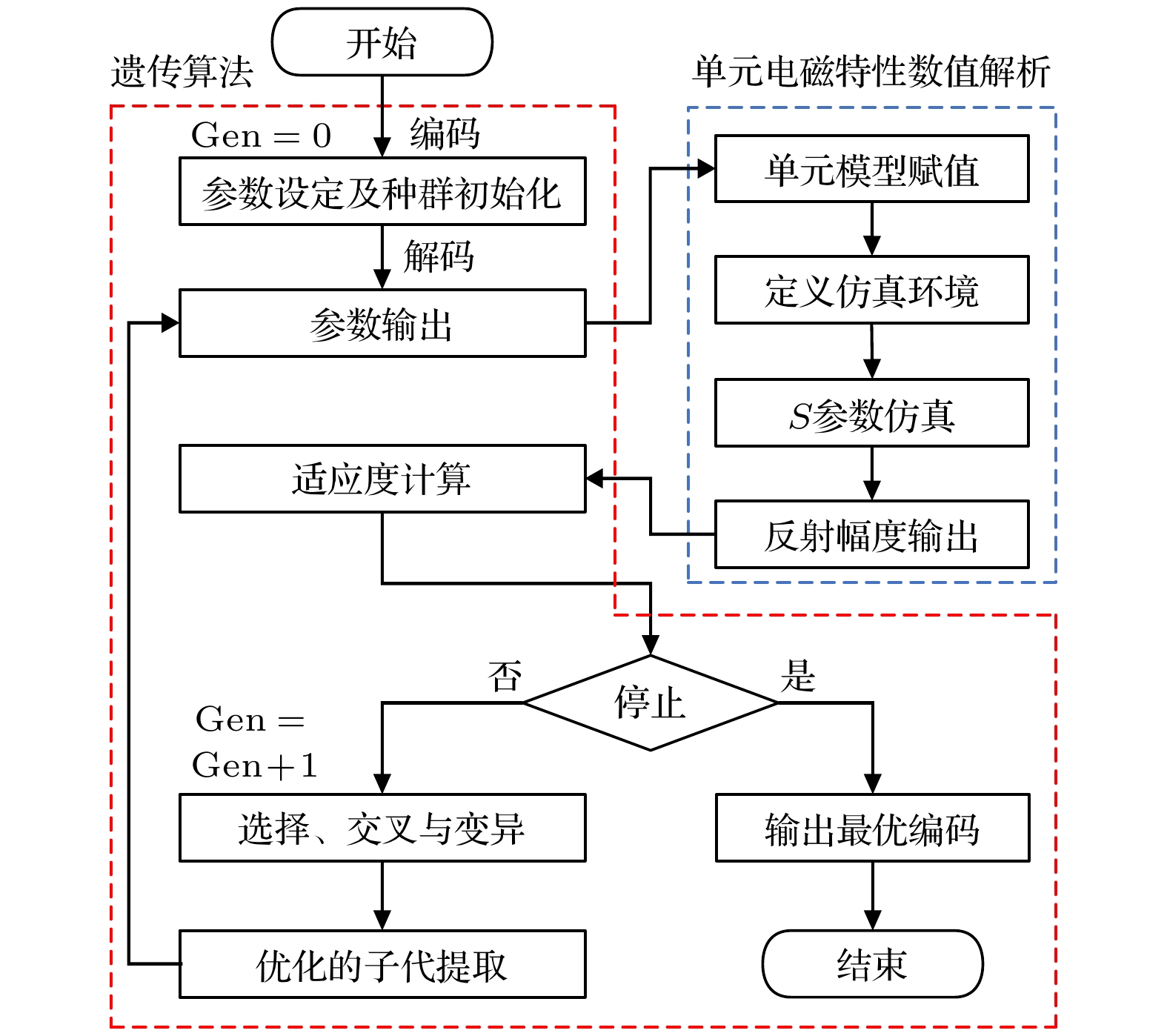
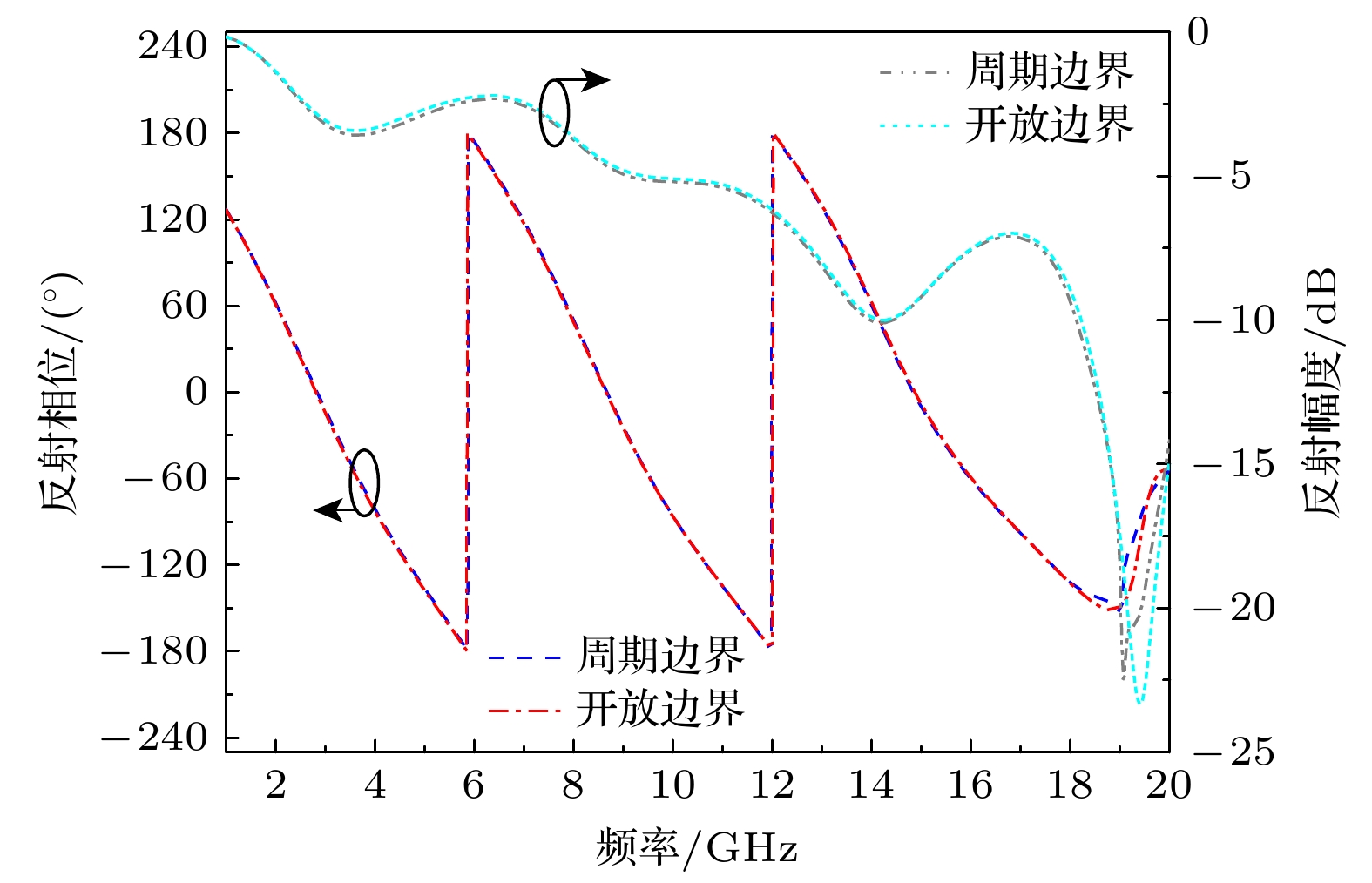
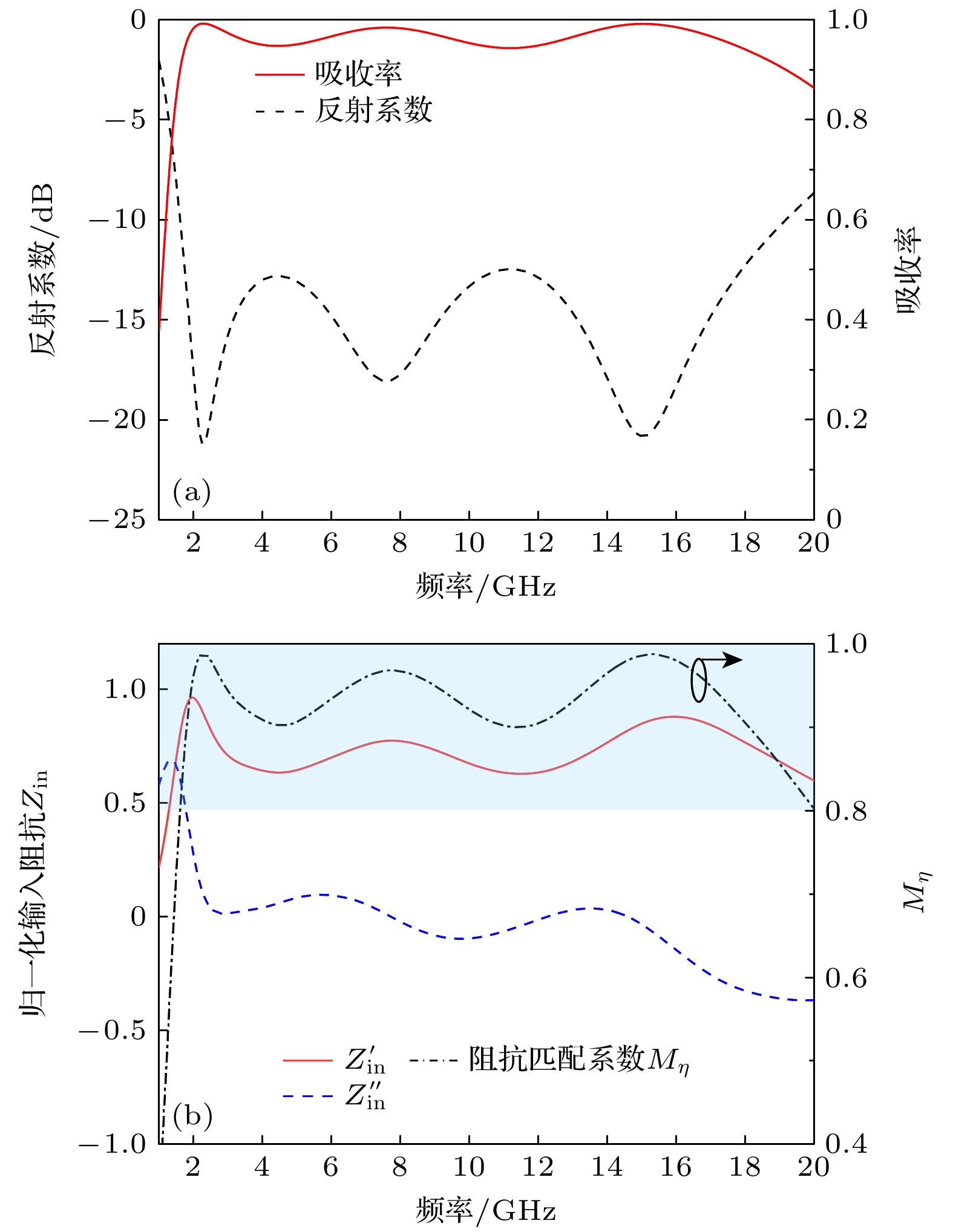
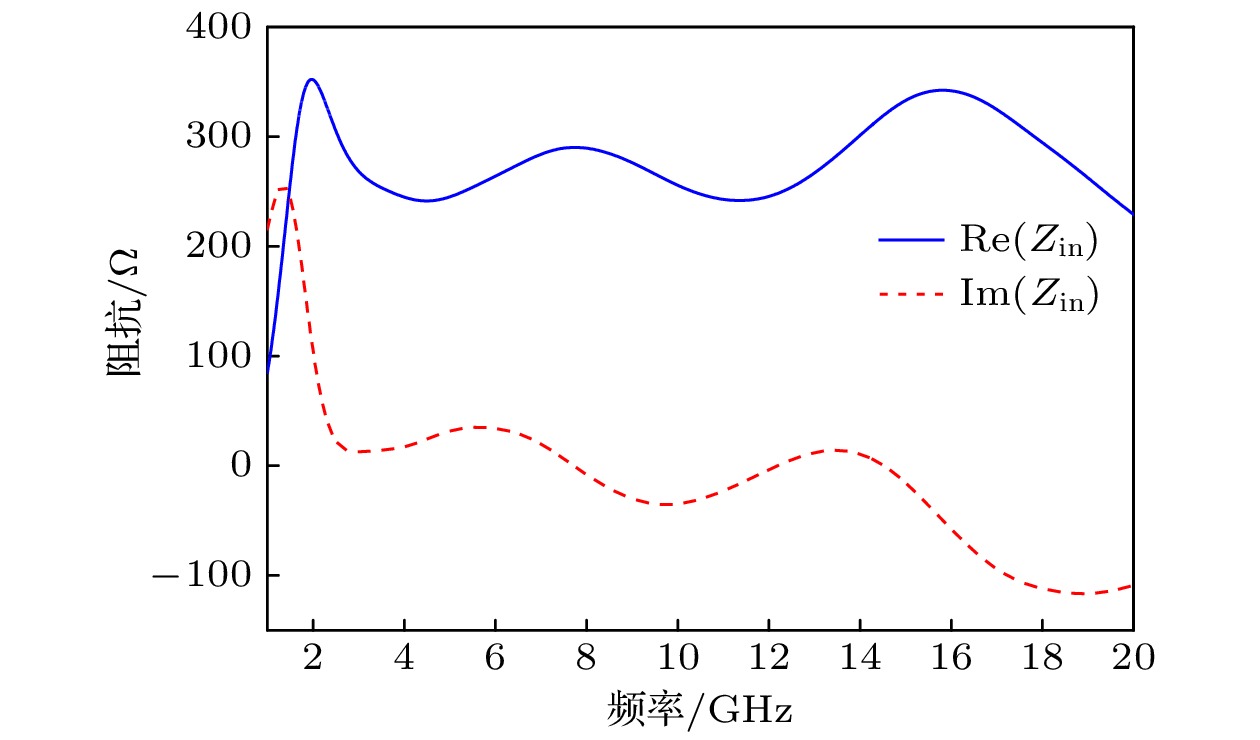
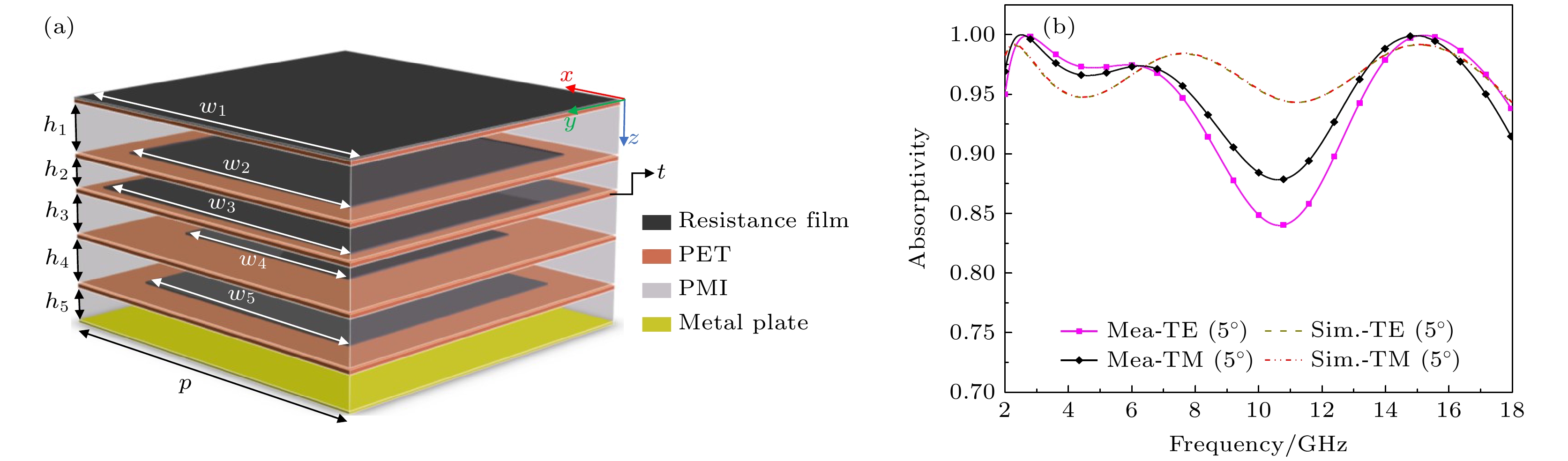
-
近年来, 基于超材料的电磁吸波器件由于其宽带、易制备等优势而备受各国研究者的广泛关注. 本文为实现宽带电磁低可探测, 提出一种渐变电阻膜-介质复合结构的超材料吸波器. 基于传输线理论和阻抗匹配原理, 对强吸波条件进行了分析. 在单元结构设计方面, 采用遗传算法在多变量域内全局搜索最优解, 快速地确定出能够兼顾低频与宽带吸波性能的超材料单元结构与电阻参数, 并对器件吸波性能与吸波机理进行了深入的探讨. 仿真结果表明, 在垂直入射下, 所设计的超材料吸波器对1.62—19.16 GHz (相对带宽168.8%) 之间的入射波吸收率均大于90%, 有效地向L和K波段拓展了吸收带宽. 虽然在部分频段测试和仿真结果之间存在一定偏差, 但两种类型的曲线随频率的变化趋势基本一致, 这充分证明了所设计的超材料吸波器在低频宽带吸波领域具有潜在应用价值.In recent years, electromagnetic (EM) wave absorbing devices based on metamaterials have attracted widespread attention, due to their advantages such as broadband, easy preparation, and flexibility to tailor EM waves. Nevertheless, a review of the existing research reveals that the inherent sub-wavelength characteristics of metamaterials and metasurfaces impose certain constraints on their applications in low-frequency ranges. In order to achieve low detectability that takes into account both low-frequency and broadband absorbing performance, this work, presents a metamaterial absorber based on 5-layer gradient resistance film and dielectric composite structure, as shown in
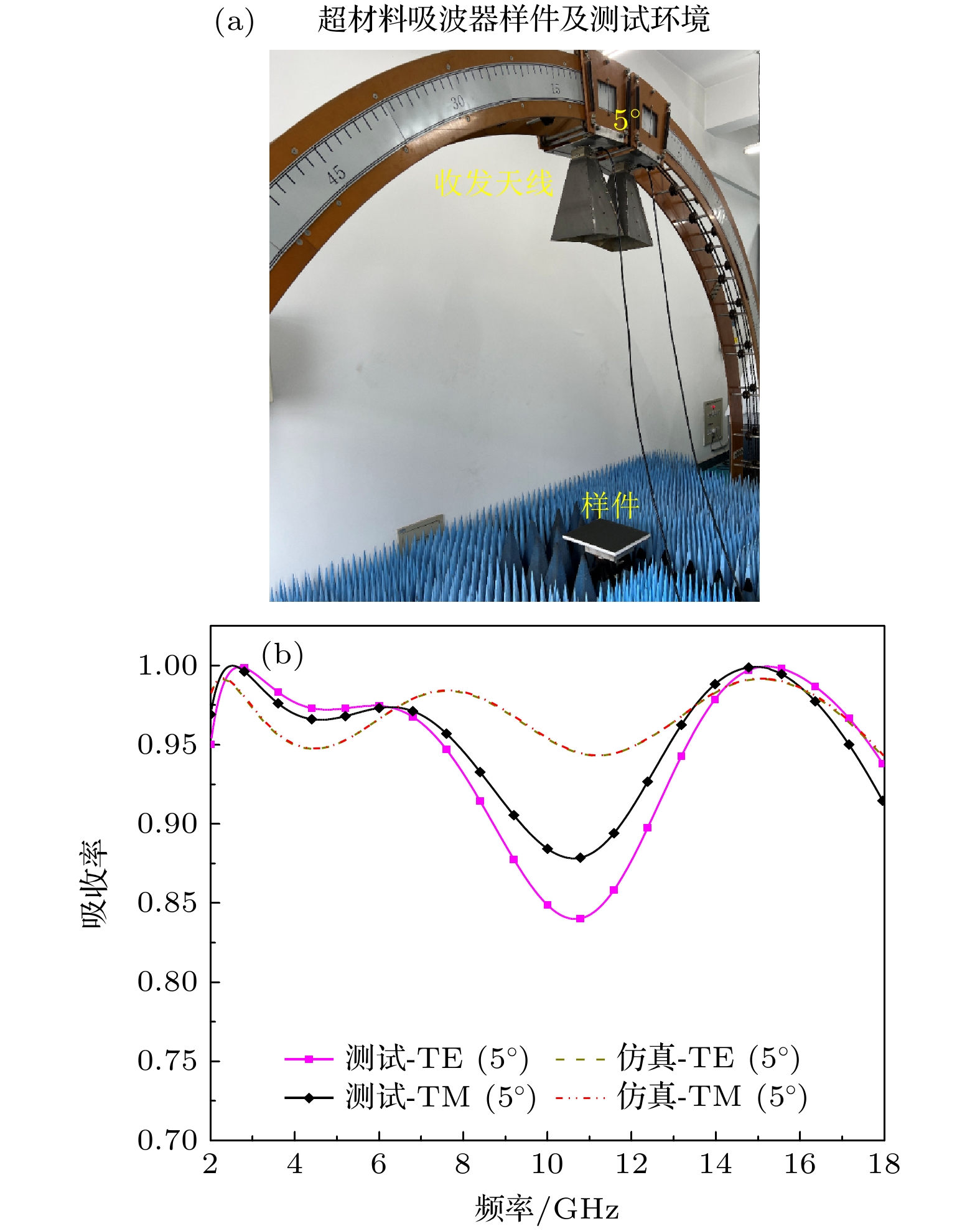
Fig. (a) . To begin with, we introduce the structural design of the initial element, and based on this, the transmission line theory and impedance matching principle are used to analyze the strong wave absorption conditions of the absorber element. In terms of the element structure optimization, the genetic algorithm is adopted to globally search for the optimal solution in the multi-variable domain, resulting in the rapid determination of metamaterial elements’ configurations and resistance parameters that meet the design goals. In the simulation, the wave absorption performance and mechanism of the designed absorbing element are also investigated in an in-depth manner. Simulation results show that the designed metamaterial absorber can achieve more than 90% EM wave absorption in a frequency range of 1.62–19.16 GHz (with a relative bandwidth of 168.8%) under normal incidence of linearly polarized plane waves, which effectively expands the absorption bandwidth to the L band and K band. In addition, the simulations for oblique incidence at different polarizations provide strong evidence for the device’s insensitivity to both polarization and angle. The radar cross section (RCS) curves obtained by the time domain (TD) simulation illustrate that the novel structure can achieve more than 10 dB RCS reduction in a frequency range of 1.7–20 GHz. In the device's performance verification process, a metamaterial absorber with 20 × 20 elements and dimensions of 1.566$ {\lambda }_{l} $ ×1.566$ {\lambda }_{l} $ × 0.113$ {\lambda }_{l} $ is fabricated and tested by using the bow method reflectivity test system. The absorptivity curves under 5° oblique incidence of different polarizations, show that the proposed metamaterial absorber can realize more than 80% EM absorption in an entire frequency range from 2 to 18 GHz, the test results of different polarizations are basically consistent. The test results at oblique incidence (θ ≥ 30°) show that although the measured and simulated curves exhibit discrepancies in certain frequency bands due to human error or material dispersion characteristics, the overall experimental results are consistent with our expectations, which fully proves that the designed metamaterial absorber has potential application value in the field of low-frequency and broadband EM absorption.
-
Keywords:
- metamaterial absorber /
- gadient resistive film /
- genetic algorithm
[1] 汤泽滢, 孙希刚, 程静 2014 航天电子对抗 30 12
Tang Z Y, Sun X G, Cheng J 2014 Aerosp. Electron. Warfare 30 12
[2] 姬金祖, 黄沛霖, 马云鹏, 张生俊 2018 隐身原理 (北京: 北京航空航天大学出版社)
Ji J Z, Huang P L, Ma Y P, Zhang S J 2018 Stealth Principle (Beijing: Bei Hang University Press
[3] 刘顺华, 刘军民, 董星龙, 段玉平 2020 电磁波屏蔽及吸波材料 (北京: 化学工业出版社)
Liu S H, Liu J M, Dong X L, Duan Y P 2020 Electromagnetic Wave Shielding and Absorbing Materials (Beijing: Chemical Industry Press
[4] Zhao H F, Zhao H N, Fang S G, Tang C, Deng L W, Qiu L L, Li C, Du J S, Huang S X 2022 J. Phys. D: Appl. Phys. 55 344003
Google Scholar
[5] 张玉龙, 李萍, 石磊 2018 隐身材料 (北京: 化学工业出版社)
Zhang Y L, Li P, Shi L 2018 Stealth Materials (Beijing: Chemical Industry Press
[6] 王朝辉, 李勇祥, 朱帅 2020 69 234103
Google Scholar
Wang C H, Li Y X, Zhu S 2020 Acta Phys. Sin. 69 234103
Google Scholar
[7] Xiao S Y, Wang T, Liu T T, Zhou C B, Jiang X Y, Zhang J F 2020 J. Phys. D: Appl. Phys. 53 503002
Google Scholar
[8] Ma S H, Li Y G, Zhou J, Zhu Z X 2023 Chin. Phys. Lett. 40 084201
Google Scholar
[9] Zhang R, Ding F, Yuan X J, Chen M J 2022 Chin. Phys. Lett. 39 094101
Google Scholar
[10] Landy N I, Sajuyigbe S, Mock J J, Smith D R, Padilla W J 2008 Phys. Rev. Lett. 100 207402
Google Scholar
[11] Lim D, Lim S 2019 IEEE Antennas Wirel. Propag. Lett. 18 1887
Google Scholar
[12] Zhuang Y Q, Wang G M, Liang J G, Zhang Q F 2017 IEEE Antennas Wirel. Propag. Lett. 16 2606
Google Scholar
[13] 王彦朝, 许河秀, 王朝辉, 王明照, 王少杰 2020 69 134101
Google Scholar
Wang Y Z, Xu H X, Wang C H, Wang M Z, Wang S J 2020 Acta Phys. Sin. 69 134101
Google Scholar
[14] Yang X M, Liu C R, Hou B, Zhou X Y 2021 Chin. Phys. B 30 104102
Google Scholar
[15] Su J X, Li W Y, Qu M J, Yu H, Li Z R, Qi K N, Yin H C 2022 IEEE Trans. Antennas Propag. 70 9415
Google Scholar
[16] 袁方, 毛瑞棋, 高冕, 郑月军, 陈强, 付云起 2022 71 084102
Google Scholar
Yuan F, Mao R Q, Gao M, Zheng Y J, Chen Q, Fu Y Q 2022 Acta Phys. Sin. 71 084102
Google Scholar
[17] Zhao Y T, Chen J Z, Wei Y Q, Zhang C W, Li L, Wu B, Su T 2022 J. Appl. Phys. 131 165108
Google Scholar
[18] 金嘉升, 马成举, 张垚, 张跃斌, 鲍士仟, 李咪, 李东明, 刘洺, 刘芊震, 张贻歆 2023 72 084202
Google Scholar
Jin J S, Ma C J, Zhang Y, Zhang Y B, Bao S Q, Li M, Li D M, Liu M, Liu Q Z, Zhang Y X 2023 Acta Phys. Sin. 72 084202
Google Scholar
[19] Chen P, Kong X L, Han J F, Wang W H, Han K, Ma H Y, Zhao L, Shen X P 2021 Chin. Phys. Lett. 38 027801
Google Scholar
[20] 沈晓鹏, 崔铁军, 叶建祥 2012 61 058101
Google Scholar
Shen X P, Cui T J, Ye J X 2012 Acta Phys. Sin. 61 058101
Google Scholar
[21] Wang C, Wang R Z, Zhang S J, Wang H, Wang W S 2023 J. Appl. Phys. 134 044902
Google Scholar
[22] Ran Y Z, Shi L H, Wang J B, Ma Y, Li J, Liu Y C 2021 J. Appl. Phys. 130 023106
Google Scholar
[23] Chen Q, Sang D, Guo M, Fu Y Q 2018 IEEE Trans. Antennas Propag. 66 4105
Google Scholar
[24] Li S H, Li J S 2019 Chin. Phys. B 28 094210
Google Scholar
[25] 张娜, 赵健民, 陈克, 赵俊明, 姜田, 冯一军 2021 70 178102
Google Scholar
Zhang N, Zhao J M, Chen K, Zhao J M, Jiang T, Feng Y J 2021 Acta Phys. Sin. 70 178102
Google Scholar
[26] Wang C, Wang R Z, An Z L, Liu L Y, Zhou Y S, Tang Z X, Wang W D, Zhang S J 2022 J. Phys. D: Appl. Phys. 55 485001
Google Scholar
[27] Zhang C, Yang J, Yuan W, Zhao J, Dai J Y, Guo T C, Liang J, Xu G Y, Cheng Q, Cui T J 2017 J. Phys. D: Appl. Phys. 50 444002
Google Scholar
[28] 葛宏义, 李丽, 蒋玉英, 李广明, 王飞, 吕明, 张元, 李智 2022 71 108701
Google Scholar
Ge H Y, Li L, Jiang Y Y, Li G M, Wang F, Lü M, Zhang Y, Li Z 2022 Acta Phys. Sin. 71 108701
Google Scholar
[29] Xue W, Zhang J Y, Ma J W, Hou Z L, Zhao Q L, Xie Q, Bi S 2021 J. Phys. D: Appl. Phys. 54 105103
Google Scholar
[30] Li C J, Wang X, Liu X H, Zhang J Y, Bi S, Hou Z L 2023 Carbon 214 118383
Google Scholar
[31] Wu Y J, Lin H, Xiong J, Hou J J, Zhou R, Deng F, Tang R X 2021 J. Appl. Phys. 129 134902
Google Scholar
[32] Zhu W R, Zhao X P, Gong B Y, Liu L H, Su B 2011 Appl. Phys. A 102 147
Google Scholar
[33] Chen J F, Hu Z Y, Wang G D, Huang X T, Wang S M, Hu X W, Liu M H 2015 IEEE Trans. Antennas Propag. 63 4367
Google Scholar
[34] Wang T, He H H, Ding M D, Mao J B, Sun R, Sheng L 2022 Chin. Phys. B 31 037804
Google Scholar
[35] Zhou Q, Yin X W, Ye F, Mo R, Tang Z M, Fan X M, Cheng L F, Zhang L T 2019 Appl. Phys. A 125 131
Google Scholar
-
图 1 基于电阻膜的超材料吸波单元结构及其等效电路模型
Fig. 1. Element configuration and its equivalent circuit model of the proposed resistive film-based metamaterial absorber.
图 2 基于遗传算法的单元结构优化设计流程图
Fig. 2. Flowchart of the element’s configuration optimization design based on the genetic algorithm.
图 3 相同尺寸及电阻参数的单元模型在 “unit cell” 和 “open” 边界下的反射响应
Fig. 3. Reflectance response of the metamaterial absorber with same dimension and resistance parameters under “unit cell” and “open” boundaries.
图 4 垂直入射时超材料吸波单元的反射系数、吸收率(a)和归一化输入阻抗和阻抗匹配系数(b)随频率变化曲线
Fig. 4. Reflection coefficient, absorption (a), normalized input impedance and impedance matching coefficient (b) versus frequency curves of the designed metamaterial absorber element under normal incidence of linearly polarized waves.
图 5 不同极化的电磁波斜入射下, 超材料吸波单元的反射系数和吸收率随频率变化曲线 (a), (b) 反射系数; (c), (d) 吸收率; (e) 垂直入射时, 吸收率对极化角的依赖关系; (f) 吸收率对入射角的依赖关系
Fig. 5. Reflection coefficient and absorption curves of the proposed metamaterial absorber under the oblique incidence of electromagnetic waves with different polarizations: (a), (b) Reflection coefficients; (c), (d) absorptivity; (e) dependence of absorptivity on polarization angle at normal incidence; (f) dependence of absorptivity on angle of incidence.
图 6 电阻膜(a), (b)及PET膜(c), (d)上的能量损耗分布图 (a), (c) 4 GHz, (b), (d) 7.6 GHz
Fig. 6. Power loss distribution on the resistive film (a), (b) and the PET film (c), (d): (a), (c) 4 GHz, (b), (d) 7.6 GHz.
图 7 (a) 超材料吸波阵列三维模型示意图; (b) 有限阵列与无限阵列的反射系数仿真结果
Fig. 7. (a) Schematic diagram of three-dimensional model of the proposed metamaterial absorbing array; (b) comparison of the simulated results of reflection coefficients for finite and infinite arrays.
图 8 超材料吸波阵列表面输入阻抗随频率的变化曲线
Fig. 8. Variation curves of surface input impedance of metamaterial absorber with frequency.
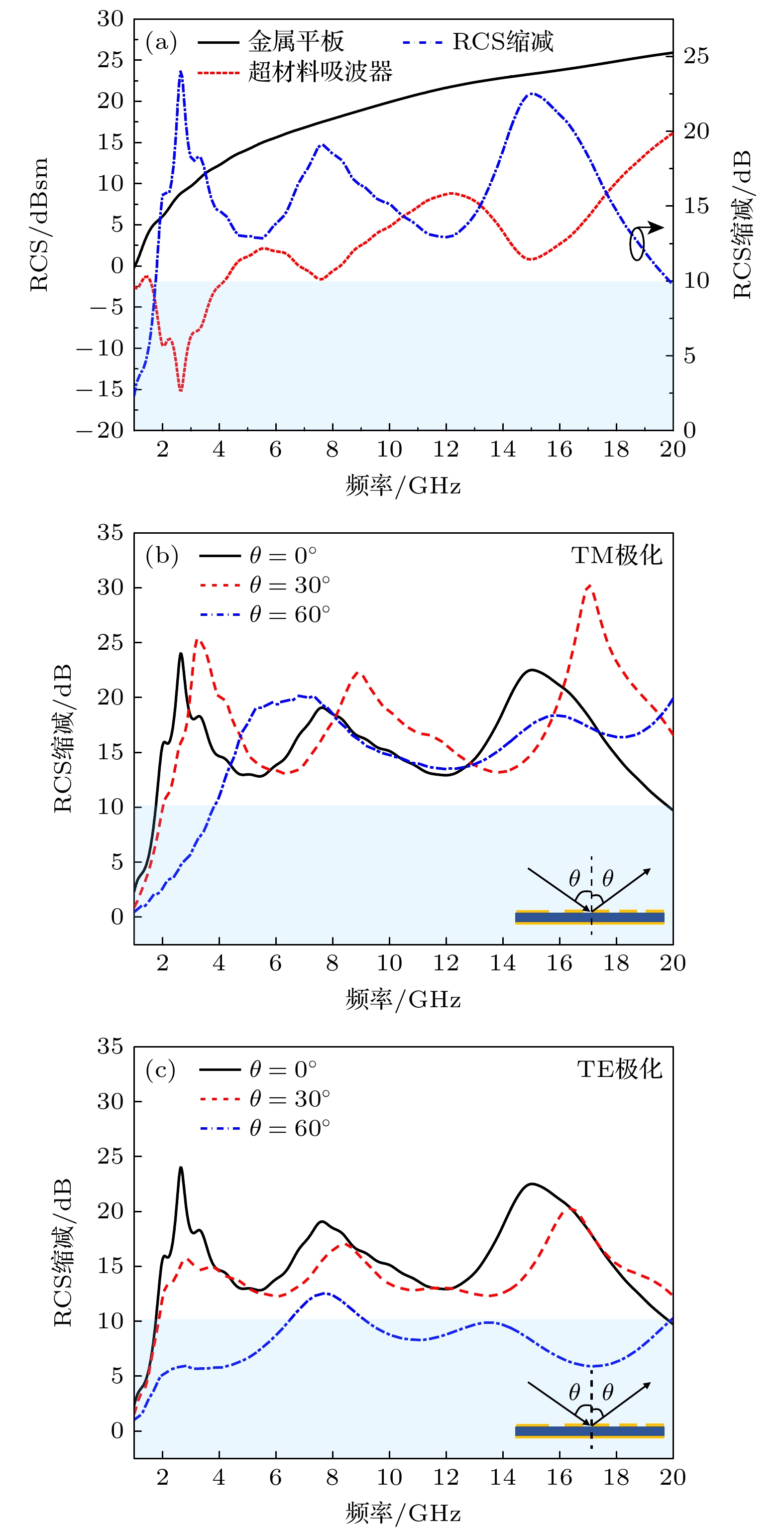
图 9 (a) TM极化波垂直入射时, 超材料吸波阵列的RCS仿真结果. (b), (c) 不同极化的电磁波斜入射时, 吸波器的RCS减缩性能仿真结果 (b) TM极化; (c) TE极化
Fig. 9. (a) Simulated RCS curves of the metamaterial absorber under the normal incidence of TM-polarized wave. (b), (c) RCS reduction performance of the proposed metamaterial absorber under oblique incidence of different polarizations: (b) TM polarization; (c) TE polarization.
图 10 (a) 超材料吸波器样件及测试环境; (b) 所设计的超材料吸波器在不同极化的电磁波5° 斜入射时, 吸收率测试和仿真结果
Fig. 10. (a) Photographs of the fabricated prototype and its measurement setup; (b) the measured and simulated results of absorption rate for the proposed metamaterial absorber under 5° oblique incidence of different polarizations.
图 11 不同入射角度的TM和TE极化电磁波斜入射时超材料吸波器的吸收率测试和仿真结果对比 (a) θ = 30°; (b) θ = 60°
Fig. 11. Comparison of measured and simulated results for the designed metamaterial absorber under oblique incidence of TM- and TE-polarized electromagnetic waves: (a) θ = 30°; (b) θ = 60°.
表 1 具有最优吸波性能的超材料单元参数
Table 1. Metamaterial element parameters with optimal wave absorption performance.
可变参数 固定尺寸参数/mm $ {h}_{1} $—$ {h}_{5} $/mm 4.0 4.7 3.0 3.7 1.5 p 14.5 $ {w}_{1}—{w}_{5} $/mm 11.0 12.0 13.5 13.0 14.5 t 0.8 $ {R}_{1}—{R}_{5} $/(Ω·square–1) 500 450 345 335 250 — — 
下载: 导出CSV
表 2 本文工作与其他宽带超材料吸波器的性能对比结果
Table 2. Comparison of the wave absorption performance between this study and other broadband metamaterial absorbers.
文献/年 厚度/${\lambda }_{l} $ 90% 吸波带宽GHz (FBW) 角度稳定性 仿真 测试 [34]/2022 0.118 10.47—45.44 (125.1%) < 55° [31]/2021 0.098 3.21—14.35 (126.88%) 3.20—14.36 (127.1%) < 45° [35]/2019 0.120 8—18 (71.4%) < 30° [33]/2015 0.230 3.65—13.93 (117%) (80%)吸波 3.85—13.00 (108.6%) < 45° 本文工作 0.113 1.62—19.16 (168.8%) TM: 2—9.5 (131%); 11.6—18 (43%)
TE: 2—8.8 (126%); 12.4—18 (37%)< 45°
下载: 导出CSV
-
[1] 汤泽滢, 孙希刚, 程静 2014 航天电子对抗 30 12
Tang Z Y, Sun X G, Cheng J 2014 Aerosp. Electron. Warfare 30 12
[2] 姬金祖, 黄沛霖, 马云鹏, 张生俊 2018 隐身原理 (北京: 北京航空航天大学出版社)
Ji J Z, Huang P L, Ma Y P, Zhang S J 2018 Stealth Principle (Beijing: Bei Hang University Press
[3] 刘顺华, 刘军民, 董星龙, 段玉平 2020 电磁波屏蔽及吸波材料 (北京: 化学工业出版社)
Liu S H, Liu J M, Dong X L, Duan Y P 2020 Electromagnetic Wave Shielding and Absorbing Materials (Beijing: Chemical Industry Press
[4] Zhao H F, Zhao H N, Fang S G, Tang C, Deng L W, Qiu L L, Li C, Du J S, Huang S X 2022 J. Phys. D: Appl. Phys. 55 344003
Google Scholar
[5] 张玉龙, 李萍, 石磊 2018 隐身材料 (北京: 化学工业出版社)
Zhang Y L, Li P, Shi L 2018 Stealth Materials (Beijing: Chemical Industry Press
[6] 王朝辉, 李勇祥, 朱帅 2020 69 234103
Google Scholar
Wang C H, Li Y X, Zhu S 2020 Acta Phys. Sin. 69 234103
Google Scholar
[7] Xiao S Y, Wang T, Liu T T, Zhou C B, Jiang X Y, Zhang J F 2020 J. Phys. D: Appl. Phys. 53 503002
Google Scholar
[8] Ma S H, Li Y G, Zhou J, Zhu Z X 2023 Chin. Phys. Lett. 40 084201
Google Scholar
[9] Zhang R, Ding F, Yuan X J, Chen M J 2022 Chin. Phys. Lett. 39 094101
Google Scholar
[10] Landy N I, Sajuyigbe S, Mock J J, Smith D R, Padilla W J 2008 Phys. Rev. Lett. 100 207402
Google Scholar
[11] Lim D, Lim S 2019 IEEE Antennas Wirel. Propag. Lett. 18 1887
Google Scholar
[12] Zhuang Y Q, Wang G M, Liang J G, Zhang Q F 2017 IEEE Antennas Wirel. Propag. Lett. 16 2606
Google Scholar
[13] 王彦朝, 许河秀, 王朝辉, 王明照, 王少杰 2020 69 134101
Google Scholar
Wang Y Z, Xu H X, Wang C H, Wang M Z, Wang S J 2020 Acta Phys. Sin. 69 134101
Google Scholar
[14] Yang X M, Liu C R, Hou B, Zhou X Y 2021 Chin. Phys. B 30 104102
Google Scholar
[15] Su J X, Li W Y, Qu M J, Yu H, Li Z R, Qi K N, Yin H C 2022 IEEE Trans. Antennas Propag. 70 9415
Google Scholar
[16] 袁方, 毛瑞棋, 高冕, 郑月军, 陈强, 付云起 2022 71 084102
Google Scholar
Yuan F, Mao R Q, Gao M, Zheng Y J, Chen Q, Fu Y Q 2022 Acta Phys. Sin. 71 084102
Google Scholar
[17] Zhao Y T, Chen J Z, Wei Y Q, Zhang C W, Li L, Wu B, Su T 2022 J. Appl. Phys. 131 165108
Google Scholar
[18] 金嘉升, 马成举, 张垚, 张跃斌, 鲍士仟, 李咪, 李东明, 刘洺, 刘芊震, 张贻歆 2023 72 084202
Google Scholar
Jin J S, Ma C J, Zhang Y, Zhang Y B, Bao S Q, Li M, Li D M, Liu M, Liu Q Z, Zhang Y X 2023 Acta Phys. Sin. 72 084202
Google Scholar
[19] Chen P, Kong X L, Han J F, Wang W H, Han K, Ma H Y, Zhao L, Shen X P 2021 Chin. Phys. Lett. 38 027801
Google Scholar
[20] 沈晓鹏, 崔铁军, 叶建祥 2012 61 058101
Google Scholar
Shen X P, Cui T J, Ye J X 2012 Acta Phys. Sin. 61 058101
Google Scholar
[21] Wang C, Wang R Z, Zhang S J, Wang H, Wang W S 2023 J. Appl. Phys. 134 044902
Google Scholar
[22] Ran Y Z, Shi L H, Wang J B, Ma Y, Li J, Liu Y C 2021 J. Appl. Phys. 130 023106
Google Scholar
[23] Chen Q, Sang D, Guo M, Fu Y Q 2018 IEEE Trans. Antennas Propag. 66 4105
Google Scholar
[24] Li S H, Li J S 2019 Chin. Phys. B 28 094210
Google Scholar
[25] 张娜, 赵健民, 陈克, 赵俊明, 姜田, 冯一军 2021 70 178102
Google Scholar
Zhang N, Zhao J M, Chen K, Zhao J M, Jiang T, Feng Y J 2021 Acta Phys. Sin. 70 178102
Google Scholar
[26] Wang C, Wang R Z, An Z L, Liu L Y, Zhou Y S, Tang Z X, Wang W D, Zhang S J 2022 J. Phys. D: Appl. Phys. 55 485001
Google Scholar
[27] Zhang C, Yang J, Yuan W, Zhao J, Dai J Y, Guo T C, Liang J, Xu G Y, Cheng Q, Cui T J 2017 J. Phys. D: Appl. Phys. 50 444002
Google Scholar
[28] 葛宏义, 李丽, 蒋玉英, 李广明, 王飞, 吕明, 张元, 李智 2022 71 108701
Google Scholar
Ge H Y, Li L, Jiang Y Y, Li G M, Wang F, Lü M, Zhang Y, Li Z 2022 Acta Phys. Sin. 71 108701
Google Scholar
[29] Xue W, Zhang J Y, Ma J W, Hou Z L, Zhao Q L, Xie Q, Bi S 2021 J. Phys. D: Appl. Phys. 54 105103
Google Scholar
[30] Li C J, Wang X, Liu X H, Zhang J Y, Bi S, Hou Z L 2023 Carbon 214 118383
Google Scholar
[31] Wu Y J, Lin H, Xiong J, Hou J J, Zhou R, Deng F, Tang R X 2021 J. Appl. Phys. 129 134902
Google Scholar
[32] Zhu W R, Zhao X P, Gong B Y, Liu L H, Su B 2011 Appl. Phys. A 102 147
Google Scholar
[33] Chen J F, Hu Z Y, Wang G D, Huang X T, Wang S M, Hu X W, Liu M H 2015 IEEE Trans. Antennas Propag. 63 4367
Google Scholar
[34] Wang T, He H H, Ding M D, Mao J B, Sun R, Sheng L 2022 Chin. Phys. B 31 037804
Google Scholar
[35] Zhou Q, Yin X W, Ye F, Mo R, Tang Z M, Fan X M, Cheng L F, Zhang L T 2019 Appl. Phys. A 125 131
Google Scholar
下载:
计量
- 文章访问数: 2139
- PDF下载量: 86
- 被引次数: 0
