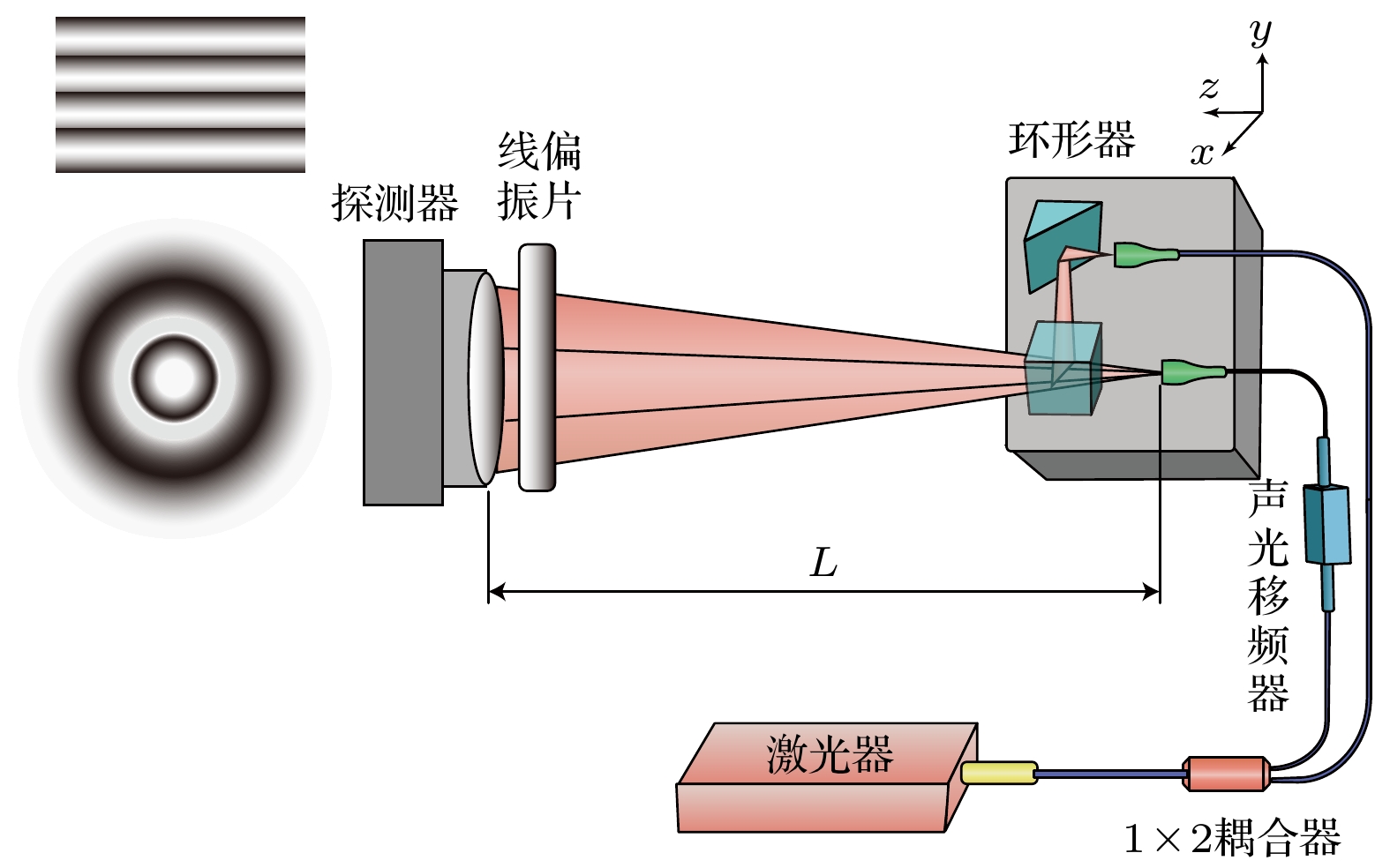
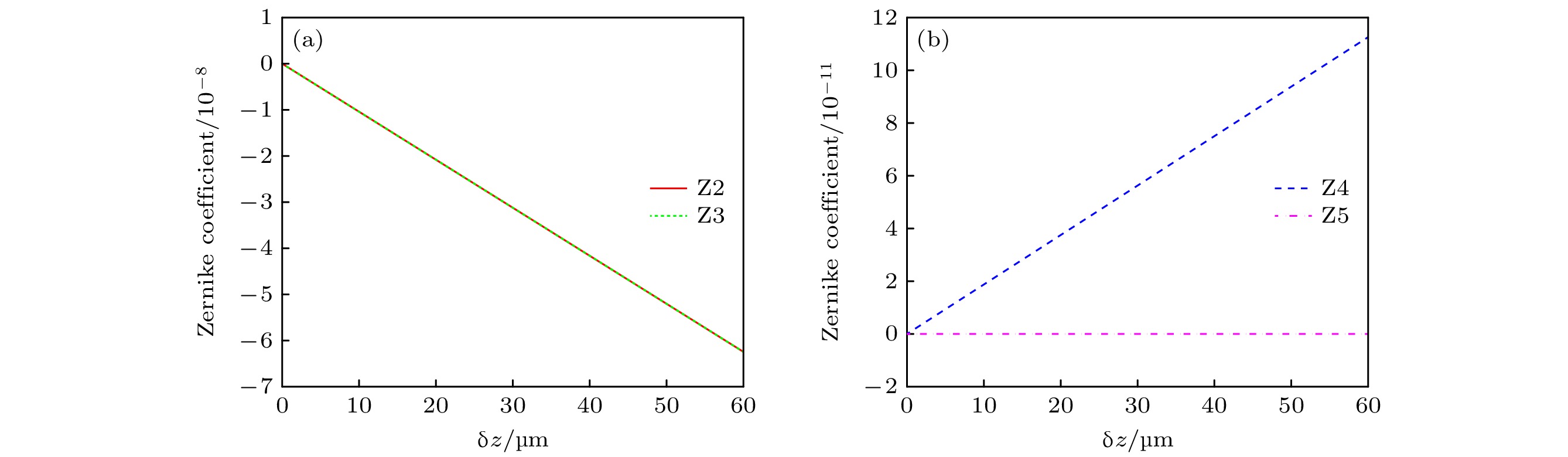
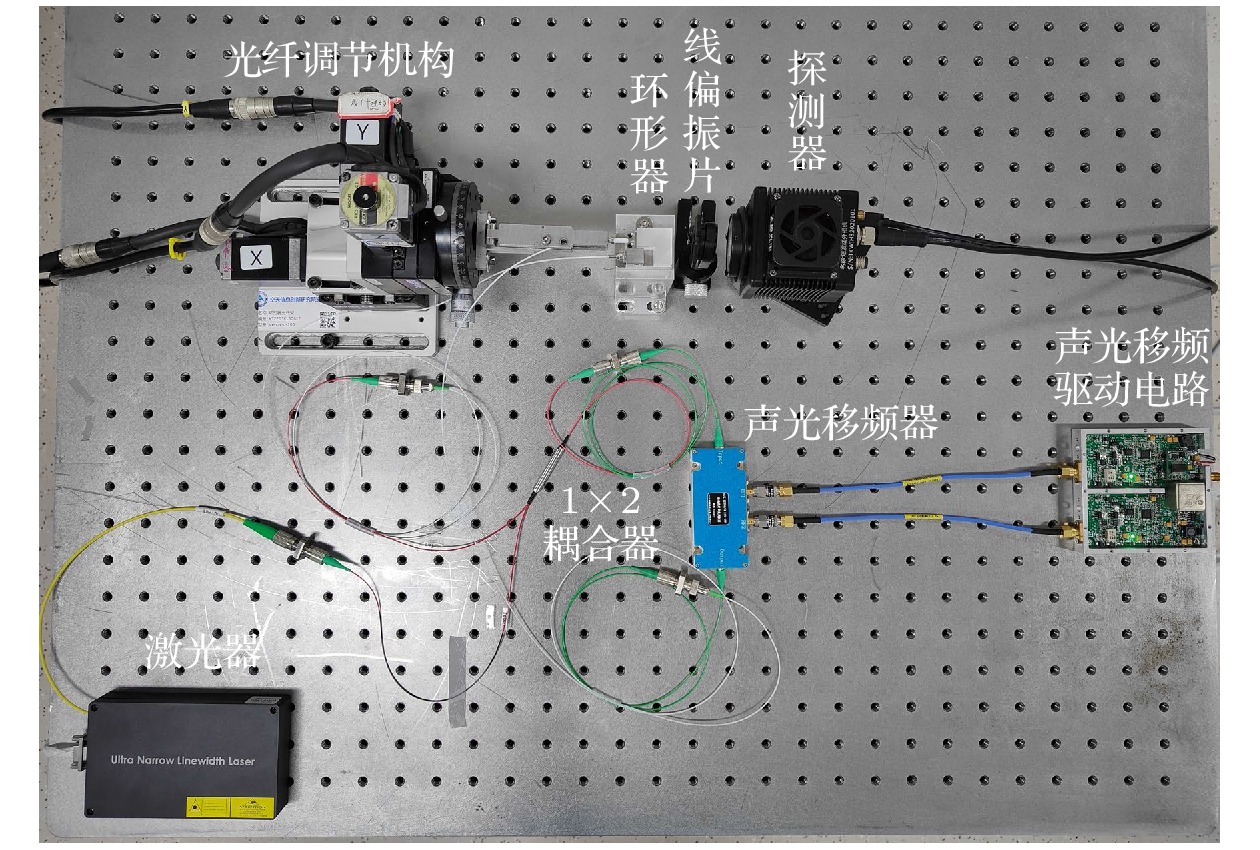
-
The fiber optic circulator in the form of point diffraction is a key component for coupling fiber optical path and spatial optical path in a laser Doppler vibration measurement system. The coupling efficiency and other performance parameters of fiber optic circulator are great significant for improving measurement accuracy and working distance of vibration measurement system. The conventional circulator coincidence detection methods include energy monitoring method and far-field coincidence monitoring method, which cannot be used to quantitatively analyze the fiber mismatch factors. Therefore, the consistency of the circulator coupling efficiency cannot be guaranteed. To solve these problems, a phase detection technology based on Hertz-level frequency-shifting heterodyne interferometry is proposed. The interferometry phase information is used to calculate the relative spatial positions of optical fibers, and this technology performs quantitative detection in the fiber alignment process. The interference wavefront formed by relative spatial positions of optical fibers is simulated and validated experimentally. The curves of coupling efficiency and wavefront PV value versus different kinds of alignment errors are simulated and analyzed. By fitting the interference wavefront with the Zernike polynomials, the correspondence between different kinds of alignment errors and Zernike coefficients is obtained. The value of Z2 (Zernike coefficient) can be used as the basis for judging whether there is transverse displacement in the Y direction. Similarly, Z3 corresponds to the transverse displacement in the X direction, Z4 corresponds to the longitudinal displacement in the Z direction and Z5 corresponds to the optical axis angle. Through this correspondence relationship, the quantitative separation and analysis of fiber mismatch factors are realized. The experimental results show that the accuracy of this method for measuring lateral displacement is better than 1μm. According to the phase diagram obtained from the experiment, Zernike coefficient fitting is performed. The lateral displacement deviation, longitudinal displacement deviation, and angular deviation are calculated by the coefficients of Z2 to Z5. The fiber adjustment mechanism corrects the transverse displacement deviation. It provides a new detection method for realizing fiber alignment and mismatch correction. Compared with the existing detection methods, the phase detection method based on Hertz-level frequency-shifting heterodyne interferometry solves the quantification problem of fiber coincidence adjustment. This method has the advantages of high measurement accuracy, compact detection structure and composition, and low detection cost. This method has great potential applications in the fields of optical fiber and spatial optical device alignment, optical system aberration detection, and planar wavefront detection.
-
Keywords:
- fiber mismatch /
- alignment error /
- heterodyne interferometry /
- coupling efficiency
[1] 张琦, 王洪斌, 姜睿, 杜传宇 2022 航空发动机 48 76
Zhang Q, Wang H B, Jiang R, Du C Y 2022 Aeroengine 48 76
[2] Fu X, Liu Y Q, Hu X D, Li D C, Hu X T 2004 J. Optoelectron. Laser 11 1357
[3] Ebert R, Lutzmann P, Hebel M 2008 IEEE Photonics Global Singapore, 2008, p1
[4] Zhu Z, Li W, Molina E, Wolberg G 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 2007 p1
[5] 张文 2016 博士学位论文(杭州: 浙江大学)
Zhang W 2016 Ph. D. Dissertation (Hangzhou: Zhejiang University
[6] 刘爱东, 于梅 2015 振动与冲击 34 212
Liu A D, Yu M 2015 J. Vib. Shock 34 212
[7] 吕韬 2019 博士学位论文(长春: 中国科学院长春光学精密机械与物理研究所)
Lv T 2019 Ph. D. Dissertation (Changchun: Chinese Academy of Sciences Changchun Institute of Optics Fine Mechanics and Physics
[8] Li R, Poulos N M, Zhu Z G, Xie L P 2012 Appl. Opt. 51 5011
Google Scholar
[9] Han X Y, Lv T, Wu S S, Li Y Y, He B 2019 Opt. Laser Technol. 111 575
Google Scholar
[10] He Q, Zhao Z G, Ye X D, Luo C, Zhang D C, Wang S F, Xu X P 2022 Micromachines 13 324
Google Scholar
[11] Alaruri S D 2015 Optik 126 5923
Google Scholar
[12] Liu X Y, Guo J, Li G N, Chen N, Shi K 2019 Results Phys. 12 1044
Google Scholar
[13] Zhang M Q, Zhi D, Chang Q, Ma P F, Ma Y X, Su R T, Wu J, Zhou P, Si L 2019 Laser Phys. 29 115101
Google Scholar
[14] Yan Y X, Zheng Y, Duan J A, Huang Z L 2020 Opt. Fiber Technol. 58 102301
Google Scholar
[15] Phattaraworamet T, Saktioto T, Ali J, Fadhali M, Yupapin P P, Zainal J, Mitatha S 2010 Optik 121 2240
Google Scholar
[16] 丁莉, 刘代中, 高妍琦, 朱宝强, 朱俭, 彭增云, 朱健强, 俞立钧 2008 57 5713
Google Scholar
Ding L, Liu D Z, Gao Y Q, Zhu B Q, Zhu J, Peng Z Y, Zhu J Q, Yu L J 2008 Acta Phys. Sin. 57 5713
Google Scholar
[17] 陶嘉庆, 胡越, 项华中, 涂建坤, 郑刚 2021 电子科技 34 37
Google Scholar
Tao J Q, Hu Y, Xiang Z H, Tu J K, Zheng G 2021 Electron. Sci. Technol. 34 37
Google Scholar
[18] Zhu M X, Bai F Z, Gan S M, Huang K Z, Huang L H, Wang J X 2013 Optik 124 5624
Google Scholar
[19] Wallner O, Winzer P J, Leeb W R 2002 Appl. Opt. 41 637
Google Scholar
[20] Kang J M, Guo P, Zhang Y C, Chen H, Chen S Y, Ge X Y 2013 SPIE Fifth International Symposium on Photoelectronic Detection and Imaging Beijing, China, June 25, 2013 p891417
-
图 1 多普勒测振系统及光纤环形器示意图 (a)光纤M-Z式激光相干多普勒测振系统示意图; (b) 光纤环形器示意图
Figure 1. Schematic diagrams of laser Doppler vibration measurement system and fiber circulator: (a) Schematic diagrams of fiber M-Z laser coherent Doppler vibration measurement system; (b) schematic diagram of fiber circulator.
图 2 光纤相对姿态示意图 (a) 横向位移; (b) 纵向位移; (c) 光轴倾斜
Figure 2. Schematic diagram of relative position of optical fibers: (a) Transverse displacement; (b) longitudinal displacement; (c) the optical axis tilts around the X-axis.
图 3 检测系统原理图
Figure 3. Schematic diagram of detection system.
图 4 横向位移与耦合效率和波前PV值关系曲线 (a) X方向横向位移; (b) Y方向横向位移
Figure 4. The curves of coupling efficiency and wavefront PV value versus transverse displacement: (a) X-direction transverse displacement; (b) Y-direction transverse displacement.
图 5 纵向位移(Z方向)与耦合效率和波前PV值关系曲线
Figure 5. The curves of coupling efficiency and wavefront PV value versus longitudinal displacement (Z-direction).
图 6 光轴夹角(绕X轴旋转)与耦合效率和波前PV值关系曲线
Figure 6. The curves of coupling efficiency and wavefront PV value versus optical axis angle (rotation about X-axis).
图 7 光纤相对姿态不同因素同时存在时干涉图和相位图 (a) 干涉图; (b)相位图
Figure 7. Interferogram and phase diagram of optical fibers with different kinds of alignment errors co-existing: (a) Interferogram; (b) phase diagram.
图 8 横向位移(X方向)与Zernike系数关系曲线
Figure 8. The curves of Zernike coefficiencts versus transverse displacement (X-direction).
图 9 横向位移(Y方向)与Zernike系数关系曲线
Figure 9. The curves of Zernike coefficiencts versus transverse displacement (Y-direction).
图 11 光轴夹角(绕X轴旋转)与Zernike系数关系曲线 (a) Z2曲线; (b) Z3曲线; (c) Z4曲线; (d) Z5曲线
Figure 11. The curves of Zernike coefficiencts versus optical axis angle (rotation about X-axis): (a) Z2 vs. angle; (b) Z3 vs. angle; (c) Z4 vs. angle; (d) Z5 vs. angle.
图 10 纵向位移(Z方向)与Zernike系数关系曲线 (a) Z2和Z3曲线; (b) Z4和Z5曲线
Figure 10. The curves of Zernike coefficiencts versus longitudinal displacement (Z-direction): (a) Z2 and Z3 vs. Z displacement; (b) Z4 and Z5 vs. Z displacement.
图 12 实验装置图
Figure 12. Diagram of the experimental setup.
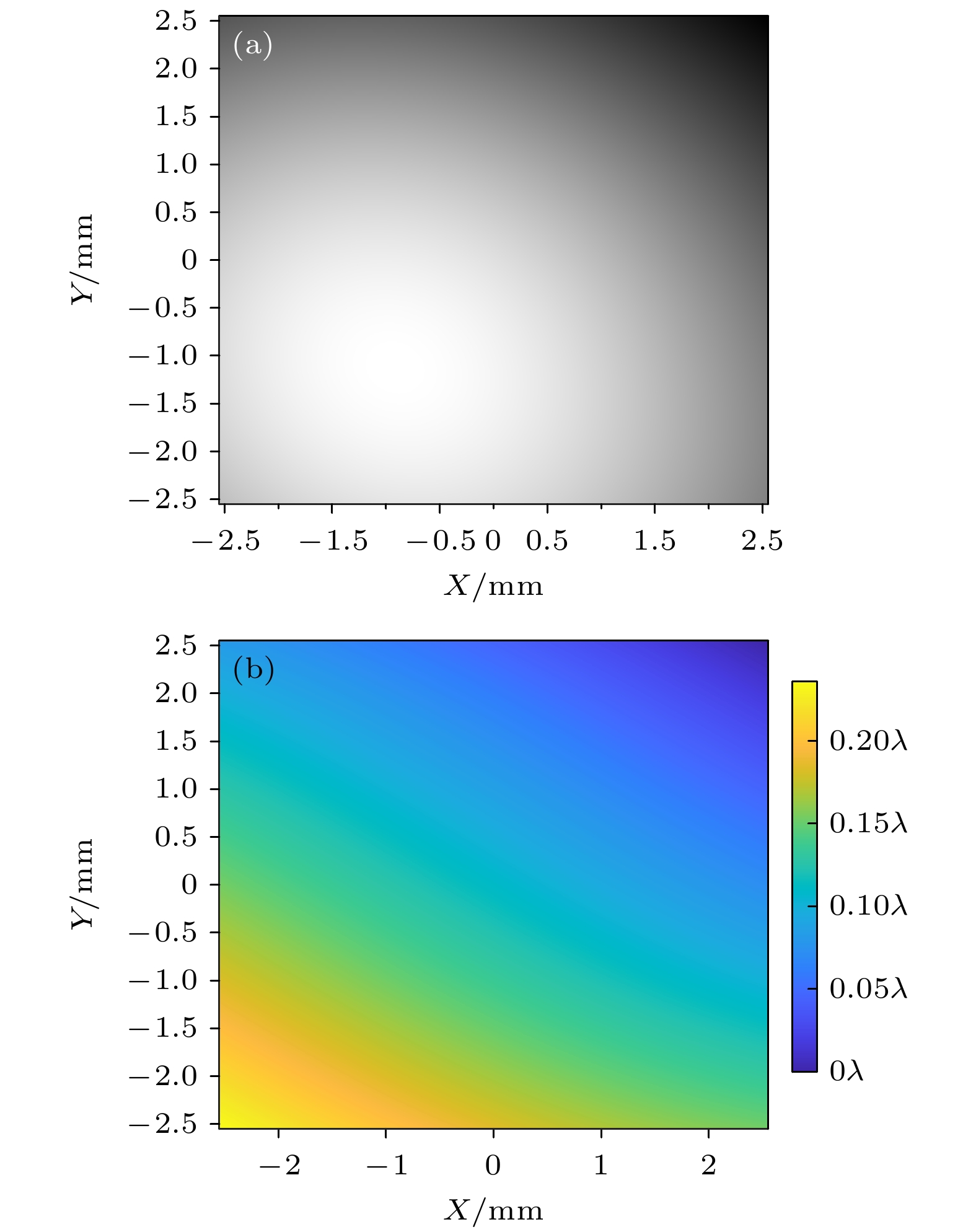
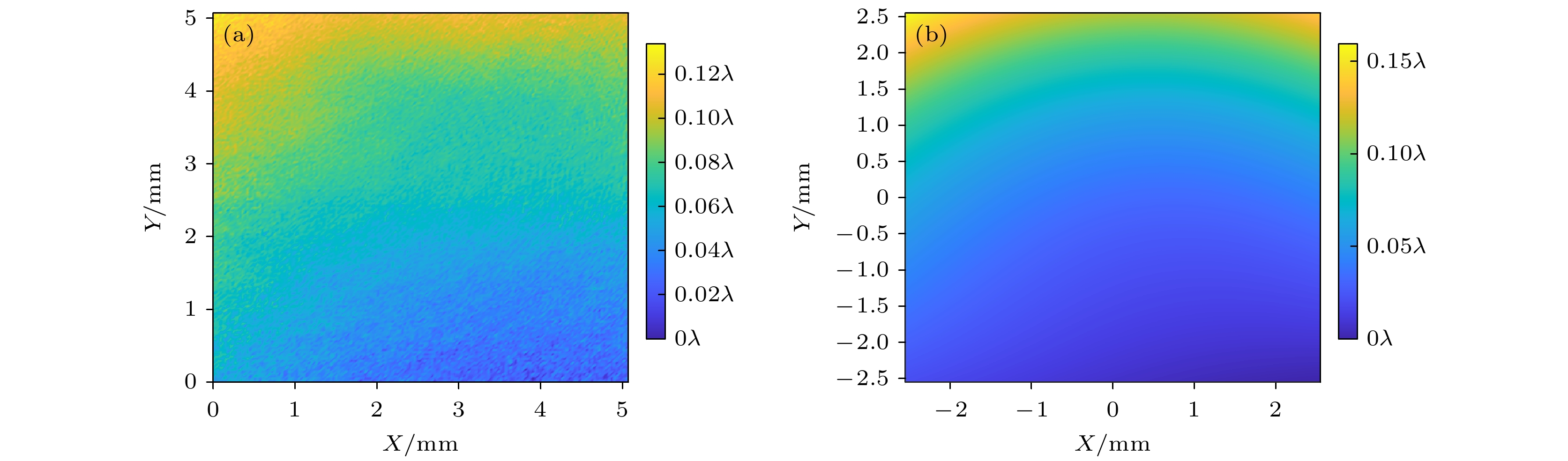
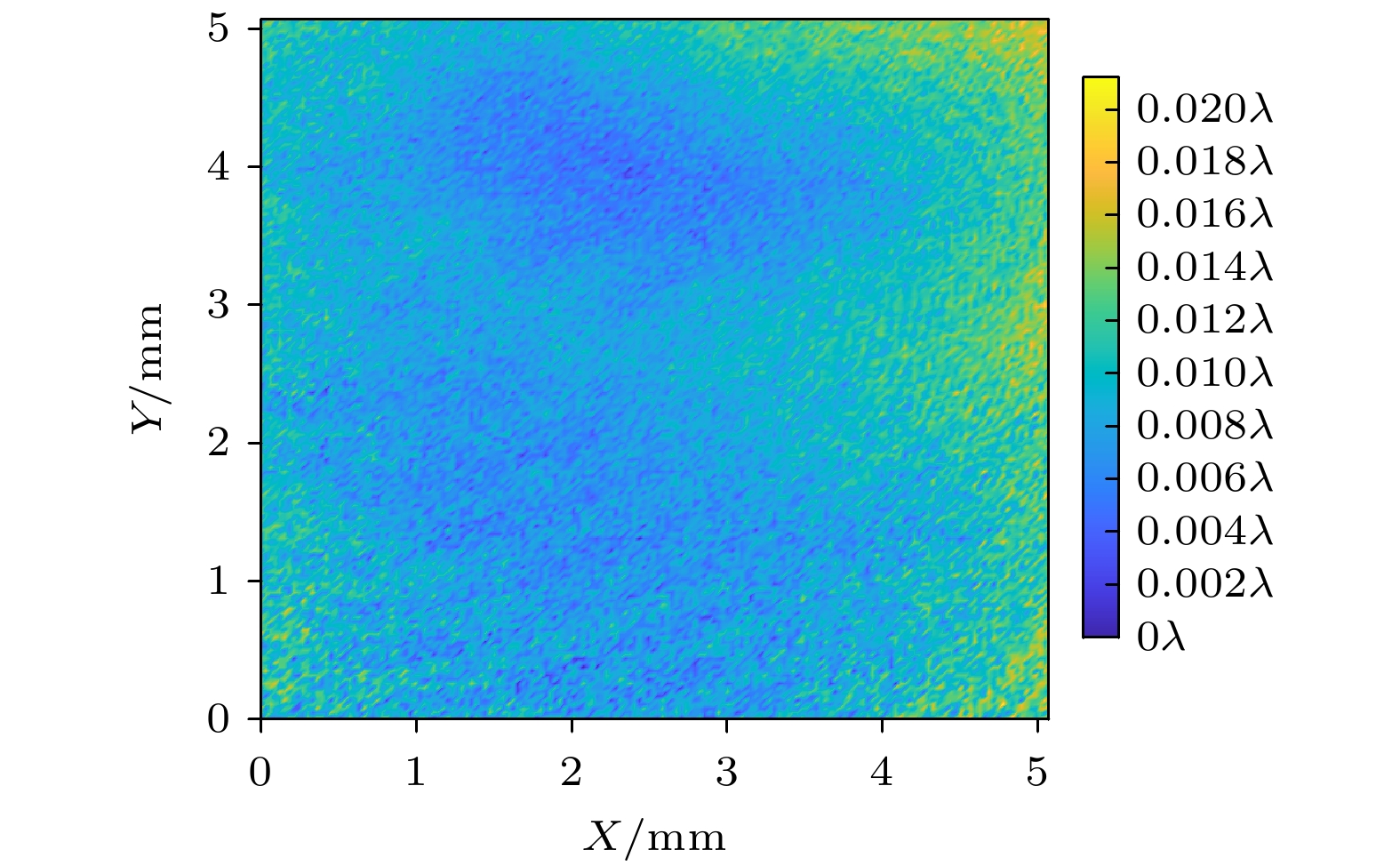
图 13 实验获得的干涉相位图及仿真图对比 (a)实验获得的干涉相位图; (b)根据实验结果拟合Zernike系数解算得到的相对位置信息获得的仿真干涉相位图
Figure 13. The experimental phase diagram compared with the simulation diagram: (a) Phase diagram obtained by experiment; (b) simulated phase diagram obtained from calculated relative position information based on experimental results fitting Zernike coefficients.
图 14 调节后的实验干涉相位图
Figure 14. Experimental interference phase diagram after displacement correction adjustment.
表 1 不同光纤相对姿态对应Zernike系数比较
Table 1. Comparison of Zernike coefficients corresponding to different kinds of alignment errors.
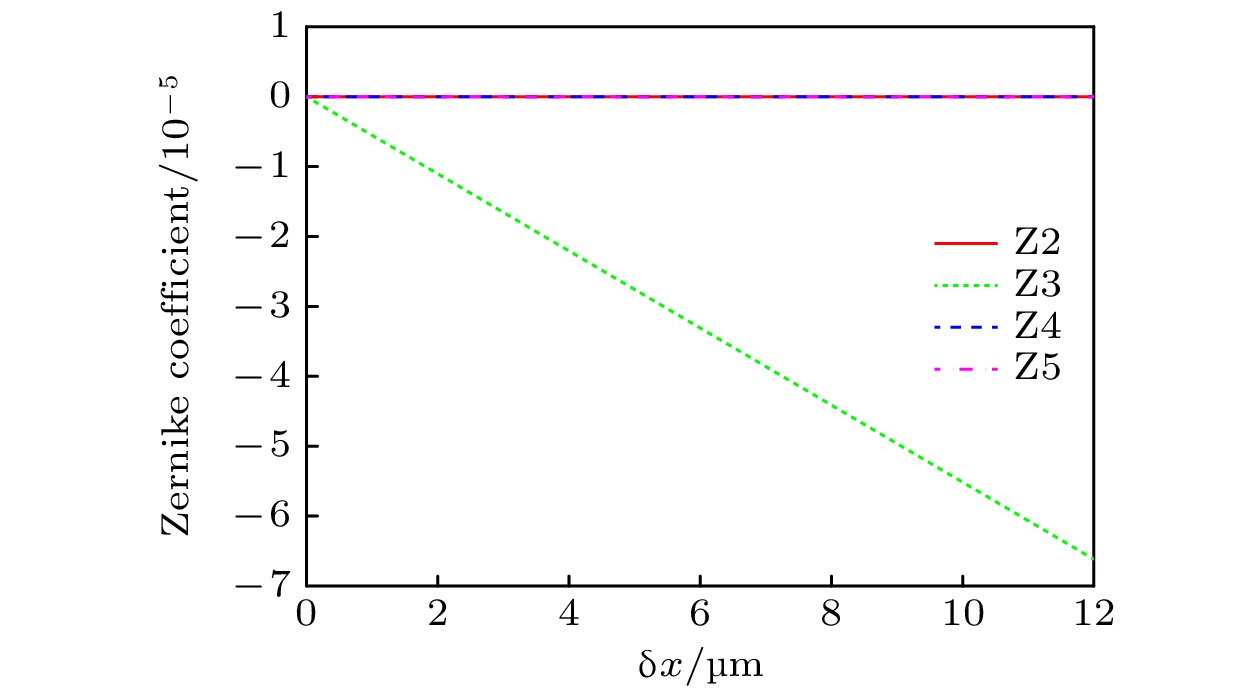
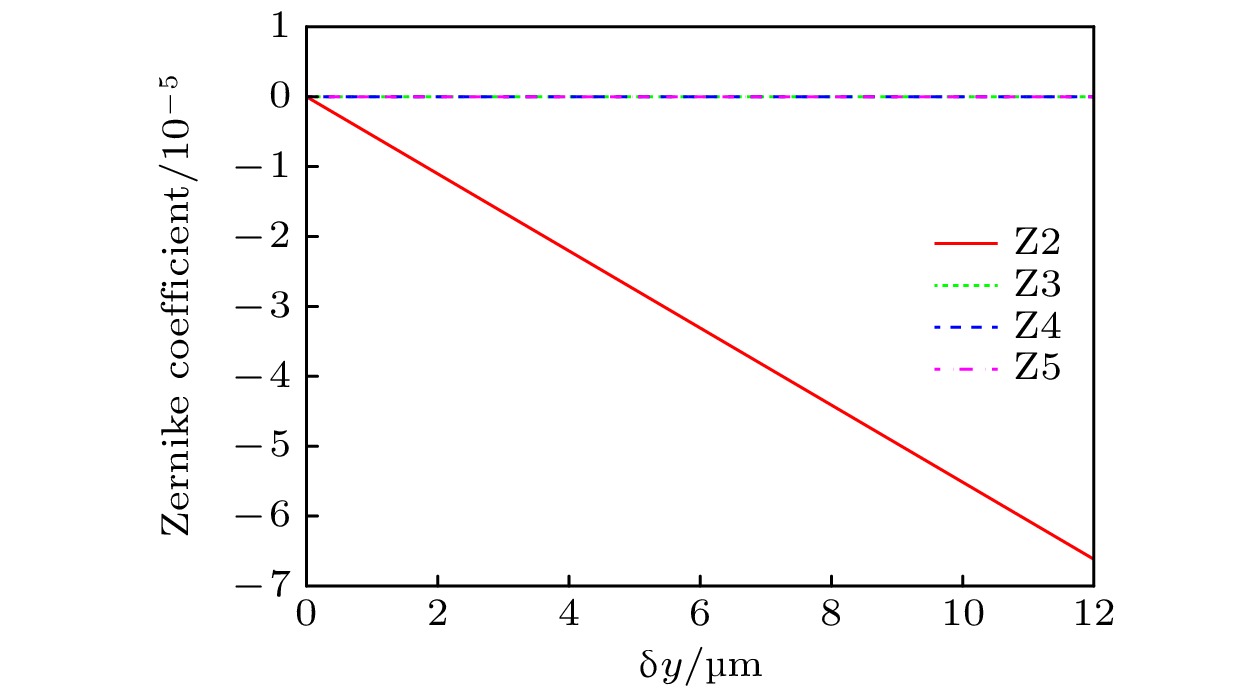
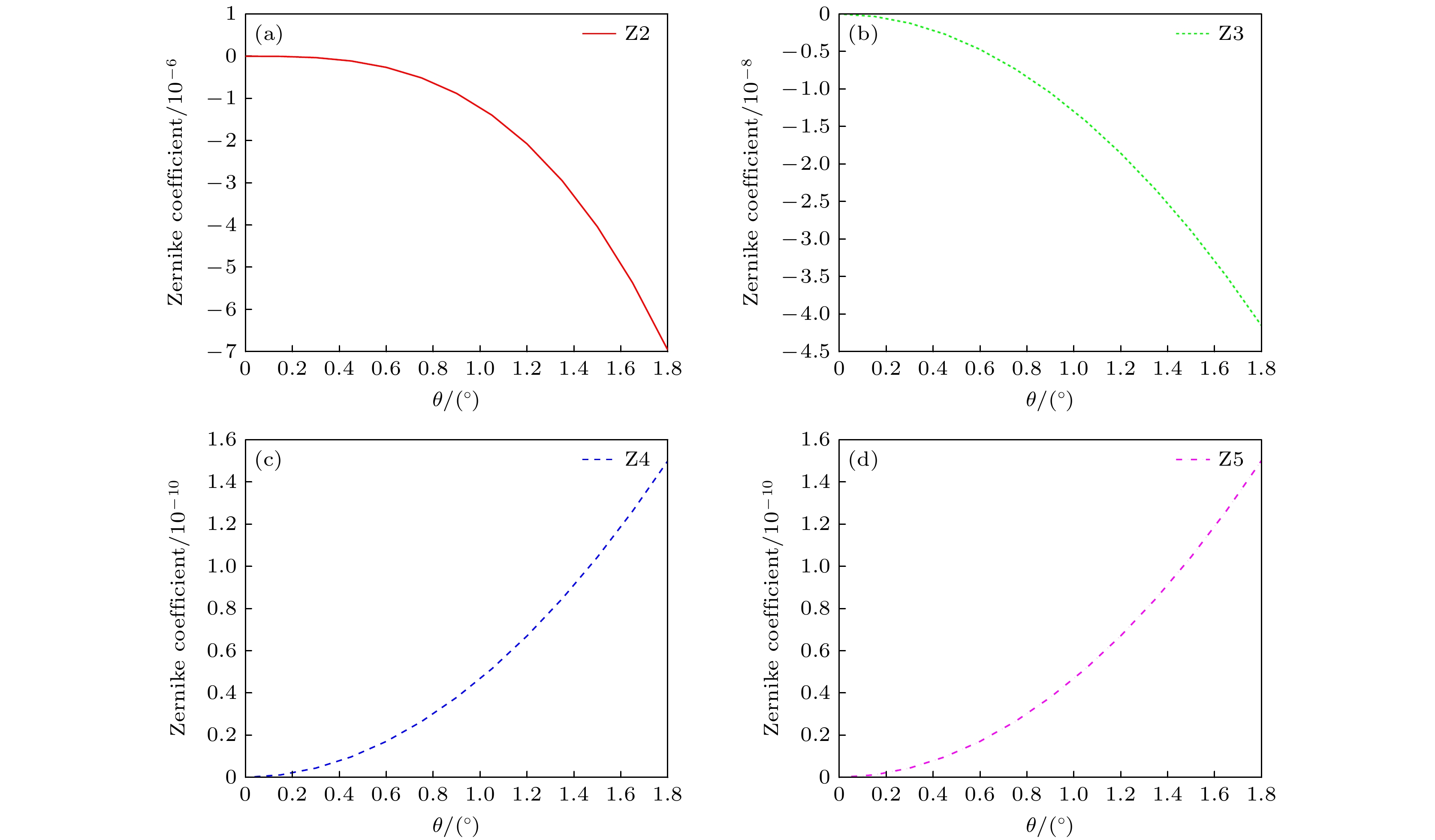
光纤相对姿态 Z2 Z3 Z4 Z5 δx/μm δy/μm δz/μm θ/(°) 2 3 5 0.5 –1.67×10–5 –1.10×10–5 2.14×10–11 1.20×10–11 2 0 0 0 –4.02×10–19 –1.10×10–5 1.85×10–22 1.08×10–21 0 3 0 0 –1.65×10–5 1.03×10–18 –1.41×10–21 8.87×10–22 0 0 5 0 –5.20×10–9 –5.20×10–9 9.38×10–12 –1.03×10–25 0 0 0 0.5 –1.54×10–7 –3.30×10–9 1.19×10–11 1.19×10–11 
DownLoad: CSV
表 2 不同光纤相对姿态对应耦合效率和波前PV值比较
Table 2. Comparison of coupling efficiency and wavefront PV value corresponding to different kinds of alignment errors.
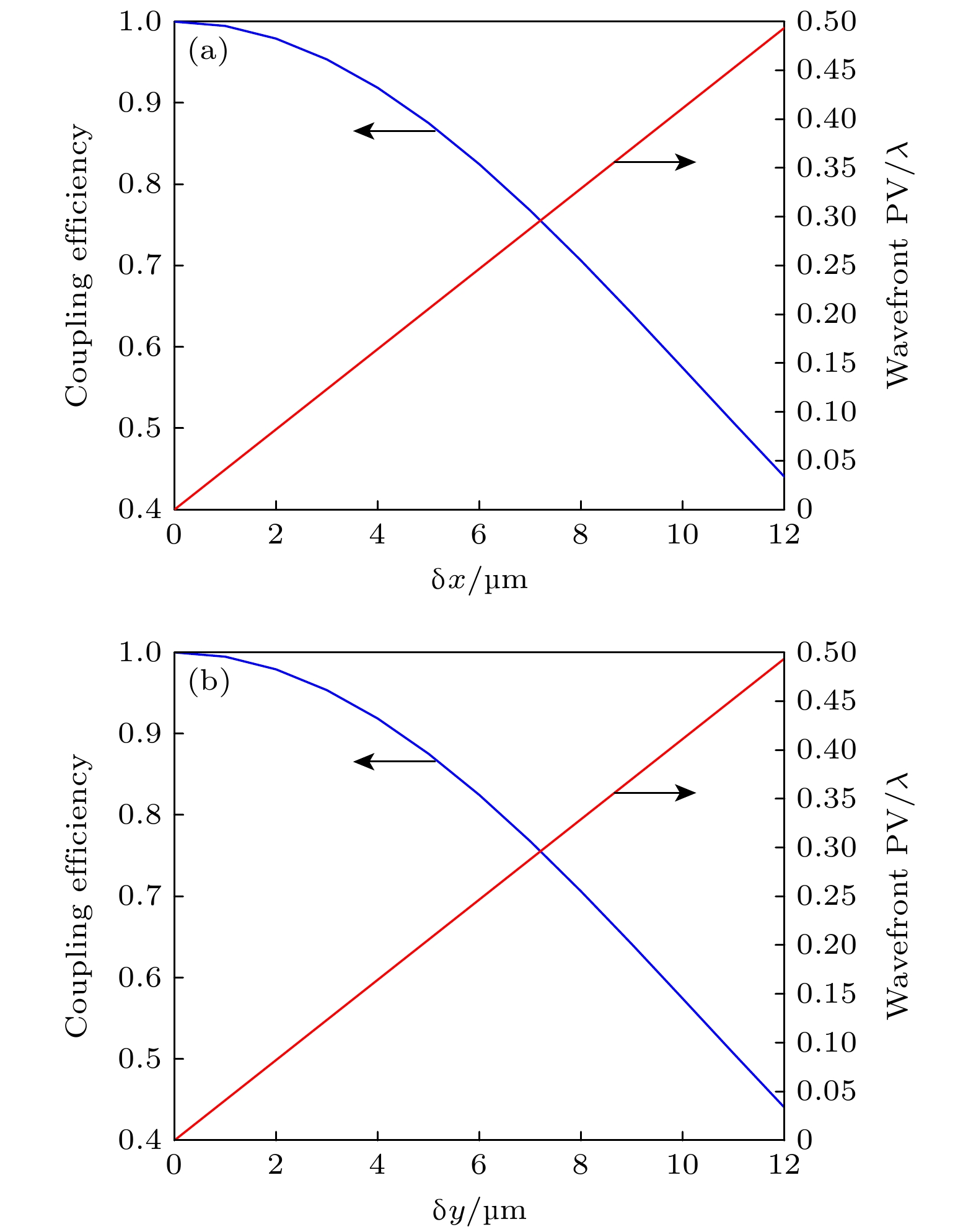
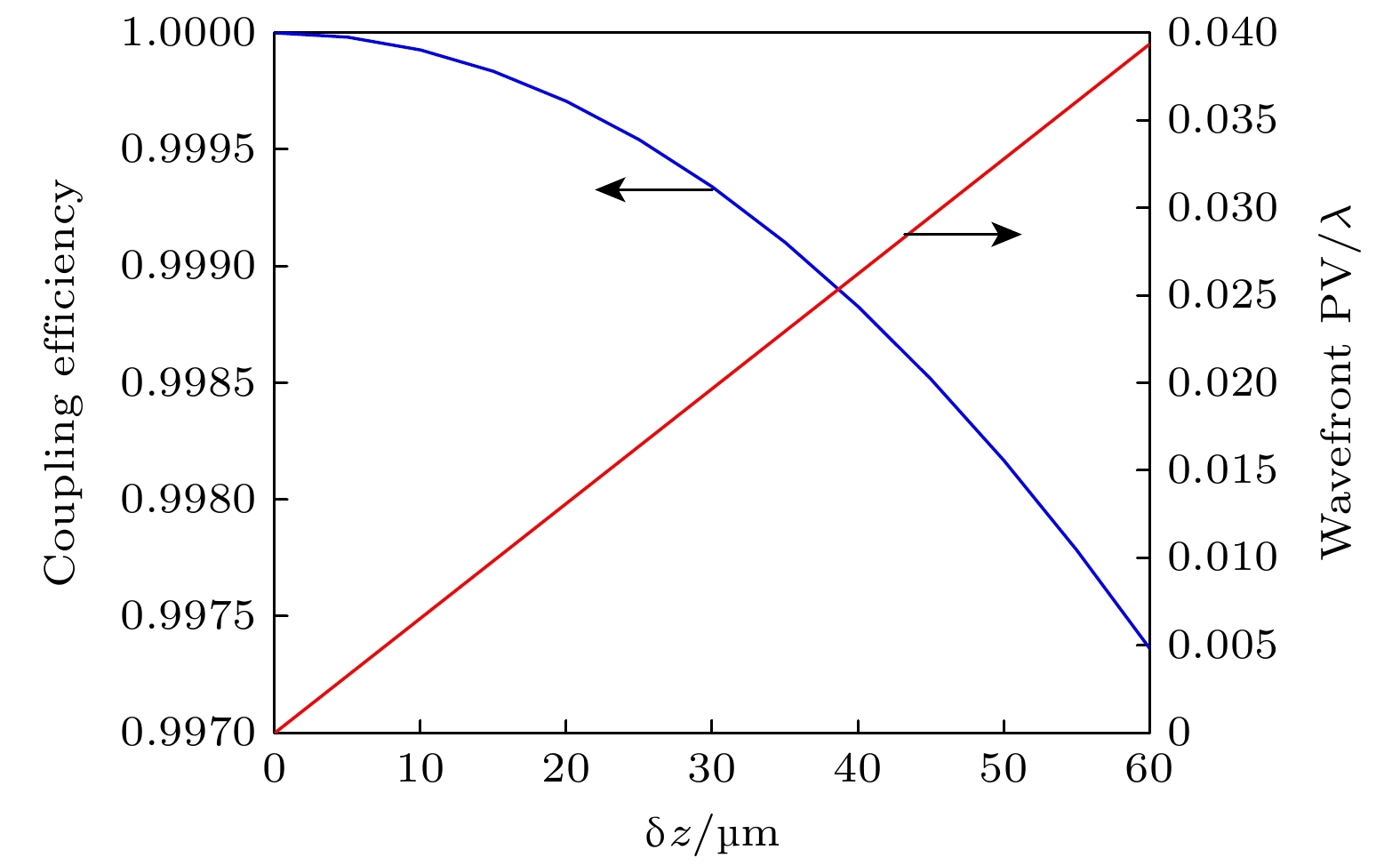
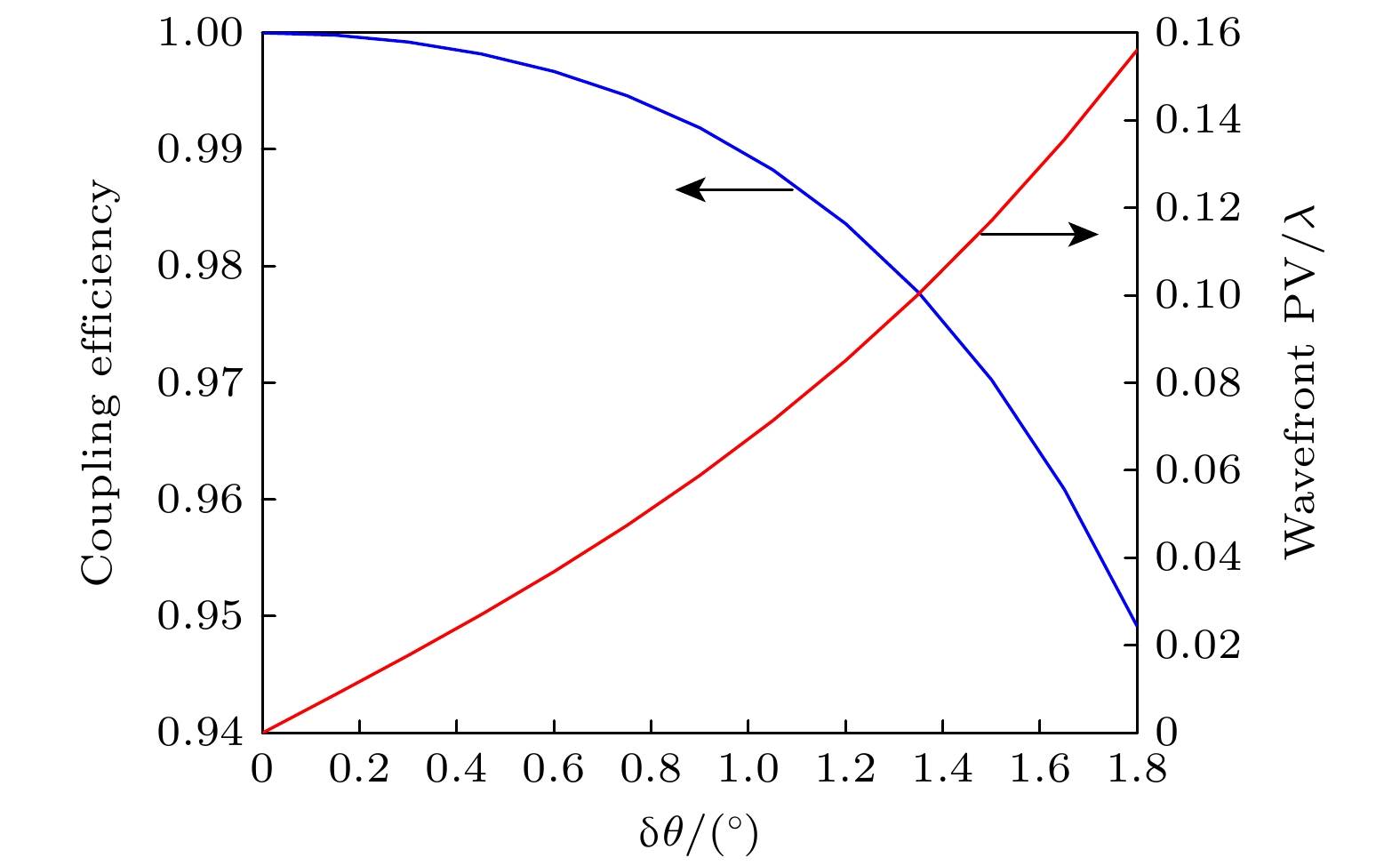
光纤相对姿态 耦合效率 波前PV/λ δx/μm δy/μm δz/μm θ/(°) 2 3 5 0.5 0.9215 0.2359 2 0 0 0 0.9792 0.0823 0 3 0 0 0.9536 0.1234 0 0 5 0 0.9999 0.0033 0 0 0 0.5 0.9978 0.0302
DownLoad: CSV
表 3 实验结果与对应Zernike系数比较
Table 3. Comparison of experimental results and simulation Zernike coefficients.
光纤相对姿态 Z2 Z3 Z4 Z5 δx/μm δy/μm δz/μm θ/(°) 实验值 — — — — 9.01×10–6 –2.74×10–6 2.28×10–11 –5.75×10–11 仿真值 0.5 –1.4 42 –1.1 9.31×10–6 –2.75×10–6 2.24×10–11 –5.65×10–11 0.5 0 0 0 2.26×10–19 –2.75×10–6 –2.28×10–22 –3.60×10–22 0 –1.4 0 0 7.71×10–6 –6.33×10–19 6.38×10–22 –1.01×10–21 0 0 42 0 –4.37×10–8 –4.37×10–8 7.88×10–11 1.30×10–24 0 0 0 –1.1 1.60×10–6 1.56×10–8 –5.64×10–11 –5.65×10–11
DownLoad: CSV
表 4 横向位移纠正后的实验结果与对应Zernike系数比较
Table 4. Comparison of experimental results after transverse displacement correction and simulation Zernike coefficients.
光纤相对姿态 Z2 Z3 Z4 Z5 δx/μm δy/μm δz/μm θ/(°) 实验值 — — — — –9.62×10–8 4.96×10–7 6.45×10–12 –1.79×10–11 仿真值 –0.09 0.02 — — –1.10×10–7 4.96×10–7 — — –0.09 0 0 0 –4.07×10–20 4.96×10–7 4.10×10–23 6.47×10–23 0 0.02 0 0 –1.10×10–7 9.04×10–21 –9.11×10–24 1.44×10–23
DownLoad: CSV
-
[1] 张琦, 王洪斌, 姜睿, 杜传宇 2022 航空发动机 48 76
Zhang Q, Wang H B, Jiang R, Du C Y 2022 Aeroengine 48 76
[2] Fu X, Liu Y Q, Hu X D, Li D C, Hu X T 2004 J. Optoelectron. Laser 11 1357
[3] Ebert R, Lutzmann P, Hebel M 2008 IEEE Photonics Global Singapore, 2008, p1
[4] Zhu Z, Li W, Molina E, Wolberg G 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 2007 p1
[5] 张文 2016 博士学位论文(杭州: 浙江大学)
Zhang W 2016 Ph. D. Dissertation (Hangzhou: Zhejiang University
[6] 刘爱东, 于梅 2015 振动与冲击 34 212
Liu A D, Yu M 2015 J. Vib. Shock 34 212
[7] 吕韬 2019 博士学位论文(长春: 中国科学院长春光学精密机械与物理研究所)
Lv T 2019 Ph. D. Dissertation (Changchun: Chinese Academy of Sciences Changchun Institute of Optics Fine Mechanics and Physics
[8] Li R, Poulos N M, Zhu Z G, Xie L P 2012 Appl. Opt. 51 5011
Google Scholar
[9] Han X Y, Lv T, Wu S S, Li Y Y, He B 2019 Opt. Laser Technol. 111 575
Google Scholar
[10] He Q, Zhao Z G, Ye X D, Luo C, Zhang D C, Wang S F, Xu X P 2022 Micromachines 13 324
Google Scholar
[11] Alaruri S D 2015 Optik 126 5923
Google Scholar
[12] Liu X Y, Guo J, Li G N, Chen N, Shi K 2019 Results Phys. 12 1044
Google Scholar
[13] Zhang M Q, Zhi D, Chang Q, Ma P F, Ma Y X, Su R T, Wu J, Zhou P, Si L 2019 Laser Phys. 29 115101
Google Scholar
[14] Yan Y X, Zheng Y, Duan J A, Huang Z L 2020 Opt. Fiber Technol. 58 102301
Google Scholar
[15] Phattaraworamet T, Saktioto T, Ali J, Fadhali M, Yupapin P P, Zainal J, Mitatha S 2010 Optik 121 2240
Google Scholar
[16] 丁莉, 刘代中, 高妍琦, 朱宝强, 朱俭, 彭增云, 朱健强, 俞立钧 2008 57 5713
Google Scholar
Ding L, Liu D Z, Gao Y Q, Zhu B Q, Zhu J, Peng Z Y, Zhu J Q, Yu L J 2008 Acta Phys. Sin. 57 5713
Google Scholar
[17] 陶嘉庆, 胡越, 项华中, 涂建坤, 郑刚 2021 电子科技 34 37
Google Scholar
Tao J Q, Hu Y, Xiang Z H, Tu J K, Zheng G 2021 Electron. Sci. Technol. 34 37
Google Scholar
[18] Zhu M X, Bai F Z, Gan S M, Huang K Z, Huang L H, Wang J X 2013 Optik 124 5624
Google Scholar
[19] Wallner O, Winzer P J, Leeb W R 2002 Appl. Opt. 41 637
Google Scholar
[20] Kang J M, Guo P, Zhang Y C, Chen H, Chen S Y, Ge X Y 2013 SPIE Fifth International Symposium on Photoelectronic Detection and Imaging Beijing, China, June 25, 2013 p891417
DownLoad:
Catalog
Metrics
- Abstract views: 1913
- PDF Downloads: 46
- Cited By: 0
