-
The formation and evolution of hotspots is important for achieving ignition and high energy gain in inertial fusion process. However, most of relevant studies are carried out on pre-compressed plasmas with an isobaric configuration, the evolution of the hotspot in a plasma with an isochoric configuration is rarely studied. In this paper, a semi-analytical model is developed to describe the evolution of the hotspot boundary and propagation of fusion burning waves for a high-density pre-compressed plasma with an isochoric configuration in the double-cone ignition scheme. For the shock wave, the strong shock wave approximation and the quasi-isobaric approximation are reasonable. The quasi-isobaric approximation shows that as the plasma density behind the shock wave increases, the plasma temperature decreases. Because of these, the range of
$ {\mathrm{\alpha }} $ -particles decreases rapidly behind the shock wave, forming an$ {\mathrm{\alpha }} $ -particle absorption peak. Therefore, considering that the hotspot is the main region where$ {\mathrm{\alpha }} $ -particles are produced and deposited, the position of the shock peak can be used to identify the boundary of the hotspot in a high-density plasma with an isochoric configuration. It also shows that a “self-regulating burning process” exists in the burning process of the isochoric hotspot, most of$ {\mathrm{\alpha }} $ -particles are deposited in the stable region and behind the shock, and finally, transport through the shock peak and heat the cold fuel, resulting in the temperature rising. In the high-density hotspots of plasma with an isochoric configuration, the deposition of α-particles behaves as an obvious non-uniform distribution effect. By analyzing the non-uniform deposition of α-particles, the deposition rate of α-particles at the edge of spherical uniform hotspot is calculated, then the temperature and density evolution of the isochoric hotspot can be well described. The model can be used to estimate the Lawson parameter of the hotspots at the end of the early stage of ignition. It is found that a lower fast electron energy is more beneficial to ignition and high gain operation of fusion plasma. It is also shown that the high density of the hotspots in the isochoric plasma will lead to a higher fusion burning rate, which can offset the negative influence of the shock wave and even achieve higher energy gain. The semi-analytical model is verified by the hydrodynamic simulations of O-SUKI-N.-
Keywords:
- pre-compressed isochoric plasma /
- fast ignition /
- hotspot evolution /
- $ {\mathrm{\alpha }} $-particles deposition
[1] Nuckolls J, Wood L, Thiessen A, Zimmerman G 1972 Nature 239 139
Google Scholar
[2] Tabak M, Hammer J, Glinsky M E, Kruer W L, Wilks S C, Woodworth J, Campbell E M, Perry M D, Mason R J 1994 Phys. Plasmas 1 1626
Google Scholar
[3] Zhang J, Wang W M, Yang X H, Wu D, Ma Y Y, Jiao J L, Zhang Z, Wu F Y, Yuan X H, Li Y T, Zhu J Q 2020 Philos. Trans. R. Soc. London, Ser. A 378 20200015
[4] Lan K 2022 Matter Radiat. Extrem. 7 055701
Google Scholar
[5] Tollefson J, Gibney E 2022 Nature 612 597
Google Scholar
[6] Lawson J D 1957 Proc. Trans. R. Soc. London, Ser. B 70 6
Google Scholar
[7] Atzeni S, Meyer-ter-Vehn J 2004 The Physics of Inertial Fusion (New York : Oxford University Press) pp44, 48
[8] Olson R E, Leeper R J, Yi S A, et al. 2016 J. Phys. Conf. Ser. 717 012042
Google Scholar
[9] Patel P K, Springer P T, Weber C R, et al. 2020 Phys. Plasmas 27 050901
Google Scholar
[10] 杨孟奇, 吴福源, 陈致博, 张翼翔, 陈一, 张晋川, 陈致真, 方志凡, Rafael Ramis, 张杰 2022 71 225202
Google Scholar
Yang M Q, Wu F Y, Chen Z B, Zhang Y X, Chen Y, Zhang J C, Chen Z Z, Fang Z F, Rafael R, Zhang J 2022 Acta Phys. Sin. 71 225202
Google Scholar
[11] 张喆, 远晓辉, 张翌航, 刘浩, 方可, 张成龙, 刘正东, 赵旭, 董全力, 刘高扬, 戴羽, 谷昊琛, 李玉同, 郑坚, 仲佳勇, 张杰 2022 71 155201
Google Scholar
Zhang Z, Yuan X H, Zhang Y H, Liu H, Fang K, Zhang C L, Liu Z D, Zhao X, Dong Q L, Liu G Y, Dai Y, Gu H C, Li Y T, Zheng J, Zhong J Y, Zhang J 2022 Acta Phys. Sin. 71 155201
Google Scholar
[12] Wu F, Yang X, Ma Y, et al. 2022 High Power Laser Sci. Eng. 10 e12
Google Scholar
[13] Song H, Wu F, Sheng Z, Zhang J 2023 Phys. Plasmas 30 092707
Google Scholar
[14] Xu Z, Wu F, Jiang B, Kawata S, Zhang J 2023 Nucl. Fusion 63 126062
Google Scholar
[15] Nakamura H, Uchibori K, Kawata S, Karino T, Sato R, Ogoyski A I 2022 Comput. Phys. Commun. 272 108223
Google Scholar
[16] Ramis R, Meyer-ter-Vehn J, Ramírez J 2009 Comput. Phys. Commun. 180 977
Google Scholar
[17] Wu F, Chu Y, Ramis R, et al. 2018 Matter Radiat. Extrem. 3 248
Google Scholar
[18] Krokhin O N, Rozanov V B 1973 Sov. J. Quantum Electron. 2 393
Google Scholar
[19] Fraley G S 1974 Phys. Fluids 17 474
Google Scholar
[20] Frenje J A, Grabowski P E, Li C K, et al. 2015 Phys. Rev. Lett. 115 205001
Google Scholar
[21] Spitzer L 2006 Physics of Fully Ionized Gases (2nd rev. ed.) (Mineola, NY: Dover Publications) p170
[22] Zylstra A B, Hurricane O A 2019 Phys. Plasmas 26 062701
Google Scholar
[23] Solodov A A, Betti R 2008 Phys. Plasmas 15 042707
Google Scholar
[24] Betti R, Hurricane O A 2016 Nat. Phys. 12 435
Google Scholar
[25] Zylstra A B, Hurricane O A, Callahan D A, et al. 2022 Nature 601 542
Google Scholar
-
图 1 双锥对撞点火方案中等容预压缩等离子体密度分布
Figure 1. Density distribution of isochoric pre-compressed plasma in double-cone ignition scheme.
图 2 (a) 等容预拼装等离子体密度温度示意图; (b) O-SUKI-N程序给出的等容预拼装等离子体在燃烧过程中的温度、密度和压强分布, 靶丸被划分为中心燃烧区域、激波区域和冷燃料区域. 此时初始热斑温度为$ 9\;{\mathrm{k}}{\mathrm{e}}{\mathrm{V}} $, 图中所取基准值${T}_{0}=5\;{\mathrm{k}}{\mathrm{e}}{\mathrm{V}}, $ $ {\rho }_{0}=100\;{\mathrm{g}}/{\mathrm{c}}{\mathrm{c}} $, ${P}_{0}={10}^{3}\;{\mathrm{G}}{\mathrm{b}}{\mathrm{a}}{\mathrm{r}} $
Figure 2. (a) Density and temperature of isochoric pre-assembled plasma. (b) The temperature, density, and pressure distribution of the isochoric pre-assembly plasma in the burning process given by O-SUKI-N. The target is divided into central burning zone, shock wave, and cold fuel by density. The initial hotspot temperature is $ 9\;{\mathrm{k}}{\mathrm{e}}{\mathrm{V}} $, and the reference value is $ {T}_{0}=5\;{\mathrm{k}}{\mathrm{e}}{\mathrm{V}}, ~ {\rho }_{0}= $$ 100\;{\mathrm{g}}/{\mathrm{c}}{\mathrm{c}}, {P}_{0}={10}^{3}\;{\mathrm{G}}{\mathrm{b}}{\mathrm{a}}{\mathrm{r}} $.
图 3 O-SUKI-N程序给出的燃烧过程中等离子体参数和$ {\mathrm{\alpha }} $粒子吸收峰, 此时初始热斑温度为$ 9\;{\mathrm{k}}{\mathrm{e}}{\mathrm{V}} $ (a) 密度曲线(蓝色)与$ {\mathrm{\alpha }} $粒子沉积$ {n}_{{\mathrm{\alpha }}}{\omega }_{{\mathrm{\alpha }}} $分布曲线(红色); (b) 等离子体温度T、密度$\rho $和$ {\mathrm{\alpha }} $粒子沉积$ {n}_{{\mathrm{\alpha }}}{\omega }_{{\mathrm{\alpha }}} $分布
Figure 3. The plasma parameters and α-particle absorption peak during burning process given by O-SUKI-N, and the initial hotspot temperature is $ 9\;{\mathrm{k}}{\mathrm{e}}{\mathrm{V}} $: (a) Density distribution (blue), α-particle deposition $ {n}_{{\mathrm{\alpha }}}{\omega }_{{\mathrm{\alpha }}} $ distribution (red); (b) temperature T, density of plasma $\rho $ and $ {\mathrm{\alpha }} $-particle deposition $ {n}_{{\mathrm{\alpha }}}{\omega }_{{\mathrm{\alpha }}} $.
图 4 $ {\mathrm{\alpha }} $粒子空间非均匀沉积模型示意图
Figure 4. Schematic diagram of the non-uniform deposition model of $ {\mathrm{\alpha }} $-particle.
图 5 初始热斑温度为$ 9\;{\mathrm{ }}{\mathrm{k}}{\mathrm{e}}{\mathrm{V}} $条件下, O-SUKI-N程序给出的燃烧过程中$ -\dfrac{1}{T}\dfrac{\partial T}{\partial r} $(蓝色实线), $ \dfrac{1}{\rho }\dfrac{\partial \rho }{\partial r} $(蓝色虚线)和$ {\mathrm{\alpha }} $粒子沉积分布$ {n}_{{\mathrm{\alpha }}}{\omega }_{{\mathrm{\alpha }}} $(红色实线)分布, 图中黑色虚线对应激波波峰的位置, $ {{\overline T}_{h}} $是热斑平均温度 (a)$ {{\overline T}_{h}}=10.99\;{\mathrm{keV}} $; (b) $ {{\overline T}_{h}}=14.46\;{\mathrm{keV}} $; (c) $ {{\overline T}_{h}}=22.65\;{\mathrm{keV}} $
Figure 5. Distribution of $ -\dfrac{1}{T}\dfrac{\partial T}{\partial r} $ (blue solid line), $ \dfrac{1}{\rho }\dfrac{\partial \rho }{\partial r} $ (blue dashed line) and α-particle deposition $ {n}_{{\mathrm{\alpha }}}{\omega }_{{\mathrm{\alpha }}} $ (red solid line) in the burning process when the initial hotspot temperature is $ 9\;{\mathrm{ }}{\mathrm{k}}{\mathrm{e}}{\mathrm{V}} $ given by O-SUKI-N. The black dashed line corresponds to the position of the shock peak, and $ {{\overline T}_{{\mathrm{h}}}} $ is the average temperature of the hotspot (a) ${{\overline T}_{h}}=10.99\;{\mathrm{keV}} $; (b) $ {{\overline T}_{h}}=14.46\;{\mathrm{keV}} $; (c) ${{\overline T}_{h}}=22.65\;{\mathrm{keV}} $.
图 6 半解析模型、Krokhin模型与O-SUKI-N程序计算结果对比, 图中黑色虚线标明了点火初期结束时刻
Figure 6. Comparison of results of semi-analytic model, Krokhin model, and O-SUKI-N under different conditions. The black dashed line indicates the end of the early stage of ignition.
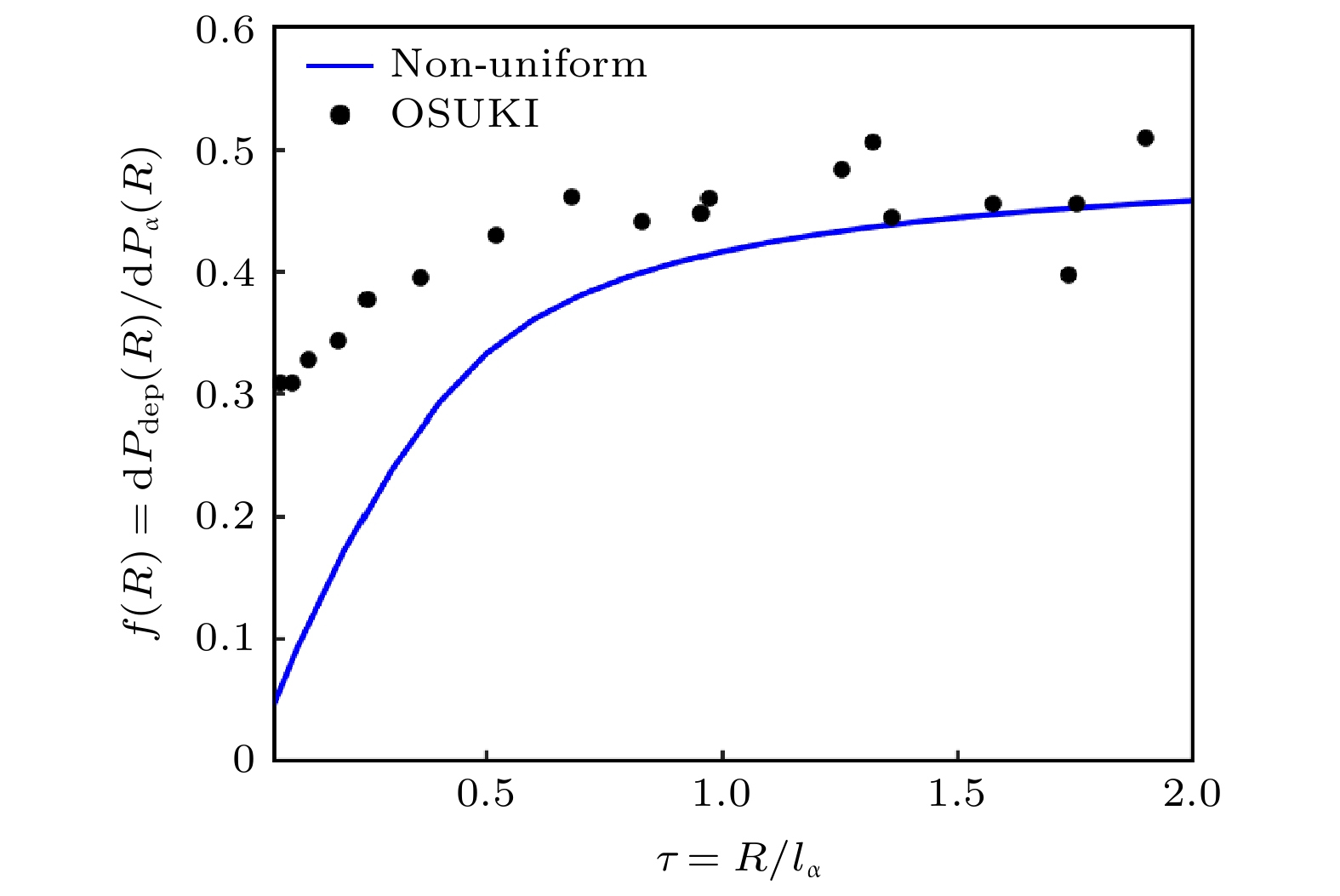
图 7 不均匀沉积模型与O-SUKI-N程序稳定区域边缘不均匀沉积函数$ {f}_{{\mathrm{n}}{\mathrm{o}}{\mathrm{n}}}\left(R\right) $和$ {f}_{{\mathrm{O}}{\mathrm{S}}{\mathrm{U}}}\left(R\right) $对比
Figure 7. Comparison of non-uniform deposition function $ {f}_{{\mathrm{n}}{\mathrm{o}}{\mathrm{n}}}\left(R\right) $ and $ {f}_{{\mathrm{O}}{\mathrm{S}}{\mathrm{U}}}\left(R\right) $ at the stable zone edge of the non-uniform deposition mode model with O-SUKI-N.
图 8 快电子总能量$ 3\;{\mathrm{ }}{\mathrm{k}}{\mathrm{J}} $条件下半解析模型与数值模拟程序O-SUKI-N对比 (a) 点火初期结束时刻的热斑劳森参数$ P\tau $(蓝色)和热斑平均温度$ \overline{T} $(红色)对比; (b) $ {\mathrm{\alpha }} $粒子加热倍率$ {Q}_{{\mathrm{\alpha }}} $
Figure 8. Comparison between the semi-analytical model and the simulation program O-SUKI-N when the total fast electron energy is 3 kJ: (a) Comparison of the Lawson parameter $ P\tau $ (blue) and average temperature $ \overline{T} $ (red) of the hotspot at the end of the early stage of ignition; (b) comparison of $ {Q}_{\alpha } $.
表 1 均匀球形热斑中$ {\mathrm{\alpha }} $粒子的产生与沉积区域
Table 1. Production and deposition of $ {\mathrm{\alpha }} $-particles in uniform spherical hotspots.
$ {\mathrm{\alpha }} $粒子产生区域 $ {\mathrm{\alpha }} $粒子沉积区域 符号 中心球体 ($ 0\leqslant r < R-{\mathrm{d}}R $) 中心球体 ($ 0\leqslant r < R-{\mathrm{d}}R $) $ {E}_{{\mathrm{d}}{\mathrm{e}}{\mathrm{p}}}(R-{\mathrm{d}}R\to R-{\mathrm{d}}R) $ 中心球体 $ (0\leqslant r < R-{\mathrm{d}}R $) 球壳 ($ R-{\mathrm{d}}R\leqslant r\leqslant R $) $ {E}_{{\mathrm{d}}{\mathrm{e}}{\mathrm{p}}}(R-{\mathrm{d}}R\to {\mathrm{d}}R) $ 球壳$ (R-{\mathrm{d}}R\leqslant r\leqslant R) $ 中心球体 ($ 0\leqslant r < R-{\mathrm{d}}R $) $ {E}_{{\mathrm{d}}{\mathrm{e}}{\mathrm{p}}}({\mathrm{d}}R\to R-{\mathrm{d}}R) $ 球壳 ($ R-{\mathrm{d}}R\leqslant r\leqslant R $) 球壳 ($ R-{\mathrm{d}}R\leqslant r\leqslant R $) $ {E}_{{\mathrm{d}}{\mathrm{e}}{\mathrm{p}}}({\mathrm{d}}R\to {\mathrm{d}}R) $ 
DownLoad: CSV
-
[1] Nuckolls J, Wood L, Thiessen A, Zimmerman G 1972 Nature 239 139
Google Scholar
[2] Tabak M, Hammer J, Glinsky M E, Kruer W L, Wilks S C, Woodworth J, Campbell E M, Perry M D, Mason R J 1994 Phys. Plasmas 1 1626
Google Scholar
[3] Zhang J, Wang W M, Yang X H, Wu D, Ma Y Y, Jiao J L, Zhang Z, Wu F Y, Yuan X H, Li Y T, Zhu J Q 2020 Philos. Trans. R. Soc. London, Ser. A 378 20200015
[4] Lan K 2022 Matter Radiat. Extrem. 7 055701
Google Scholar
[5] Tollefson J, Gibney E 2022 Nature 612 597
Google Scholar
[6] Lawson J D 1957 Proc. Trans. R. Soc. London, Ser. B 70 6
Google Scholar
[7] Atzeni S, Meyer-ter-Vehn J 2004 The Physics of Inertial Fusion (New York : Oxford University Press) pp44, 48
[8] Olson R E, Leeper R J, Yi S A, et al. 2016 J. Phys. Conf. Ser. 717 012042
Google Scholar
[9] Patel P K, Springer P T, Weber C R, et al. 2020 Phys. Plasmas 27 050901
Google Scholar
[10] 杨孟奇, 吴福源, 陈致博, 张翼翔, 陈一, 张晋川, 陈致真, 方志凡, Rafael Ramis, 张杰 2022 71 225202
Google Scholar
Yang M Q, Wu F Y, Chen Z B, Zhang Y X, Chen Y, Zhang J C, Chen Z Z, Fang Z F, Rafael R, Zhang J 2022 Acta Phys. Sin. 71 225202
Google Scholar
[11] 张喆, 远晓辉, 张翌航, 刘浩, 方可, 张成龙, 刘正东, 赵旭, 董全力, 刘高扬, 戴羽, 谷昊琛, 李玉同, 郑坚, 仲佳勇, 张杰 2022 71 155201
Google Scholar
Zhang Z, Yuan X H, Zhang Y H, Liu H, Fang K, Zhang C L, Liu Z D, Zhao X, Dong Q L, Liu G Y, Dai Y, Gu H C, Li Y T, Zheng J, Zhong J Y, Zhang J 2022 Acta Phys. Sin. 71 155201
Google Scholar
[12] Wu F, Yang X, Ma Y, et al. 2022 High Power Laser Sci. Eng. 10 e12
Google Scholar
[13] Song H, Wu F, Sheng Z, Zhang J 2023 Phys. Plasmas 30 092707
Google Scholar
[14] Xu Z, Wu F, Jiang B, Kawata S, Zhang J 2023 Nucl. Fusion 63 126062
Google Scholar
[15] Nakamura H, Uchibori K, Kawata S, Karino T, Sato R, Ogoyski A I 2022 Comput. Phys. Commun. 272 108223
Google Scholar
[16] Ramis R, Meyer-ter-Vehn J, Ramírez J 2009 Comput. Phys. Commun. 180 977
Google Scholar
[17] Wu F, Chu Y, Ramis R, et al. 2018 Matter Radiat. Extrem. 3 248
Google Scholar
[18] Krokhin O N, Rozanov V B 1973 Sov. J. Quantum Electron. 2 393
Google Scholar
[19] Fraley G S 1974 Phys. Fluids 17 474
Google Scholar
[20] Frenje J A, Grabowski P E, Li C K, et al. 2015 Phys. Rev. Lett. 115 205001
Google Scholar
[21] Spitzer L 2006 Physics of Fully Ionized Gases (2nd rev. ed.) (Mineola, NY: Dover Publications) p170
[22] Zylstra A B, Hurricane O A 2019 Phys. Plasmas 26 062701
Google Scholar
[23] Solodov A A, Betti R 2008 Phys. Plasmas 15 042707
Google Scholar
[24] Betti R, Hurricane O A 2016 Nat. Phys. 12 435
Google Scholar
[25] Zylstra A B, Hurricane O A, Callahan D A, et al. 2022 Nature 601 542
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 2205
- PDF Downloads: 120
- Cited By: 0
