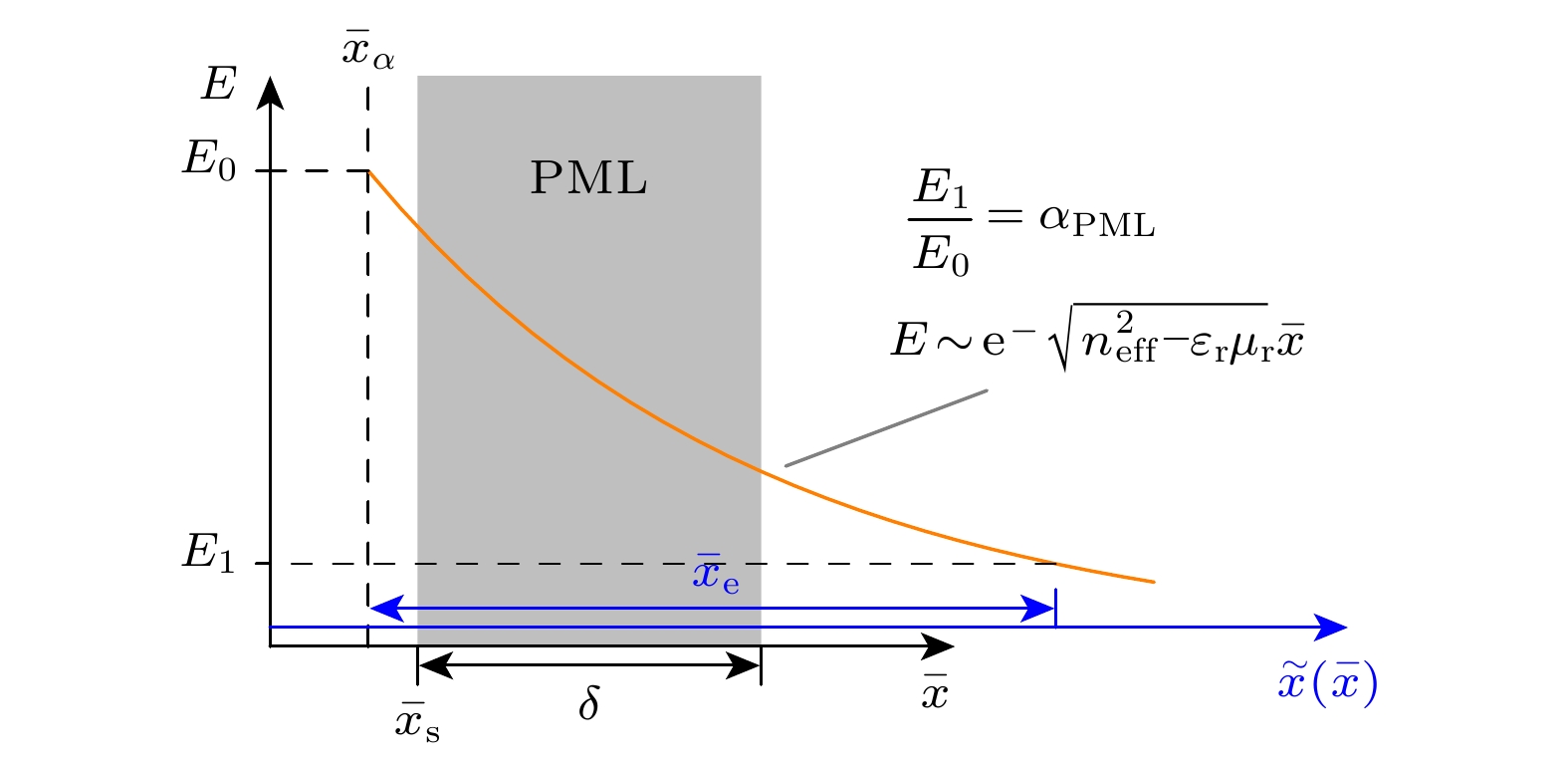
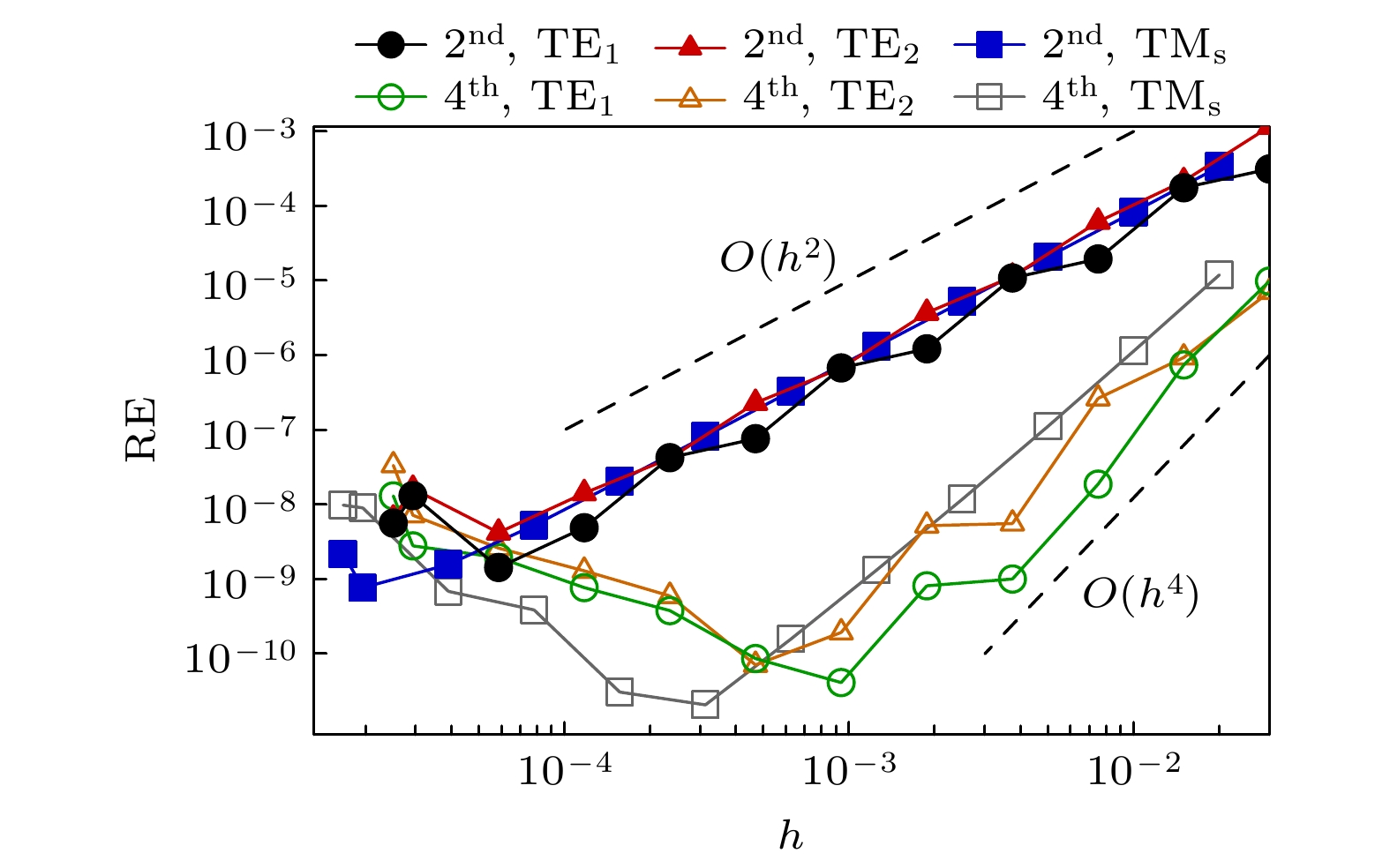
-
Modal analysis of optical waveguides is a basic task in the design of advanced waveguide devices and optical circuits. How to deal with the problem of electromagnetic heterogeneous interface and absorption boundary condition are two major difficulties in implementing efficient numerical analysis of optical waveguides. Existing high-order accurate finite-difference modal analysis methods do not take into consideration the absorption boundary problem, which, thus, makes it difficult to accurately simulate leakage and radiation modes. Based on the immersed interface method and perfectly matched layer absorption boundary condition, a finite-difference method with the second- and fourth-order accuracy is proposed in this work. By using this method, the single-interface plasmonic waveguide mode, planar symmetric waveguide mode, and one-dimensional photonic crystal waveguide mode are analyzed. Numerico-experimental results show that the convergence rate of the second- and fourth-order algorithm are consistent with the anticipated order of the guided mode, leakage mode and radiation mode. The second-order algorithm provides an ultimate accuracy of about
$10^{-9}$ for the relative error of effective refractive index, when the normalized step size is$10^{-4}$ . The fourth-order algorithm provides an ultimate accuracy of about$10^{-10}$ for the relative error of effective refractive index, when the normalized step size is$10^{-3}$ . Through the study of field distribution of guided mode and cladding mode in a one-dimensional photonic crystal waveguide, we show that the continuity of the field of transverse electric mode and its first derivative across the interface, and the continuity of the field of transverse magnetic mode and the discontinuity of its first derivative across interface, can be analyzed accurately. The method proposed in this paper can be used to calculate any mode for any refractive index profile, only by using the value of refractive index, independent of the specific functional representation of modal fields. The method provides a simple and efficient tool for implementing the modal analysis of step-index planar waveguides.-
Keywords:
- immersed interface method /
- perfectly matched layer /
- waveguide mode
[1] 陈宪锋, 沈小明, 蒋美萍, 金铱 2008 57 3578
Google Scholar
Chen X F, Shen X M, Jiang M P, Jin Y 2008 Acta Phys. Sin. 57 3578
Google Scholar
[2] 陈云天, 王经纬, 陈伟锦, 徐竞 2020 69 154206
Google Scholar
Chen Y T, Wang J W, Chen W J, Xu J 2020 Acta Phys. Sin. 69 154206
Google Scholar
[3] 李慧慧, 薛文瑞, 李宁, 杜易达, 李昌勇 2022 71 108101
Google Scholar
Li H H, Xue W R, Li N, Du Y D, Li C Y 2022 Acta Phys. Sin. 71 108101
Google Scholar
[4] 乔海亮, 王玥, 陈再高, 张殿辉 2013 62 070204
Google Scholar
Qiao H L, Wang Y, Chen Z G, Zhang D H 2013 Acta Phys. Sin. 62 070204
Google Scholar
[5] Wu D, Ohnishi R, Uemura R, Yamaguchi R, Ohnuki S 2018 IEEE Photonics Technol. Lett. 30 1024
Google Scholar
[6] LeVeque R J, Li Z L 1994 SIAM J. Numer. Anal. 31 1019
Google Scholar
[7] LeVeque R J, Li Z L 1995 SIAM J. Numer. Anal. 32 1704
Google Scholar
[8] Horikis T P, Kath W L 2006 Opt. Lett. 31 3417
Google Scholar
[9] Horikis T P 2011 Int. J. Mod. Phys. C 22 687
Google Scholar
[10] Horikis T P 2013 Appl. Math. Model. 37 5080
Google Scholar
[11] Stern M S 1988 IEE Proc. J. (Optoelectron.) 135 56
Google Scholar
[12] Vassallo C 1992 IEE Proc. J. (Optoelectron.) 139 137
Google Scholar
[13] Yamauchi J, Sekiguchi M, Uchiyama O, Shibayama J, Nakano H 1997 IEEE Photonics Technol. Lett. 9 961
Google Scholar
[14] Yamauchi J, Takahashi G, Nakano H 1998 IEEE Photonics Technol. Lett. 10 1127
Google Scholar
[15] Chiang Y C, Chiou Y P, Chang H C 2002 J. Lightwave Technol. 20 1609
Google Scholar
[16] Sujecki S 2010 Opt. Lett. 35 4115
Google Scholar
[17] Chiou Y P, Du C H 2011 J. Lightwave Technol. 29 3445
Google Scholar
[18] Cao Y 2022 Opt. Express 30 4680
Google Scholar
[19] Berenger J P 1994 J. Comput. Phys. 114 185
Google Scholar
[20] Chew W C, Weedon W H 1994 Microw. Opt. Technol. Lett. 7 599
Google Scholar
[21] Joannopoulos J D, Johnson S G, Winn J N, Meade R D 2008 Photonic Crystals: Molding the Flow of Light (Princeton: Princeton University Press) p20
[22] Press W H, Teukolsky S A, Vetterling W T, Flannery B P 2007 Numerical Recipes: The Art of Scientific Computing (Cambridge: Camebridge University Press) p10
[23] Li Z L, Ito K 2006 The Immersed Interface Method: Numerical Solutions of PDEs Involving Interfaces and Irregular Domains (Philadephia: SIAM) p10
-
图 1 平面波导示意图及坐标系放置
Figure 1. Depiction of a planar waveguide and layout of the coordinate system.
图 2 计算区域离散
Figure 2. Discretization of the computational domain.
图 3 PML吸收边界条件设置示意图
Figure 3. Schematic diagram of the setup of PML absorption boundary conditions.
图 4 收敛曲线, 单界面波导(
$ \text{TM}_\text{s} $ )和对称波导($ \text{TE}_\text{1, 2} $ ) 模式Figure 4. Convergence curves: Modes of single interface waveguide (
$ \text{TM}_\text{s} $ ) and symmetric waveguide ($ \text{TE}_\text{1, 2} $ ).
图 5 收敛曲线, 电磁参数未做处理(-non)和施加调和平均处理(-avg)
Figure 5. Convergence curves: non-averaging (-non) and harmonic averaging (-avg) for electromagnetic parameters.
图 6 收敛曲线: 一维光子晶体波导模式(
$ \text{TE}_\text{c} $ 为包层模式)Figure 6. Convergence curves: Modes of one-dimensional photonic crystal waveguide (
$ \text{TE}_\text{c} $ is cladding mode).
图 7 模场分布: 一维光子晶体波导, 竖直虚线标示界面位置
Figure 7. Distribution of modal fields: One dimensional photonic crystal waveguide, with dashed lines indicating the positions of interfaces.
-
[1] 陈宪锋, 沈小明, 蒋美萍, 金铱 2008 57 3578
Google Scholar
Chen X F, Shen X M, Jiang M P, Jin Y 2008 Acta Phys. Sin. 57 3578
Google Scholar
[2] 陈云天, 王经纬, 陈伟锦, 徐竞 2020 69 154206
Google Scholar
Chen Y T, Wang J W, Chen W J, Xu J 2020 Acta Phys. Sin. 69 154206
Google Scholar
[3] 李慧慧, 薛文瑞, 李宁, 杜易达, 李昌勇 2022 71 108101
Google Scholar
Li H H, Xue W R, Li N, Du Y D, Li C Y 2022 Acta Phys. Sin. 71 108101
Google Scholar
[4] 乔海亮, 王玥, 陈再高, 张殿辉 2013 62 070204
Google Scholar
Qiao H L, Wang Y, Chen Z G, Zhang D H 2013 Acta Phys. Sin. 62 070204
Google Scholar
[5] Wu D, Ohnishi R, Uemura R, Yamaguchi R, Ohnuki S 2018 IEEE Photonics Technol. Lett. 30 1024
Google Scholar
[6] LeVeque R J, Li Z L 1994 SIAM J. Numer. Anal. 31 1019
Google Scholar
[7] LeVeque R J, Li Z L 1995 SIAM J. Numer. Anal. 32 1704
Google Scholar
[8] Horikis T P, Kath W L 2006 Opt. Lett. 31 3417
Google Scholar
[9] Horikis T P 2011 Int. J. Mod. Phys. C 22 687
Google Scholar
[10] Horikis T P 2013 Appl. Math. Model. 37 5080
Google Scholar
[11] Stern M S 1988 IEE Proc. J. (Optoelectron.) 135 56
Google Scholar
[12] Vassallo C 1992 IEE Proc. J. (Optoelectron.) 139 137
Google Scholar
[13] Yamauchi J, Sekiguchi M, Uchiyama O, Shibayama J, Nakano H 1997 IEEE Photonics Technol. Lett. 9 961
Google Scholar
[14] Yamauchi J, Takahashi G, Nakano H 1998 IEEE Photonics Technol. Lett. 10 1127
Google Scholar
[15] Chiang Y C, Chiou Y P, Chang H C 2002 J. Lightwave Technol. 20 1609
Google Scholar
[16] Sujecki S 2010 Opt. Lett. 35 4115
Google Scholar
[17] Chiou Y P, Du C H 2011 J. Lightwave Technol. 29 3445
Google Scholar
[18] Cao Y 2022 Opt. Express 30 4680
Google Scholar
[19] Berenger J P 1994 J. Comput. Phys. 114 185
Google Scholar
[20] Chew W C, Weedon W H 1994 Microw. Opt. Technol. Lett. 7 599
Google Scholar
[21] Joannopoulos J D, Johnson S G, Winn J N, Meade R D 2008 Photonic Crystals: Molding the Flow of Light (Princeton: Princeton University Press) p20
[22] Press W H, Teukolsky S A, Vetterling W T, Flannery B P 2007 Numerical Recipes: The Art of Scientific Computing (Cambridge: Camebridge University Press) p10
[23] Li Z L, Ito K 2006 The Immersed Interface Method: Numerical Solutions of PDEs Involving Interfaces and Irregular Domains (Philadephia: SIAM) p10
DownLoad:
Catalog
Metrics
- Abstract views: 4097
- PDF Downloads: 95
- Cited By: 0
