-
Mode coupling is a common phenomenon in waveguides. The mode coupling among different guided modes in fiber-optic communication can cause crosstalk, and the mode coupling of guided mode and radiated mode can reduce the power of the guided mode. Application of mode coupling can guide the design of optical devices such as couplers and beam splitters with specific functions, which have been widely used in fiber optic communication and fiber sensing. So it is important to analyze how waveguide modes are coupled. The coupled-mode theory is a common method of studying mode coupling in waveguides. It provides not only an intuitive picture of how the photonic modes are hybridized, but also a quantitative assessment of how the hybridization among those relevant modes evolves. In recent years, non-Hermitian waveguides, represented by parity-time symmetrical structures, have become a research hotspot. However the conventional coupled-mode theory no longer works in this case. In this review, we briefly summarize the development history of coupled-mode theory and introduce the representative work in reciprocal waveguide coupled-mode theory in detail. Then the relationship among several coupled-mode theories is analyzed and their applications are briefly introduced.
-
Keywords:
- waveguide /
- mode /
- coupling /
- reciprocity
[1] Pierce J R 1954 J. Appl. Phys. 25 179
Google Scholar
[2] Gould R W 1955 IRE Trans. Electron Devices PGED-2 37
Google Scholar
[3] Louisell W H 1960 Coupled-Mode and Parametric Electronics (New York: Wiley) pp148–225
[4] Miller S E 1954 Bell Syst. Tech. J. 33 661
Google Scholar
[5] Miller S E 1968 Bell Syst. Tech. J. 47 1801
Google Scholar
[6] Miller S E 1969 Bell Syst. Tech. J. 48 2189
Google Scholar
[7] Tang C C H 1969 Advances in Microwaves 4 301
Google Scholar
[8] Schelkunoff S A 1955 Bell Syst. Tech. J. 34 995
Google Scholar
[9] [10] Marcuse D 1971 Bell Syst. Tech. J. 50 1791
Google Scholar
[11] Marcuse D 1973 Bell Syst. Tech. J. 52 817
Google Scholar
[12] Snyder A W 1972 J. Opt. Soc. Am. 62 1267
Google Scholar
[13] Snyder A W 1970 IEEE Trans. Microwave Theory Tech. 18 383
Google Scholar
[14] Yariv A 1973 IEEE J. Quantum Electron. 9 919
Google Scholar
[15] Taylor H F, Yariv A 1974 Proc. IEEE 62 1044
Google Scholar
[16] Kogelnik H 1969 Bell Syst. Tech. J. 48 2909
Google Scholar
[17] McIntyre P D, Snyder A W 1973 J. Opt. Soc. Am. 63 1518
Google Scholar
[18] Yeh C, Manshadi F, Casey K F, Johnston A 1978 J. Opt. Soc. Am. 68 1079
Google Scholar
[19] Dionnet M J F, Shaw H J 1982 IEEE Trans. Microwave Theory Tech. 30 592
Google Scholar
[20] Thyagarajan K, Tewari R 1985 J. Lightwave Technol. 3 59
Google Scholar
[21] Zhang M, Garmire E 1987 J. Lightwave Technol. 5 260
Google Scholar
[22] Elechi C, Yeh C 1973 Opt. Commun. 7 201
Google Scholar
[23] Stoll H, Yariv A 1973 Opt. Commun. 8 5
Google Scholar
[24] Yeh P, Taylor H F 1980 Appl. Opt. 19 2848
Google Scholar
[25] Syms R R A 1985 Appl. Opt. 24 717
Google Scholar
[26] Marcuse D 1987 J. Lightwave Technol. 5 268
Google Scholar
[27] Hardy A, Streifer W 1985 J. Lightwave Technol. 3 1135
Google Scholar
[28] Haus H A, Huang W P, Kawakami S, Whitaker N A 1987 J. Lightwave Technol. 5 16
Google Scholar
[29] Chuang S L 1987 J. Lightwave Technol. 5 5
Google Scholar
[30] El-Ganainy R, Makris K G, Christodoulides D N, Musslimani Z H 2007 Opt. Lett. 32 2632
Google Scholar
[31] Golshani M, Weimann S, Jafari Kh, Khazaei Nezhad M, Langari A, Bahrampour A R, Eichelkraut T, Mahdavi S M, Szameit A 2014 Phys. Rev. Lett. 113 123903
Google Scholar
[32] Klaiman S, Gunther U, Moiseyev N 2008 Phys. Rev. Lett. 101 080402
Google Scholar
[33] Feng L, Xu Y L, Fegadolli W S, Lu M H, Oliveira J E B, Almeida V R, Chen Y F, Scherer A 2013 Nat. Mater. 12 108
Google Scholar
[34] Zhu X, Ramezani H, Shi C, Zhu J, Zhang X 2014 Phys. Rev. X 4 031042
Google Scholar
[35] Lin Z, Ramezani H, Eichelkraut T, Kottos T, Cao H, Christodoulides D N 2011 Phys. Rev. Lett. 106 213901
Google Scholar
[36] Shi Y, Yu Z F, Fan S H 2015 Nat. Photonics 9 388
Google Scholar
[37] Wang X Z 2018 Opt. Lett. 43 5623
Google Scholar
[38] Ruter C E, Makris K G, El-Ganainy R, Christodoulides D N, Segev M, Kip D 2010 Nat. Phys. 6 192
Google Scholar
[39] Hodaei H, Miri M A, Heinrich M, Christodoulides D N, Khajavikhan M 2014 Science 346 975
Google Scholar
[40] Alaeian H, Dionne J A 2014 Phys. Rev. B 89 075136
Google Scholar
[41] Alaeian H, Dionne J A 2014 Phys. Rev. A 89 033829
Google Scholar
[42] Shen Y, Deng X H, Chen L 2014 Opt. Express 22 19440
Google Scholar
[43] Liu Z Z, Zhang Q, Liu X L, Yao Y, Xiao J J 2016 Sci. Rep. 6 22711
Google Scholar
[44] Ke S L, Zhao D, Liu J X, Liu Q J, Liao Q, Wang B, Lu P X 2019 Opt. Express 27 13858
Google Scholar
[45] Peng B, Őzdemir S K, Lei F, Monifi F, Gianfreda M, Long G L, Fan S, Nori F, M.Bender C, Yang L 2014 Nat. Phys. 10 394
Google Scholar
[46] Xu J, Chen Y 2015 Opt. Express 23 22619
Google Scholar
[47] Wu B, Xu J, Xiao J, Chen Y 2016 Opt. Express 24 16566
Google Scholar
[48] Liu Z Z, Zhang Q, Chen Y, Xiao J J 2017 Photonics Res. 5 57
Google Scholar
[49] Wu B, Wang J, Xiao M, Xu J, Chen Y 2017 Opt. Express 25 1040
Google Scholar
[50] Xiong Z F, Chen W J, Wang P, Chen Y T 2017 Opt. Express 25 29822
Google Scholar
[51] Chen W, Xiong Z, Xu J, Chen Y 2019 Phys. Rev. B 99 195307
Google Scholar
[52] Zhang X Q, Chen R S, Zhou Y, Ming H, Wang A T 2016 Chin. Phys. Lett. 33 084201
Google Scholar
[53] 黎磊, 刘桂强, 陈元浩 2013 光学学报 33 0123002
Google Scholar
Li L, Liu G Q, Chen Y H 2013 Acta Opt. Sin. 33 0123002
Google Scholar
[54] 吴立恒, 王明红 2015 光学学报 35 0923003
Google Scholar
Wu L H, Wang M H 2015 Acta Opt. Sin. 35 0923003
Google Scholar
[55] Cai Y J, Li M, Xiong X, Yu L, Ren X F, Guo G P, Guo G C 2015 Chin. Phys. Lett. 32 107305
Google Scholar
[56] 张志东, 赵亚男, 卢东, 熊祖洪, 张中月 2012 61 187301
Google Scholar
Zhang Z D, Zhao Y N, Lu D, Xiong Z H, Zhang Z Y 2012 Acta Phys. Sin. 61 187301
Google Scholar
[57] 王立文, 娄淑琴, 陈卫国, 鹿文亮, 王鑫 2012 61 154207
Google Scholar
Wang L W, Lou S Q, Chen W G, Lu W L, Wang X 2012 Acta Phys. Sin. 61 154207
Google Scholar
[58] Xu J, Wu B, Chen Y T 2015 Opt. Express 23 11566
Google Scholar
[59] Sakurai J J, Tuan S F 1994 Modern Quantum Mechanics (Rev. Ed.) (Reading, Mass.: Addison-Wesley Pub. Co.) pp71–73
[60] Rumsey V H 1954 Phys. Rev. 94 1483
Google Scholar
[61] Moiseyev N 2011 Non-Hermitian Quantum Mechanics (New York: Cambridge University Press) pp174–210
[62] Collin R E 1960 Field Theory of Guided Waves (New York: The Maple Press) p231
[63] McIsaac P R 1991 IEEE Trans. Microwave Theory Tech. 39 1808
Google Scholar
[64] Villeneuve A T 1959 IEEE Trans. Microwave Theory Tech. 7 441
Google Scholar
[65] Silvestre E, Abián M A, Gimeno B, Ferrando A, Andrés M V, Boria V E 2000 IEEE Trans. Microwave Theory Tech. 48 589
Google Scholar
[66] Snyder A W, Love J D 1983 Optical Waveguide Theory (New York: Springer Science & Business Media) pp214–216
[67] Zhu Y, Cangellaris A C 2006 Multigrid Finite Element Methods for Electromagnetic Field Modeling (Hoboken, N.J.: Wiley-IEEE Press) pp244–249
[68] 钱景仁 2009 光学学报 29 1188
Qian J R 2009 Acta Opt. Sin. 29 1188
[69] Liu H, Lalanne P 2008 Nature 452 728
Google Scholar
[70] Chen Y T, Zhang R Y, Xiong Z F, Hang Z H, Li J S, Shen J Q, Chan C T 2019 Nat. Commun. 10 3125
Google Scholar
[71] Shi H K, Xiong Z F, Chen W J, Xu J, Wang S B, Chen Y T 2019 Opt. Express 27 28114
Google Scholar
[72] Bender C M, Boettcher S, Meisinger P N 1999 J. Math. Phys. 40 2201
Google Scholar
[73] Bernevig B A, Hughes T L 2013 Topological Insulators and Topological Superconductors (Princeton: Princeton University Press) pp30–40
-
图 1 前向和后向传播模式之间对称关系 (a) 手征对称; (b) 时间反演对称; (c) 宇称对称
Figure 1. Symmetry relations between the forward and backward propagating modes: (a) Chiral symmetry; (b) time reversal symmetry; (c) parity symmetry.
图 2 有效折射率
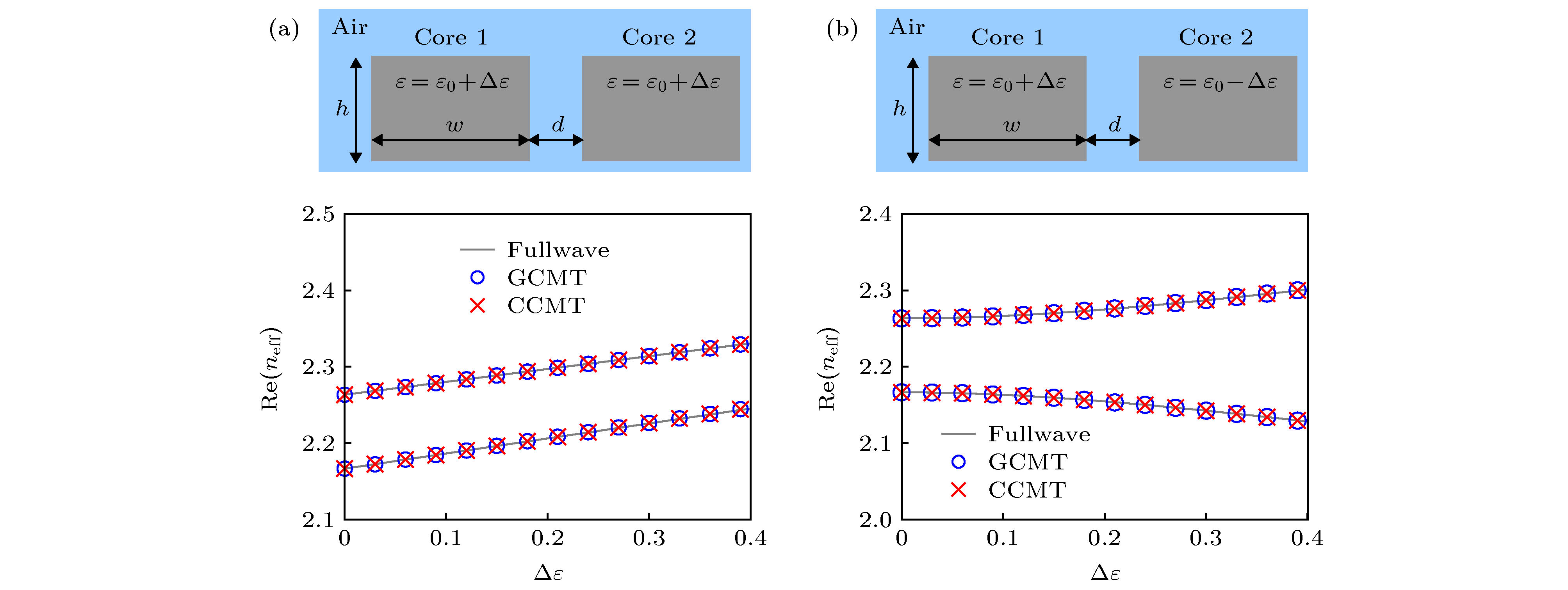
$n_{\rm{eff}}$ 实部与$\Delta {{\varepsilon}} $ (a) 纤芯1 相对介电常数为${{\varepsilon}}= {{\varepsilon}}_0 + \Delta {{\varepsilon}} $ , 纤芯2 相对介电常数为${{\varepsilon}}= {{\varepsilon}}_0 + \Delta {{\varepsilon}} $ ; (b) 纤芯1 相对介电常数为${{\varepsilon}}= {{\varepsilon}}_0 + \Delta {{\varepsilon}} $ , 纤芯2 相对介电常数为${{\varepsilon}}= {{\varepsilon}}_0 - \Delta {{\varepsilon}} $ Figure 2. Real part of effective mode indices
$n_{\rm{eff}}$ versus$\Delta {{\varepsilon}} $ : (a)${{\varepsilon}}= {{\varepsilon}}_0 + \Delta {{\varepsilon}} $ in core layer 1 and${{\varepsilon}}= {{\varepsilon}}_0 + \Delta {{\varepsilon}} $ in core layer 2; (b)${{\varepsilon}}= {{\varepsilon}}_0 + \Delta {{\varepsilon}} $ in core layer 1 and${{\varepsilon}}= {{\varepsilon}}_0 - \Delta {{\varepsilon}} $ in core layer 2.
图 3 有效折射率
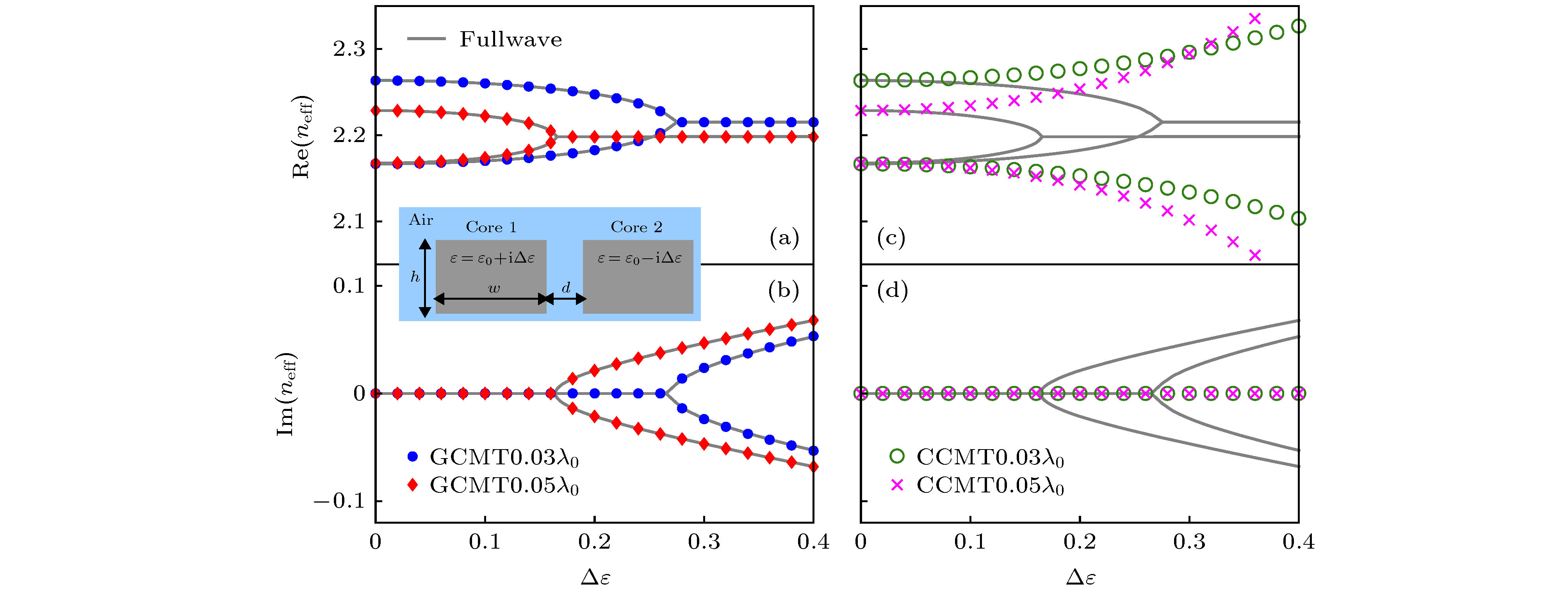
$n_{\rm{eff}}$ 实部与虚部及$\Delta {{\varepsilon}} $ (a), (c) 有效折射率$n_{\rm{eff}}$ 实部; (b), (d) 有效折射率$n_{\rm{eff}}$ 虚部Figure 3. Real part and imaginary part of effective mode indices
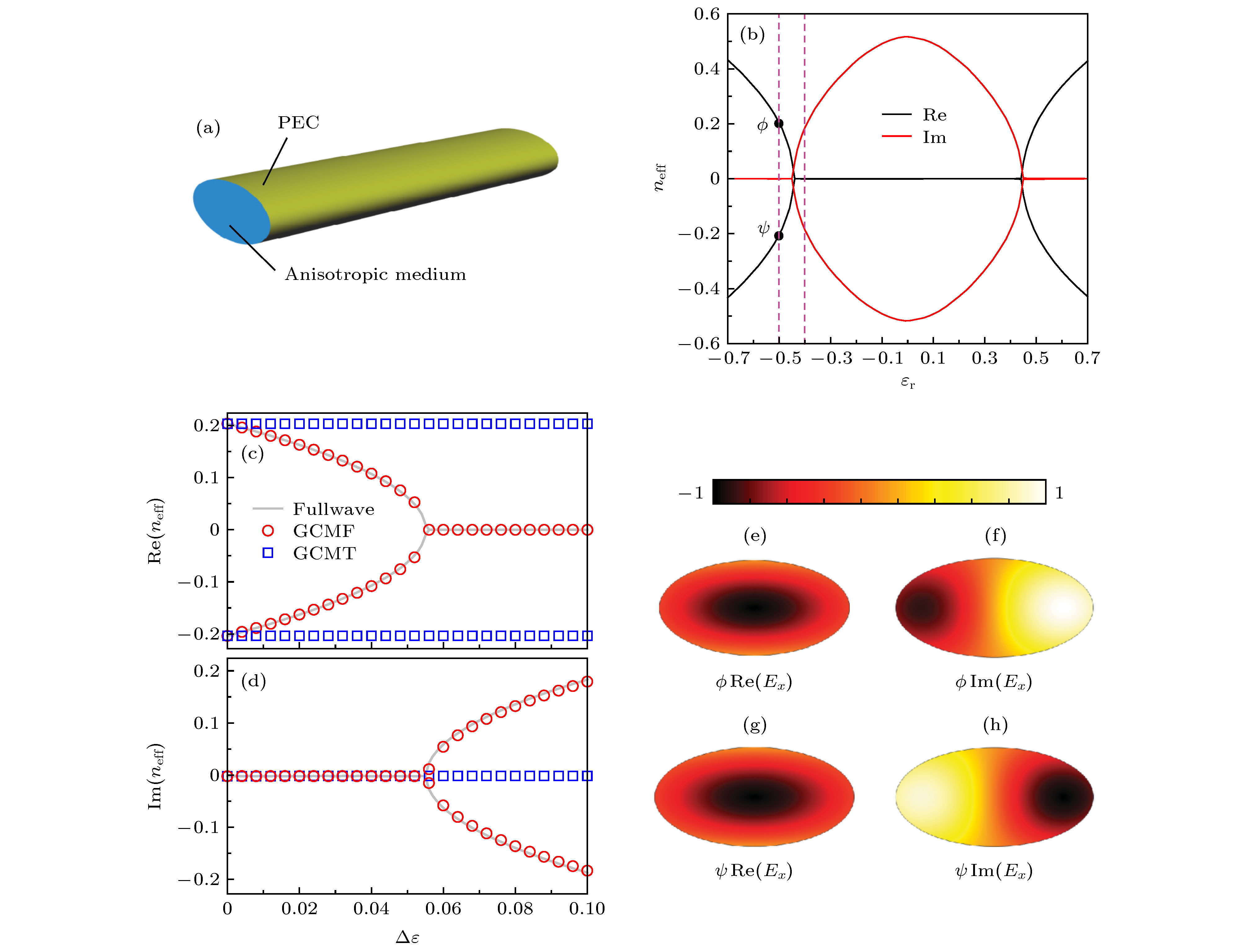
$n_{\rm{eff}}$ versus$\Delta {{\varepsilon}} $ : (a), (c) Real part of effective mode indices$n_{\rm{eff}}$ ; (b), (d) imaginary part of effective mode indices$n_{\rm{eff}}$ .
图 4 各向异性波导 (a) 椭圆波导示意图; (b) 使用有限元法进行全波计算得到的有效折射率
$n_{\rm{eff}}$ 实部(红线)和虚部(黑线)与${{\varepsilon}}_{\rm{r}}$ 函数关系; (c)有效折射率$n_{\rm{eff}}$ 实部; (d) 有效折射率$n_{\rm{eff}}$ 虚部; (e)—(h) 图(b)中黑色实心圆标记点前向/后向传播模式$\phi$ 的$E_x$ 分量的实部/虚部Figure 4. Anisotropic waveguide: (a) The schematic of elliptical waveguide; (b) the real (red line) and imaginary (black line) part of effective modal indices, calculated from fullwave simulation using finite element method, as a function of
${{\varepsilon}}_{\rm{r}}$ ; (c) real part of effective mode indices$n_{\rm{eff}}$ ; (d) imaginary part of effective mode indices$n_{\rm{eff}}$ ; (e)−(h) the real/imaginary part of$E_x$ obtained from fullwave simulation is shown for the modes$\phi$ 表 1 当
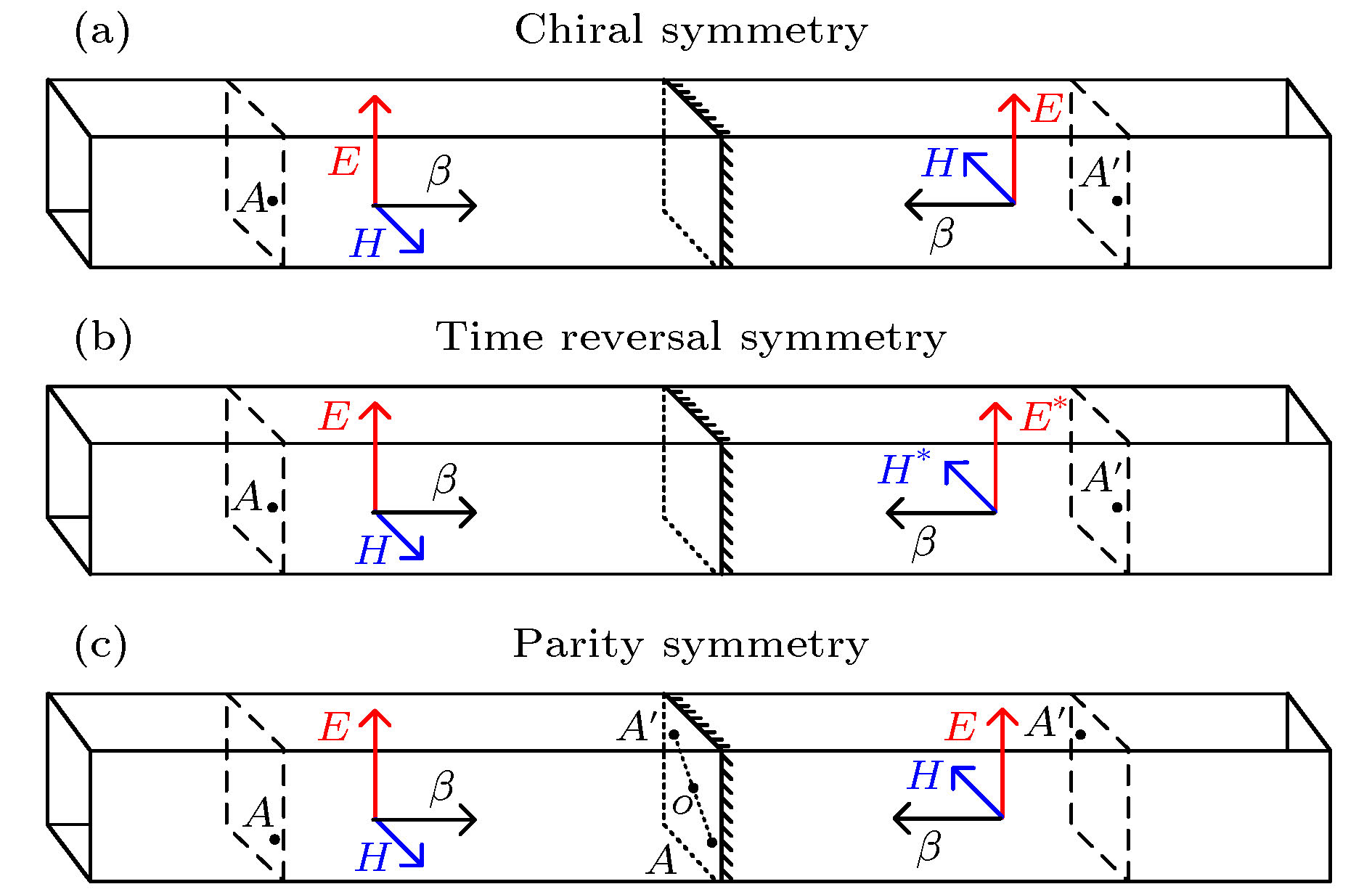
$\beta_i > 0$ 时, 互易波导中原始场和伴随场之间的对称关系Table 1. Symmetric relation of original field and adjoint field in the reciprocal waveguides with
$\beta_i > 0$ $\beta_i$对应的模式 $-\beta_i$对应的模式 $({\bar{{L}}}, {\bar{{B}}})$ $\left[\beta_i, {{\phi}}_i\right]$ $\left[-\beta_i, {{\psi}}_i\right]$ $({\bar{{L}}}^{\rm{a}}, {\bar{{B}}}^{\rm{a}})$ $\left[\beta_i, {{\psi}}_i\right]$ $\left[-\beta_i, {{\phi}}_i\right]$ 
DownLoad: CSV
表 2 互易波导中原始场和伴随场之间的对称关系
Table 2. Symmetry relations of original field and adjoint field in the reciprocal waveguides.
对称关系 算符 对称性关系 约束条件 手征对称 ${\sigma}$ ${{{\psi}}}_i({{r}}) = {\bar{\sigma}}{{{\phi}}}_i({{r}})$ ${{{\varepsilon}}}_{\rm r}^{zt} = {{{\varepsilon}}}_{\rm r}^{tz} = 0$, ${{{\mu}}}_{\rm r}^{zt} = {{{\mu}}}_{\rm r}^{tz} = 0$和${\bar{ \chi}} = 0$ 时间反演对称 ${\cal{T}}$ ${{{\psi}}}_i({{r}}) = {\bar{\sigma}}({{{\phi}}}_i({{r}}))^*$ ${\bar{{{\varepsilon}}}}_{\rm r}$, ${\bar{{{\mu}}}}_{\rm r}$和${\bar{ \chi}}$是实数 宇称对称 ${\cal{P}}$ ${{{\psi}}}_i({{r}}) = {\bar{\sigma}}{{{\phi}}}_i(-{{r}})$ ${\bar{{{\varepsilon}}}}_{\rm r}({{r}}) = {\bar{{{\varepsilon}}}}_{\rm r}(-{{r}})$, ${\bar{{{\mu}}}}_{\rm r}({{r}}) = {\bar{{{\mu}}}}_{\rm r}(-{{r}})$和 ${\bar{ \chi}}({{r}}) = -{\bar{ \chi}}(-{{r}})$
DownLoad: CSV
表 3 CCMT, GCMT和GCMF之间比较
Table 3. Comparison between CCMT, GCMT and GCMF.
模式耦合理论 传统模式耦合理论(CCMT) 手征对称模式耦合理论(GCMT) 广义模式耦合理论(GCMF) 耦合模式展开式形式 $\varPhi =\displaystyle \sum a_i\phi _i$ $\varPhi = \displaystyle\sum a_i\phi _i$ $\varPhi = \displaystyle\sum a_i\phi _i ^+ +b_i \psi _i ^-$ 守恒量 光功率守恒
$\nabla \left({{{{E}}} _1 \times {{{H}}} _2 ^{\ast}} + {{{E}}} _2 ^{\ast} \times {{{H}}}_1\right) = 0$作用量守恒
$\nabla \left({{{{E}}} _1 \times {{{H}}} _2 } + {{{E}}} _2 \times {{{H}}}_1\right) = 0$作用量守恒
$\nabla \left({{{{E}}} _1 \times {{{H}}} _2 } + {{{E}}} _2 \times {{{H}}}_1\right) = 0$测试函数 $\phi _j ^{\ast} $ $\sigma \phi _j$ $ \psi _j ^+$, $\psi _j ^-$ 本征方程 ${\bar{{L}}}{{\phi}}_i = \beta_i {\bar{{B}}}{{\phi}}_i $ ${\bar{{L}}}{{\phi}}_i = \beta_i {\bar{{B}}}{{\phi}}_i $ ${\bar{{L}}}{{\phi}}_i = \beta_i {\bar{{B}}}{{\phi}}_i$ 测试函数进行测试 $\displaystyle\iiint \phi _j ^{\ast} [{\bar{{L} } }{{\phi} }_i-\beta_i {\bar{{B} } }{{\phi} }_i]{\rm{d} }v \!=\! 0$ $\displaystyle\iiint \sigma \phi _j [{\bar{{L} } }{{\phi} }_i-\beta_i {\bar{{B} } }{{\phi} }_i]{\rm{d} }v \!=\! 0$ $\displaystyle\iiint \psi _j \cdot [{\bar{{L} } }{{\phi} }_i \!-\! \beta_i {\bar{{B} } }{{\phi} }_i]{\rm{d} }v \!=\! 0$
DownLoad: CSV
-
[1] Pierce J R 1954 J. Appl. Phys. 25 179
Google Scholar
[2] Gould R W 1955 IRE Trans. Electron Devices PGED-2 37
Google Scholar
[3] Louisell W H 1960 Coupled-Mode and Parametric Electronics (New York: Wiley) pp148–225
[4] Miller S E 1954 Bell Syst. Tech. J. 33 661
Google Scholar
[5] Miller S E 1968 Bell Syst. Tech. J. 47 1801
Google Scholar
[6] Miller S E 1969 Bell Syst. Tech. J. 48 2189
Google Scholar
[7] Tang C C H 1969 Advances in Microwaves 4 301
Google Scholar
[8] Schelkunoff S A 1955 Bell Syst. Tech. J. 34 995
Google Scholar
[9] [10] Marcuse D 1971 Bell Syst. Tech. J. 50 1791
Google Scholar
[11] Marcuse D 1973 Bell Syst. Tech. J. 52 817
Google Scholar
[12] Snyder A W 1972 J. Opt. Soc. Am. 62 1267
Google Scholar
[13] Snyder A W 1970 IEEE Trans. Microwave Theory Tech. 18 383
Google Scholar
[14] Yariv A 1973 IEEE J. Quantum Electron. 9 919
Google Scholar
[15] Taylor H F, Yariv A 1974 Proc. IEEE 62 1044
Google Scholar
[16] Kogelnik H 1969 Bell Syst. Tech. J. 48 2909
Google Scholar
[17] McIntyre P D, Snyder A W 1973 J. Opt. Soc. Am. 63 1518
Google Scholar
[18] Yeh C, Manshadi F, Casey K F, Johnston A 1978 J. Opt. Soc. Am. 68 1079
Google Scholar
[19] Dionnet M J F, Shaw H J 1982 IEEE Trans. Microwave Theory Tech. 30 592
Google Scholar
[20] Thyagarajan K, Tewari R 1985 J. Lightwave Technol. 3 59
Google Scholar
[21] Zhang M, Garmire E 1987 J. Lightwave Technol. 5 260
Google Scholar
[22] Elechi C, Yeh C 1973 Opt. Commun. 7 201
Google Scholar
[23] Stoll H, Yariv A 1973 Opt. Commun. 8 5
Google Scholar
[24] Yeh P, Taylor H F 1980 Appl. Opt. 19 2848
Google Scholar
[25] Syms R R A 1985 Appl. Opt. 24 717
Google Scholar
[26] Marcuse D 1987 J. Lightwave Technol. 5 268
Google Scholar
[27] Hardy A, Streifer W 1985 J. Lightwave Technol. 3 1135
Google Scholar
[28] Haus H A, Huang W P, Kawakami S, Whitaker N A 1987 J. Lightwave Technol. 5 16
Google Scholar
[29] Chuang S L 1987 J. Lightwave Technol. 5 5
Google Scholar
[30] El-Ganainy R, Makris K G, Christodoulides D N, Musslimani Z H 2007 Opt. Lett. 32 2632
Google Scholar
[31] Golshani M, Weimann S, Jafari Kh, Khazaei Nezhad M, Langari A, Bahrampour A R, Eichelkraut T, Mahdavi S M, Szameit A 2014 Phys. Rev. Lett. 113 123903
Google Scholar
[32] Klaiman S, Gunther U, Moiseyev N 2008 Phys. Rev. Lett. 101 080402
Google Scholar
[33] Feng L, Xu Y L, Fegadolli W S, Lu M H, Oliveira J E B, Almeida V R, Chen Y F, Scherer A 2013 Nat. Mater. 12 108
Google Scholar
[34] Zhu X, Ramezani H, Shi C, Zhu J, Zhang X 2014 Phys. Rev. X 4 031042
Google Scholar
[35] Lin Z, Ramezani H, Eichelkraut T, Kottos T, Cao H, Christodoulides D N 2011 Phys. Rev. Lett. 106 213901
Google Scholar
[36] Shi Y, Yu Z F, Fan S H 2015 Nat. Photonics 9 388
Google Scholar
[37] Wang X Z 2018 Opt. Lett. 43 5623
Google Scholar
[38] Ruter C E, Makris K G, El-Ganainy R, Christodoulides D N, Segev M, Kip D 2010 Nat. Phys. 6 192
Google Scholar
[39] Hodaei H, Miri M A, Heinrich M, Christodoulides D N, Khajavikhan M 2014 Science 346 975
Google Scholar
[40] Alaeian H, Dionne J A 2014 Phys. Rev. B 89 075136
Google Scholar
[41] Alaeian H, Dionne J A 2014 Phys. Rev. A 89 033829
Google Scholar
[42] Shen Y, Deng X H, Chen L 2014 Opt. Express 22 19440
Google Scholar
[43] Liu Z Z, Zhang Q, Liu X L, Yao Y, Xiao J J 2016 Sci. Rep. 6 22711
Google Scholar
[44] Ke S L, Zhao D, Liu J X, Liu Q J, Liao Q, Wang B, Lu P X 2019 Opt. Express 27 13858
Google Scholar
[45] Peng B, Őzdemir S K, Lei F, Monifi F, Gianfreda M, Long G L, Fan S, Nori F, M.Bender C, Yang L 2014 Nat. Phys. 10 394
Google Scholar
[46] Xu J, Chen Y 2015 Opt. Express 23 22619
Google Scholar
[47] Wu B, Xu J, Xiao J, Chen Y 2016 Opt. Express 24 16566
Google Scholar
[48] Liu Z Z, Zhang Q, Chen Y, Xiao J J 2017 Photonics Res. 5 57
Google Scholar
[49] Wu B, Wang J, Xiao M, Xu J, Chen Y 2017 Opt. Express 25 1040
Google Scholar
[50] Xiong Z F, Chen W J, Wang P, Chen Y T 2017 Opt. Express 25 29822
Google Scholar
[51] Chen W, Xiong Z, Xu J, Chen Y 2019 Phys. Rev. B 99 195307
Google Scholar
[52] Zhang X Q, Chen R S, Zhou Y, Ming H, Wang A T 2016 Chin. Phys. Lett. 33 084201
Google Scholar
[53] 黎磊, 刘桂强, 陈元浩 2013 光学学报 33 0123002
Google Scholar
Li L, Liu G Q, Chen Y H 2013 Acta Opt. Sin. 33 0123002
Google Scholar
[54] 吴立恒, 王明红 2015 光学学报 35 0923003
Google Scholar
Wu L H, Wang M H 2015 Acta Opt. Sin. 35 0923003
Google Scholar
[55] Cai Y J, Li M, Xiong X, Yu L, Ren X F, Guo G P, Guo G C 2015 Chin. Phys. Lett. 32 107305
Google Scholar
[56] 张志东, 赵亚男, 卢东, 熊祖洪, 张中月 2012 61 187301
Google Scholar
Zhang Z D, Zhao Y N, Lu D, Xiong Z H, Zhang Z Y 2012 Acta Phys. Sin. 61 187301
Google Scholar
[57] 王立文, 娄淑琴, 陈卫国, 鹿文亮, 王鑫 2012 61 154207
Google Scholar
Wang L W, Lou S Q, Chen W G, Lu W L, Wang X 2012 Acta Phys. Sin. 61 154207
Google Scholar
[58] Xu J, Wu B, Chen Y T 2015 Opt. Express 23 11566
Google Scholar
[59] Sakurai J J, Tuan S F 1994 Modern Quantum Mechanics (Rev. Ed.) (Reading, Mass.: Addison-Wesley Pub. Co.) pp71–73
[60] Rumsey V H 1954 Phys. Rev. 94 1483
Google Scholar
[61] Moiseyev N 2011 Non-Hermitian Quantum Mechanics (New York: Cambridge University Press) pp174–210
[62] Collin R E 1960 Field Theory of Guided Waves (New York: The Maple Press) p231
[63] McIsaac P R 1991 IEEE Trans. Microwave Theory Tech. 39 1808
Google Scholar
[64] Villeneuve A T 1959 IEEE Trans. Microwave Theory Tech. 7 441
Google Scholar
[65] Silvestre E, Abián M A, Gimeno B, Ferrando A, Andrés M V, Boria V E 2000 IEEE Trans. Microwave Theory Tech. 48 589
Google Scholar
[66] Snyder A W, Love J D 1983 Optical Waveguide Theory (New York: Springer Science & Business Media) pp214–216
[67] Zhu Y, Cangellaris A C 2006 Multigrid Finite Element Methods for Electromagnetic Field Modeling (Hoboken, N.J.: Wiley-IEEE Press) pp244–249
[68] 钱景仁 2009 光学学报 29 1188
Qian J R 2009 Acta Opt. Sin. 29 1188
[69] Liu H, Lalanne P 2008 Nature 452 728
Google Scholar
[70] Chen Y T, Zhang R Y, Xiong Z F, Hang Z H, Li J S, Shen J Q, Chan C T 2019 Nat. Commun. 10 3125
Google Scholar
[71] Shi H K, Xiong Z F, Chen W J, Xu J, Wang S B, Chen Y T 2019 Opt. Express 27 28114
Google Scholar
[72] Bender C M, Boettcher S, Meisinger P N 1999 J. Math. Phys. 40 2201
Google Scholar
[73] Bernevig B A, Hughes T L 2013 Topological Insulators and Topological Superconductors (Princeton: Princeton University Press) pp30–40
DownLoad:
Catalog
Metrics
- Abstract views: 17766
- PDF Downloads: 675
- Cited By: 0
