-
Owing to the unique physical characteristics of Rydberg atoms, which play an important role in quantum information and quantum computation, the theoretical and applied research of Rydberg atoms have become the hot spots of scientific research in recent years. With the large polarizability of Rydberg atoms, even a small electric field could cause a considerable electric dipole moment, resulting in a strong dipole-dipole interaction between Rydberg atoms. The multiple excitations of the Rydberg states are strongly inhibited because of the strong dipole interaction between atoms within a mesoscopic interaction (blockade) region. We call this phenomenon the dipole blockade effect. The dipole blockade effect makes it possible to build single-photon quantum devices, implement quantum gates, generate quantum entanglement, and simulate many-body quantum problems, etc. A Rydberg atomic ensemble in the same blockade region can be regarded as a superatom. In the same way, if these atoms trapped in two optical dipole traps, each sub-ensemble can be considered as a sub-superatom which is closely related to the superatom. According to the fact that two Rydberg sub-superatoms can be strongly correlated due to sharing no more than one excited Rydberg atom, we study correlated collective excitation and quantum entanglement between two Rydberg sub-superatoms in a steady state. With the superatom model, the problem of exponentially increasing system size with the number of atoms can be circumvented to a certain extent in studying many-body physics. By solving the two-body Lindblad’s master equation accurately, we obtain the analytical expressions for the collective excitation probabilities of the two sub-superatoms, and the concurrence measuring the bipartite entanglement between them. Our results show that they are all sensitive to the number of atoms in each Rydberg superatom: the bigger (including more atoms) the Rydberg superatom, the higher the collective Rydberg excitation probability is. And that the maximally entangled state can only be obtained with two equal-sized Rydberg superatoms. When this condition is fulfilled, the mesoscopic entanglement can be generated by adding the number of atoms in each Rydberg superatom. This may provide an attractive platform for studying the quantum-classical correspondence and have potential promising applications in quantum information processing. -
Keywords:
- Rydberg atom /
- dipole blockade /
- superatom /
- Rydberg collective excitation /
- quantum entanglement
[1] Martin G 2015 Phys. Rev. A 92 013629
Google Scholar
[2] Zhou M T, Liu J T, Sun P F, An Z Y, Li J, Bao X H, Pan J W 2020 Phys. Rev. A 102 013706
Google Scholar
[3] Pitalúa-García D 2013 Phys. Rev. Lett. 110 210402
Google Scholar
[4] Rao D D B, Klaus M 2014 Phys. Rev. A 89 030301
Google Scholar
[5] Gorniaczyk H, Tresp C, Schmidt J, Fedder H, Hofferberth S 2014 Phys. Rev. Lett. 113 053601
Google Scholar
[6] David P, Georgios M N 2014 Phys. Rev. A 89 013419
Google Scholar
[7] Li D X, Shao X Q 2018 Phys. Rev. A 98 062338
Google Scholar
[8] Mario B, Fernando G, Brandão S L 2018 Phys. Rev. Lett. 121 040504
Google Scholar
[9] Feng D, Hu X Y 2020 Phys. Rev. A 102 042404
Google Scholar
[10] Dong Y, Zhang S Y, Wang Y, Duan L M, Deng D L 2022 Phys. Rev. R 4 023095
Google Scholar
[11] Zhang C H, Peter G, Wolynes, Martin G 2022 Phys. Rev. A 105 033322
Google Scholar
[12] Parmee C D, Cooper N R 2018 Phys. Rev. A 97 053616
Google Scholar
[13] Bhaktavatsala R D D, Klaus M 2014 Phys. Rev. A 90 062319
Google Scholar
[14] Thomas M, Ivana V, Michael J H, Walter H 2016 Phys. Rev. A 94 013809
Google Scholar
[15] Soriente M, Donner T, Chitra R, Zilberberg O 2018 Phys. Rev. Lett. 120 183603
Google Scholar
[16] Stanojevic J, Côté R 2009 Phys. Rev. A 80 033418
Google Scholar
[17] Johannes Z, Peter S, Sebastian H 2015 Phys. Rev. X 5 031015
Google Scholar
[18] Fabian L 2017 New J. Phys. 19 113014
Google Scholar
[19] Zhao P Z, Wu X, Xing T H, Xu G F, Tong D M 2018 Phys. Rev. A 98 032313
Google Scholar
[20] Asaf P, Christoph B, Jan K, Christoph T, Ivan M 2017 Phys. Rev. X 7 041010
Google Scholar
[21] Luo Y H, Zhong H S, Manuel E, Wang X L, Peng L, Mario K, Xiao J, Li L, Liu N L, Lu C Y, Anton Z, Pan J W 2019 Phys. Rev. Lett. 123 070505
Google Scholar
[22] Nicolas G, Grégoire R, Wolfgang T, Hugo Z 2002 Rev. Mod. Phys. 74 145
Google Scholar
[23] Scarani V, Bechmann-Pasquinucci H, Cerf N J, Dušek M, Lütkenhaus N, Peev M 2009 Rev. Mod. Phys. 81 1301
Google Scholar
[24] Damian M, Barry C S 2008 Phys. Rev. A 78 042309
Google Scholar
[25] Zhu A D, Xia Y, Fan Q B, Zhang S 2006 Phys. Rev. A 73 022338
Google Scholar
[26] Li X H, Deng F G, Zhou H Y 2006 Phys. Rev. A 74 054302
Google Scholar
[27] Li T, Long G L 2020 New J Phys. 22 063017
Google Scholar
[28] Robert R, Daniel E, Browne Hans J, Briegel 2003 Phys. Rev. A 68 022312
Google Scholar
[29] James A P, Zhang Y T, Gennady P B, Sabre K 2013 Phys. Rev. E 87 062704
Google Scholar
[30] Li T, Yin Z Q 2016 Sci. Bull. 61 163
Google Scholar
[31] Horodecki R, Horodecki P, Horodecki M, Horodecki K 2009 Rev. Mo. Phys. 81 865
Google Scholar
[32] Deng D L, Li X, Das Sarma S 2017 Phys. Rev. X 7 021021
Google Scholar
[33] Ji Y Q, Liu Y L, Zhou S J, Xiu X M, Dong L, Dong H K, Gao Y J, Yi X X 2019 Phys. Rev. A 99 023808
Google Scholar
[34] Wang T J, Lu Y, Long G L 2012 Phys. Rev. A 86 042337
Google Scholar
[35] Kiesel N, Schmid C, Tóth G, Solano E, Weinfurter H 2007 Phys. Rev. Lett. 98 063604
Google Scholar
[36] Nicolas L 2016 Phys. Rep. 6 008
Google Scholar
[37] Maksym K, Cao J S 2005 Phys. Rev. Lett. 95 180405
Google Scholar
[38] Salcedo L L 2012 Phys. Rev. A 85 022127
Google Scholar
[39] Yan D, Bai W J, Bai J N, Chen L, Han H Y, Wu J H 2022 Photonics 9 242
Google Scholar
-
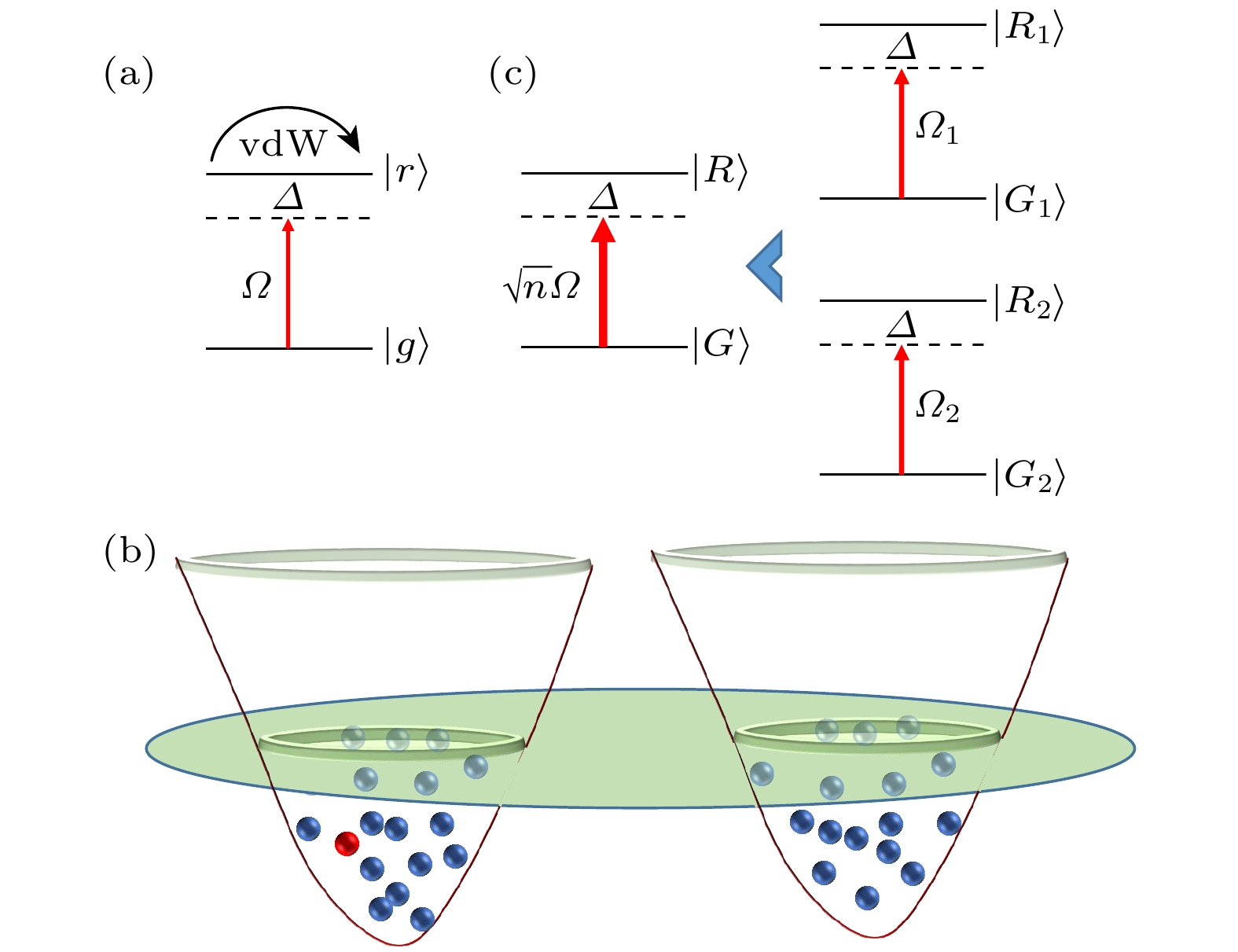
图 1 (a)二能级里德伯原子的能级结构. 基态
$ \left| g \right\rangle $ 和里德伯态$ \left| r \right\rangle $ 通过单模激光场($ \varOmega $ 为拉比频率;$ \varDelta $ 为单光子失谐)耦合, 两个同时激发到里德伯态的原子之间存在范德瓦耳斯势(vdW)相互作用. (b)处于同一偶极阻塞区域但是捕获在两个光偶极阱中的原子系综最多共享一个里德伯原子(红色小球). (c)里德伯超级原子的能级结构. 整个原子系综可以看作一个里德伯超级原子(左图), 而两个光偶极阱中的子原子系综(原子数目分别为$ {n_1} $ 和$ {n_2} $ )可以看作是较小的两个亚里德伯超级原子(右图). 右图中有效拉比频率分别为${\varOmega _1} = $ $ \sqrt {{n_1}} ( {1 - \langle {{{\hat \varSigma }_{{R_2}{R_2}}}} \rangle } )\varOmega$ 和${\varOmega _2} = \sqrt {{n_2}} ( {1 - \langle {{{\hat \varSigma }_{{R_1}{R_1}}}} \rangle } )\varOmega$ , 这里$ \left\langle \cdot \right\rangle $ 代表任意量子态的平均值Figure 1. (a) Level structure of a two-level Rydberg atom, the ground state
$ \left| g \right\rangle $ and the Rydberg state$ \left| r \right\rangle $ are coupled by the single-mode field with Rabi frequency$ \varOmega $ and single-photon detuning$ \varDelta $ . Two Rydberg atoms interact via a van der Waals (vdW) potential. (b) All atoms are loaded in two optical dipole traps but in the same the blockade region represented by big green circle. The red pellet denotes an atom excited to the Rydberg state. (c) Level structures of a superatom containing$ n $ atoms and a sub superatom containing$ {n_1} $ ($ {n_2} $ ) atoms, respectively. They represent the whole atomic ensemble, and the sub-ensemble of$ {n_1} $ ($ {n_2} $ ) atoms trapped in one optical dipole trap.
图 2
$ \varOmega /\gamma = 2.0 $ ,$ \varDelta = 0 $ 时, 稳态超级原子和亚超级原子激发概率$ P $ ,$ {P_1} $ ,$ {P_2} $ 以及并发纠缠C作为(a)亚超级原子中数目$ {n_1} $ ($ n = {n_1} + {n_2} = 42 $ 保持不变)和(b)总原子数$ n $ (其$ {n_2} - {n_1} = 1 $ 保持不变)的函数Figure 2. Steady-state excitation probabilities of superatoms, sub-superatom
$ P $ ,$ {P_1} $ ,$ {P_2} $ and the concurrence C as a function of the number$ {n_1} $ for fixed$ n = {n_1} + {n_2} = 42 $ (a) and the total number$ n $ of atoms for fixed$ {n_2} - {n_1} = 1 $ (b) with$ \varOmega /\gamma = 2.0 $ ,$ \varDelta = 0 $ .
图 3
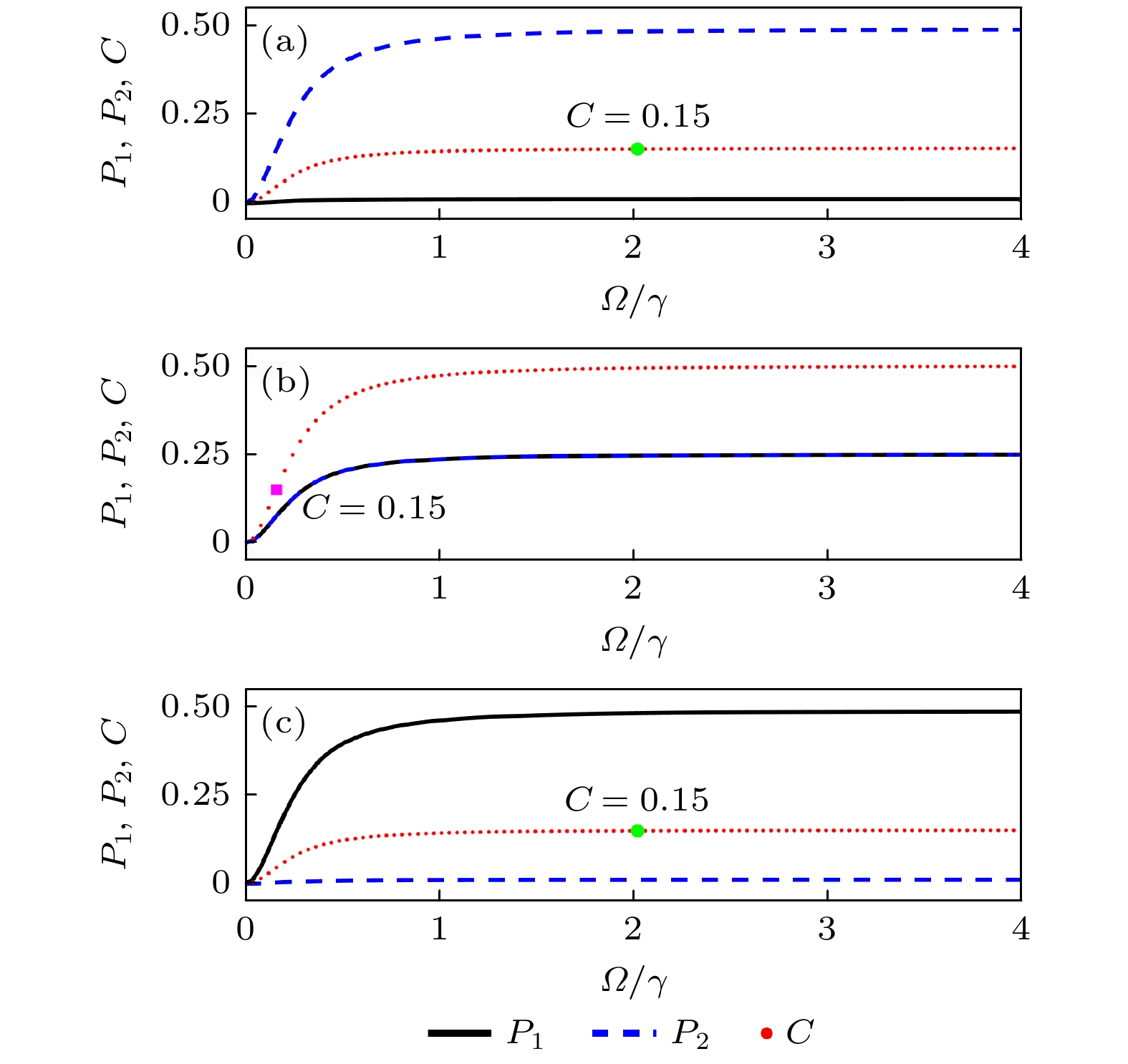
$ \varDelta = 0 $ 时, 稳态亚超级原子激发概率$ {P_1} $ ,$ {P_2} $ 以及并发纠缠C作为$ \varOmega /\gamma $ 的函数(绿色实心圆点和粉色正方形点代表$ C = 0.15 $ ) (a)$ {n_1} = 1 $ ,$ {n_2} = 41 $ ; (b)$ {n_1} = 21 $ ,$ {n_2} = 21 $ ; (c)$ {n_1} = 41 $ ,$ {n_2} = 1 $ Figure 3. Steady-state excitation probabilities of sub-superatoms
$ {P_1} $ ,$ {P_2} $ and the concurrence C as a function of$ \varOmega /\gamma $ with$ \varDelta = 0 $ : (a)$ {n_1} = 1 $ ,$ {n_2} = 41 $ ; (b)$ {n_1} = 21 $ ,${n_2} = $ $ 21$ ; (c)$ {n_1} = 41 $ ,$ {n_2} = 1 $ .
图 4
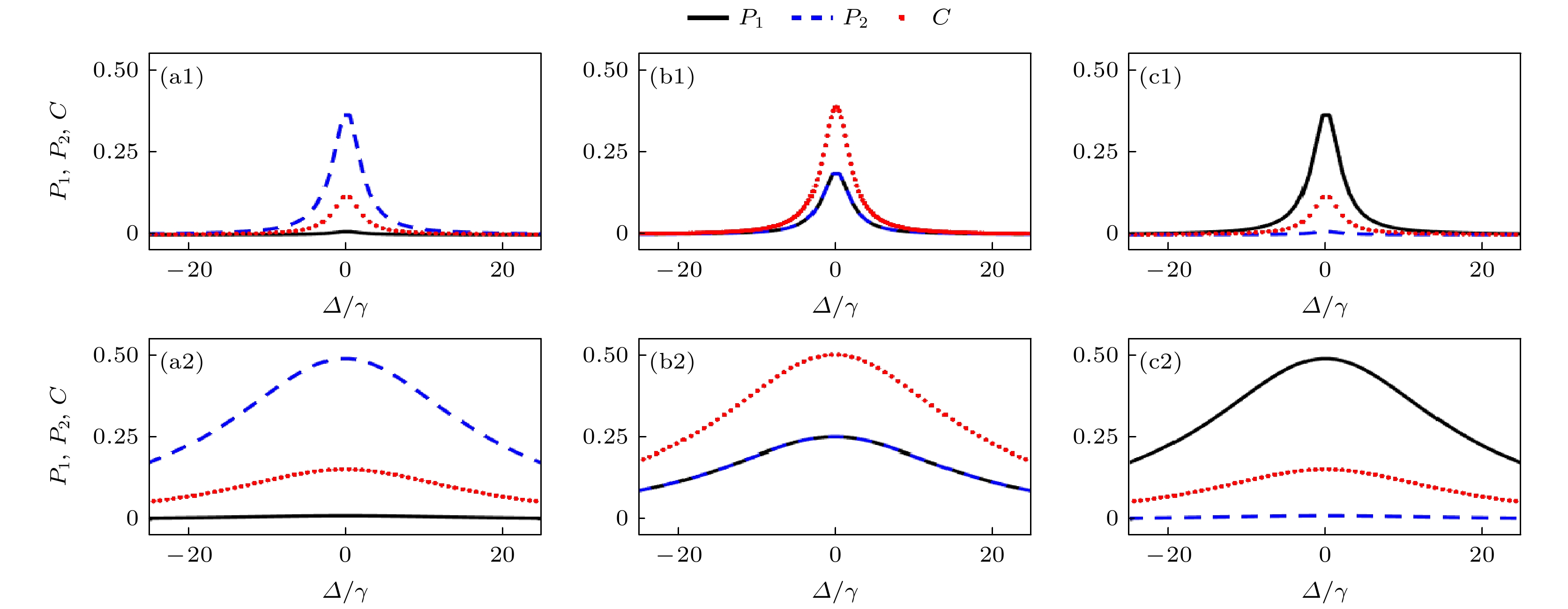
$ \varOmega /\gamma = 0.2 $ (第一行)和$ \varOmega /\gamma = 2 $ (第二行)下, 稳态亚超级原子激发概率$ {P_1} $ ,$ {P_2} $ 以及并发纠缠$ C $ 作为$ \varDelta /\gamma $ 的函数 (a1), (a2)$ {n_1} = 1 $ ,$ {n_2} = 41 $ ; (b1), (b2)$ {n_1} = 21 $ ,$ {n_2} = 21 $ ; (c1), (c2)$ {n_1} = 41 $ ,$ {n_2} = 1 $ Figure 4. Steady-state excitation probabilities of sub-superatoms
$ {P_1} $ ,$ {P_2} $ and the concurrence$ C $ as a function of$ \varDelta /\gamma $ with$ \varOmega /\gamma = 0.2 $ (the first row) and$ \varOmega /\gamma = 2 $ (the second row): (a1), (a2)$ {n_1} = 1 $ ,$ {n_2} = 41 $ ; (b1), (b2)$ {n_1} = 21 $ ,$ {n_2} = 21 $ ; (c1), (c2)$ {n_1} = 41 $ ,$ {n_2} = 1 $ .
图 5 (a1)—(c1)
$ \varDelta = 0 $ 时, 稳态亚超级原子激发概率$ {P_1} $ ,$ {P_2} $ 以及并发纠缠$ C $ 作为$ \varOmega /\gamma $ 和$ {n_1} $ 函数; (a2)—(c2)$ \varOmega /\gamma = 2 $ 时, 稳态亚超级原子激发概率$ {P_1} $ ,$ {P_2} $ 以及并发纠缠$ C $ 作为$ \varDelta /\gamma $ 和$ {n_1} $ 函数; (c1), (c2) 红色截面代表$ C \equiv 0.15 $ 的平面, 其他参数$ n = 42 $ Figure 5. (a1)–(c1) Steady-state excitation probabilities of sub-superatoms
$ {P_1} $ ,$ {P_2} $ and the concurrence$ C $ as a function of$ \varOmega /\gamma $ and$ {n_1} $ with$ \varDelta = 0 $ ; (a2)–(c2) the steady-state excitation probabilities of sub-superatoms$ {P_1} $ ,$ {P_2} $ and the concurrence$ C $ as a function of$ \varDelta /\gamma $ and$ {n_1} $ with$ \varOmega /\gamma = 2 $ ; (c1), (c2) the red cross sections in panel (c1) and (c2) denote$ C \equiv 0.15 $ , other parameter is$ n = 42 $ . -
[1] Martin G 2015 Phys. Rev. A 92 013629
Google Scholar
[2] Zhou M T, Liu J T, Sun P F, An Z Y, Li J, Bao X H, Pan J W 2020 Phys. Rev. A 102 013706
Google Scholar
[3] Pitalúa-García D 2013 Phys. Rev. Lett. 110 210402
Google Scholar
[4] Rao D D B, Klaus M 2014 Phys. Rev. A 89 030301
Google Scholar
[5] Gorniaczyk H, Tresp C, Schmidt J, Fedder H, Hofferberth S 2014 Phys. Rev. Lett. 113 053601
Google Scholar
[6] David P, Georgios M N 2014 Phys. Rev. A 89 013419
Google Scholar
[7] Li D X, Shao X Q 2018 Phys. Rev. A 98 062338
Google Scholar
[8] Mario B, Fernando G, Brandão S L 2018 Phys. Rev. Lett. 121 040504
Google Scholar
[9] Feng D, Hu X Y 2020 Phys. Rev. A 102 042404
Google Scholar
[10] Dong Y, Zhang S Y, Wang Y, Duan L M, Deng D L 2022 Phys. Rev. R 4 023095
Google Scholar
[11] Zhang C H, Peter G, Wolynes, Martin G 2022 Phys. Rev. A 105 033322
Google Scholar
[12] Parmee C D, Cooper N R 2018 Phys. Rev. A 97 053616
Google Scholar
[13] Bhaktavatsala R D D, Klaus M 2014 Phys. Rev. A 90 062319
Google Scholar
[14] Thomas M, Ivana V, Michael J H, Walter H 2016 Phys. Rev. A 94 013809
Google Scholar
[15] Soriente M, Donner T, Chitra R, Zilberberg O 2018 Phys. Rev. Lett. 120 183603
Google Scholar
[16] Stanojevic J, Côté R 2009 Phys. Rev. A 80 033418
Google Scholar
[17] Johannes Z, Peter S, Sebastian H 2015 Phys. Rev. X 5 031015
Google Scholar
[18] Fabian L 2017 New J. Phys. 19 113014
Google Scholar
[19] Zhao P Z, Wu X, Xing T H, Xu G F, Tong D M 2018 Phys. Rev. A 98 032313
Google Scholar
[20] Asaf P, Christoph B, Jan K, Christoph T, Ivan M 2017 Phys. Rev. X 7 041010
Google Scholar
[21] Luo Y H, Zhong H S, Manuel E, Wang X L, Peng L, Mario K, Xiao J, Li L, Liu N L, Lu C Y, Anton Z, Pan J W 2019 Phys. Rev. Lett. 123 070505
Google Scholar
[22] Nicolas G, Grégoire R, Wolfgang T, Hugo Z 2002 Rev. Mod. Phys. 74 145
Google Scholar
[23] Scarani V, Bechmann-Pasquinucci H, Cerf N J, Dušek M, Lütkenhaus N, Peev M 2009 Rev. Mod. Phys. 81 1301
Google Scholar
[24] Damian M, Barry C S 2008 Phys. Rev. A 78 042309
Google Scholar
[25] Zhu A D, Xia Y, Fan Q B, Zhang S 2006 Phys. Rev. A 73 022338
Google Scholar
[26] Li X H, Deng F G, Zhou H Y 2006 Phys. Rev. A 74 054302
Google Scholar
[27] Li T, Long G L 2020 New J Phys. 22 063017
Google Scholar
[28] Robert R, Daniel E, Browne Hans J, Briegel 2003 Phys. Rev. A 68 022312
Google Scholar
[29] James A P, Zhang Y T, Gennady P B, Sabre K 2013 Phys. Rev. E 87 062704
Google Scholar
[30] Li T, Yin Z Q 2016 Sci. Bull. 61 163
Google Scholar
[31] Horodecki R, Horodecki P, Horodecki M, Horodecki K 2009 Rev. Mo. Phys. 81 865
Google Scholar
[32] Deng D L, Li X, Das Sarma S 2017 Phys. Rev. X 7 021021
Google Scholar
[33] Ji Y Q, Liu Y L, Zhou S J, Xiu X M, Dong L, Dong H K, Gao Y J, Yi X X 2019 Phys. Rev. A 99 023808
Google Scholar
[34] Wang T J, Lu Y, Long G L 2012 Phys. Rev. A 86 042337
Google Scholar
[35] Kiesel N, Schmid C, Tóth G, Solano E, Weinfurter H 2007 Phys. Rev. Lett. 98 063604
Google Scholar
[36] Nicolas L 2016 Phys. Rep. 6 008
Google Scholar
[37] Maksym K, Cao J S 2005 Phys. Rev. Lett. 95 180405
Google Scholar
[38] Salcedo L L 2012 Phys. Rev. A 85 022127
Google Scholar
[39] Yan D, Bai W J, Bai J N, Chen L, Han H Y, Wu J H 2022 Photonics 9 242
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 2907
- PDF Downloads: 85
- Cited By: 0
