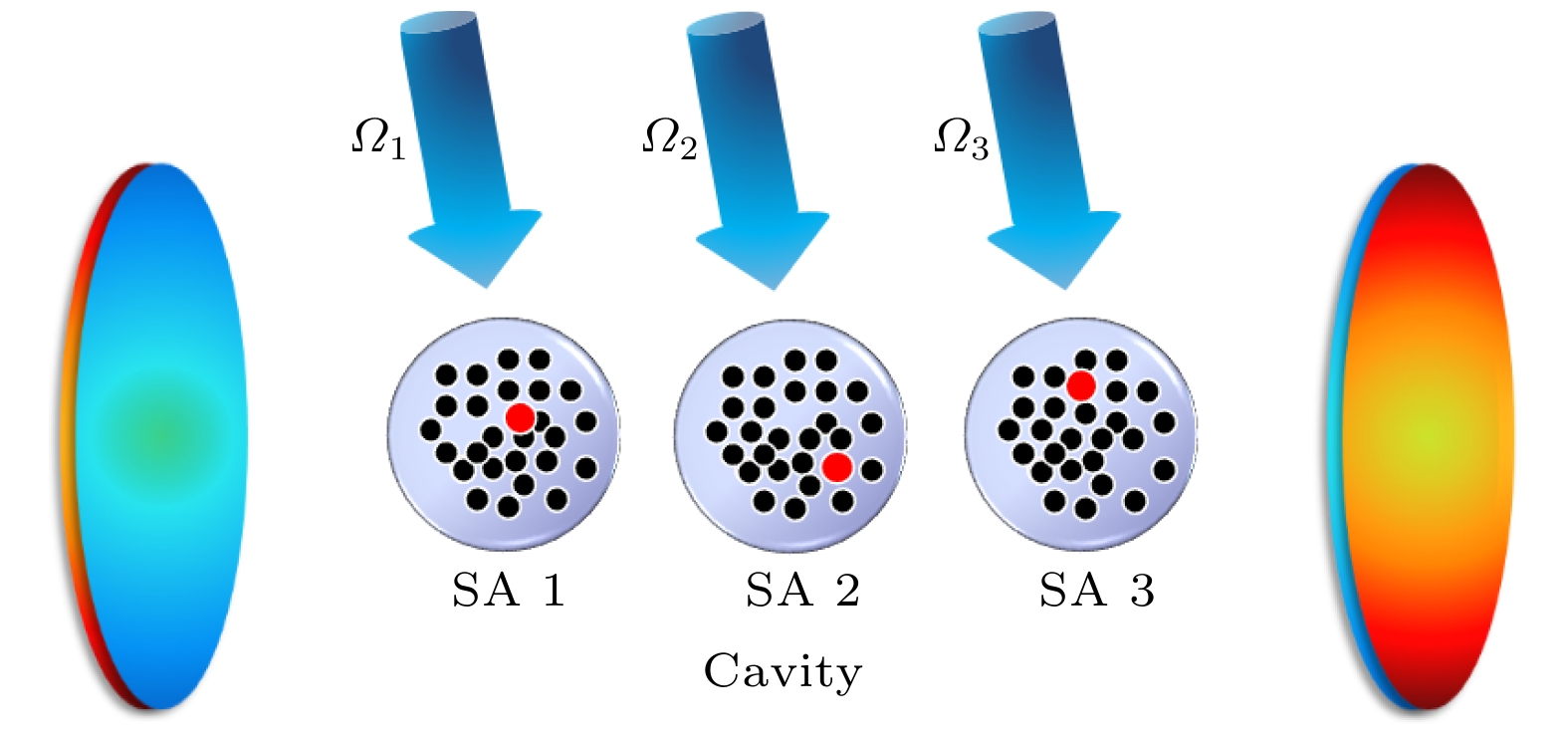
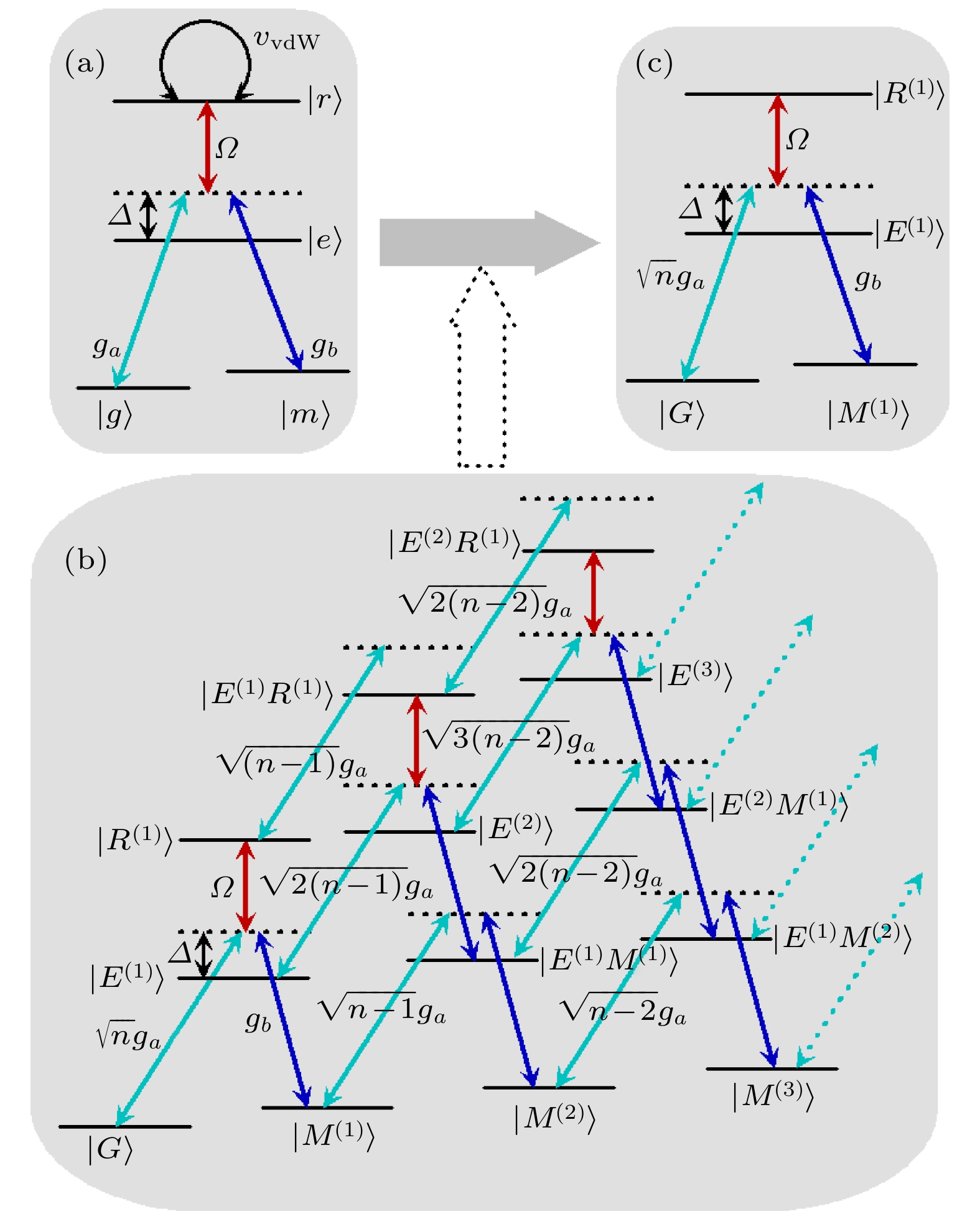
-
量子纠缠是量子信息处理和量子计算的基本资源, 简单而高效地制备纠缠态始终是学者们研究的热点问题之一. 作为量子信息编码理想载体之一的中性里德伯原子, 以其独特的优势在纠缠态制备领域占有一席之地. 本文将四能级倒“Y”型结构的里德伯原子系综放置于里德伯阻塞球内部使之形成超级原子, 在弱腔场近似下将量子信息编码在超级原子的有效能级上, 结合量子Zeno 动力学和绝热捷径的方法, 简单有效地制备了三粒子单重态. 此外, 本方案考虑了退相干因素(包括腔的衰减和超级原子的自发辐射)对单重态保真度的影响. 数值模拟结果表明, 本方案不需要对系统演化时间进行精确的控制就可以得到很高的保真度, 并且单重态的保真度对退相干因素是比较鲁棒的.Quantum entanglement is a basic resource of quantum information processing and quantum computation. The simple and efficient generation of entangled states is always one of the hot research topics. As one of the ideal carriers of quantum information encoding, neutral Rydberg atom occupies a place in the field of generation of entangled state with its unique advantages. For example, Rydberg atom has a large volume and is easily ionized by an external electric field, so it is very sensitive to the change in the external electric field. Therefore, the interaction strength between Rydberg atoms can be changed by altering the external electric field. Rydberg state is a highly excited state, but its radiation attenuation is very small: the radiation lifetime can reach a millisecond level or even longer. The distance between the atomic kernel and the outermost electron is relatively long, and the electric dipole moment is very large. In this paper, the four-level inverted “Y”-type Rydberg atomic system is introduced into the Rydberg blocking ball to form a superatom, and the quantum information is encoded on the effective energy level of the superatom under the condition of weak cavity field. We construct shortcuts to adiabatic passage in a three-superatom system. Combined with quantum Zeno dynamics and shortcuts to adiabatic passage, the three-particle singlet state is simply and effectively generated. In addition, the influence of decoherence factors (including cavity decay and spontaneous emission of superatoms) on the fidelity is considered in this scheme. Numerical simulation results show that the proposed scheme can obtain high fidelity without precisely controlling the evolution time, and the fidelity of singlet state is robust to decoherence factors, since no cavity-photon population is involved in the whole process because of the quantum Zeno dynamics.
-
Keywords:
- superatom /
- singlet state /
- shortcuts to adiabatic passage
[1] Cabello A 2002 Phys. Rev. Lett. 89 100402
Google Scholar
[2] Mermin N D 1980 Phys. Rev. D 22 356
Google Scholar
[3] Cabello A 2003 J. Mod. Opt. 50 1049
Google Scholar
[4] Hsu L Y 2003 Phys. Rev. A 68 022306
Google Scholar
[5] Hillery M, Bužek V 2001 Phys. Rev. A 64 042303
Google Scholar
[6] Jin G S, Li S S, Feng S L, Zheng H Z 2005 Phys. Rev. A 71 034307
Google Scholar
[7] Lin G W, Ye M Y, Chen L B, Du Q H, Lin X M 2007 Phys. Rev. A 76 014308
Google Scholar
[8] Shao X Q, Wang H Fu, Chen L, Zhang S, Zhao Y F, Yeon K H 2010 New J. Phys. 12 023040
Google Scholar
[9] Lu M, Xia Y, Song J, Song H S 2013 J. Phys. B: At. Mol. Opt. Phys. 46 015502
Google Scholar
[10] Shi Z C, Xia Y, Song J, Song H S 2013 Quantum Inf. Process. 12 411
Google Scholar
[11] Jaksch D, Cirac J I, Zoller P, Rolston S L, Côté R, Lukin M D 2000 Phys. Rev. Lett. 85 2208
Google Scholar
[12] Vogt T, Viteau M, Zhao J, Chotia A, Comparat D, Pillet P 2006 Phys. Rev. Lett. 97 083003
Google Scholar
[13] Honer J, Löw R, Weimer H, Pfau T, Büchler H P 2011 Phys. Rev. Lett. 107 093601
Google Scholar
[14] Gaëtan A, Miroshnychenko Y, Wilk T, Chotia A, Viteau M, Comparat D, Pillet P, Browaeys A, Grangier P 2009 Nat. Phys. 5 115
Google Scholar
[15] Urban E, Johnson T A, Henage T, Isenhower L, Yavuz D D, Walker T G, Saffman M 2009 Nat. Phys. 5 110
Google Scholar
[16] Su S L, Liang E J, Zhang S, Wen J J, Sun l l, Jin Z, Zhu A D 2016 Phys. Rev. A 93 012306
Google Scholar
[17] Su S L, Tian Y Z, Shen H Z, Zang H P, Liang E J, Zhang S 2017 Phys. Rev. A 96 042335
Google Scholar
[18] Su S L, Gao Y, Liang E J, Zhang S 2017 Phys. Rev. A 95 022319
Google Scholar
[19] Wu J L, Song J, Su S L 2020 Phys. Lett. A 384 126039
Google Scholar
[20] Wu J L, Su S L, Wang Y, Song J, Xia Y, Jiang Y Y 2020 Opt. Lett. 45 1200
Google Scholar
[21] Wu J L, Wang Y, Han J X, Su S L, Xia Y, Jiang Y Y, Song J 2021 Phys. Rev. A 103 012601
Google Scholar
[22] Shao X Q, Li D X, Ji Y Q, Wu J H, Yi X X 2017 Phys. Rev. A 96 012328
Google Scholar
[23] Møller D, Madsen L B, Møller K 2008 Phys. Rev. Lett. 100 170504
Google Scholar
[24] Saffman M, Mølmer K 2009 Phys. Rev. Lett. 102 240502
Google Scholar
[25] Wu H Z, Li Y, Yang Z B, Zheng S B 2017 Phys. Rev. A 95 013842
Google Scholar
[26] Wilk T, Gaëtan A, Evellin C, Wolters J, Miroshnychenko Y, Grangier P, Browaeys A 2010 Phys. Rev. Lett. 104 010502
Google Scholar
[27] Barredo D, Lienhard V, Scholl P, de Léséleuc S, Boulier T, Browaeys A, Lahaye T 2020 Phys. Rev. Lett. 124 023201
Google Scholar
[28] Li D X, Shao X Q 2018 Phys. Rev. A 98 062338
Google Scholar
[29] Wintermantel T M, Wang Y, Lochead G, Shevate S, Brennen G K, Whitlock S 2020 Phys. Rev. Lett. 124 070503
Google Scholar
[30] Colombe Y, Steinmetz T, Dubois G, Linke F, Hunger D, Reichel J 2007 Nature 450 272
Google Scholar
[31] Pritchard J D, Maxwell D, Gauguet A, Weatherill K J, Jones M P A, Adams C S 2010 Phys. Rev. Lett. 105 193603
Google Scholar
[32] Lukin M D, Fleischhauer M, Cote R, Duan L M, Jaksch D, Cirac J I, Zoller P 2001 Phys. Rev. Lett. 87 037901
Google Scholar
[33] Scully M O, Fry E S, Ooi C H R, Wódkiewicz K 2006 Phys. Rev. Lett. 96 010501
Google Scholar
[34] Yan D, Liu Y M, Bao Q Q, Fu C B, Wu J H 2012 Phys. Rev. A 86 023828
Google Scholar
[35] Yan D, Cui C L, Liu Y M, Song L J, Wu J H 2013 Phys. Rev. A 87 023827
Google Scholar
[36] Liu Y M, Yan D, Tian X D, Cui C L, Wu J H 2014 Phys. Rev. A 89 033839
Google Scholar
[37] Zeiher J, Schauß P, Hild S, Macrì T, Bloch I, Gross C 2015 Phys. Rev. X 5 031015
Google Scholar
[38] Beterov I I, Saffman M, Yakshina E A, Tretyakov D B, Entin V M, Hamzina G N, Ryabtsev I I 2016 J. Phys. B: At. Mol. Opt. Phys. 49 114007
Google Scholar
[39] Paris-Mandoki A, Braun C, Kumlin J, Tresp C, Mirgorodskiy I, Christaller F, Büchler H P, Hofferberth S 2017 Phys. Rev. X 7 041010
Google Scholar
[40] Misra B, Sudarshan E C G 1977 J. Math. Phys. 18 765
[41] Itano W M, Heinzen D J, Bollinger J J, Wineland D J 1990 Phys. Rev. A 41 2295
Google Scholar
[42] Facchi P, Gorini V, Marmo G, Pascazio S, Sudarshan E C G 2000 Phys. Lett. A 275 12
Google Scholar
[43] Facchi P, Pascazio S 2002 Phys. Rev. Lett. 89 080401
Google Scholar
[44] Facchi P, Pascazio S 2008 J. Phys. A: Math. Theor. 41 493001
Google Scholar
[45] Berry M V 2009 J. Phys. A: Math. Theor. 42 365303
Google Scholar
[46] Lu M, Xia Y, Shen L T, Song J, An N B 2014 Phys. Rev. A 89 012326
Google Scholar
[47] Chen X, Ruschhaupt A, Schmidt S, del Campo A, Guéry-Odelin D, Muga J G 2010 Phys. Rev. Lett. 104 063002
Google Scholar
[48] Chen X, Muga J G 2010 Phys. Rev. A 82 053403
Google Scholar
[49] Ji Y Q, Liu Y L, Zhou S J, Xiu X M, Dong L, Dong H K, Gao Y J, Yi X X 2019 Phys. Rev. A 99 023808
Google Scholar
[50] Isenhower L, Urban E, Zhang X L, Gill A T, Henage T, Johnson T A, Walker T G, Saffman M 2010 Phys. Rev. Lett. 104 010503
Google Scholar
[51] Zhang X L, Isenhower L, Gill A T, Walker T G, Saffman M 2010 Phys. Rev. A 82 030306
Google Scholar
[52] Guerlin C, Brion E, Esslinger T, Mølmer K 2010 Phys. Rev. A 82 053832
Google Scholar
[53] Zhang X F, Sun Q, Wen Y C, Liu W M, Eggert S, Ji A C 2013 Phys. Rev. Lett. 110 090402
Google Scholar
-
图 1 (a)里德伯原子的能级结构; (b)里德伯超级原子的能级结构; (c)弱腔场极限下的里德伯超级原子能级结构
Fig. 1. (a) Energy levels configuration for Rydberg atom; (b) energy levels configuration for Rydberg superatom; (c) effective energy levels configuration for the superatom in the weak cavity field limit.
图 2 腔与三个超级原子相互作用示意图
Fig. 2. Schematic illustration of the interaction between the a cavity and three superatoms.
图 3 在
$t_{0}=0.14 t_{\rm{c}}$ 和$T=0.19 t_{\rm{c}}$ 时的激光脉冲$\varOmega_{1}'$ 和$\varOmega_{3}'$ Fig. 3. Laser pulse
$\varOmega_{1}'$ and$\varOmega_{3}'$ when$t_{0}=0.14 t_{\rm{c}}$ and$T= $ $ 0.19 t_{\rm{c}}$ .
图 4 利用绝热近似方法和绝热捷径方法制备三粒子单重态所需时间对比
Fig. 4. Comparison of the interaction time required between shortcuts to the adiabaticity method and the adiabatic approximation method.
图 5 (a) 三粒子单重态的保真度随相互作用时间
$g_{0}t_{\rm c}$ 和原子自发辐射$\gamma/g_{0}$ 的变化; (b) 三粒子单重态的保真度随腔衰减$\kappa/g_{0}$ 和原子自发辐射$\gamma/g_{0}$ 的变化Fig. 5. (a) Fidelity of the singlet state versus the interaction time
$g_{0}t_{\rm c}$ and the atomic spontaneous emission$\gamma/g_{0}$ ; (b) fidelity of the singlet state versus the cavity decay$\kappa/g_{0}$ and the atomic spontaneous emission$\gamma/g_{0}$ -
[1] Cabello A 2002 Phys. Rev. Lett. 89 100402
Google Scholar
[2] Mermin N D 1980 Phys. Rev. D 22 356
Google Scholar
[3] Cabello A 2003 J. Mod. Opt. 50 1049
Google Scholar
[4] Hsu L Y 2003 Phys. Rev. A 68 022306
Google Scholar
[5] Hillery M, Bužek V 2001 Phys. Rev. A 64 042303
Google Scholar
[6] Jin G S, Li S S, Feng S L, Zheng H Z 2005 Phys. Rev. A 71 034307
Google Scholar
[7] Lin G W, Ye M Y, Chen L B, Du Q H, Lin X M 2007 Phys. Rev. A 76 014308
Google Scholar
[8] Shao X Q, Wang H Fu, Chen L, Zhang S, Zhao Y F, Yeon K H 2010 New J. Phys. 12 023040
Google Scholar
[9] Lu M, Xia Y, Song J, Song H S 2013 J. Phys. B: At. Mol. Opt. Phys. 46 015502
Google Scholar
[10] Shi Z C, Xia Y, Song J, Song H S 2013 Quantum Inf. Process. 12 411
Google Scholar
[11] Jaksch D, Cirac J I, Zoller P, Rolston S L, Côté R, Lukin M D 2000 Phys. Rev. Lett. 85 2208
Google Scholar
[12] Vogt T, Viteau M, Zhao J, Chotia A, Comparat D, Pillet P 2006 Phys. Rev. Lett. 97 083003
Google Scholar
[13] Honer J, Löw R, Weimer H, Pfau T, Büchler H P 2011 Phys. Rev. Lett. 107 093601
Google Scholar
[14] Gaëtan A, Miroshnychenko Y, Wilk T, Chotia A, Viteau M, Comparat D, Pillet P, Browaeys A, Grangier P 2009 Nat. Phys. 5 115
Google Scholar
[15] Urban E, Johnson T A, Henage T, Isenhower L, Yavuz D D, Walker T G, Saffman M 2009 Nat. Phys. 5 110
Google Scholar
[16] Su S L, Liang E J, Zhang S, Wen J J, Sun l l, Jin Z, Zhu A D 2016 Phys. Rev. A 93 012306
Google Scholar
[17] Su S L, Tian Y Z, Shen H Z, Zang H P, Liang E J, Zhang S 2017 Phys. Rev. A 96 042335
Google Scholar
[18] Su S L, Gao Y, Liang E J, Zhang S 2017 Phys. Rev. A 95 022319
Google Scholar
[19] Wu J L, Song J, Su S L 2020 Phys. Lett. A 384 126039
Google Scholar
[20] Wu J L, Su S L, Wang Y, Song J, Xia Y, Jiang Y Y 2020 Opt. Lett. 45 1200
Google Scholar
[21] Wu J L, Wang Y, Han J X, Su S L, Xia Y, Jiang Y Y, Song J 2021 Phys. Rev. A 103 012601
Google Scholar
[22] Shao X Q, Li D X, Ji Y Q, Wu J H, Yi X X 2017 Phys. Rev. A 96 012328
Google Scholar
[23] Møller D, Madsen L B, Møller K 2008 Phys. Rev. Lett. 100 170504
Google Scholar
[24] Saffman M, Mølmer K 2009 Phys. Rev. Lett. 102 240502
Google Scholar
[25] Wu H Z, Li Y, Yang Z B, Zheng S B 2017 Phys. Rev. A 95 013842
Google Scholar
[26] Wilk T, Gaëtan A, Evellin C, Wolters J, Miroshnychenko Y, Grangier P, Browaeys A 2010 Phys. Rev. Lett. 104 010502
Google Scholar
[27] Barredo D, Lienhard V, Scholl P, de Léséleuc S, Boulier T, Browaeys A, Lahaye T 2020 Phys. Rev. Lett. 124 023201
Google Scholar
[28] Li D X, Shao X Q 2018 Phys. Rev. A 98 062338
Google Scholar
[29] Wintermantel T M, Wang Y, Lochead G, Shevate S, Brennen G K, Whitlock S 2020 Phys. Rev. Lett. 124 070503
Google Scholar
[30] Colombe Y, Steinmetz T, Dubois G, Linke F, Hunger D, Reichel J 2007 Nature 450 272
Google Scholar
[31] Pritchard J D, Maxwell D, Gauguet A, Weatherill K J, Jones M P A, Adams C S 2010 Phys. Rev. Lett. 105 193603
Google Scholar
[32] Lukin M D, Fleischhauer M, Cote R, Duan L M, Jaksch D, Cirac J I, Zoller P 2001 Phys. Rev. Lett. 87 037901
Google Scholar
[33] Scully M O, Fry E S, Ooi C H R, Wódkiewicz K 2006 Phys. Rev. Lett. 96 010501
Google Scholar
[34] Yan D, Liu Y M, Bao Q Q, Fu C B, Wu J H 2012 Phys. Rev. A 86 023828
Google Scholar
[35] Yan D, Cui C L, Liu Y M, Song L J, Wu J H 2013 Phys. Rev. A 87 023827
Google Scholar
[36] Liu Y M, Yan D, Tian X D, Cui C L, Wu J H 2014 Phys. Rev. A 89 033839
Google Scholar
[37] Zeiher J, Schauß P, Hild S, Macrì T, Bloch I, Gross C 2015 Phys. Rev. X 5 031015
Google Scholar
[38] Beterov I I, Saffman M, Yakshina E A, Tretyakov D B, Entin V M, Hamzina G N, Ryabtsev I I 2016 J. Phys. B: At. Mol. Opt. Phys. 49 114007
Google Scholar
[39] Paris-Mandoki A, Braun C, Kumlin J, Tresp C, Mirgorodskiy I, Christaller F, Büchler H P, Hofferberth S 2017 Phys. Rev. X 7 041010
Google Scholar
[40] Misra B, Sudarshan E C G 1977 J. Math. Phys. 18 765
[41] Itano W M, Heinzen D J, Bollinger J J, Wineland D J 1990 Phys. Rev. A 41 2295
Google Scholar
[42] Facchi P, Gorini V, Marmo G, Pascazio S, Sudarshan E C G 2000 Phys. Lett. A 275 12
Google Scholar
[43] Facchi P, Pascazio S 2002 Phys. Rev. Lett. 89 080401
Google Scholar
[44] Facchi P, Pascazio S 2008 J. Phys. A: Math. Theor. 41 493001
Google Scholar
[45] Berry M V 2009 J. Phys. A: Math. Theor. 42 365303
Google Scholar
[46] Lu M, Xia Y, Shen L T, Song J, An N B 2014 Phys. Rev. A 89 012326
Google Scholar
[47] Chen X, Ruschhaupt A, Schmidt S, del Campo A, Guéry-Odelin D, Muga J G 2010 Phys. Rev. Lett. 104 063002
Google Scholar
[48] Chen X, Muga J G 2010 Phys. Rev. A 82 053403
Google Scholar
[49] Ji Y Q, Liu Y L, Zhou S J, Xiu X M, Dong L, Dong H K, Gao Y J, Yi X X 2019 Phys. Rev. A 99 023808
Google Scholar
[50] Isenhower L, Urban E, Zhang X L, Gill A T, Henage T, Johnson T A, Walker T G, Saffman M 2010 Phys. Rev. Lett. 104 010503
Google Scholar
[51] Zhang X L, Isenhower L, Gill A T, Walker T G, Saffman M 2010 Phys. Rev. A 82 030306
Google Scholar
[52] Guerlin C, Brion E, Esslinger T, Mølmer K 2010 Phys. Rev. A 82 053832
Google Scholar
[53] Zhang X F, Sun Q, Wen Y C, Liu W M, Eggert S, Ji A C 2013 Phys. Rev. Lett. 110 090402
Google Scholar
下载:
计量
- 文章访问数: 4641
- PDF下载量: 81
- 被引次数: 0
