-
电场与里德伯态能级互相作用产生Stark效应可以通过EIT光谱的频移量进行量子探测, 利用频移量与电场之间的函数关系, 能够实现电场的测量. 但是当探测光与耦合光偏振方向失配时会导致频移量的测量结果出现误差, 进而影响电场的准确测量. 本文首先求解密度矩阵方程进而推导EIT-Stark数学模型, 分析探测光和耦合光偏振方向对模型的影响. 其次, 本文采用内置极板的方法避免了由于碱金属原子附着在原子蒸气室表面对加载电场所造成的屏蔽作用. 最后, 通过调控激光偏振方向, 验证了偏振失配对EIT光谱以及电场测量结果的影响. 实验数据显示, 探测光和耦合光偏振方向互为平行时, 为激光最匹配的偏振方向, EIT光谱峰值最大, 电场测量最大相对误差为1.67%. 探测光和耦合光偏振方向夹角为45°时, 激光偏振失配程度最严重, EIT光谱峰值最小, 电场测量最大相对误差为10.24%.The interaction between an electric field and the energy levels of Rydberg states results in the Stark effect, which can be used for quantum detection by measuring the frequency shift in electromagnetically induced transparency (EIT) spectra. By using the functional relationship between the frequency shift and the electric field, it is possible to measure the electric field in question. However, the mismatch between the probe laser and the polarization direction of the coupled laser leads to errors in the measurement of the frequency shift, affecting the accurate measurement of the electric field. In this work, the Schrödinger equation is solved by perturbation method to derive the functional relationship between the energy offset and the electric field strength. Then, the functional relationship between the energy offset and the electric field strength is brought into the solution of the density matrix equation, and the influences of the polarization direction of the detected light and coupled light on the EIT-Stark mathematical model are analyzed. Then an internal electrode method is used to prevent shielding effects caused by alkali metal atoms adhering to the surface of the atomic vapor cell, thereby enabling the application of the electric field. The calibration of the Rydberg state polarisation rate is achieved by using a standard source and measuring the frequency shift of the EIT spectrum. Finally, the effects of polarisation mismatch on the measurement results of EIT spectrum and the electric field are verified by modulating the laser polarization direction. The experimental data show that when the polarization directions of the probe laser and coupled laser are parallel to each other, it is the most matched polarization direction for the lasers, the peak value of the EIT spectrum is the largest, and the maximum relative error of the electric field measurement is 1.67%. When the angle between the polarisation directions of the probe light and the coupled light laser is 45°, the laser polarisation mismatch is the most severe, the EIT spectral peak is the lowest and the maximum relative error of the electric field measurement is 10.24%.
-
Keywords:
- electric field measurement /
- Rydberg atom /
- electromagnetically induced transparency /
- direction of laser polarisation
-
图 3 饱和光谱法稳频结构图
Fig. 3. Structural diagram of frequency stabilisation by saturation spectroscopy.
图 4 饱和光谱法锁频原理图 (a) 饱和光谱图; (b) 精细能级结构; (c) 饱和光谱及其鉴频曲线
Fig. 4. Schematic diagram of frequency locking by saturation spectroscopy: (a) Saturation spectrum; (b) fine structure levels; (c) saturation spectrum and its frequency discrimination curve.
图 9 EIT光谱峰值随双光子偏振夹角增加变化曲线
Fig. 9. Variation curve of EIT spectral peak with increasing two-photon polarisation pinch angle.
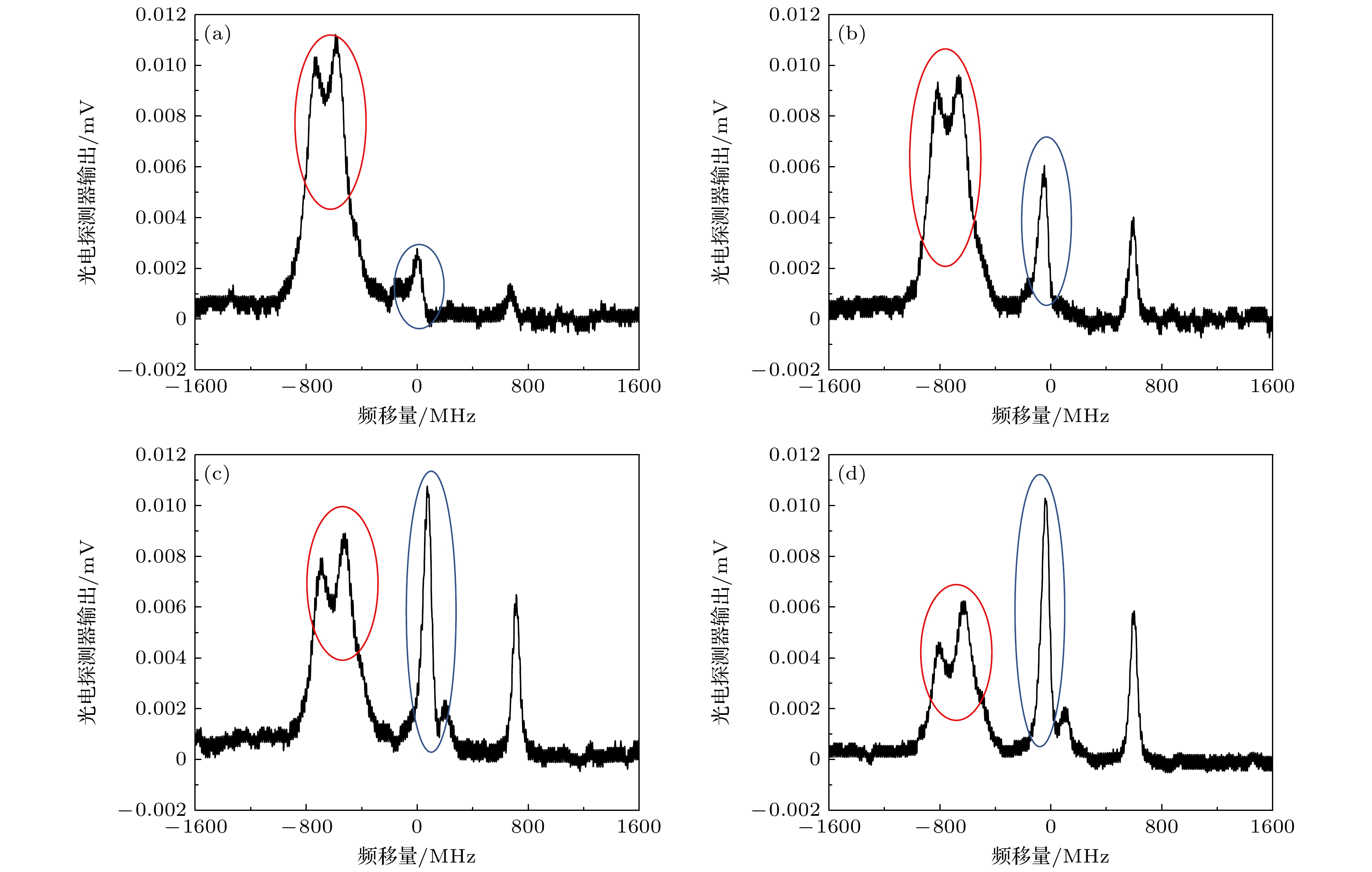
图 11 激光偏振方向对EIT光谱的影响 (a)探测光和耦合光偏振方向平行; (b) 探测光和耦合光偏振方向夹角20°; (c) 探测光和耦合光偏振方向夹角45°; (d) 探测光和耦合光偏振方向垂直
Fig. 11. Effect of laser polarisation direction on EIT spectra: (a) Polarization directions of the probe light and coupling light are parallel; (b) the polarization directions of the probe light and coupling light form an angle of 20°; (c) the polarization directions of the probe light and coupling light form an angle of 45°; (d) the polarization directions of the probe light and coupling light are perpendicular.
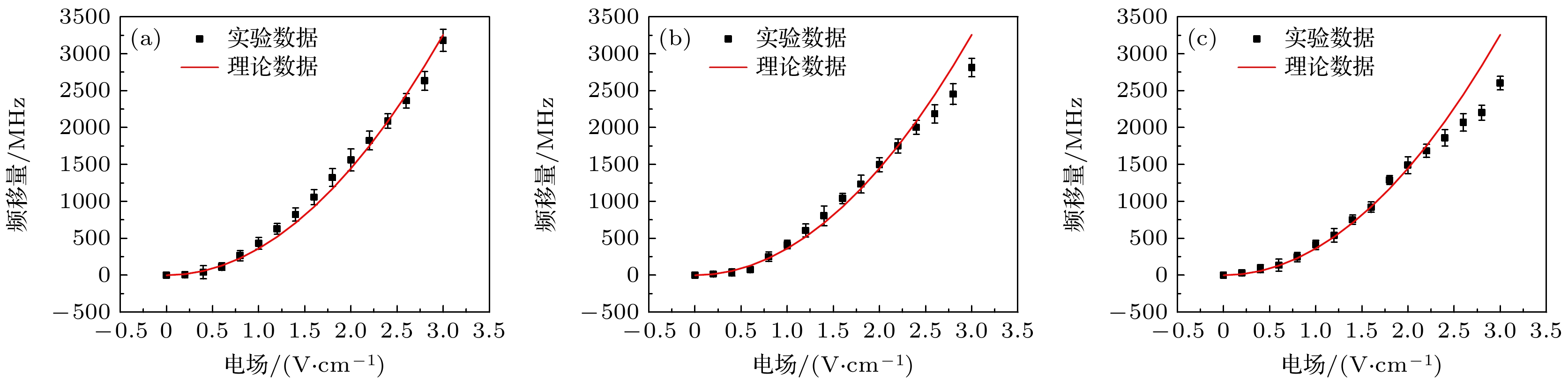
图 13 测量结果 (a)探测光和耦合光偏振方向平行; (b)探测光和耦合光偏振方向夹角22.5°; (c)探测光和耦合光偏振方向夹角45°
Fig. 13. Measurement results: (a) Parallelism between the direction of polarisation of the probe and coupled laser; (b) 22.5° angle between the direction of polarisation of the probe and coupled laser; (c) 45° angle between the direction of polarisation of the d probe and coupled laser.
-
[1] Holloway C L, Prajapati N, Simons M T, Artusio-Glimpse A 2022 IEEE Microw. Mag. 23 44
[2] 张学超, 乔佳慧, 刘瑶, 苏楠, 刘智慧, 蔡婷, 何军, 赵延霆, 王军民 2024 73 070201
Zhang X C, Qiao J H, Liu Y, Su N, Liu Z H, Cai T, He J, Zhao Y T, Wang J M 2024 Acta Phys. Sin. 73 073201
[3] 夏刚, 张亚鹏, 汤婧雯, 李春燕, 吴春旺, 张杰, 周艳丽 2024 73 104203
Google Scholar
Xia G, Zhan Y P, Tang J W, Li C Y, Wu C W, Zhang J, Zhou Y L 2024 Acta Phys. Sin. 73 104203
Google Scholar
[4] Hao L, Xue Y, Fan J, Bai J, Jiao Y, Zhao J 2020 Chin. Phys. B 29 033201
Google Scholar
[5] 张淳刚, 李伟, 张好, 景明勇, 张临杰 2021 光子学报 50 0602001
Zhang C G, Li W, Zhang H, Jing M Y, Zhang L J 2021 Acta Photon. Sin. 50 0602001
[6] 李伟, 张淳刚, 张好, 景明勇, 张临杰 2021 激光与光电子学进展 58 1702002
Li W, Zhang C G, Zhang H, Jing M Y, Zhang L J 2021 Laser Optoelectron. Prog. 58 1702002
[7] Hu J L, Li H Q, Song R, Bai J X, Jiao Y C, Zhao J M, Jia S T 2022 Appl. Phys. Lett. 121 014002
Google Scholar
[8] Gordon J A, Simons M T, Haddab A H, Holloway C L 2019 AIP Adv. 9 045030
Google Scholar
[9] Amy K R, Nikunjkumar P, Senic D 2021 Appl. Phys. Lett. 118 114001
Google Scholar
[10] 阮伟民, 张映昀, 冯志刚, 周亚东, 宋振飞, 屈继峰 2024 计量学报 45 97
Google Scholar
Ruan W M, Zhang Y Y, Feng Z G, Zhou Y D, Song Z F, Qu J F 2024 Acta Metrol. Sin. 45 97
Google Scholar
[11] 张映昀, 阮伟民, 冯志刚, 屈继峰, 宋振飞 2023 计量学报 44 1438
Google Scholar
Zhang Y Y, Ruan W M, Feng Z G, Qu J F, Song Z F 2023 Acta Metrologica Sinca 44 1438
Google Scholar
[12] 李可, 田建飞, 张好, 景明勇, 张临杰 2023 光子学报 52 0902001
Google Scholar
Li K, Tian J F, Zhang H, Jing M Y, Zhang L J 2023 Acta Photon. Sin. 52 0902001
Google Scholar
[13] 刘修彬, 贾凤东, 周飞, 俞永宏, 张剑, 谢锋, 钟志萍 2023 宇航计测技术 43 5
Google Scholar
Liu X, Jia F, Zhou F, Yu Y, Zhang J, Xie F, Zhong Z 2023 J. Astron. Metrol. Measurem. 43 5
Google Scholar
[14] Cai M H, Xu Z S, You S H, Liu H P 2022 Photonics 9 250
Google Scholar
[15] 蔡德成, 胡星, 吴海洋, 吕健双 2023 电力大数据 26 90
Cai D C, Hu X, Wu H Y, Lv J S 2023 Power Syst. Big Data 26 90
[16] 张缘圆, 辛明勇, 冯起辉, 祝健杨 2023 电力大数据 26 69
Zhang Y Y, Xin M Y, Feng Q H, Zhu J Y 2023 Power Syst. Big Data 26 69
[17] Liu W, Zhang L, Wang T 2023 Chin. Phys. B 32 053203
Google Scholar
[18] Zhao S S, Gao W, Cheng H, You L, Liu H P 2018 Phys. Rev. Lett. 120 063203
Google Scholar
[19] 韩玉龙, 刘邦, 张侃, 孙金芳, 孙辉, 丁冬生 2024 73 113201
Google Scholar
Han Y L, Liu B, Zhang K, Sun J F, Sun H, Ding D S 2024 Acta Phys. Sin. 73 113201
Google Scholar
[20] 阎晟, 肖冬萍, 石筑鑫, 张淮清 刘卫华 2024 电工技术学报 39 2953
Yan S, Xiao D P, Shi Z X, Zhang H Q, Liu W H 2024 Transactions of China Electrotechnical Society 39 2953
[21] 王延正, 武博, 付运起, 安强 2024 激光与光电子学进展 OL
Wang Y Z, Wu B, Fu Y Q, An Q 2024 Laser Optoelectron. Prog. OL
[22] Noah S, Andrew P R, Alexandra B A, Nikunjkumar P, Samuel B, Dangka S, Matthew T S, Christopher L H 2024 Phys. Rev. A 109 L021702
[23] Sedlacek J A, Schwettmann A, Kubler H, Shaffer J P 2013 Phys. Rev. Lett. 111 063001
[24] Bao S X, Zhang H, Zhou J, Zhang L J, Zhao J M, Xiao L T, Jia S T 2016 Phys. Rev. A 94 043822
Google Scholar
下载:
计量
- 文章访问数: 416
- PDF下载量: 18
- 被引次数: 0
