-
本文在典型的里德伯电磁感应透明系统中研究弱探测场在相互作用原子系统中的传播特性, 重点关注基于偶极阻塞效应的探测场相位的合作光学非线性行为. 通过与探测场透射率和光子关联作对比, 发现相位的光学响应具有新特性: 共振和Autler-Townes劈裂条件下相位对入射场强和初始光子关联不敏感, 而在两者之间的频率范围内相位响应具有非线性特征, 尤其在经典光频率处最显著. 此外, 提高主量子数和原子密度都会促进相位的非线性效应. 综上, 与探测场透射率和光子关联一样, 相位可以作为合作光学非线性的另一个标识来刻画非线性现象, 对里德伯电磁感应透明研究是一个有力的补充.Transmission properties of a weak probe field traveling through a sample of interacting cold 87Rb atoms driven into the three-level ladder configuration, which is a typical Rydberg electromagnetically induced transparency (EIT) system, are investigated. Rydberg atoms are considered to be a perfect platform in the research fields of quantum optics and quantum information processing due to some exaggerated properties of Rydberg atoms with high principal quantum number, especially, the dipole-dipole interaction between Rydberg atoms leads to the so-called dipole blockade effect accommodating at most one Rydberg excitation within a mesoscopic volume. The dipole blockade effect may be mapped onto the spectrum of EIT, and the EIT exhibits the cooperative optical nonlinearity which is usually characterized by two indicators, i.e., the probe intensity and the photonic correlation. The cooperative optical nonlinearity is also found here in the phase of transmission spectrum, and the phase can be regarded as the third indicator of nonlinearity in Rydberg EIT. However, there are tremendous differences between the phase and probe transmission (photonic correlation) though they both originate from the conditional polarization. Specifically, the phase is not sensitive to neither the incident probe intensity nor the initial photonic correlation at the resonant probe frequency under the condition of the Autler-Townes (AT) splitting where two other indicators exhibit significant cooperative nonlinearity. The nonlinearity in phase spectrum occurs only in the regime between the resonant probe frequency and the AT splitting and especially is remarkable at the frequency where the probe field is classical. Finally, influence of the principal quantum number and the atomic density on the transmitted phase are examined. In the nonlinear regime, the absolute value of the phase becomes smaller and smaller as the principal quantum number and the atomic density are raised. This indicates that the nonlinearity is strengthened by increasing them. The probe phase provides an attractive supplement to study in depth the cooperative optical nonlinearity in Rydberg EIT and offers us the considerable flexibility to manipulate the propagation and evolution of a quantum light field.
-
Keywords:
- electromagnetically induced transparency /
- dipole-dipole interaction /
- Rydberg atom /
- superatom
[1] Harris S E, Field J E, Imamoglu A 1990 Phys. Rev. Lett. 64 1107
Google Scholar
[2] Harris S E 1997 Physics Today 50 36
[3] Fleichhauer M, Imamoglu A, Marangos J P 2005 Rev. Mod. Phys. 77 633
Google Scholar
[4] Kasapi A, Jain M, Yin G Y, Harris S E 1995 Phys. Rev. Lett. 74 2447
Google Scholar
[5] Hau L V, Harris S E, Dutton Z, Behroozi C H 1999 Nature 397 594
Google Scholar
[6] Kash M M, Sautenkov V A, Zibrov A S, Hollberg L, Welch G R, Lukin M D, Rostovtsev Y, Fry E S, Scully M O 1999 Phys. Rev. Lett. 82 5229
Google Scholar
[7] Lukin M D 2003 Rev. Mod. Phys. 75 457
Google Scholar
[8] Fleichhauer M, Lukin M D 2000 Phys. Rev. Lett. 84 5094
Google Scholar
[9] Simon C, Afzelius M, Appel J, de la Giroday A B, Dewhurst S J, Gisin N, Hu C Y, Jelezko F, Kröll S, Müller J H, Nunn J, Polzik E S, Rarity J G, de Riedmatten H, Rosenfeld W, Shields A J, Sköld N, Stevenson R M, Thew R, Walmsley I A, Weber M C, Weinfurter H, Wrachtrup J, Young R J 2010 Eur. Phys. J. D. 58 1
Google Scholar
[10] Eisaman M D, Andre A, Massou M, Fleichhauer M, Zibrov A S, Lukin M D 2005 Nature 438 837
Google Scholar
[11] Chanelière T, Matsukevich D N, Jenkins S D, Lan S Y, Kennedy T A B, Kuzmich A 2005 Nature 438 833
Google Scholar
[12] De Araujo L E E 2010 Opt. Lett. 35 977
Google Scholar
[13] Artoni M, La Rocca G C 2006 Phys. Rev. Lett. 96 073905
Google Scholar
[14] He Q Y, Xue Y, Artoni M, La Rocca G C, Xu J H, Gao J Y 2006 Phys. Rev. B 73 195124
Google Scholar
[15] Schmidt H, Ram R J 2000 App. Phys. Lett. 76 3173
Google Scholar
[16] Wu J H, La Rocca G C, Artoni M 2008 Phys. Rev. B 77 113106
Google Scholar
[17] Friedler I, Petrosyan D, Fleischhauer M, Kurizki G 2005 Phys. Rev. A 72 043803
Google Scholar
[18] Weatherill K J, Pritchard J D, Abel R P, Bason M G, Mohapatra A K, Adams C S 2008 J. Phys. B: At. Mol. Opt. Phys. 41 201002
Google Scholar
[19] Walker T G 2012 Nature 488 39
Google Scholar
[20] Müller M M, Kölle A, Löw R, Pfau T, Calarco T, Montangero S 2013 Phys. Rev. A 87 053412
Google Scholar
[21] Peyronel T, Firstenberg O, Liang Q Y, Hofferberth S, Gorshkov A V, Pohl T, Lukin M D, Vuletic V 2012 Nature 488 57
Google Scholar
[22] Gorniaczyk H, Tresp C, Schmidt J, Fedder H, Hofferberth S 2014 Phys. Rev. Lett. 113 053601
Google Scholar
[23] Chen W, Beck K M, Bücker R, Gullans M, Lukin M D, Tanji-Suzuki H, Vuletić V 2013 Science 341 768
Google Scholar
[24] Baur S, Tiarks D, Rempe G, Dürr S 2014 Phys. Rev. Lett. 112 073901
Google Scholar
[25] Paredes-Barato D, Adams C S 2014 Phys. Rev. Lett. 112 040501
Google Scholar
[26] Pritchard J D, Maxwell D, Gauguet A, Weatherill K J, Jones M P A, Adams C S 2010 Phys. Rev. Lett. 105 193603
Google Scholar
[27] Sevinçli S, Henkel N, Ates C, Pohl T 2011 Phys. Rev. Lett. 107 153001
Google Scholar
[28] Petrosyan D, Otterbach J, Fleischhauer M 2011 Phys. Rev. Lett. 107 213601
Google Scholar
[29] Yan D, Liu Y M, Bao Q Q, Fu C B, Wu J H 2012 Phys. Rev. A 86 023828
Google Scholar
[30] Yan D, Cui C L, Liu Y M, Song L J, Wu J H 2013 Phys. Rev. A 87 023827
Google Scholar
[31] Liu Y M, Yan D, Tian X D, Cui C L, Wu J H 2014 Phys. Rev. A 89 033839
Google Scholar
[32] Liu Y M, Tian X D, Yan D, Zhang Y, Cui C L, Wu J H 2015 Phys. Rev. A 91 043802
Google Scholar
[33] Liu Y M, Tian X D, Wang X, Yan D, Wu J H 2016 Opt. Lett. 408 41
[34] Singer K, Stanojevic J, Weidemuller M, Cote R 2005 J. Phys. B: At. Mol. Opt. Phys. 38 S295
Google Scholar
-
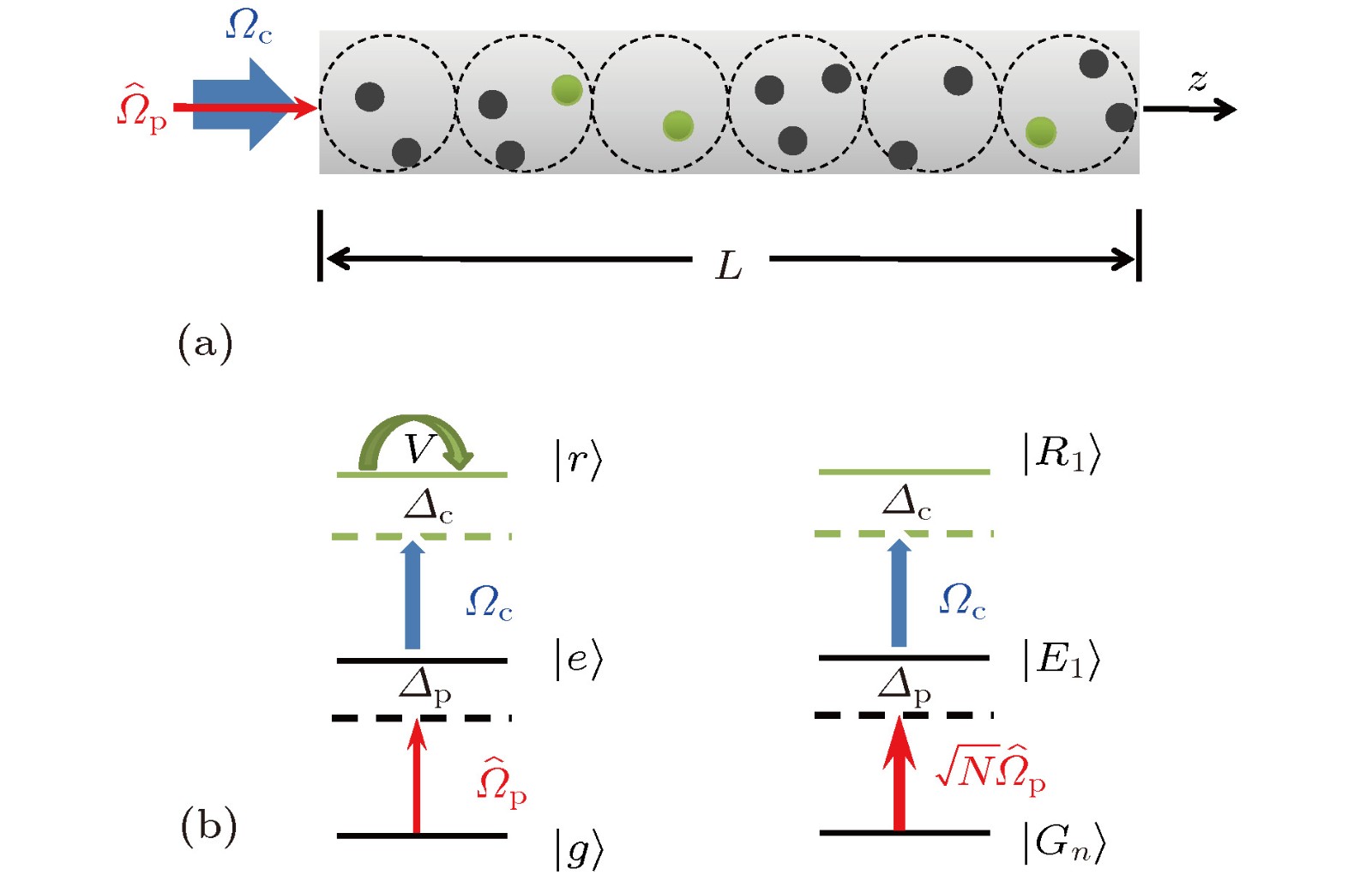
图 1 (a)量子探测场
$\scriptstyle{\hat \varOmega _{\rm{p}}}$ 在控制场${\varOmega _{\rm{c}}}$ 相干作用下的一维冷原子系综中传播, 原子系综可以看作是由独立的超级原子构成的; (b)左侧为具有vdW 相互作用的三能级原子结构图; 右侧为等价的无相互作用超级原子能级结构图Fig. 1. (a) Under the control of a classical field
$ {\varOmega _{\rm{c}}}$ , a quantum probe field$\scriptstyle{\hat \varOmega _{\rm{p}}}$ propagates in a one-dimensional cold atomic ensemble of non-interacting superatoms. (b) Left, level structure of the three-level interacting cold atoms described by a vdW potential; right, an equivalent energy level structure of a non-interacting superatom.
图 2 (a)探测场透射率
${I_{\rm{p}}}(L)/{I_{\rm{p}}}(0)$ , (b)二阶关联函数$g_{\rm{p}}^{(2)}(L)/g_{\rm{p}}^{{\rm{(2)}}}(0)$ , (c)探测场相位${\phi _{\rm{p}}}(L)/{\text{π}}$ 作为探测失谐${\varDelta _{\rm{p}}}/(2{\text{π}})$ 的函数. 黑色实线, 蓝色折线以及红色点线分别对应入射探测场拉比频率${\varOmega _{\rm{p}}}\left( 0 \right)/(2{\text{π}}) = 0.01$ , 0.3 MHz和0.6 MHz的情况. 单光子失谐${\varDelta _{\rm{c}}} = 0$ , 控制场拉比频率${\varOmega _{\rm{c}}}/(2{\text{π}}) = 2.5\;{\rm{MHz}}$ , 其他参数见正文描述Fig. 2. (a) The transmitted probe intensity
${I_{\rm{p}}}(L)/{I_{\rm{p}}}(0)$ , (b) the second-order correlation function$g_{\rm{p}}^{(2)}(L)/g_{\rm{p}}^{{\rm{(2)}}}(0)$ , (c) probe phase${\phi _{\rm{p}}}(L)/{\text{π}}$ as a function of the probe detuning${\varDelta _{\rm{p}}}/(2{\text{π}})$ . The black solid, blue dashed and red dotted curves are corresponding to incident probe Rabi frequencies${\varOmega _{\rm{p}}}\left( 0 \right)/(2{\text{π}}) = 0.01$ ,$0.3\;{\rm{MHz}}$ and$0.6\;{\rm{MHz}}$ , respectively. The single-photon detuning${\varDelta _{\rm{c}}} = 0$ and the Rabi frequency of control field${\varOmega _{\rm{c}}}/(2{\text{π}}) = 2.5\;{\rm{MHz}}$ . Other parameters are described in the text.
图 3 (a)探测场透射率
${I_{\rm{p}}}(L)/{I_{\rm{p}}}(0)$ , (b)二阶关联函数$g_{\rm{p}}^{(2)}(L)/g_{\rm{p}}^{{\rm{(2)}}}(0)$ , (c)探测场相位${\phi _{\rm{p}}}(L)/{\text{π}}$ 作为探测失谐${\varDelta _{\rm{p}}}/(2{\text{π}})$ 和入射探测场拉比频率${\varOmega _{\rm{p}}}\left( 0 \right)/(2{\text{π}})$ 的函数. 其他参数同图2Fig. 3. (a) The transmitted probe intensity
${I_{\rm{p}}}(L)/{I_{\rm{p}}}(0)$ , (b) the second-order correlation function$g_{\rm{p}}^{(2)}(L)/g_{\rm{p}}^{{\rm{(2)}}}(0)$ , (c) the probe phase${\phi _{\rm{p}}}(L)/{\text{π}}$ as a function of the probe detuning${\varDelta _{\rm{p}}}/(2{\text{π}})$ and theRabi frequency of the incident probe field${\varOmega _{\rm{p}}}\left( 0 \right)/(2{\text{π}})$ . Other parameters are the same as in Fig. 2.
图 4 (a)探测场透射率
${I_{\rm{p}}}(L)/{I_{\rm{p}}}(0)$ , (b)二阶关联函数$g_{\rm{p}}^{(2)}(L)/g_{\rm{p}}^{{\rm{(2)}}}(0)$ , (c)探测场相位${\phi _{\rm{p}}}(L)/{\text{π}}$ 作为探测失谐${\varDelta _{\rm{p}}}/(2{\text{π}})$ 和初始二阶关联函数$g_{\rm{p}}^{\left( {\rm{2}} \right)}\left( 0 \right)$ 的函数. 入射探测场拉比频率${\varOmega _{\rm{p}}}\left( 0 \right)/(2{\text{π}}) = 0.3\;{\rm{MHz}}$ , 其他参数同图2Fig. 4. (a) The transmitted probe intensity
${I_{\rm{p}}}(L)/{I_{\rm{p}}}(0)$ , (b) the second-order correlation function$g_{\rm{p}}^{{\rm{(2)}}}(L)/g_{\rm{p}}^{{\rm{(2)}}}(0)$ , (c) probe phase$ {\phi _{\rm{p}}}(L)/{\text{π}} $ as a function of the probe detuning${\varDelta _{\rm{p}}}/(2{\text{π}})$ and the initial second-order correlation function$g_{\rm{p}}^{\left( 2 \right)}\left( 0 \right)$ . The Rabi frequency of the incident probe field${\varOmega _{\rm{p}}}\left( 0 \right)/(2{\text{π}}) = 0.3\;{\rm{MHz}}$ and other parameters are the same as in Fig. 2.
图 5 探测场相位
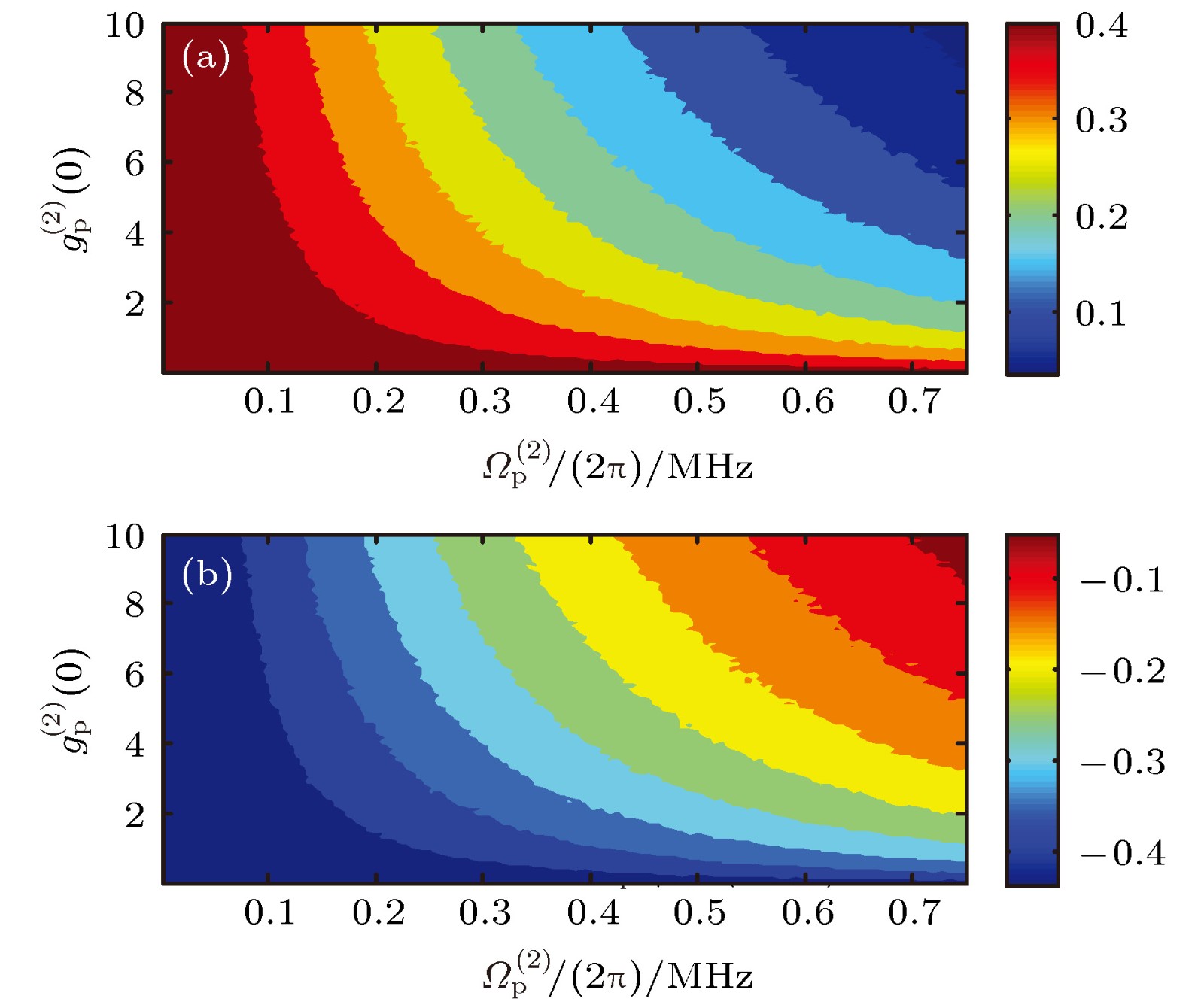
${\phi _{\rm{p}}}\left( L \right)/{\text{π}}$ 作为入射探测场拉比频率${\varOmega _{\rm{p}}}\left( 0 \right)/(2{\text{π}})$ 和初始二阶关联函数$g_{\rm{p}}^{\left( 2 \right)}\left( 0 \right)$ 的函数 (a)探测失谐${\varDelta _{\rm{p}}} = 1.4\;{\rm{MHz}}$ ; (b)探测失谐${\varDelta _{\rm{p}}} = $ $ - 1.4\;{\rm{MHz}}$ . 其他参数同图2Fig. 5. Probe phase
${\phi _{\rm{p}}}\left( L \right)/{\text{π}}$ as a function of the Rabi frequency of the incident probe field${\varOmega _{\rm{p}}}\left( 0 \right)/(2{\text{π}})$ and initial second-order correlation function$g_{\rm{p}}^{\left( 2 \right)}\left( 0 \right)$ : (a) Probe detuning${\varDelta _{\rm{p}}} = 1.4\;{\rm{MHz}}$ ; (b) probe detuning${\varDelta _{\rm{p}}} = $ $- 1.4\;{\rm{MHz}}$ . Other parameters are the same as in Fig. 2.
图 6 探测场相位
${\phi _{\rm{p}}}\left( L \right)/{\text{π}}$ 作为(a)主量子数$n$ 和(b)原子密度$\rho $ 的函数. 入射探测场拉比频率${\varOmega _{\rm{p}}}\left( 0 \right)/$ $(2{\text{π}}) = 0.3\;{\rm{MHz}}$ , 初始二阶关联函数$g_{\rm{p}}^{\left( {\rm{2}} \right)}\left( 0 \right) = 1$ . 其他参数同图2Fig. 6. Probe phase
${\phi _{\rm{p}}}\left( L \right)/{\text{π}}$ as a function of (a)the principal quantum number$n$ and (b) the atomic density$\rho $ . The incident probe intensity${\varOmega _{\rm{p}}}\left( 0 \right)/(2{\text{π}}) = 0.3\;{\rm{MHz}}$ and the initial second-order correlation function$g_{\rm{p}}^{\left( {\rm{2}} \right)}\left( 0 \right) = 1$ . Other parameters are the same as in Fig. 2. -
[1] Harris S E, Field J E, Imamoglu A 1990 Phys. Rev. Lett. 64 1107
Google Scholar
[2] Harris S E 1997 Physics Today 50 36
[3] Fleichhauer M, Imamoglu A, Marangos J P 2005 Rev. Mod. Phys. 77 633
Google Scholar
[4] Kasapi A, Jain M, Yin G Y, Harris S E 1995 Phys. Rev. Lett. 74 2447
Google Scholar
[5] Hau L V, Harris S E, Dutton Z, Behroozi C H 1999 Nature 397 594
Google Scholar
[6] Kash M M, Sautenkov V A, Zibrov A S, Hollberg L, Welch G R, Lukin M D, Rostovtsev Y, Fry E S, Scully M O 1999 Phys. Rev. Lett. 82 5229
Google Scholar
[7] Lukin M D 2003 Rev. Mod. Phys. 75 457
Google Scholar
[8] Fleichhauer M, Lukin M D 2000 Phys. Rev. Lett. 84 5094
Google Scholar
[9] Simon C, Afzelius M, Appel J, de la Giroday A B, Dewhurst S J, Gisin N, Hu C Y, Jelezko F, Kröll S, Müller J H, Nunn J, Polzik E S, Rarity J G, de Riedmatten H, Rosenfeld W, Shields A J, Sköld N, Stevenson R M, Thew R, Walmsley I A, Weber M C, Weinfurter H, Wrachtrup J, Young R J 2010 Eur. Phys. J. D. 58 1
Google Scholar
[10] Eisaman M D, Andre A, Massou M, Fleichhauer M, Zibrov A S, Lukin M D 2005 Nature 438 837
Google Scholar
[11] Chanelière T, Matsukevich D N, Jenkins S D, Lan S Y, Kennedy T A B, Kuzmich A 2005 Nature 438 833
Google Scholar
[12] De Araujo L E E 2010 Opt. Lett. 35 977
Google Scholar
[13] Artoni M, La Rocca G C 2006 Phys. Rev. Lett. 96 073905
Google Scholar
[14] He Q Y, Xue Y, Artoni M, La Rocca G C, Xu J H, Gao J Y 2006 Phys. Rev. B 73 195124
Google Scholar
[15] Schmidt H, Ram R J 2000 App. Phys. Lett. 76 3173
Google Scholar
[16] Wu J H, La Rocca G C, Artoni M 2008 Phys. Rev. B 77 113106
Google Scholar
[17] Friedler I, Petrosyan D, Fleischhauer M, Kurizki G 2005 Phys. Rev. A 72 043803
Google Scholar
[18] Weatherill K J, Pritchard J D, Abel R P, Bason M G, Mohapatra A K, Adams C S 2008 J. Phys. B: At. Mol. Opt. Phys. 41 201002
Google Scholar
[19] Walker T G 2012 Nature 488 39
Google Scholar
[20] Müller M M, Kölle A, Löw R, Pfau T, Calarco T, Montangero S 2013 Phys. Rev. A 87 053412
Google Scholar
[21] Peyronel T, Firstenberg O, Liang Q Y, Hofferberth S, Gorshkov A V, Pohl T, Lukin M D, Vuletic V 2012 Nature 488 57
Google Scholar
[22] Gorniaczyk H, Tresp C, Schmidt J, Fedder H, Hofferberth S 2014 Phys. Rev. Lett. 113 053601
Google Scholar
[23] Chen W, Beck K M, Bücker R, Gullans M, Lukin M D, Tanji-Suzuki H, Vuletić V 2013 Science 341 768
Google Scholar
[24] Baur S, Tiarks D, Rempe G, Dürr S 2014 Phys. Rev. Lett. 112 073901
Google Scholar
[25] Paredes-Barato D, Adams C S 2014 Phys. Rev. Lett. 112 040501
Google Scholar
[26] Pritchard J D, Maxwell D, Gauguet A, Weatherill K J, Jones M P A, Adams C S 2010 Phys. Rev. Lett. 105 193603
Google Scholar
[27] Sevinçli S, Henkel N, Ates C, Pohl T 2011 Phys. Rev. Lett. 107 153001
Google Scholar
[28] Petrosyan D, Otterbach J, Fleischhauer M 2011 Phys. Rev. Lett. 107 213601
Google Scholar
[29] Yan D, Liu Y M, Bao Q Q, Fu C B, Wu J H 2012 Phys. Rev. A 86 023828
Google Scholar
[30] Yan D, Cui C L, Liu Y M, Song L J, Wu J H 2013 Phys. Rev. A 87 023827
Google Scholar
[31] Liu Y M, Yan D, Tian X D, Cui C L, Wu J H 2014 Phys. Rev. A 89 033839
Google Scholar
[32] Liu Y M, Tian X D, Yan D, Zhang Y, Cui C L, Wu J H 2015 Phys. Rev. A 91 043802
Google Scholar
[33] Liu Y M, Tian X D, Wang X, Yan D, Wu J H 2016 Opt. Lett. 408 41
[34] Singer K, Stanojevic J, Weidemuller M, Cote R 2005 J. Phys. B: At. Mol. Opt. Phys. 38 S295
Google Scholar
下载:
计量
- 文章访问数: 8982
- PDF下载量: 154
- 被引次数: 0
