-
In recent years, biomolecular motors have received widespread attention. Biomolecular motors are biological macromolecules that convert chemical energy into mechanical energy. The biomolecular motor is only a few tens of nanometers in size. According to Brownian theory of motion, people have constructed different types of Brownian ratchet models, such as rocking ratchets and closed-loop control ratchets. In previous studies, the directional transportation of Brownian ratchet is affected by conservative forces. These conservative forces include constant force, elastic force or harmonic force. However, whether the ratchet system can produce directional motion under the action of non-conservative forces is still rarely studied. Owing to the complex environment in the organism, for the studies of two-dimensional systems, the transport behavior of molecular motor has not been fully explained. Therefore, it is more practical to study the transport of Brownian particles in a two-dimensional ratchet potential. The directional transport of two-dimensional Brownian particles subjected to conservative forces and non-conservative forces are studied in this work. It is found that the non-conservative external force has the effect of promoting the directional transport of coupling ratchets. With the change of the free length of the spring and spring coefficient, the average velocity of the coupled particles can be reversed. This means that the coupling effect can induce the inversion of two-dimensional Brownian ratchets. At the same time, the reverse transportation of coupled particles is enhanced under the interaction effect of conservative forces (spring elasticity) and non-conservative external forces. By choosing different kinds of external forces (conserved and non-conserved), in the experiment, it is possible to provide new method of separating two-dimensional coupled Brownian particles. -
Keywords:
- Brownian particles /
- nonconserved forces /
- mean velocity /
- flow reversal
[1] 舒咬根, 欧阳钟灿 2007 自然杂志 5 249
Google Scholar
Shu Y G, Ouyang Z C 2007 Chin. J. Nat. 5 249
Google Scholar
[2] 舒咬根, 欧阳钟灿 2007 物理 10 735
Google Scholar
Shu Y G, Ouyang Z C 2007 Physics 10 735
Google Scholar
[3] 国家自然科学基金委员会, 中国科学院 2020 中国学科发展战略·软凝聚态物理学(下) (北京: 科学出版社) 第1037页
National Natural Science Foundation of China, Chinese Academy of Sciences 2020 Chinese Subject Development Strategy · Soft Condensed Matter Physics (Part 2) (Beijing: Science Press) p1037 (in Chinese)
[4] Wu J, Zhou J, Ai B 2016 Physica A 462 864
Google Scholar
[5] 耿轶钊, 晏世伟 2016 物理学进展 36 157
Google Scholar
Geng Y Z, Yan S W 2016 Prog. Phys. 36 157
Google Scholar
[6] 卓益忠, 赵同军, 展永 2000 物理 12 712
Google Scholar
Zhuo Y Z, Zhao T J, Zhan Y 2000 Physics 12 712
Google Scholar
[7] 舒咬根 2004 博士学位论文 (厦门: 厦门大学)
Shu Y G 2004 Ph. D. Dissertation (Xiamen: Xiamen University) (in Chinese)
[8] 刘芳 2011 硕士学位论文 (秦皇岛: 燕山大学)
Liu F 2011 M. S. Thesis (Qinhuangdao: Yanshan University) (in Chinese)
[9] Van den Heuvel M G L, Dekker C 2007 Science 317 333
Google Scholar
[10] Bartussek R, Hänggi P, Kissner J G 1994 Eur. Phys. Lett. 28 459
Google Scholar
[11] Zhang H W, Wen S T, Zhang H T, Li Y X, Chen G R 2012 Chin. Phys. B 21 078701
Google Scholar
[12] Bao J D, Zhuo Y Z 1998 Phys. Lett. A 239 228
Google Scholar
[13] Doering C R 1995 Il Nuovo Cimento D 17 685
Google Scholar
[14] Bartussek R, Reimann P, Hänggi P 1996 Phys. Rev. Lett. 76 1166
Google Scholar
[15] Gao T F, Chen J C 2009 J. Phys. A: Math. Theor. 42 065002
Google Scholar
[16] 吴魏霞, 郑志刚 2013 62 135
Google Scholar
Wu W X, Zheng Z G 2013 Acta Phys. Sin. 62 135
Google Scholar
[17] 吴魏霞, 宋艳丽, 韩英荣 2015 64 17
Google Scholar
Wu W X, Song Y L, Han Y R 2015 Acta Phys. Sin. 64 17
Google Scholar
[18] 谢天婷, 邓科, 罗懋康. 2016 65 7
Google Scholar
Xie T T, Deng K, Luo M K 2016 Acta Phys. Sin. 65 7
Google Scholar
[19] 刘红梅, 汪瑜 2014 物理通报 10 129
Google Scholar
[20] 马文蔚 2008 物理学(上册) 第五版 (北京: 高等教育出版社) 第75页
[21] Tomé T 2010 Phys. Rev. E 82 021120
Google Scholar
[22] Tomé T 2006 Braz. J. Phys. 36 1285
Google Scholar
[23] Ai B Q, Chen Q Y, He Y F, Li F G, Zhong W R 2013 Phys. Rev. E 88 062129
Google Scholar
[24] Li C P, Chen H B, Zheng Z G 2017 Front. Phys. 12 1
Google Scholar
[25] Romanczuk P, Müller F, Schimansky-Geier L 2010 Phys. Rev. E 81 061120
Google Scholar
[26] Wang H Y, Bao J D 2007 Physica A 374 33
Google Scholar
[27] Shubeita G T, Tran S L, Xu J, Vershinin M, Cermelli S, Cotton S L, Welte M A, Gross S P 2008 Cell 135 1098
Google Scholar
[28] Hill D B, Plaza M J, Bonin K, Holzwarth G 2004 Eur. Biophys. J 33 623
Google Scholar
[29] Mallik R, Petrov D, Lex S A, King S J, Gross S P 2005 Curr. Biol. 15 2075
Google Scholar
[30] Bao J D 2001 Phys. Rev. E 63 061112
Google Scholar
[31] Ai B 2017 Phys. Rev. E 96 012131
Google Scholar
[32] Luo Y H, Zeng C H, Ai B Q 2020 Phys. Rev. E 102 042114
Google Scholar
[33] He Y F, Ai B Q, Dai C X 2020 Phys. Rev. Lett. 124 075001
Google Scholar
-
图 1 二维棘轮外势
$ V(x, y) $ 的结构示意图Figure 1. The schematic diagram of two-dimensional ratchet potential
$ V(x, y) $ .
图 2 非保守外力
$ {F_x} $ 和$ {F_y} $ 的结构示意图, 非保守力参量$ a = 0.4 $ Figure 2. The schematic diagram of non-conservative forces
$ {F_x} $ and$ {F_y} $ , where non-conservative force parameter$ a = 0.4 $ .
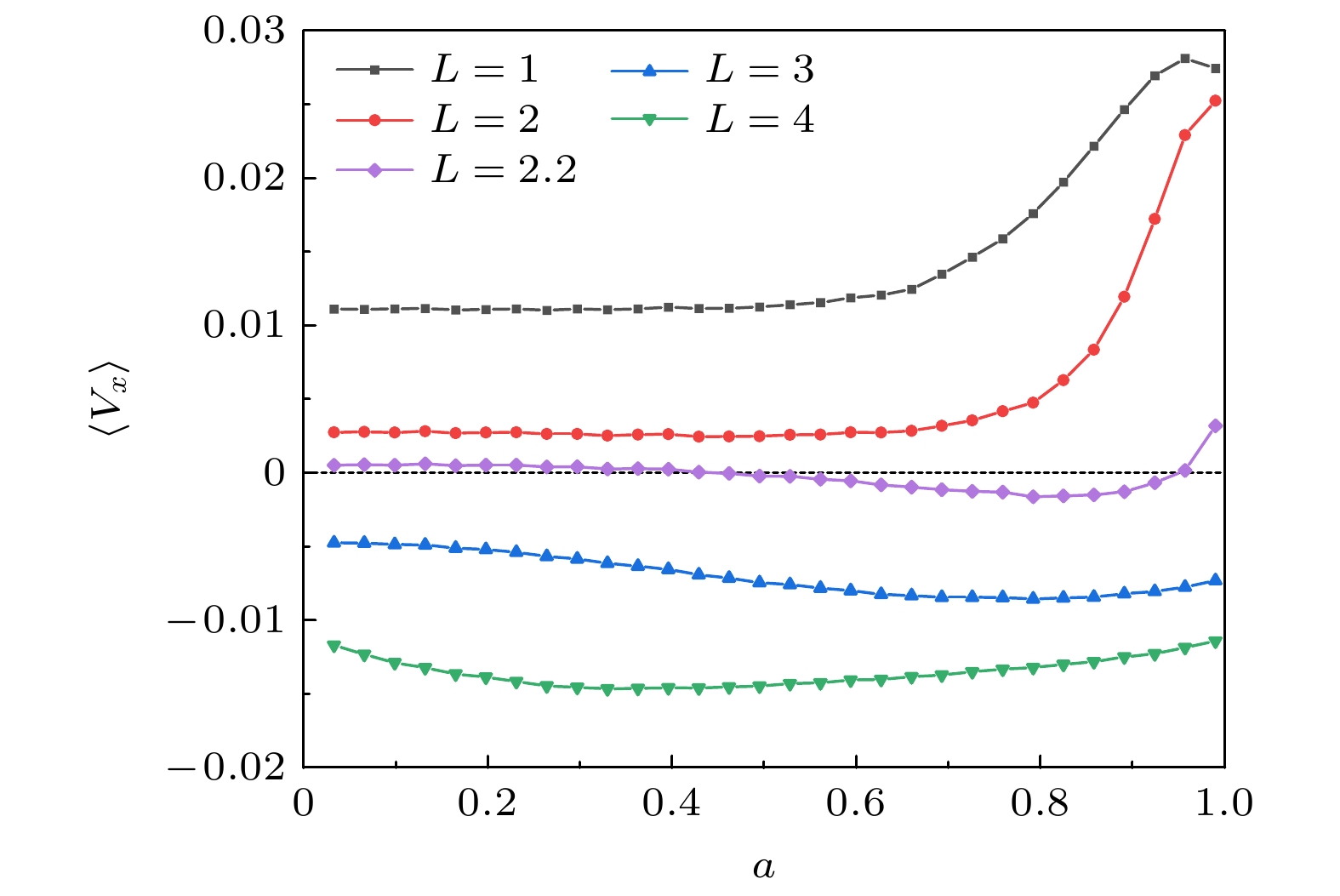
图 3 不同弹簧原长
$ L $ 下平均速度$ \left\langle {{V_x}} \right\rangle $ 随非保守力参数$ a $ 的变化曲线, 其中$ D = 0.1 $ ,$ k = 2 $ Figure 3. The curves of the mean velocity
$ \left\langle {{V_x}} \right\rangle $ varying with the non-conservative force parameter$ a $ under different original length of the spring L, where$ D = 0.1 $ ,$ k = 2 $ .
图 4 非保守力
$ {F_x} $ 随参数$ a $ 的变化曲线Figure 4. The curve of the non-conservative force
$ {F_x} $ varying with the parameter$ a $ .
图 5 不同噪声强度
$ D $ 下平均速度$ \left\langle {{V_x}} \right\rangle $ 随弹簧原长$ L $ 的变化曲线, 其中$ a = 0.4 $ ,$ k = 2 $ Figure 5. The curves of the mean velocity
$ \left\langle {{V_x}} \right\rangle $ varying with the original length of the spring$ L $ under different noise intensity$ D $ , where$ a = 0.4 $ ,$ k = 2 $ .
图 6 耦合粒子的位置随时间演化图像, 其中
$ a = 0.4 $ ,$ k = 2 $ ,$ L = 3.5 $ ,$ D = 0.1 $ Figure 6. Trajectories for the coupled particles as a function of time, where
$ a = 0.4 $ ,$ k = 2 $ ,$ L = 3.5 $ ,$ D = 0.1 $ .
图 7 不同耦合强度下平均速度
$ \left\langle {{V_x}} \right\rangle $ 随热噪声$ D $ 的变化曲线, 其中$ a = 0.4 $ ,$ L = 1 $ Figure 7. The curves of the mean velocity
$ \left\langle {{V_x}} \right\rangle $ varying with the noise$ D $ under different coupling strength, where$ a = 0.4 $ ,$ L = 1 $ .
图 8 不同非保守外力参量
$ a $ 下平均速度$ \left\langle {{V_x}} \right\rangle $ 随弹性系数$ k $ 的变化曲线, 其中$ D = 0.1 $ ,$ L = 1 $ Figure 8. The curves of the mean velocity
$ \left\langle {{V_x}} \right\rangle $ varying with the spring coefficient$ k $ under different non-conservative force parameter$ a $ , where$ D = 0.1 $ ,$ L = 1 $ .
图 9 耦合粒子的位置随时间演化图像, 其中
$ a = 0.3 $ ,$ k = 0.3 $ ,$ L = 1 $ ,$ D = 0.1 $ Figure 9. Trajectories for the coupled particles as a function of time, where
$ a = 0.3 $ ,$ k = 0.3 $ ,$ L = 1 $ ,$ D = 0.1 $ . -
[1] 舒咬根, 欧阳钟灿 2007 自然杂志 5 249
Google Scholar
Shu Y G, Ouyang Z C 2007 Chin. J. Nat. 5 249
Google Scholar
[2] 舒咬根, 欧阳钟灿 2007 物理 10 735
Google Scholar
Shu Y G, Ouyang Z C 2007 Physics 10 735
Google Scholar
[3] 国家自然科学基金委员会, 中国科学院 2020 中国学科发展战略·软凝聚态物理学(下) (北京: 科学出版社) 第1037页
National Natural Science Foundation of China, Chinese Academy of Sciences 2020 Chinese Subject Development Strategy · Soft Condensed Matter Physics (Part 2) (Beijing: Science Press) p1037 (in Chinese)
[4] Wu J, Zhou J, Ai B 2016 Physica A 462 864
Google Scholar
[5] 耿轶钊, 晏世伟 2016 物理学进展 36 157
Google Scholar
Geng Y Z, Yan S W 2016 Prog. Phys. 36 157
Google Scholar
[6] 卓益忠, 赵同军, 展永 2000 物理 12 712
Google Scholar
Zhuo Y Z, Zhao T J, Zhan Y 2000 Physics 12 712
Google Scholar
[7] 舒咬根 2004 博士学位论文 (厦门: 厦门大学)
Shu Y G 2004 Ph. D. Dissertation (Xiamen: Xiamen University) (in Chinese)
[8] 刘芳 2011 硕士学位论文 (秦皇岛: 燕山大学)
Liu F 2011 M. S. Thesis (Qinhuangdao: Yanshan University) (in Chinese)
[9] Van den Heuvel M G L, Dekker C 2007 Science 317 333
Google Scholar
[10] Bartussek R, Hänggi P, Kissner J G 1994 Eur. Phys. Lett. 28 459
Google Scholar
[11] Zhang H W, Wen S T, Zhang H T, Li Y X, Chen G R 2012 Chin. Phys. B 21 078701
Google Scholar
[12] Bao J D, Zhuo Y Z 1998 Phys. Lett. A 239 228
Google Scholar
[13] Doering C R 1995 Il Nuovo Cimento D 17 685
Google Scholar
[14] Bartussek R, Reimann P, Hänggi P 1996 Phys. Rev. Lett. 76 1166
Google Scholar
[15] Gao T F, Chen J C 2009 J. Phys. A: Math. Theor. 42 065002
Google Scholar
[16] 吴魏霞, 郑志刚 2013 62 135
Google Scholar
Wu W X, Zheng Z G 2013 Acta Phys. Sin. 62 135
Google Scholar
[17] 吴魏霞, 宋艳丽, 韩英荣 2015 64 17
Google Scholar
Wu W X, Song Y L, Han Y R 2015 Acta Phys. Sin. 64 17
Google Scholar
[18] 谢天婷, 邓科, 罗懋康. 2016 65 7
Google Scholar
Xie T T, Deng K, Luo M K 2016 Acta Phys. Sin. 65 7
Google Scholar
[19] 刘红梅, 汪瑜 2014 物理通报 10 129
Google Scholar
[20] 马文蔚 2008 物理学(上册) 第五版 (北京: 高等教育出版社) 第75页
[21] Tomé T 2010 Phys. Rev. E 82 021120
Google Scholar
[22] Tomé T 2006 Braz. J. Phys. 36 1285
Google Scholar
[23] Ai B Q, Chen Q Y, He Y F, Li F G, Zhong W R 2013 Phys. Rev. E 88 062129
Google Scholar
[24] Li C P, Chen H B, Zheng Z G 2017 Front. Phys. 12 1
Google Scholar
[25] Romanczuk P, Müller F, Schimansky-Geier L 2010 Phys. Rev. E 81 061120
Google Scholar
[26] Wang H Y, Bao J D 2007 Physica A 374 33
Google Scholar
[27] Shubeita G T, Tran S L, Xu J, Vershinin M, Cermelli S, Cotton S L, Welte M A, Gross S P 2008 Cell 135 1098
Google Scholar
[28] Hill D B, Plaza M J, Bonin K, Holzwarth G 2004 Eur. Biophys. J 33 623
Google Scholar
[29] Mallik R, Petrov D, Lex S A, King S J, Gross S P 2005 Curr. Biol. 15 2075
Google Scholar
[30] Bao J D 2001 Phys. Rev. E 63 061112
Google Scholar
[31] Ai B 2017 Phys. Rev. E 96 012131
Google Scholar
[32] Luo Y H, Zeng C H, Ai B Q 2020 Phys. Rev. E 102 042114
Google Scholar
[33] He Y F, Ai B Q, Dai C X 2020 Phys. Rev. Lett. 124 075001
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4070
- PDF Downloads: 91
- Cited By: 0
