-
Biological molecular motors exist in cells widely. They can make use of intracellular free energy to complete all kinds of internal biological transports by transforming chemical energy into mechanical energy. The kind of directional movement of biological molecular motors plays a very important role in intracellular material transportation. In order to study the transport mechanism of molecular motors further, a large number of ratchet models are proposed, such as rocking ratchets and flashing ratchets. By investigating various kinds of ratchets we can not only understand the directional movement mechanism of Brownian particles, but can find suitable conditions in which the performance of Brownian motors’ directional transportation could be enhanced. Meanwhile, the investigation of ratchets could also be applied in manufacturing nanometer devices. At present, the directional transportation of Brownian ratchet has attracted extensive interests of researchers. In general, most friction factors of Brownian ratchet models are considered unit. In fact, the concentration of solutions and cell fluid impurity affect the actual frictional damping conditions, so the real frictional coefficient of Brownian motors is often changed. In addition, lots of experimental studies have shown that the movement of Brownian motors is collectively directed motion and the kind of directional movement is induced by intermolecular coupling interaction. As a result, it is more valuable to investigate the transporting performance of coupled Brownian particles that existed in different frictional damping conditions. In order to enhance the transporting performance of Brownian ratchet in different frictional damping conditions, we discuss how the frictional damping factor influences the directional movement of coupled Brownian particles deeply when Brownian particles drag loads. In this paper, we established the overdamped frictional ratchets, and then we investigated how frictional damping coefficient ratio, coupling strength and external force amplitude affect the transportation of coupled Brownian ratchets. On the basis of the investigation, some interesting results are found. The directional transport of frictional ratchets can be promoted by adjusting the frictional damping factor. Besides, the transportation can obtain the maximum under the appropriate friction factor case. In addition, under certain frictional damping condition, the directional transportation of the friction ratchets present multi-peak structure as the external force amplitude increases. Meanwhile, the appropriate free length and coupling strength can also enhance the transportation characteristic of frictional ratchets. All conclusions obtained in this paper can not be applied in selecting suitable frictional damping conditions experimentally to improve the directional transportation of coupled Brownian ratchets, but they can also be used in developing and manufacturing nanometer devices. -
Keywords:
- coupled Brownian motors /
- asymmetric friction /
- average velocity
[1] Xie P 2010 Int. J. Biol. Sci. 6 665
[2] 舒咬根, 欧阳钟灿 2007 物理 36 735
Google Scholar
Shu Y G, Ouyang Z C 2007 Physics 36 735
Google Scholar
[3] Matsuda A, Li J, Brumm P, Adachi T, Inoue Y, Kim T 2019 Biolphys. J. 116 2161
Google Scholar
[4] Brown A I, Sivak D A 2019 Europhys. Lett. 126 40004
Google Scholar
[5] Grossert C, Leder M, Denisov S, Hänggi P, Weitz M 2016 Nat. Commun. 7 10440
Google Scholar
[6] Lee A K, Lee J R, Lee K H 2012 Physica B 407 4298
Google Scholar
[7] Wickenbrock A, Cubero D, Wahab N A A, Phoonthong P, Renzoni F 2011 Phys. Rev. E 84 021127
Google Scholar
[8] Lade S J 2010 J. Phys. A: Math. Theor. 43 249801
Google Scholar
[9] Ethier S N, Lee J L 2018 R. Soc. OpenSci. 5 171685
Google Scholar
[10] Vorotnikov D 2013 J. Math. Biol. 68 1677
[11] Roca F, Villaluenga J P G, Dinis L 2014 Europhys. Lett. 107 10006
Google Scholar
[12] Bao J D 2018 College Physics 37 11
[13] Huang S N, Zhu W J, Huang X Q, Ai B Q, Li F G 2019 Chin. Phys. B 28 040502
Google Scholar
[14] 艾保全, 王先菊, 刘国涛, 刘良钢, 郑华 2001 中山大学学报: 自然科学版 40 27
Ai B Q, Wang X J, Liu G T, Liu L G, Zheng H 2001 ActaSci. Natur. Univ. Sunyatseni 40 27
[15] 吕明涛, 延明月, 艾保全, 高天附, 郑志刚 2017 66 220501
Google Scholar
Lv M T, Yan M Y, Ai B Q, Gao T F, Zheng Z G 2017 Acta. Phys. Sin. 66 220501
Google Scholar
[16] Holmes H R, Böhringer K F 2018 Adv. Colloid. Interface. Sci. 255 18
Google Scholar
[17] Latorre J C, Kramer P R, Pavliotis G A 2014 J. Comput. Phys. 257 57
Google Scholar
[18] Ryabov A, Holubec V, Yaghoubi M H, Varga M, Foulaadvand M E, Chvosta P 2016 J. Stat. Mech.: Theory Exp. 2016 093202
Google Scholar
[19] Radtke M, Patzelt A, Knorr F, Lademann J, Netz R R 2017 Eur. J. Pharm. Biopharm. 116 125
Google Scholar
[20] Hojo M, Arai N, Ebisuzaki T 2018 Mol. Simul. 44 523
Google Scholar
[21] Pattanayak S, Das R, Kumar M, Mishra S 2019 Eur. Phys. J. E 42 62
Google Scholar
[22] 延明月, 张旭, 刘晨昊, 黄仁忠, 高天附, 郑志刚 2018 67 190501
Google Scholar
Yan M Y, Zhang X, Liu C H, Huang R Z, Gao T F, Zheng Z G 2018 Acta Phys. Sin. 67 190501
Google Scholar
[23] Lombardo J, Broadwater D, Collins R, Cebe K, Brady R, Harrison S 2019 Hum. Pathol. 86 129
Google Scholar
[24] Toyoshima H 1951 J. Japn. Fores. Soc. 33 203
[25] Toyoshima H 1951 J. Japn. Fores. Soc. 33 83
[26] Pascu M N, Popescu I 2016 Stoch. Proc. Appl. 126 628
Google Scholar
[27] Jacka S D, Mijatović A, Širaj D 2014 Stoch. Proc. Appl. 124 1055
Google Scholar
[28] Atzberger P J 2006 Phys. Lett. A 351 225
Google Scholar
[29] Guo W, Du L C, Liu Z Z, Yang H, Mei D C 2017 Chin. Phys. B 26 010502
Google Scholar
[30] von Gehlen S, Evstigneev M, Reimann P 2009 Phys. Rev. E 79 031114
Google Scholar
[31] Saikia S, Mahato M C 2010 Physica A 389 4052
Google Scholar
[32] von Gehlen S, Evstigneev M, Reimann P 2008 Phys. Rev. E 77 031106
Google Scholar
-
图 1 摩擦对称性破缺耦合粒子的模型示意图
Figure 1. Coupling particles model with broken friction symmetry.
图 2 耦合粒子的平均速度
$\left\langle v \right\rangle$ 随弹簧自由长度l的变化曲线, 其中γ1 = 5.0, k = 20.0, α = 0.3, A = 1.0, λ = 0.1Figure 2. The average velocity
$\left\langle v \right\rangle$ of coupled particles varying with the free length l, where${\gamma _1} = 5.0$ ,$k = 20.0$ ,$\alpha = 0.3$ ,$A = 1.0$ ,$\lambda = 0.1$ .
图 3 耦合粒子的平均速度
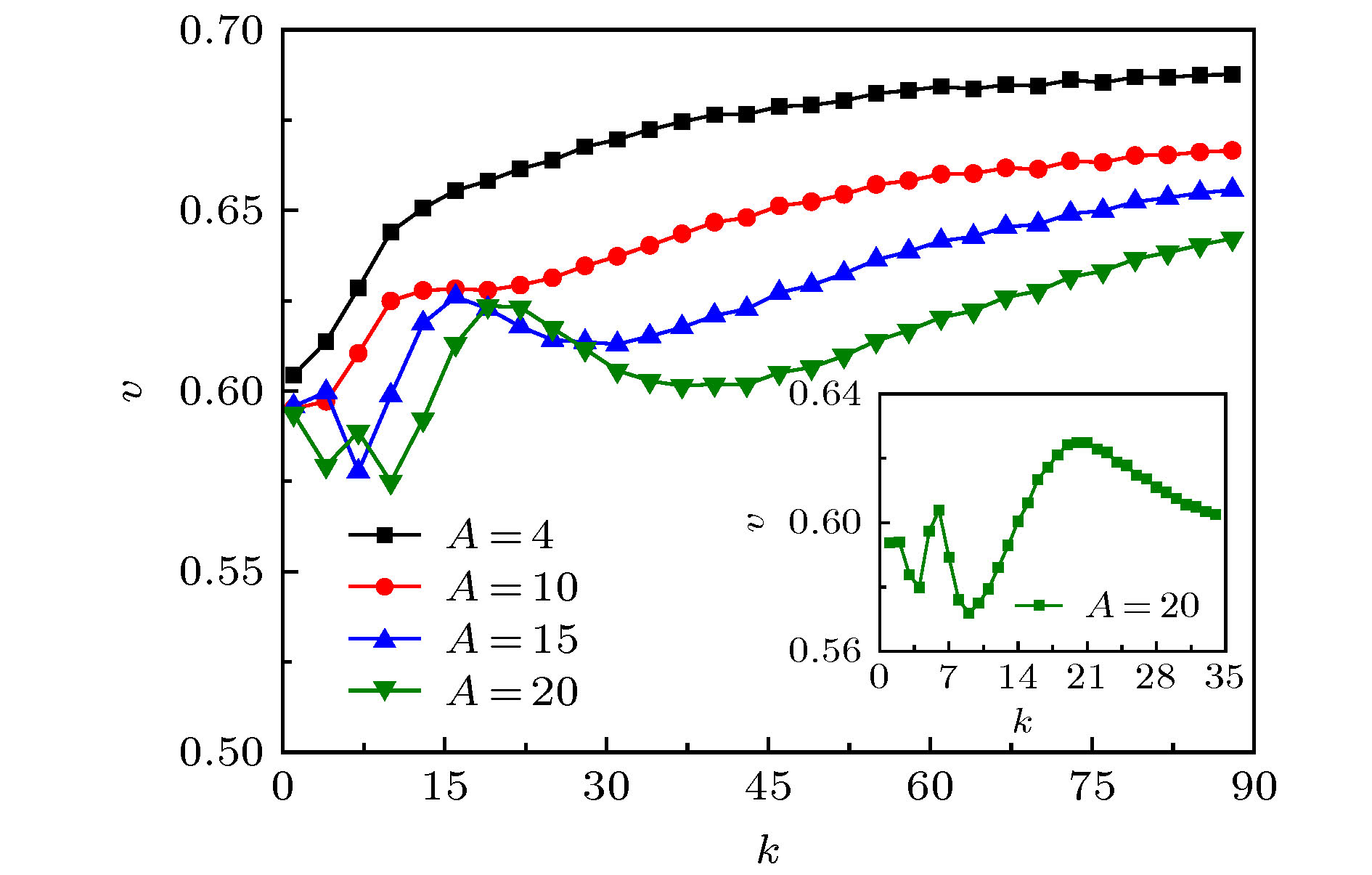
$\left\langle v \right\rangle$ 随耦合强度k的变化曲线, 插图为$A = 20.0$ 时的变化曲线, 其中${\gamma _1} = 5.0$ ,$l = 0.25$ ,$\alpha = 0.3$ ,$D = 0.35$ ,$\lambda = 0.1$ Figure 3. The average velocity
$\left\langle v \right\rangle$ of coupled particles varying with the strength of coupling k, the insert figure described the average velocity curve when$A = 20.0$ , where${\gamma _1} = 5.0$ ,$l = 0.25$ ,$\alpha = 0.3$ ,$D = 0.35$ ,$\lambda = 0.1$ .
图 4 耦合粒子的平均速度
$\left\langle v \right\rangle$ 随外力振幅A的变化曲线, 其中γ1 = 5.0, l = 0.25, k = 20.0, D = 0.35, λ = 0.1Figure 4. The average velocity
$\left\langle v \right\rangle$ of coupled particles varying with the amplitude A of external force, where${\gamma _1} = 5.0$ ,$l = 0.25$ ,$k = 20.0$ ,$D = 0.35$ ,$\lambda = 0.1$ .
图 5 耦合粒子的平均速度
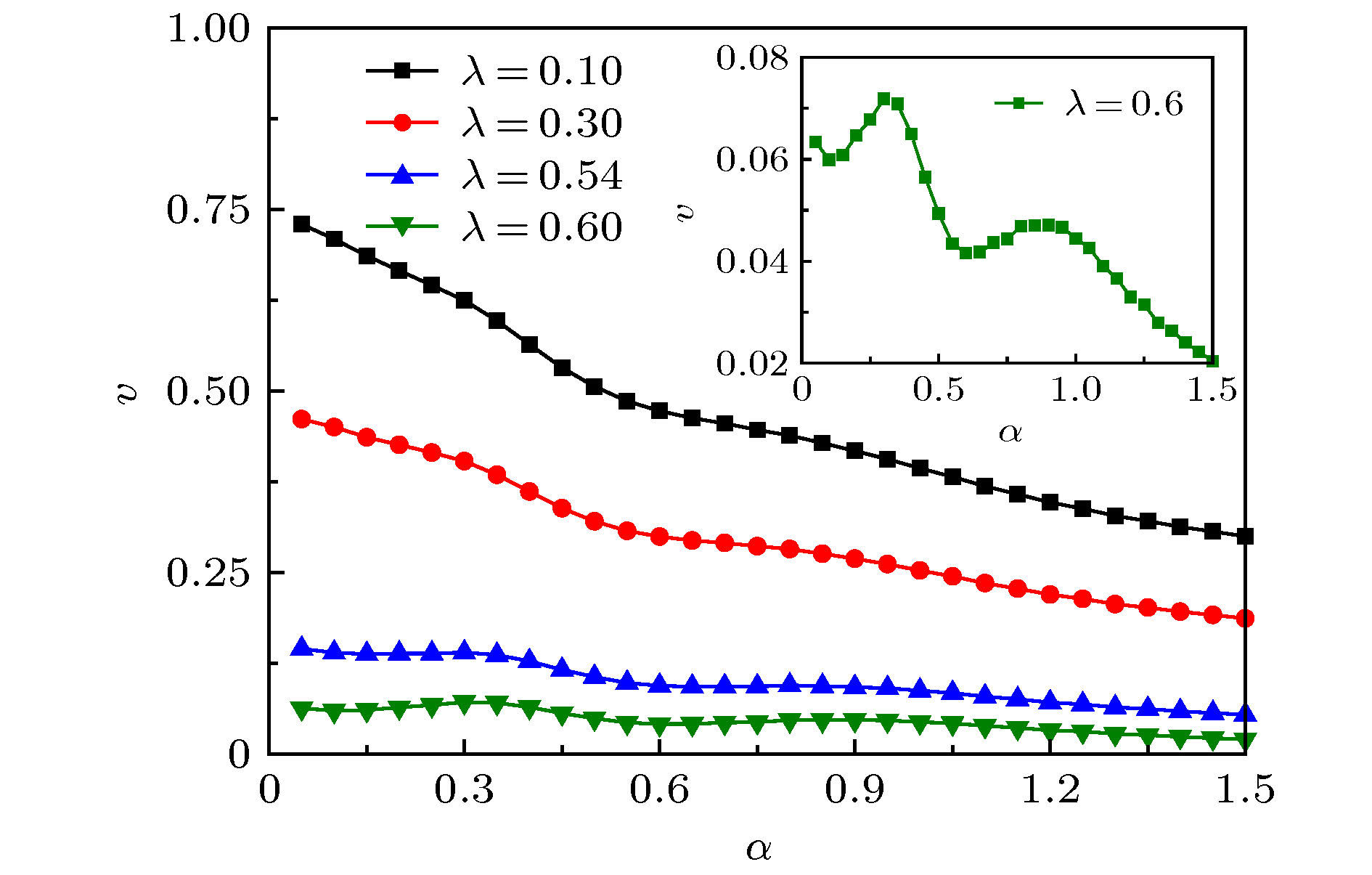
$\left\langle v \right\rangle$ 随摩擦阻尼系数比$\alpha$ 的变化曲线, 插图为$\lambda = 0.6$ 时的变化曲线, 其中${\gamma _1} = 5.0$ ,$k = 20.0$ ,$l = 0.25$ ,$A = 20.0$ ,$D = 0.35$ Figure 5. The average velocity
$\left\langle v \right\rangle$ of coupled particles varying with the frictional damping coefficient ratio$\alpha$ , the insert figure described the average velocity curve when$\lambda = 0.6$ , where${\gamma _1} = 5.0$ ,$k = 20.0$ ,$l = 0.25$ ,$A = 20.0$ ,$D = 0.35$ . -
[1] Xie P 2010 Int. J. Biol. Sci. 6 665
[2] 舒咬根, 欧阳钟灿 2007 物理 36 735
Google Scholar
Shu Y G, Ouyang Z C 2007 Physics 36 735
Google Scholar
[3] Matsuda A, Li J, Brumm P, Adachi T, Inoue Y, Kim T 2019 Biolphys. J. 116 2161
Google Scholar
[4] Brown A I, Sivak D A 2019 Europhys. Lett. 126 40004
Google Scholar
[5] Grossert C, Leder M, Denisov S, Hänggi P, Weitz M 2016 Nat. Commun. 7 10440
Google Scholar
[6] Lee A K, Lee J R, Lee K H 2012 Physica B 407 4298
Google Scholar
[7] Wickenbrock A, Cubero D, Wahab N A A, Phoonthong P, Renzoni F 2011 Phys. Rev. E 84 021127
Google Scholar
[8] Lade S J 2010 J. Phys. A: Math. Theor. 43 249801
Google Scholar
[9] Ethier S N, Lee J L 2018 R. Soc. OpenSci. 5 171685
Google Scholar
[10] Vorotnikov D 2013 J. Math. Biol. 68 1677
[11] Roca F, Villaluenga J P G, Dinis L 2014 Europhys. Lett. 107 10006
Google Scholar
[12] Bao J D 2018 College Physics 37 11
[13] Huang S N, Zhu W J, Huang X Q, Ai B Q, Li F G 2019 Chin. Phys. B 28 040502
Google Scholar
[14] 艾保全, 王先菊, 刘国涛, 刘良钢, 郑华 2001 中山大学学报: 自然科学版 40 27
Ai B Q, Wang X J, Liu G T, Liu L G, Zheng H 2001 ActaSci. Natur. Univ. Sunyatseni 40 27
[15] 吕明涛, 延明月, 艾保全, 高天附, 郑志刚 2017 66 220501
Google Scholar
Lv M T, Yan M Y, Ai B Q, Gao T F, Zheng Z G 2017 Acta. Phys. Sin. 66 220501
Google Scholar
[16] Holmes H R, Böhringer K F 2018 Adv. Colloid. Interface. Sci. 255 18
Google Scholar
[17] Latorre J C, Kramer P R, Pavliotis G A 2014 J. Comput. Phys. 257 57
Google Scholar
[18] Ryabov A, Holubec V, Yaghoubi M H, Varga M, Foulaadvand M E, Chvosta P 2016 J. Stat. Mech.: Theory Exp. 2016 093202
Google Scholar
[19] Radtke M, Patzelt A, Knorr F, Lademann J, Netz R R 2017 Eur. J. Pharm. Biopharm. 116 125
Google Scholar
[20] Hojo M, Arai N, Ebisuzaki T 2018 Mol. Simul. 44 523
Google Scholar
[21] Pattanayak S, Das R, Kumar M, Mishra S 2019 Eur. Phys. J. E 42 62
Google Scholar
[22] 延明月, 张旭, 刘晨昊, 黄仁忠, 高天附, 郑志刚 2018 67 190501
Google Scholar
Yan M Y, Zhang X, Liu C H, Huang R Z, Gao T F, Zheng Z G 2018 Acta Phys. Sin. 67 190501
Google Scholar
[23] Lombardo J, Broadwater D, Collins R, Cebe K, Brady R, Harrison S 2019 Hum. Pathol. 86 129
Google Scholar
[24] Toyoshima H 1951 J. Japn. Fores. Soc. 33 203
[25] Toyoshima H 1951 J. Japn. Fores. Soc. 33 83
[26] Pascu M N, Popescu I 2016 Stoch. Proc. Appl. 126 628
Google Scholar
[27] Jacka S D, Mijatović A, Širaj D 2014 Stoch. Proc. Appl. 124 1055
Google Scholar
[28] Atzberger P J 2006 Phys. Lett. A 351 225
Google Scholar
[29] Guo W, Du L C, Liu Z Z, Yang H, Mei D C 2017 Chin. Phys. B 26 010502
Google Scholar
[30] von Gehlen S, Evstigneev M, Reimann P 2009 Phys. Rev. E 79 031114
Google Scholar
[31] Saikia S, Mahato M C 2010 Physica A 389 4052
Google Scholar
[32] von Gehlen S, Evstigneev M, Reimann P 2008 Phys. Rev. E 77 031106
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 6101
- PDF Downloads: 116
- Cited By: 0
