-
在活性布朗粒子系统中, 速度的自发对齐是可实现的, 但其机制及影响因素尚需进一步研究. 本文主要探讨了具有吸引性相互作用的活性布朗粒子系统中的团簇行为和自发全局速度对齐现象. 吸引性相互作用和自推进作用的耦合导致粒子趋向于与周围粒子速度对齐. 通过数值模拟, 本文发现自推进作用与吸引性相互作用之间的竞争显著影响团簇的形成及其结构, 系统中会出现网状团簇、块状团簇、粒子离散分布或形成不稳定团簇, 并进而影响自发速度对齐程度. 其中, 块状团簇结构最有利于自发速度对齐的实现. 随着自推进作用在竞争中逐渐占优, 中低填充分数系统中速度对齐程度呈现增加-稳定-下降的趋势, 而高填充分数系统则表现为先稳定后下降的趋势. 系统形成单一块状团簇时, 能够实现自发全局速度对齐.
Spontaneous velocity alignment can occur in active particle systems. As a fundamental inter-particle interaction, the attractive interaction is shown to significantly affect the collective behavior of active particles. However, the mechanisms by which attractive interactions induce and affect velocity alignment are still unclear. To solve this problem, we conduct numerical simulations by using the stochastic Euler method to investigate cluster behavior and spontaneous global velocity alignment in active particle systems with attractive interactions. The local area fraction of particles and its corresponding probability distribution function are computed to capture the system’s cluster behavior. The global velocity alignment order parameter and the polar average parameter are also calculated to characterize the particle velocity directions. Based on whether motion-induced phase separation and crystallization can be achieved, the system is categorized into low, medium, and high packing fraction regimes, and the cluster behavior and velocity alignment within each regime are systematically investigated. Spontaneous velocity alignment results from the coupling of self-propulsion and attractive interactions. During the persistent time, feedback regulation involving particle velocities, relative positions, and interaction forces operates simultaneously among neighboring particles. This process leads to the alignment of particle velocities with those of their neighbors, ultimately achieving large-scale alignment. The closer the particles’ arrangement, the more conducive it is to the coupling of self-propulsion and spatial interactions, thus promoting large-scale spontaneous velocity alignment. The competition between these two effects governs the formation and structure of clusters, ultimately affecting global velocity alignment. At low and medium packing fractions, when the attractive interaction dominates and self-propulsion is negligible, particles attract each other to form discrete banded clusters due to the strong attraction and limited range of interaction. Over time, these clusters connect to form a network-like cluster. Small differences in particle velocity are amplified by the banded structure, hindering velocity alignment. In the systems with low packing fractions, a thin network-like cluster forms, whereas in systems with medium packing fractions, a thicker network-like cluster forms, leading to lower velocity alignment in the former. As self-propulsion becomes more dominant, the network structure loosens, causing the particle bands to break and reconnect until a more stable block-like cluster structure is formed. The system transitions from a network-like cluster to a block-like cluster, with particles becoming closely packed, resulting in global velocity alignment. When self-propulsion dominates and attraction is negligible, particle motion is mainly driven by self-propulsion, resulting in sparse particle distribution or unstable clusters, leading to disordered velocity. Thus, as self-propulsion competes with attractive interactions and becomes dominant, the global velocity alignment increases from low values to a higher plateau and then decreases, approaching zero. At high packing fractions, the initial distribution of particles is dense. Even when the attractive interaction dominates and self-propulsion is negligible, the system forms a block-like cluster, leading to global velocity alignment. As self-propulsion becomes dominant, the instability of the clusters partially hinders spontaneous velocity alignment. Nevertheless, the particles remain densely packed, resulting in local velocity alignment. Thus, as self-propulsion transitions from weak to dominant in competition with attractive interactions, global velocity alignment first plateaus at a higher value, then decreases, but remains above 0.5. It is important to note that the spontaneous velocity alignment discussed here exhibits a finite size effect. In experimental setups and applications involving active particles, smaller systems are usually studied. By modulating the balance between self-propulsion and attractive interactions in these systems, a broader range of spontaneous velocity alignment can be achieved, which may even lead to global velocity alignment. -
Keywords:
- active Brownian particles /
- cluster behavior /
- spontaneous velocity alignment /
- global velocity alignment
[1] Emlen J T 1952 The Auk 69 160
 Google Scholar
Google Scholar
[2] Becco C, Vandewalle N, Delcourt J, Poncin P 2006 Phys. A 367 487
 Google Scholar
Google Scholar
[3] Fletcher D A, Geissler P L 2009 Annu. Rev. Phys. Chem. 60 469
 Google Scholar
Google Scholar
[4] Bechinger C, Di Leonardo R, Löwen H, Reichhardt C, Volpe G, Volpe G 2016 Rev. Mod. Phys. 88 045006
 Google Scholar
Google Scholar
[5] Paxton W F, Kistler K C, Olmeda C C, Sen A, St Angelo S K, Cao Y, Mallouk T E, Lammert P E, Crespi V H 2004 J. Am. Chem. Soc. 126 13424
 Google Scholar
Google Scholar
[6] Ramaswamy S 2010 Annu. Rev. Condens. Matter Phys. 1 323
 Google Scholar
Google Scholar
[7] Nelson B J, Kaliakatsos I K, Abbott J J 2010 Annu. Rev. Biomed. Eng. 12 55
 Google Scholar
Google Scholar
[8] Yang W, Misko V R, Nelissen K, Kong M, Peeters F M 2012 Soft Matter 8 5175
 Google Scholar
Google Scholar
[9] Patra D, Sengupta S, Duan W, Zhang H, Pavlick R, Sen A 2013 Nanoscale 5 1273
 Google Scholar
Google Scholar
[10] Vicsek T, Czirók A, Ben-Jacob E, Cohen I, Shochet O 1995 Phys. Rev. Lett. 75 1226
 Google Scholar
Google Scholar
[11] Grégoire G, Chaté H 2004 Phys. Rev. Lett. 92 025702
 Google Scholar
Google Scholar
[12] Peruani F, Deutsch A, Bär M 2006 Phys. Rev. E 74 030904
 Google Scholar
Google Scholar
[13] Aranson I S, Tsimring L S 2003 Phys. Rev. E 67 021305
 Google Scholar
Google Scholar
[14] Ginelli F, Peruani F, Bär M, Chaté H 2010 Phys. Rev. Lett. 104 184502
 Google Scholar
Google Scholar
[15] Caprini L, Marconi U M B 2021 Soft Matter 17 4109
 Google Scholar
Google Scholar
[16] Lushi E, Wioland H, Goldstein R E 2014 Proc. Natl. Acad. Sci. 111 9733
 Google Scholar
Google Scholar
[17] 何景熙, 秦超然, 许天亮, 陈康, 田文得 2022 71 150501
 Google Scholar
Google Scholar
He J X, Qin C R, Xu T L, Chen K, Tian W D 2022 Acta Phys. Sin. 71 150501
 Google Scholar
Google Scholar
[18] Wang J H, Xu T L, He J X, Chen K, Tian W D 2023 Chin. Phys. B 32 070501
 Google Scholar
Google Scholar
[19] Xu T L, Qin C R, Tang B, Gao J C, Zhou J, Chen K, Zhang T H, Tian W D 2024 J. Chem. Phys. 161 064905
 Google Scholar
Google Scholar
[20] Lam K D N T, Schindler M, Dauchot O 2015 New J. Phys. 17 113056
 Google Scholar
Google Scholar
[21] Giavazzi F, Paoluzzi M, Macchi M, Bi D, Scita G, Manning M L, Cerbino R, Marchetti M C 2018 Soft matter 14 3471
 Google Scholar
Google Scholar
[22] Caprini L, Marini Bettolo Marconi U, Puglisi A 2020 Phys. Rev. Lett. 124 078001
 Google Scholar
Google Scholar
[23] Caprini L, Marconi U M B, Maggi C, Paoluzzi M, Puglisi A 2020 Phys. Rev. Res. 2 023321
 Google Scholar
Google Scholar
[24] Kopp R A, Klapp S H 2023 Europhys. Lett. 143 17002
 Google Scholar
Google Scholar
[25] Caprini L, Löwen H 2023 Phys. Rev. Lett. 130 148202
 Google Scholar
Google Scholar
[26] Chakraborty S, Das S K 2020 J. Chem. Phys. 153 044905
 Google Scholar
Google Scholar
[27] Barberis L, Peruani F 2019 J. Chem. Phys. 150 144905
 Google Scholar
Google Scholar
[28] Hrishikesh B, Mani E 2023 Soft Matter 19 225
 Google Scholar
Google Scholar
[29] Hrishikesh B, Mani E 2022 Phys. Chem. Chem. Phys. 24 19792
 Google Scholar
Google Scholar
[30] Du Q, Faber V, Gunzburger M 1999 SIAM Rev. 41 637
 Google Scholar
Google Scholar
[31] Digregorio P, Levis D, Suma A, Cugliandolo L F, Gonnella G, Pagonabarraga I 2018 Phys. Rev. Lett. 121 098003
 Google Scholar
Google Scholar
[32] Ballerini M, Cabibbo N, Candelier R, Cavagna A, Cisbani E, Giardina I, Lecomte V, Orlandi A, Parisi G, Procaccini A, Viale M, Zdravkovic V 2008 Proc. Natl. Acad. Sci. 105 1232
 Google Scholar
Google Scholar
[33] Alert R, Trepat X 2020 Annu. Rev. Condens. Matter Phys. 11 77
 Google Scholar
Google Scholar
-
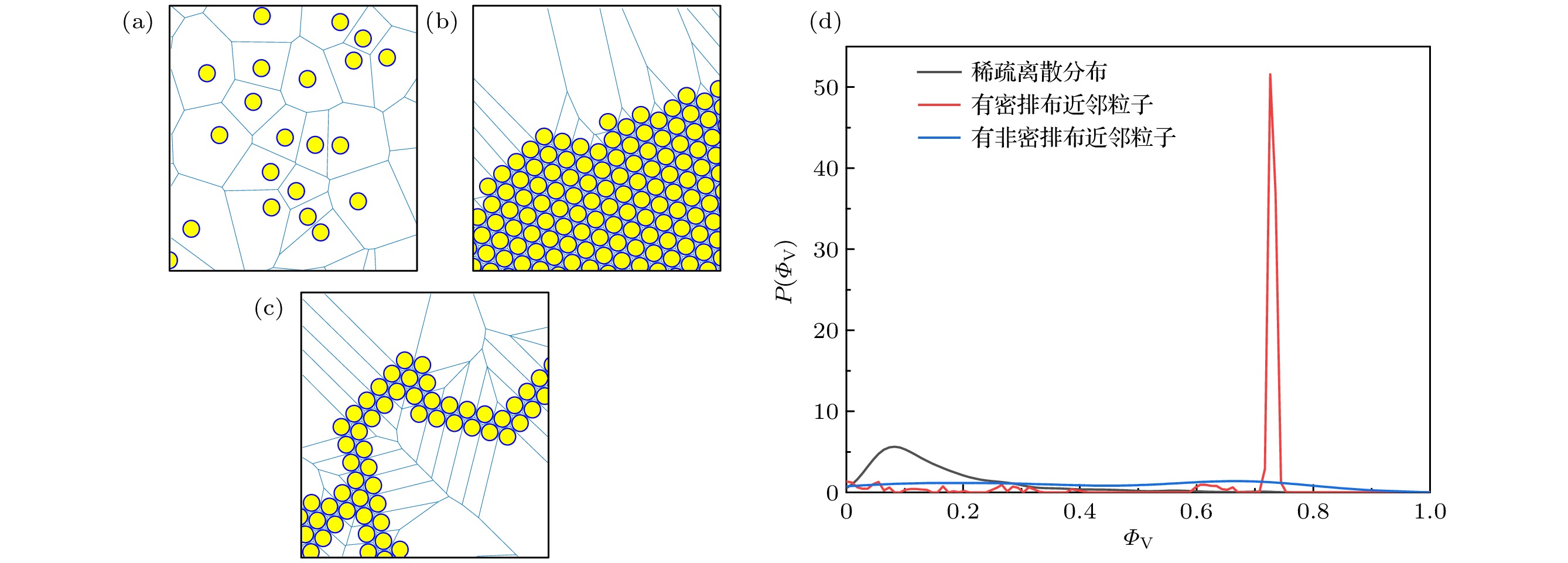
图 1 (a)稀疏离散分布的粒子; (b)有密排布近邻粒子的粒子; (c)有非密排布近邻粒子的粒子; (d)三种粒子分布下的概率分布函数$P({\varPhi _{\text{V}}})$图像, 其中黄色圆形表示粒子, 浅蓝色线表示粒子所在泰森多边形的边界
Fig. 1. (a) Particles in a sparse state; (b) particles with densely packed neighboring particles; (c) particles with non-densely packed neighboring particles; (d) the probability distribution function $P({\varPhi _{\text{V}}})$ under three particle distributions, the yellow circles indicate the particles, while the light blue lines represent the boundaries of Thiessen polygons.
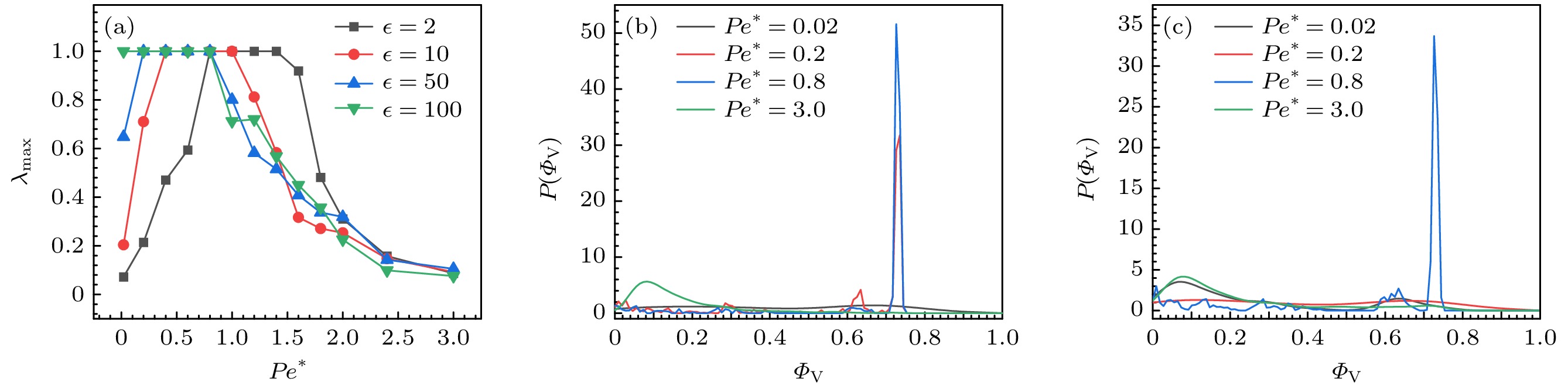
图 2 低填充分数($\phi = 0.1$)系统中, (a)不同$ \epsilon $下, 最大团簇分数${\lambda _{{\text{max}}}}$与约化佩克莱特数$P{e^*}$的关系; (b), (c) $ \epsilon=100 $和$ \epsilon=2 $的系统中, 不同$P{e^*}$下的概率分布函数$P({\varPhi _{\text{V}}})$
Fig. 2. In a low packing fraction system ($\phi = 0.1$), (a) the maximum cluster fraction ${\lambda _{{\text{max}}}}$ as a function of the reduced Peclet number $P{e^*}$ for different $ \epsilon $; (b), (c) the probability distribution function $P({\varPhi _{\text{V}}})$ for different $P{e^*}$ when $ \epsilon=100 $ and $ \epsilon=2 $, respectively.
图 3 低填充分数系统($\phi = 0.1$)的快照 (a)网状团簇结构, $P{e^*} = 0.02$, $ \epsilon=100 $; (b)块状团簇结构, $P{e^*} = 0.8$, $ \epsilon=100 $; (c)—(e)离散结构, 其中(c) $P{e^*} = 3.0$, $ \epsilon=100 $; (d) $P{e^*} = 0.02$, $ \epsilon=2 $; (e) $P{e^*} = 0.2$, $ \epsilon=2 $; 线条意义同图1
Fig. 3. Snapshots of systems with a low packing fraction ($\phi = 0.1$): (a) The network-like cluster structure, where $P{e^*} = 0.2$ and $ \epsilon=100 $; (b) the block-like cluster structure, where $P{e^*} = 0.8$ and $ \epsilon=100 $; (c)−(e) the discrete structure, where (c) $P{e^*} = 3.0$ and $ \epsilon=100 $; (d) $P{e^*} = 0.02$ and $ \epsilon=2 $; (e) $P{e^*} = 0.2$ and $ \epsilon=2 $. The line types are the same as those in Fig. 1.
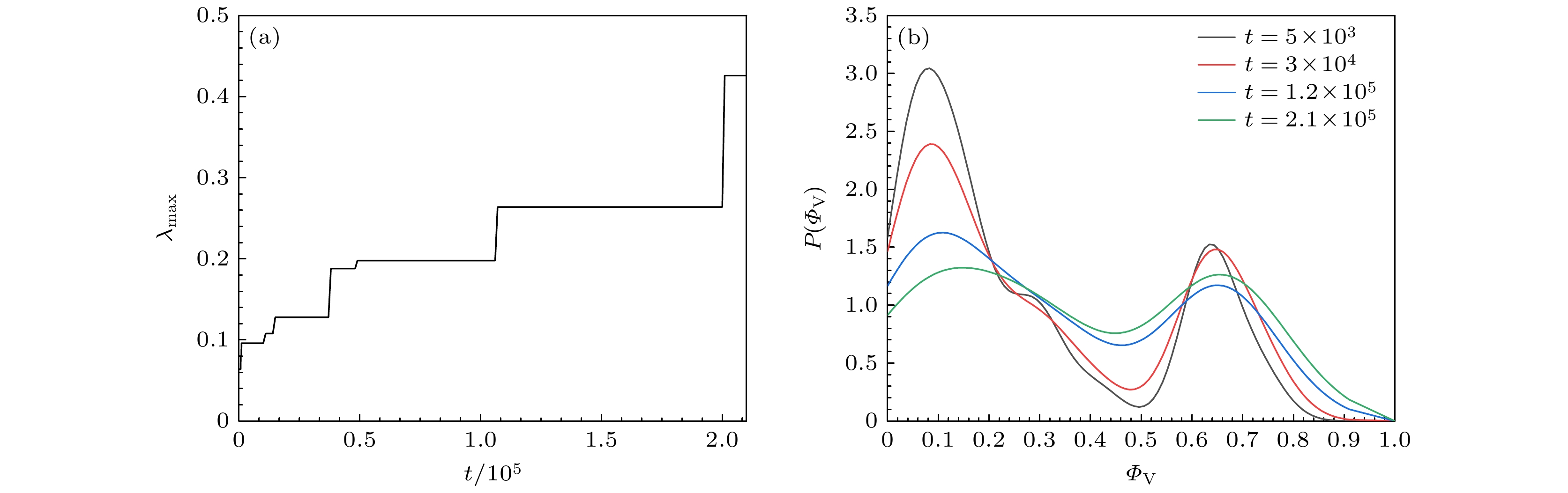
图 4 (a)最大团簇分数${\lambda _{{\text{max}}}}$随时间的变化; (b)不同时间下的概率分布函数$P({\varPhi _{\text{V}}})$; 其他参数分别为$\phi = 0.1$, $ \epsilon=2 $和$P{e^*} = 0.02$
Fig. 4. (a) Time evolution of the largest cluster fraction ${\lambda _{{\text{max}}}}$; (b) the probability distribution function $P({\varPhi _{\text{V}}})$ at different $t$. The other parameters are $\phi = 0.1$, $ \epsilon=2 $ and $P{e^*} = 0.02$, respectively.
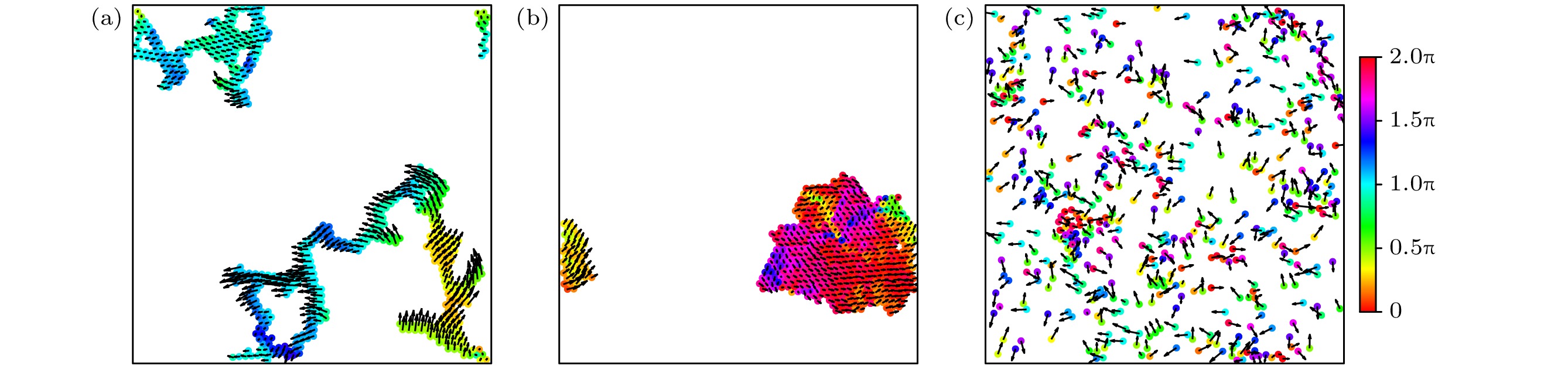
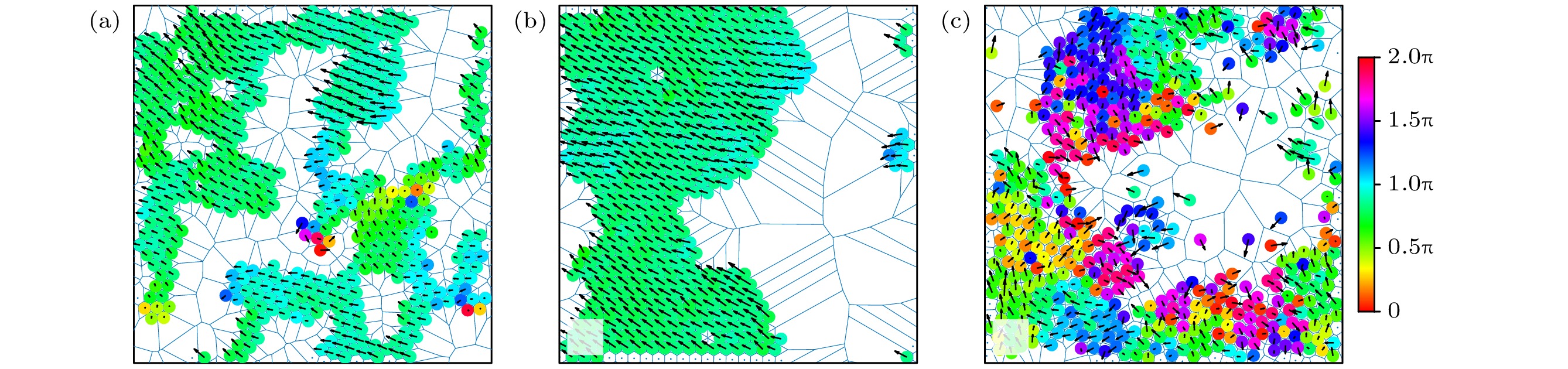
图 6 粒子的位置及速度的典型快照 (a) $P{e^*} = 0.02$; (b) $P{e^*} = 0.8$; (c) $P{e^*} = 3.0$; 其他参数分别为$\phi = 0.1$和$ \epsilon=100 $, 其中, 粒子颜色表示其速度方向与x轴正方形的夹角, 黑色箭头标注了粒子的速度大小和方向
Fig. 6. Typical snapshots of the position and velocity of particles: (a) $P{e^*} = 0.02$; (b) $P{e^*} = 0.8$; (c) $P{e^*} = 3.0$. The other parameters are $\phi = 0.1$ and $ \epsilon=100 $. The color of the particles represents the angle between their velocity direction and the positive x-axis, with black arrows indicating the magnitude and direction of each particle’s velocity.
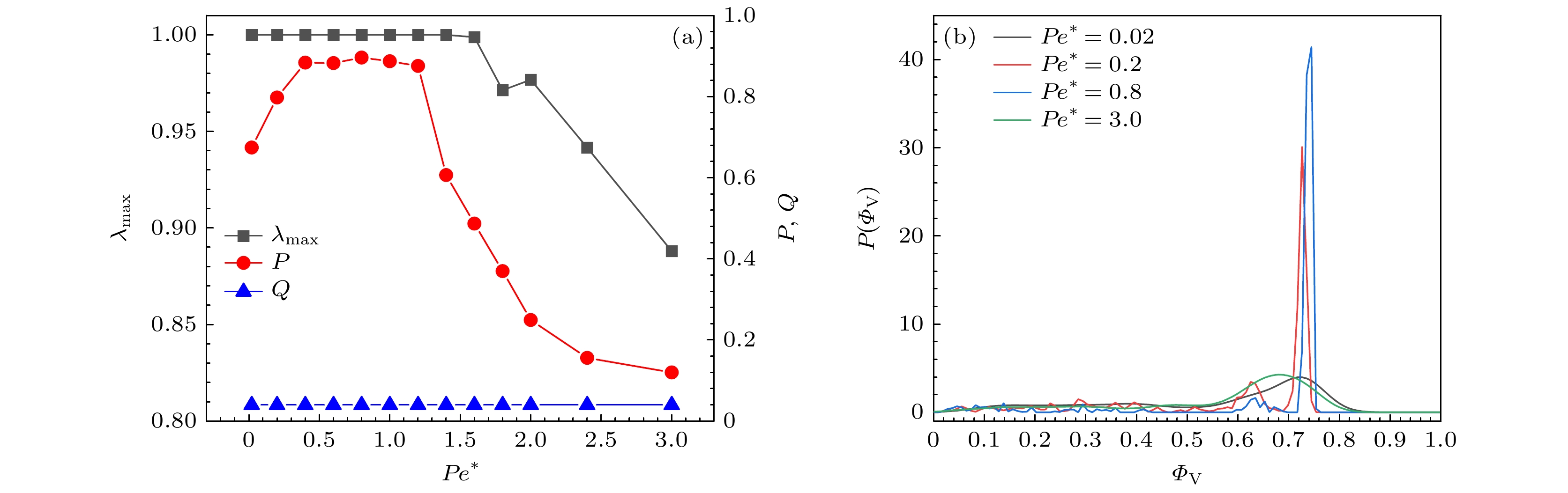
图 7 (a) 最大团簇分数${\lambda _{{\text{max}}}}$、全局速度对齐序参量$P$和极性平均参量$Q$随$P{e^*}$的变化; (b) 不同$P{e^*}$下的概率分布函数$P({\varPhi _{\text{V}}})$; 其他参数分别为$\phi = 0.4$和$ \epsilon=100 $
Fig. 7. (a) Variation of the largest cluster fraction ${\lambda _{{\text{max}}}}$, the global velocity alignment order $P$ and the polarity averaged order parameter $Q$ with $P{e^*}$; (b) the probability distribution function $P({\varPhi _{\text{V}}})$ for different $P{e^*}$. The other parameters are $\phi = 0.4$ and $ \epsilon=100 $.
图 8 粒子的位置及速度的典型快照 (a) $P{e^*} = 0.02$; (b) $P{e^*} = 0.8$; (c) $P{e^*} = 3.0$; 其他参数分别为$\phi = 0.4$和$ \epsilon=100 $, 其中, 粒子的颜色表示其速度方向与x轴正方形的夹角, 黑色箭头标注了每个粒子的速度大小和方向, 浅蓝色线表示粒子所在泰森多边形的边界
Fig. 8. Typical snapshots of the position and velocity of particles: (a) $P{e^*} = 0.02$; (b) $P{e^*} = 0.8$; (c) $P{e^*} = 3.0$. The other parameters are $\phi = 0.4$ and $ \epsilon=100 $. The color of the particles indicates the angle between their velocity and the positive x-axis, with black arrows showing the magnitude and direction of particles’ velocity, and light blue lines representing the boundaries of the Thiessen polygons.
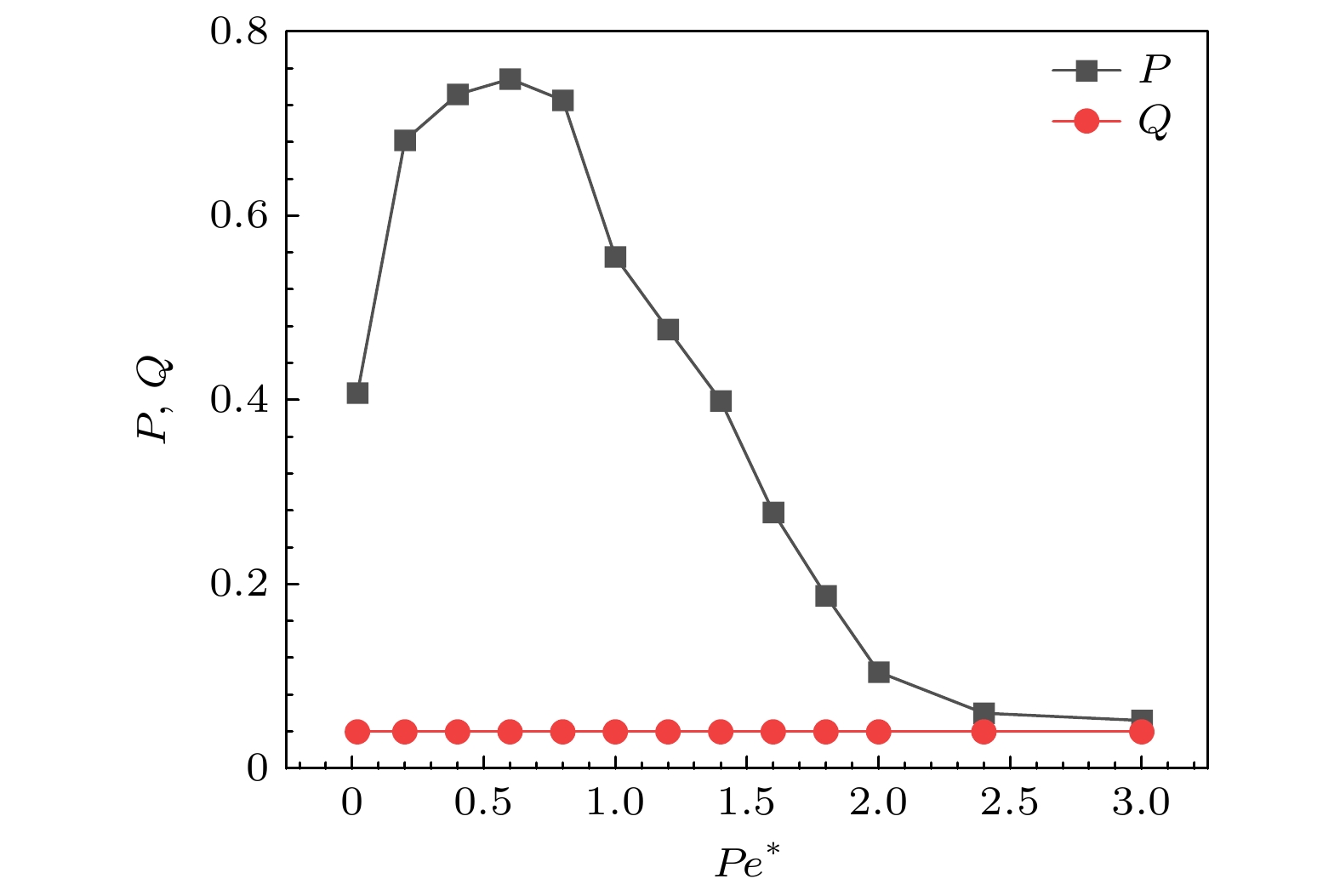
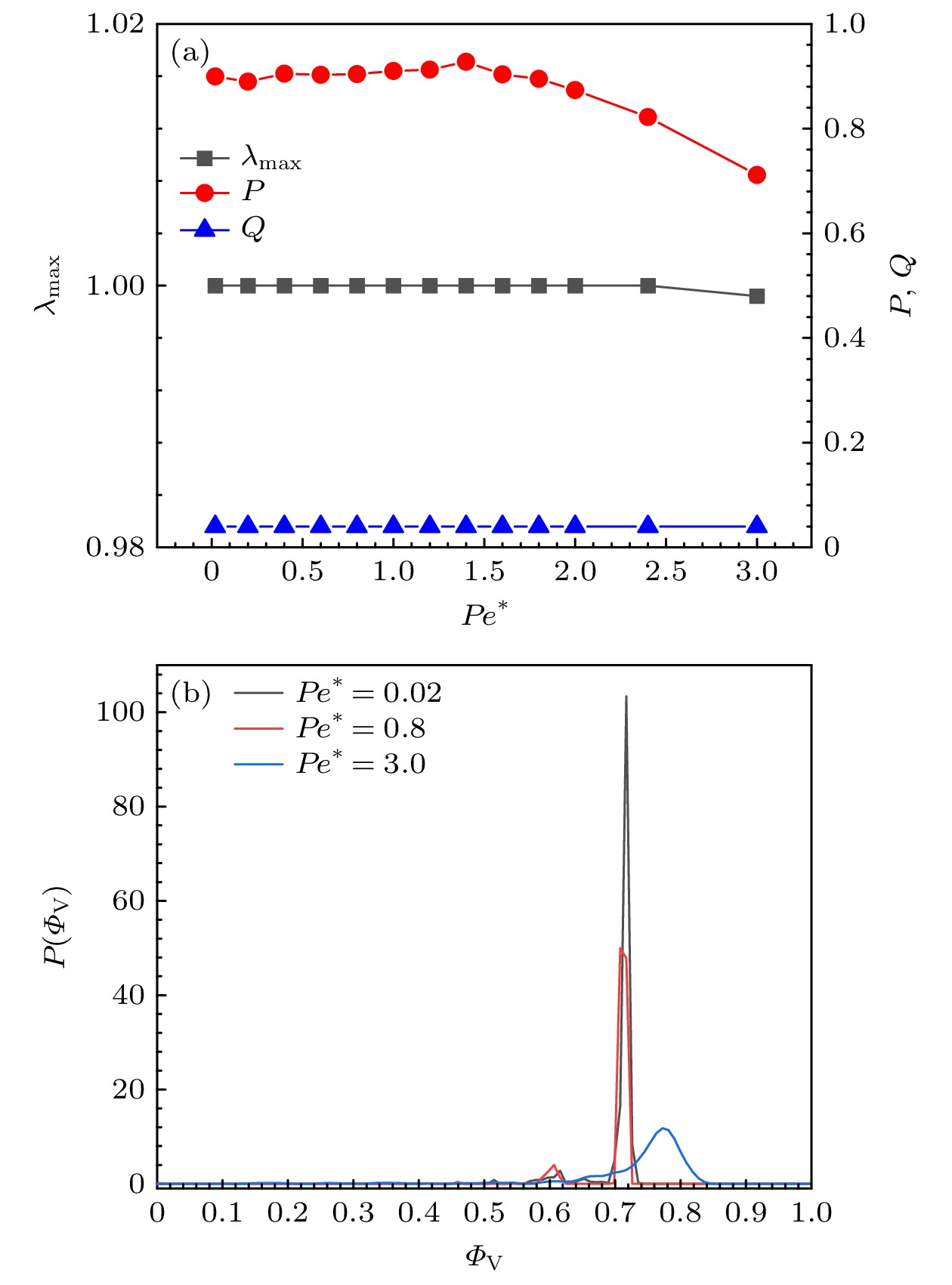
图 9 (a)最大团簇分数${\lambda _{{\text{max}}}}$、全局速度对齐序参量$P$和极性平均参量$Q$随$P{e^*}$的变化; (b)不同$P{e^*}$下, 概率分布函数$P({\varPhi _{\text{V}}})$的图像; 其他参数分别为$\phi = 0.7$和$ \epsilon=100 $
Fig. 9. (a) Variation of the largest cluster fraction ${\lambda _{{\text{max}}}}$, the global velocity alignment order $P$ and the polarity averaged order parameter $Q$ with $P{e^*}$; (b) the probability distribution function $P({\varPhi _{\text{V}}})$ for different $P{e^*}$. The other parameters are $\phi = 0.7$ and $ \epsilon=100 $.
-
[1] Emlen J T 1952 The Auk 69 160
 Google Scholar
Google Scholar
[2] Becco C, Vandewalle N, Delcourt J, Poncin P 2006 Phys. A 367 487
 Google Scholar
Google Scholar
[3] Fletcher D A, Geissler P L 2009 Annu. Rev. Phys. Chem. 60 469
 Google Scholar
Google Scholar
[4] Bechinger C, Di Leonardo R, Löwen H, Reichhardt C, Volpe G, Volpe G 2016 Rev. Mod. Phys. 88 045006
 Google Scholar
Google Scholar
[5] Paxton W F, Kistler K C, Olmeda C C, Sen A, St Angelo S K, Cao Y, Mallouk T E, Lammert P E, Crespi V H 2004 J. Am. Chem. Soc. 126 13424
 Google Scholar
Google Scholar
[6] Ramaswamy S 2010 Annu. Rev. Condens. Matter Phys. 1 323
 Google Scholar
Google Scholar
[7] Nelson B J, Kaliakatsos I K, Abbott J J 2010 Annu. Rev. Biomed. Eng. 12 55
 Google Scholar
Google Scholar
[8] Yang W, Misko V R, Nelissen K, Kong M, Peeters F M 2012 Soft Matter 8 5175
 Google Scholar
Google Scholar
[9] Patra D, Sengupta S, Duan W, Zhang H, Pavlick R, Sen A 2013 Nanoscale 5 1273
 Google Scholar
Google Scholar
[10] Vicsek T, Czirók A, Ben-Jacob E, Cohen I, Shochet O 1995 Phys. Rev. Lett. 75 1226
 Google Scholar
Google Scholar
[11] Grégoire G, Chaté H 2004 Phys. Rev. Lett. 92 025702
 Google Scholar
Google Scholar
[12] Peruani F, Deutsch A, Bär M 2006 Phys. Rev. E 74 030904
 Google Scholar
Google Scholar
[13] Aranson I S, Tsimring L S 2003 Phys. Rev. E 67 021305
 Google Scholar
Google Scholar
[14] Ginelli F, Peruani F, Bär M, Chaté H 2010 Phys. Rev. Lett. 104 184502
 Google Scholar
Google Scholar
[15] Caprini L, Marconi U M B 2021 Soft Matter 17 4109
 Google Scholar
Google Scholar
[16] Lushi E, Wioland H, Goldstein R E 2014 Proc. Natl. Acad. Sci. 111 9733
 Google Scholar
Google Scholar
[17] 何景熙, 秦超然, 许天亮, 陈康, 田文得 2022 71 150501
 Google Scholar
Google Scholar
He J X, Qin C R, Xu T L, Chen K, Tian W D 2022 Acta Phys. Sin. 71 150501
 Google Scholar
Google Scholar
[18] Wang J H, Xu T L, He J X, Chen K, Tian W D 2023 Chin. Phys. B 32 070501
 Google Scholar
Google Scholar
[19] Xu T L, Qin C R, Tang B, Gao J C, Zhou J, Chen K, Zhang T H, Tian W D 2024 J. Chem. Phys. 161 064905
 Google Scholar
Google Scholar
[20] Lam K D N T, Schindler M, Dauchot O 2015 New J. Phys. 17 113056
 Google Scholar
Google Scholar
[21] Giavazzi F, Paoluzzi M, Macchi M, Bi D, Scita G, Manning M L, Cerbino R, Marchetti M C 2018 Soft matter 14 3471
 Google Scholar
Google Scholar
[22] Caprini L, Marini Bettolo Marconi U, Puglisi A 2020 Phys. Rev. Lett. 124 078001
 Google Scholar
Google Scholar
[23] Caprini L, Marconi U M B, Maggi C, Paoluzzi M, Puglisi A 2020 Phys. Rev. Res. 2 023321
 Google Scholar
Google Scholar
[24] Kopp R A, Klapp S H 2023 Europhys. Lett. 143 17002
 Google Scholar
Google Scholar
[25] Caprini L, Löwen H 2023 Phys. Rev. Lett. 130 148202
 Google Scholar
Google Scholar
[26] Chakraborty S, Das S K 2020 J. Chem. Phys. 153 044905
 Google Scholar
Google Scholar
[27] Barberis L, Peruani F 2019 J. Chem. Phys. 150 144905
 Google Scholar
Google Scholar
[28] Hrishikesh B, Mani E 2023 Soft Matter 19 225
 Google Scholar
Google Scholar
[29] Hrishikesh B, Mani E 2022 Phys. Chem. Chem. Phys. 24 19792
 Google Scholar
Google Scholar
[30] Du Q, Faber V, Gunzburger M 1999 SIAM Rev. 41 637
 Google Scholar
Google Scholar
[31] Digregorio P, Levis D, Suma A, Cugliandolo L F, Gonnella G, Pagonabarraga I 2018 Phys. Rev. Lett. 121 098003
 Google Scholar
Google Scholar
[32] Ballerini M, Cabibbo N, Candelier R, Cavagna A, Cisbani E, Giardina I, Lecomte V, Orlandi A, Parisi G, Procaccini A, Viale M, Zdravkovic V 2008 Proc. Natl. Acad. Sci. 105 1232
 Google Scholar
Google Scholar
[33] Alert R, Trepat X 2020 Annu. Rev. Condens. Matter Phys. 11 77
 Google Scholar
Google Scholar
计量
- 文章访问数: 3075
- PDF下载量: 112
- 被引次数: 0













 下载:
下载: