Scattering effect of very low frequency transmitter signals on energetic electrons in Earth’s inner belt and slot region

Liu Yang-Xi-Zi; Xiang Zheng; Guo Jian-Guang; Gu Xu-Dong; Fu Song; Zhou Ruo-Xian; Hua Man; Zhu Qi; Yi Juan; Ni Bin-Bin

doi:10.7498/aps.70.20202029

Abstract

Whistler mode very low frequency (VLF) waves from man-made ground-based transmitters in a frequency range of 10–30 kHz are mainly used for submarine communication, and they propagate primarily in the Earth-lower ionosphere waveguide and part of their energy can leak into the inner magnetosphere, leading the energetic electrons in inner radiation belt and slot region to precipitate into atmosphere and then affect the energetic electron dynamics in the near-Earth space. The scattering effects of artificial VLF signals from NWC, NAA and DHO38 transmitters on energetic electrons in Earth’s inner belt and slot region are investigated in detail in this work. Based on the quasi-linear theory and the Full Diffusion Code, we calculate the bounce-average pitch angle diffusion coefficients induced by NWC, NAA and DHO38 VLF transmitter signals, for which the resonance harmonics |N| ≤ 10 are considered, respectively. We further implement the one-dimensional Fokker-Planck diffusion simulations by using the available pitch angle diffusion rates to model the dynamic evolutions of energetic electrons caused by the scattering of the VLF transmitter signals in the inner belt and slot region in 200 d. The simulation results indicate that the NWC VLF transmitter signals are dominant in scattering ~100 keV electrons with pitch angles less than 60° at L ≤ 1.8, and the mainly scattered electron energy values increase with L-shell decreasing , from L = 1.8 to L = 1.5, the mainly scattered electron energy increases from 90–120 keV to 550–650 keV. The NAA and DHO38 VLF transmitter signals are important in scattering < 20 keV electrons with pitch angles less than 70° at higher L-shells (2.2 ≤ L ≤ 2.7), from L = 2.2 to L = 2.7, the mainly scattered electron energy decreases from 10–20 keV to several keV. The VLF transmitter signals are found to have a slight influence on the loss of energetic electrons with pitch angles larger than 80°.

Keywords:

Authors and contacts

1.
Department of Space Physics, School of Electronic Information, Wuhan University, Wuhan 430072, China
2.
Key Laboratory of Space Weather, National Center for Space Weather, China Meteorological Administration, Beijing 100081, China
3.
Center for Excellence in Comparative Planetology, Chinese Academy of Sciences, Hefei 230026, China

Corresponding author: Xiang Zheng, xiangzheng@whu.edu.cn ; Guo Jian-Guang, guojg@cma.gov.cn ;

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 42025404, 41704162, 41974186, 41674163, 41904144, 41904143), the B-type Strategic Priority Program of the Chinese Academy of Sciences (Grant No. XDB41000000), the Pre-research Projects on Civil Aerospace Technologies funded by the China National Space Administration (Grant Nos. D020303, D020308, D020104), and the China Postdoctoral Science Foundation (Grant No. 2019M662700)

FullText HTML : translate this paragraph

References

[1]	Xiang Z, Tu W, Li X, Ni B, Morley S K, Baker D N 2017 J. Geophys. Res. Space Phys. 122 9858 Google Scholar
[2]	Xiang Z, Tu W, Ni B, Henderson M G, Cao X 2018 Geophys. Res. Lett. 45 8035 Google Scholar
[3]	Ma X, Xiang Z, Ni B, Fu S, Cao X, Hua M, Guo D, Guo Y, Gu X, Liu Z, Zhu Q 2020 Earth Planet. Phys. 4 598 Google Scholar
[4]	Rosen A, Sanders N L 1971 J. Geophys. Res. 76 110 Google Scholar
[5]	Selesnick R S 2015 J. Geophys. Res. Space Phys. 120 2912 Google Scholar
[6]	Xiang Z, Li X, Selesnick R, Temerin M A, Ni B, Zhao H, Zhang K, Khoo L Y 2019 Geophys. Res. Lett. 46 1919 Google Scholar
[7]	Xiang Z, Li X, Temerin M A, Ni B, Zhao H, Zhang K, Khoo L Y 2020 J. Geophys. Res. Space Phys. 125 e2019JA027678
[8]	Xiang Z, Li X, Ni B, Temerin M A, Zhao H, Zhang K, Khoo L Y 2020 J. Geophys. Res. Space Phys. 125 e2020JA028042
[9]	Zhang K, Li X, Zhao H, Schiller Q, Khoo L Y, Xiang Z, Selesnick R, Temerin M A, Sauvaud J A 2019 Geophys. Res. Lett. 46 544 Google Scholar
[10]	Ni B, Hua M, Zhou R, Yi J, Fu S 2017 Geophys. Res. Lett. 44 3465 Google Scholar
[11]	Hua M, Ni B, Fu S, Gu X, Xiang Z, Cao X, Zhang W, He Y, Huang H, Lou Y, Zhang Y 2018 Geophys. Res. Lett. 45 10057 Google Scholar
[12]	Rodger C J, Clilverd M A, McCormick R J 2003 J. Geophys. Res. 108 1462 Google Scholar
[13]	Clilverd M A, Rodger C J, Nunn D 2004 J. Geophys. Res. A 109 12208 Google Scholar
[14]	Green A, Li W, Ma Q, Shen X C, Bortnik J, Hospodarsky G B 2020 Geophys. Res. Lett. 47 e2020GL089584
[15]	Ma Q, Li W, Thorne R M, Bortnik J, Kletzing C A, Kurth W S, Hospodarsky G B 2016 J. Geophys. Res. Space Phys. 121 274 Google Scholar
[16]	顾旭东, 何颖, 倪彬彬, 付松, 花漫, 项正 2020 地球 63 2121 Google Scholar Gu X D, He Y, Ni B B, Fu S, Hua M, Xiang Z 2020 Chin. J. Geophys. 63 2121 Google Scholar
[17]	Ni B, Yan L, Fu S, Gu X, Cao X, Xiang Z, Zhang Y 2020 Geophys. Res. Lett. 47 e2019GL086487
[18]	Ma Q, Mourenas D, Li W, Artemyev A, Thorne R M 2017 Geophys. Res. Lett. 44 6483 Google Scholar
[19]	Ross J P J, Meredith N P, Glauert S A, Horne R B, Clilverd M A 2019 J. Geophys. Res. Space Phys. 124 5260 Google Scholar
[20]	Hua M, Li W, Ni B, Ma Q, Green A, Shen X, Claudepierre S G, Bortnik J, Gu X, Fu S, Xiang Z, Reeves G D 2020 Nat. Commun. 11 4847 Google Scholar
[21]	Chen Y P, Yang G B, Ni B B, Zhao Z Y, Gu X D, Zhou C, Wang F 2016 Adv. Space Res. 57 1871 Google Scholar
[22]	Chen Y, Ni B, Gu X, Zhao Z, Yang G, Zhou C, Zhang Y 2017 Sci. Chin. Technol. Sci. 60 166 Google Scholar
[23]	易娟, 顾旭东, 李志鹏, 林仁桐, 蔡毅徽, 陈隆, 倪彬彬, 乐新安 2019 地球 62 3223 Google Scholar Yi J, Gu X D, Li Z P, Lin R T, Cai Y H, Chen L, Ni B B, Yue X A 2019 Chin. J. Geophys. 62 3223 Google Scholar
[24]	Yi J, Gu X, Cheng W, Tang X, Chen L, Ni B, Zhou R, Zhao Z, Wang Q, Zhou L 2020 Earth Planet. Phys. 4 238 Google Scholar
[25]	Zhou R, Gu X, Yang K, Li G, Ni B, Yi J, Chen L, Zhao F, Zhao Z, Wang Q, Zhou L 2020 Earth Planet. Phys. 4 120 Google Scholar
[26]	Vampola A L, Kuck G A 1978 J. Geophys. Res. 83 2543 Google Scholar
[27]	Koons H C, Edgar B C, Vampola A L 1981 J. Geophys. Res. 86 640 Google Scholar
[28]	Abel B, Thorne R M 1998 J. Geophys. Res. 103 2397 Google Scholar
[29]	Gamble R J, Rodger C J, Clilverd M A, Sauvaud J A, Thomson N R, Stewart S L, McCormick R J, Parrot M, Berthelier J J 2008 J. Geophys. Res. A 113 10211 Google Scholar
[30]	Graf K L, Inan U S, Piddyachiy D, Kulkarni P, Parrot M, Sauvaud J A 2009 J. Geophys. Res. A 114 07205 Google Scholar
[31]	Selesnick R S, Albert J M, Starks M J 2013 J. Geophys. Res. Space Phys. 118 628 Google Scholar
[32]	Agapitov O V, Artemyev A V, Mourenas D, Kasahara Y, Krasnoselskikh V 2014 J. Geophys. Res. Space Phys. 119 2876 Google Scholar
[33]	Claudepierre S G, Ma Q, Bortnik J, O'Brien T P, Fennell J F, Blake J B 2020 Geophys. Res. Lett. 47 e2019GL086056 Google Scholar
[34]	Imhof W L, Reagan J B, Voss H D, Gaines E E, Datlowe D W, Mobilia J, Helliwell R A, Inan U S, Katsufrakis J, Joiner R G 1983 Geophys. Res. Lett. 10 361 Google Scholar
[35]	Inan U S, Chang H C, Helliwell R A, Imhof W L, Reagan J B, Walt M 1985 J. Geophys. Res. 90 359 Google Scholar
[36]	王平, 王焕玉, 马宇蒨, 李新乔, 卢红, 孟祥承, 张吉龙, 王辉, 石峰, 徐岩冰, 于晓霞, 赵小芸, 吴峰 2011 60 039401 Google Scholar Wang P, Wang H Y, Ma Y Q, Li X Q, Lu H, Meng X C, Zhang J L, Wang H, Shi F, Xu Y B, Yu X X, Zhao X Y, Wu F 2011 Acta Phys. Sin. 60 039401 Google Scholar
[37]	Sauvaud J A, Maggiolo R, Jacquey C, Parrot M, Berthelier J J, Gamble R J, Rodger C J 2008 Geophys. Res. Lett. 35 L09101 Google Scholar
[38]	Clilverd M A, Rodger C J, Gamble R, Meredith N P, Parrot M, Berthelier J J, Thomson N R 2008 J. Geophys. Res. A 113 04211 Google Scholar
[39]	Kulkarni P, Inan U S, Bell T F, Bortnik J 2008 J. Geophys. Res. A 113 07214 Google Scholar
[40]	张振霞, 王辰宇, 李强, 吴书贵 2014 63 079401 Google Scholar Zhang Z X, Wang C Y, Li Q, Wu S G 2014 Acta Phys. Sin. 63 079401 Google Scholar
[41]	罗旭东, 牛胜利, 左应红 2015 64 069401 Google Scholar Luo X D, Niu S L, Zuo Y H 2015 Acta Phys. Sin. 64 069401 Google Scholar
[42]	Meredith N P, Horne R B, Clilverd M A, Ross J P J 2019 J. Geophys. Res. Space Phys. 124 5246 Google Scholar
[43]	Ozhogin P, Tu J, Song P, Reinisch B W 2012 J. Geophys. Res. A 117 06225 Google Scholar
[44]	Ni B, Thorne R M, Meredith N P, Shprits Y Y, Horne R B 2011 J. Geophys. Res. A 116 10207 Google Scholar
[45]	Ni B, Thorne R M, Shprits Y Y, Bortnik J 2008 Geophys. Res. Lett. 35 L11106 Google Scholar
[46]	Ma Q, Artemyev A V, Mourenas D, Li W, Thorne R M, Kletzing C A, Kurth W S, Hospodarsky G B, Reeves G D, Spence H E, Wygant J 2017 Geophys. Res. Lett. 44 12057
[47]	Xiao F, Su Z, Zheng H, Wang S 2009 J. Geophys. Res. A 114 03201 Google Scholar
[48]	Xiao F, Shen C, Wang Y, Zheng H, Wang S 2008 J. Geophys. Res. A 113 05203 Google Scholar

Cited By

图 1 计算得到的三个台站的波幅

Figure 1. Calculated wave amplitudes from three VLF transmitters.

DownLoad: Full-Size Img PowerPoint

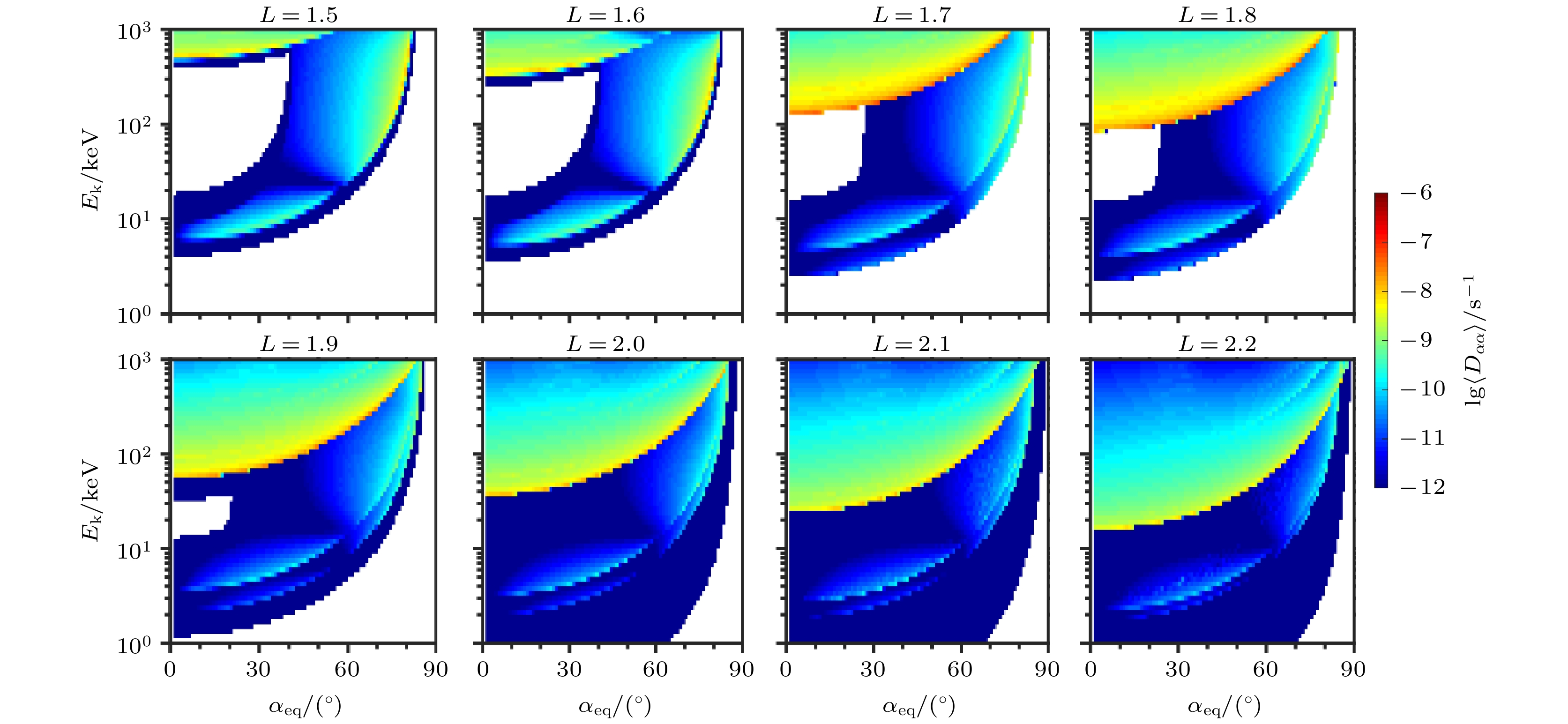
图 2 NWC台站信号在L = 1.5—2.2导致的电子弹跳平均投掷角扩散系数$\left\langle {{D_{\alpha \alpha }}} \right\rangle $. 图中横坐标为赤道投掷角${\alpha _{{\rm{eq}}}}$, 纵坐标为电子能量${E_{\rm{k}}}$, 颜色表示扩散系数的大小

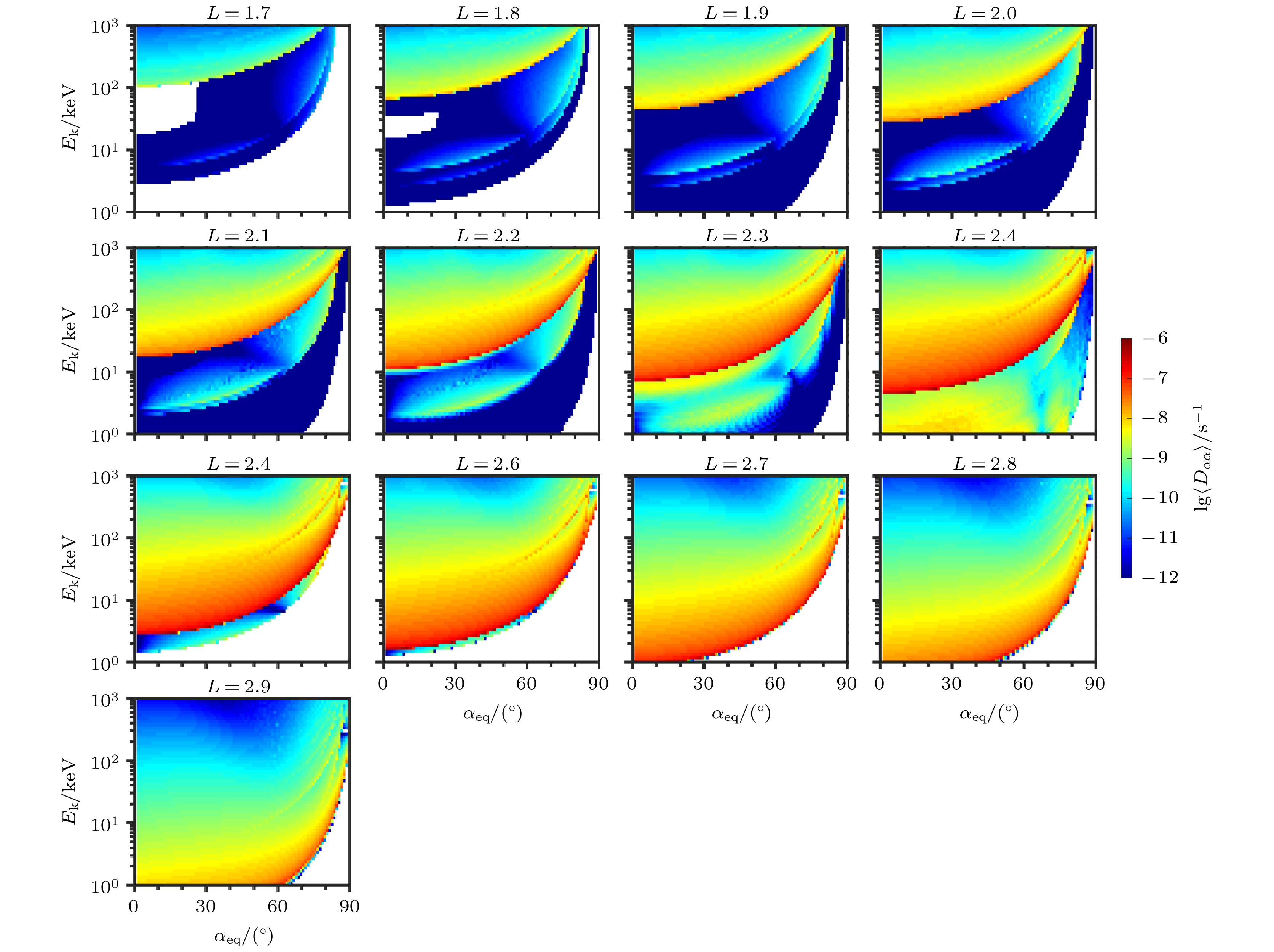
Figure 2. The color-code bounce-averaged pitch angle diffusion coefficients $\left\langle {{D_{\alpha \alpha }}} \right\rangle $ as a function of equatorial pitch angle ${\alpha _{{\rm{eq}}}}$ and electron kinetic energy ${E_{\rm{k}}}$ induced by VLF transmitter signals from NWC at L = 1.5–2.2.

DownLoad: Full-Size Img PowerPoint

图 3 NAA台站信号在L = 1.7—3.0导致的电子弹跳平均投掷角扩散系数. 格式同图2

Figure 3. Same as in Fig. 2 except for VLF transmitter signals from NAA at L = 1.7–3.0.

DownLoad: Full-Size Img PowerPoint

图 4 DHO38台站信号在L = 1.7−2.9导致的电子弹跳平均投掷角扩散系数. 格式同图2

Figure 4. Same as in figure 2 except for VLF transmitter signals from DHO38 at L = 1.7−2.9.

DownLoad: Full-Size Img PowerPoint

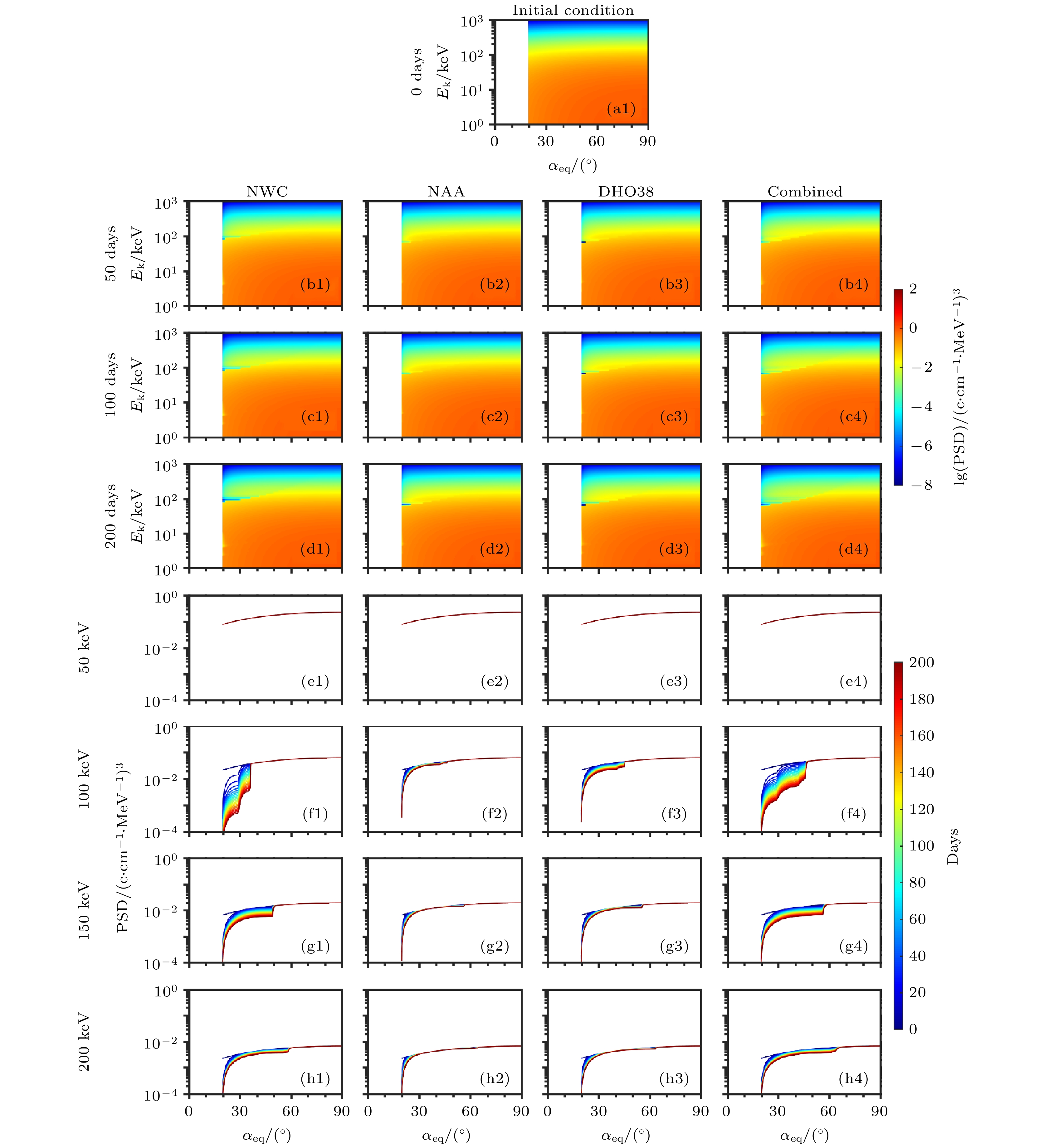
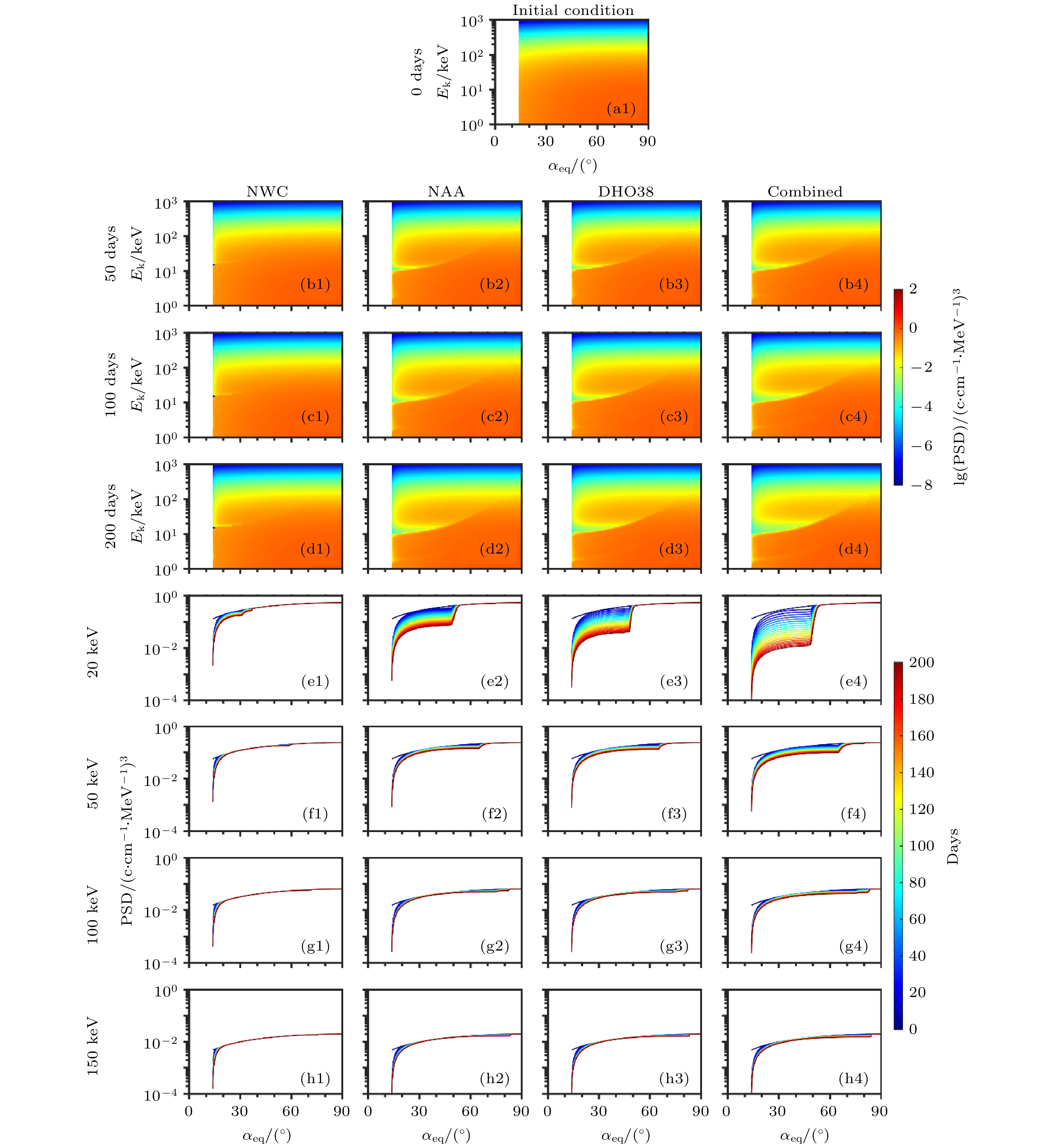
图 5 在L = 1.8处, 不同VLF台站信号对电子散射效果的模拟, 从左至右分别为NWC, NAA, DHO38台站信号单独散射和三个台站信号联合散射　(a1)−(d4)不同模拟时间的电子相空间密度分布二维图, 颜色表示电子相空间密度的大小; (e1)−(h4)指定能级电子的相空间密度随时间演化的过程图, 线条颜色表示不同的时间

Figure 5. (a1)−(d4) Two dimensional distributions of color-code electron phase space density (PSD) as a function of equatorial pitch angle ${\alpha _{{\rm{eq}}}}$ and electron kinetic energy ${E_{\rm{k}}}$ at the indicated interaction time stamps at L = 1.8 induced by different VLF transmitter signals (from left to right): NWC, NAA, DHO38 individual scattering and combined scattering; (e1)−(h4) temporal evolution of electron PSD distribution as a function of ${\alpha _{{\rm{eq}}}}$ for the indicated four electron energies at the color-coded interaction time stamps.

DownLoad: Full-Size Img PowerPoint

图 6 在L = 2.2处, 不同VLF台站信号对电子的散射效果模拟, 格式同图5

Figure 6. Same as in Fig. 5 except for at L = 2.2.

DownLoad: Full-Size Img PowerPoint

图 7 在L = 2.6处, 不同VLF台站信号对电子的散射效果模拟. 格式同图5

Figure 7. Same as in Fig. 5 except for at L = 2.6.

DownLoad: Full-Size Img PowerPoint

表 1 选取计算的台站信息

Table 1. The information of the three selected VLF transmitters.

台站频率/kHz 功率/kW 经纬度 L-shell 磁层中波
幅范围/L

NWC 19.8 1000 21.8°S
114.2°E 1.42 1.5—2.2
NAA 24.0 1000 44.6°N
67.3°W 2.74 1.7—3.0
DHO38 23.4 300 53.1°N
7.6°E 2.38 1.7—2.9

DownLoad: CSV

map

[1]	Xiang Z, Tu W, Li X, Ni B, Morley S K, Baker D N 2017 J. Geophys. Res. Space Phys. 122 9858 Google Scholar
[2]	Xiang Z, Tu W, Ni B, Henderson M G, Cao X 2018 Geophys. Res. Lett. 45 8035 Google Scholar
[3]	Ma X, Xiang Z, Ni B, Fu S, Cao X, Hua M, Guo D, Guo Y, Gu X, Liu Z, Zhu Q 2020 Earth Planet. Phys. 4 598 Google Scholar
[4]	Rosen A, Sanders N L 1971 J. Geophys. Res. 76 110 Google Scholar
[5]	Selesnick R S 2015 J. Geophys. Res. Space Phys. 120 2912 Google Scholar
[6]	Xiang Z, Li X, Selesnick R, Temerin M A, Ni B, Zhao H, Zhang K, Khoo L Y 2019 Geophys. Res. Lett. 46 1919 Google Scholar
[7]	Xiang Z, Li X, Temerin M A, Ni B, Zhao H, Zhang K, Khoo L Y 2020 J. Geophys. Res. Space Phys. 125 e2019JA027678
[8]	Xiang Z, Li X, Ni B, Temerin M A, Zhao H, Zhang K, Khoo L Y 2020 J. Geophys. Res. Space Phys. 125 e2020JA028042
[9]	Zhang K, Li X, Zhao H, Schiller Q, Khoo L Y, Xiang Z, Selesnick R, Temerin M A, Sauvaud J A 2019 Geophys. Res. Lett. 46 544 Google Scholar
[10]	Ni B, Hua M, Zhou R, Yi J, Fu S 2017 Geophys. Res. Lett. 44 3465 Google Scholar
[11]	Hua M, Ni B, Fu S, Gu X, Xiang Z, Cao X, Zhang W, He Y, Huang H, Lou Y, Zhang Y 2018 Geophys. Res. Lett. 45 10057 Google Scholar
[12]	Rodger C J, Clilverd M A, McCormick R J 2003 J. Geophys. Res. 108 1462 Google Scholar
[13]	Clilverd M A, Rodger C J, Nunn D 2004 J. Geophys. Res. A 109 12208 Google Scholar
[14]	Green A, Li W, Ma Q, Shen X C, Bortnik J, Hospodarsky G B 2020 Geophys. Res. Lett. 47 e2020GL089584
[15]	Ma Q, Li W, Thorne R M, Bortnik J, Kletzing C A, Kurth W S, Hospodarsky G B 2016 J. Geophys. Res. Space Phys. 121 274 Google Scholar
[16]	顾旭东, 何颖, 倪彬彬, 付松, 花漫, 项正 2020 地球 63 2121 Google Scholar Gu X D, He Y, Ni B B, Fu S, Hua M, Xiang Z 2020 Chin. J. Geophys. 63 2121 Google Scholar
[17]	Ni B, Yan L, Fu S, Gu X, Cao X, Xiang Z, Zhang Y 2020 Geophys. Res. Lett. 47 e2019GL086487
[18]	Ma Q, Mourenas D, Li W, Artemyev A, Thorne R M 2017 Geophys. Res. Lett. 44 6483 Google Scholar
[19]	Ross J P J, Meredith N P, Glauert S A, Horne R B, Clilverd M A 2019 J. Geophys. Res. Space Phys. 124 5260 Google Scholar
[20]	Hua M, Li W, Ni B, Ma Q, Green A, Shen X, Claudepierre S G, Bortnik J, Gu X, Fu S, Xiang Z, Reeves G D 2020 Nat. Commun. 11 4847 Google Scholar
[21]	Chen Y P, Yang G B, Ni B B, Zhao Z Y, Gu X D, Zhou C, Wang F 2016 Adv. Space Res. 57 1871 Google Scholar
[22]	Chen Y, Ni B, Gu X, Zhao Z, Yang G, Zhou C, Zhang Y 2017 Sci. Chin. Technol. Sci. 60 166 Google Scholar
[23]	易娟, 顾旭东, 李志鹏, 林仁桐, 蔡毅徽, 陈隆, 倪彬彬, 乐新安 2019 地球 62 3223 Google Scholar Yi J, Gu X D, Li Z P, Lin R T, Cai Y H, Chen L, Ni B B, Yue X A 2019 Chin. J. Geophys. 62 3223 Google Scholar
[24]	Yi J, Gu X, Cheng W, Tang X, Chen L, Ni B, Zhou R, Zhao Z, Wang Q, Zhou L 2020 Earth Planet. Phys. 4 238 Google Scholar
[25]	Zhou R, Gu X, Yang K, Li G, Ni B, Yi J, Chen L, Zhao F, Zhao Z, Wang Q, Zhou L 2020 Earth Planet. Phys. 4 120 Google Scholar
[26]	Vampola A L, Kuck G A 1978 J. Geophys. Res. 83 2543 Google Scholar
[27]	Koons H C, Edgar B C, Vampola A L 1981 J. Geophys. Res. 86 640 Google Scholar
[28]	Abel B, Thorne R M 1998 J. Geophys. Res. 103 2397 Google Scholar
[29]	Gamble R J, Rodger C J, Clilverd M A, Sauvaud J A, Thomson N R, Stewart S L, McCormick R J, Parrot M, Berthelier J J 2008 J. Geophys. Res. A 113 10211 Google Scholar
[30]	Graf K L, Inan U S, Piddyachiy D, Kulkarni P, Parrot M, Sauvaud J A 2009 J. Geophys. Res. A 114 07205 Google Scholar
[31]	Selesnick R S, Albert J M, Starks M J 2013 J. Geophys. Res. Space Phys. 118 628 Google Scholar
[32]	Agapitov O V, Artemyev A V, Mourenas D, Kasahara Y, Krasnoselskikh V 2014 J. Geophys. Res. Space Phys. 119 2876 Google Scholar
[33]	Claudepierre S G, Ma Q, Bortnik J, O'Brien T P, Fennell J F, Blake J B 2020 Geophys. Res. Lett. 47 e2019GL086056 Google Scholar
[34]	Imhof W L, Reagan J B, Voss H D, Gaines E E, Datlowe D W, Mobilia J, Helliwell R A, Inan U S, Katsufrakis J, Joiner R G 1983 Geophys. Res. Lett. 10 361 Google Scholar
[35]	Inan U S, Chang H C, Helliwell R A, Imhof W L, Reagan J B, Walt M 1985 J. Geophys. Res. 90 359 Google Scholar
[36]	王平, 王焕玉, 马宇蒨, 李新乔, 卢红, 孟祥承, 张吉龙, 王辉, 石峰, 徐岩冰, 于晓霞, 赵小芸, 吴峰 2011 60 039401 Google Scholar Wang P, Wang H Y, Ma Y Q, Li X Q, Lu H, Meng X C, Zhang J L, Wang H, Shi F, Xu Y B, Yu X X, Zhao X Y, Wu F 2011 Acta Phys. Sin. 60 039401 Google Scholar
[37]	Sauvaud J A, Maggiolo R, Jacquey C, Parrot M, Berthelier J J, Gamble R J, Rodger C J 2008 Geophys. Res. Lett. 35 L09101 Google Scholar
[38]	Clilverd M A, Rodger C J, Gamble R, Meredith N P, Parrot M, Berthelier J J, Thomson N R 2008 J. Geophys. Res. A 113 04211 Google Scholar
[39]	Kulkarni P, Inan U S, Bell T F, Bortnik J 2008 J. Geophys. Res. A 113 07214 Google Scholar
[40]	张振霞, 王辰宇, 李强, 吴书贵 2014 63 079401 Google Scholar Zhang Z X, Wang C Y, Li Q, Wu S G 2014 Acta Phys. Sin. 63 079401 Google Scholar
[41]	罗旭东, 牛胜利, 左应红 2015 64 069401 Google Scholar Luo X D, Niu S L, Zuo Y H 2015 Acta Phys. Sin. 64 069401 Google Scholar
[42]	Meredith N P, Horne R B, Clilverd M A, Ross J P J 2019 J. Geophys. Res. Space Phys. 124 5246 Google Scholar
[43]	Ozhogin P, Tu J, Song P, Reinisch B W 2012 J. Geophys. Res. A 117 06225 Google Scholar
[44]	Ni B, Thorne R M, Meredith N P, Shprits Y Y, Horne R B 2011 J. Geophys. Res. A 116 10207 Google Scholar
[45]	Ni B, Thorne R M, Shprits Y Y, Bortnik J 2008 Geophys. Res. Lett. 35 L11106 Google Scholar
[46]	Ma Q, Artemyev A V, Mourenas D, Li W, Thorne R M, Kletzing C A, Kurth W S, Hospodarsky G B, Reeves G D, Spence H E, Wygant J 2017 Geophys. Res. Lett. 44 12057
[47]	Xiao F, Su Z, Zheng H, Wang S 2009 J. Geophys. Res. A 114 03201 Google Scholar
[48]	Xiao F, Shen C, Wang Y, Zheng H, Wang S 2008 J. Geophys. Res. A 113 05203 Google Scholar

[1]	Liu Yang-Xi-Zi, Xiang Zheng, Zhou Chen, Ni Bin-Bin, Dong Jun-Hu, Hu Jing-Le, Wang Jian-Hang, Guo Hao-Zhi. Simulation study on “Wisp” electron spectra generated by NWC very low frequency transmitter signals. Acta Physica Sinica, 2024, 73(20): 209401. doi: 10.7498/aps.73.20240975
[2]	Wang Jing-Zhi, Ma Xin, Xiang Zheng, Gu Xu-Dong, Jiao Lu-Huai, Lei Liang-Jian, Ni Bin-Bin. Multi-dimensional modeling of radiation belt electron pitch-angle diffusion coefficients caused by plasmaspheric hiss. Acta Physica Sinica, 2022, 71(22): 229401. doi: 10.7498/aps.71.20220655
[3]	Yang Ju-Tao, Li Qing-Liang, Wang Jian-Guo, Hao Shu-Ji, Pan Wei-Yan. Theory of very low frequency/extra low frequency radiation by dual-beam beat wave heating ionosphere. Acta Physica Sinica, 2017, 66(1): 019401. doi: 10.7498/aps.66.019401
[4]	Luo Xu-Dong, Niu Sheng-Li, Zuo Ying-Hong. Diffusing loss effects of radiation belt energetic electrons caused by typical very low frequency electromagnetic wave. Acta Physica Sinica, 2015, 64(6): 069401. doi: 10.7498/aps.64.069401
[5]	Chang Shan-Shan, Ni Bin-Bin, Zhao Zheng-Yu, Wang Feng, Li Jin-Xing, Zhao Jing-Jing, Gu Xu-Dong, Zhou Chen. Test particle simulation of resonant interaction between energetic electrons in the magnetosphere and ELF/VLF waves generated by ionospheric modification. Acta Physica Sinica, 2014, 63(6): 069401. doi: 10.7498/aps.63.069401
[6]	Hao Shu-Ji, Li Qing-Liang, Yang Ju-Tao, Wu Zhen-Sen. Theory of ELF/VLF wave directional radiation by modulated heating of ionosphere. Acta Physica Sinica, 2013, 62(22): 229402. doi: 10.7498/aps.62.229402
[7]	Lü Yao-Ping, Gu Guo-Feng, Lu Hua-Chun, Dai Yu, Tang Guo-Ning. Refraction of reaction-diffusion plane wave for different diffusion coefficients. Acta Physica Sinica, 2009, 58(5): 2996-3000. doi: 10.7498/aps.58.2996
[8]	Gu Xu-Dong, Zhao Zheng-Yu, Ni Bin-Bin, Wang Xiang, Deng Feng. Quasi-linear diffusion of the radiation belt energetic electrons by ground-based HF heater-induced ELF/VLF emissions. Acta Physica Sinica, 2008, 57(10): 6673-6682. doi: 10.7498/aps.57.6673
[9]	Ni Bin-Bin, Zhao Zheng-Yu, Gu Xu-Dong, Wang Feng. Resonant diffusion of radiation belt energetic electrons by field-aligned propagation whistler-mode chorus waves. Acta Physica Sinica, 2008, 57(12): 7937-7949. doi: 10.7498/aps.57.7937
[10]	Liu Zhi-Ming, Cui Tian, Ma Yan-Ming, Liu Bing-Bing, Zou Guang-Tian. Interactions in Nb2H and its electronic structure. Acta Physica Sinica, 2007, 56(8): 4877-4883. doi: 10.7498/aps.56.4877
[11]	Yan Li-Fen, Wang Hong-Cheng, She Wei-Long. Influence of diffusion on the interaction between photovoltaic spatial solitons. Acta Physica Sinica, 2006, 55(10): 5257-5262. doi: 10.7498/aps.55.5257
[12]	Xu Miao-Hua, Liang Tian-Jiao, Zhang Jie. Bremsstrahlung diagnostics of hot electrons in laser-plasma interactions. Acta Physica Sinica, 2006, 55(5): 2357-2363. doi: 10.7498/aps.55.2357
[13]	Wei Qing, Wang Qi, Shi Jie-Long, Chen Yuan-Yuan. . Acta Physica Sinica, 2002, 51(1): 99-103. doi: 10.7498/aps.51.99
[14]	ZHAO DONG-HUAN. ANALYSIS OF EFFECTIVE TIME OF INTERACTION BETWEEN ELECTRON AND RADIATIVE WAVE IN THE FEL. Acta Physica Sinica, 1996, 45(4): 573-579. doi: 10.7498/aps.45.573
[15]	ZHAO DONG-HUAN. INTERACTIONS BETWEEN ELECTRONS WITH WAVES IN THE FEL AND ITS GAIN ANALYSIS. Acta Physica Sinica, 1994, 43(9): 1447-1454. doi: 10.7498/aps.43.1447
[16]	ZHANG XI-QING, ZHAO JIA-LONG, QIN WEI-PING, DOU KAI, HUANG SHI-HUA. MEASUREMENT OF THE AMBIPOLAR DIFFUSION COEFFICIENT USING TIME-DELAYED FOUR-WAVE MIXING WITH INCOHERENT LIGHT. Acta Physica Sinica, 1993, 42(3): 417-421. doi: 10.7498/aps.42.417
[17]	SUN XIN, CHEN HONG-YI, WU CHANG-QIN, FU RONG-TANG, FU ROU-LI. MATRIX ELEMENTS OF ELECTRON INTERACTION IN POLYMER. Acta Physica Sinica, 1991, 40(1): 102-108. doi: 10.7498/aps.40.102
[18]	He Xian-tu. NON-LINEAR EFFECT ON THE LARGE AMPLITUDE WAVES INTERACTION WITH PARTICLES OF LOW FREQUENCY OSCILLATION IN PLASMA. Acta Physica Sinica, 1982, 31(10): 1317-1336. doi: 10.7498/aps.31.1317
[19]	PAN WEI-YAN. INFLUENCE OF EARTH'S CURVATURE ON CALCULATION OF IONOSPHERE REFLECTION AT LF AND VLF BANDS. Acta Physica Sinica, 1981, 30(5): 661-670. doi: 10.7498/aps.30.661
[20]	. ВЗАИМОДЕЙСТВИЕ s-ЭЛЕКТРОНОВ СО СПИНОВЫМИ ВОЛНАМИ В ФЕРРОМАГНЕТИКЕ. Acta Physica Sinica, 1964, 20(3): 193-206. doi: 10.7498/aps.20.193

Catalog

Vol. 70, Issue 14 - 2021-07-20

Metrics

Abstract views: 4529
PDF Downloads: 97
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板