-
The high-speed flow passing through an open cavity will generate complex wave structures. The propagation and evolution of these waves can lead to the self-sustained oscillation of the cavity flow and cause strong noise. The cavity noise may contain multiple acoustic modes with discrete frequencies in the spectrum. A clear understanding of the evolution of the oscillation mode will provide a theoretical basis for the study of the noise control method. By analyzing the waves scattering process at both ends of the cavity at subsonic speed and supersonic speed and considering the three-dimensional spanwise flow, the three-dimensional wave model for subsonic cavity flow and supersonic cavity flow are established respectively. The model involves the nonlinear interaction between different waves in the cavity, which may produce other components different from the Rossiter mode. Based on the pressure signal data measured from the experiments on cavity flow for Mach numbers 0.9 and 1.5, the parameters in the model are linearly estimated. The pressure signals are analyzed by using FFT, bispectral analysis, and continuous wavelet transform. The results show that there are nonlinear interactions between the main oscillation modes, thus producing strong harmonics. The mode-switch phenomenon is observed in both the subsonic case and the supersonic case. The mode-switching exhibits low-frequency behavior and shows randomness as a whole.
-
Keywords:
- cavity flow /
- wave structures /
- mode behavior /
- aeroacoustics /
- time-frequency analysis
[1] Dix R, Bauer R 2000 AIAA Paper 2000
[2] Morton M 2007 AIAA Paper 2007
[3] Gloerfelt X, Bogey C, Bailly C 2007 Cavity Noise (Paris: Arts et Métiers ParisTech)
[4] Lawson S J, Barakos G N 2011 Prog. Aerosp. Sci 47 186
Google Scholar
[5] 郭启龙 2017 博士学位论文 (绵阳: 中国空气动力研究与发展中心研究生部)
Guo Q L 2017 Ph. D. Dissertation (Mianyang: China Aerodynamics Research and Development Center Graduate School) (in Chinese)
[6] Rossiter J E 1966 Aeron. Res. Counc. 3438
[7] Powell A 1961 J. Acoust. Soc. Am 33 395
Google Scholar
[8] Krishnamurty K 1956 Ph. D. Dissertation (Pasadena: California Institute of Technology)
[9] Heller H H, Holmes D G, Covert E E 1971 J. Sound Vib 18 545
Google Scholar
[10] Bilanin A J, Covert E E 1973 AIAA J 11 347
Google Scholar
[11] Block P J W 1976 NASA Tech. Note D
[12] Kerschen E, Tumin A 2003 AIAA Paper 2003
[13] Alvarez J, Kerschen E, Tumin A 2004 AIAA Paper 2004
[14] Ahuja K K, Mendoza J 1995 NASA C. R. 4653
[15] Mendoza J, Ahuja K K 1995 AIAA Paper 95
[16] Kegerise M A, Spina E F, Garg S, Cattafesta III L N 2004 Phys. Fluids 16 678
Google Scholar
[17] Brès G A, Colonius T 2008 J. Fluid Mech 599 309
Google Scholar
[18] Rowley C W, Colonius T, Basu A J 2002 J. Fluid Mech 455 315
Google Scholar
[19] Luo Y, Li H, Han S, Zhang S H 2021 Adv. Appl. Math. Mech 13 942
Google Scholar
[20] 韩帅斌, 罗勇, 李虎, 武从海, 张树海 2022 力学学报 54 359
Han S B, Luo Y, Li H, Wu C H, Zhang S H 2022 Chin. J. Theor. Appl. Mech. 54 359 (in Chinese)
[21] 韩帅斌, 罗勇, 张树海 2019航空工程进展 10 691
Han S B, Luo Y, Zhang S H 2019 Adv. Aero. Sci. Eng. 10 691 (in Chinese)
[22] Cattafesta III L N, Garg S, Kegerise M, Jones G S 1998 AIAA Paper 98
[23] Gloerfelt X, Bogey C, Bailly C 2003 Int. J. Aeroacoust 2 193
Google Scholar
[24] Thangamani V 2019 AIAA J 57 1
Google Scholar
[25] Luo Y, Wu C H, Yuan S Q, Tian H, Li H, Zhang S H 2021 32nd Congress of the International Council of the Aeronautical Sciences
[26] Kegerise M A 1999 Ph. D. Dissertation University
[27] Neary M D, Stephanoff K D 1987 Phys. Fluids 30 2936
Google Scholar
[28] 杨党国, 刘俊, 王显圣, 施傲, 周方奇, 郑晓东 2018 空气动力学学报 36 432
Yang D G, Liu J, Wang X S, Shi A, Zhou F Q, Zheng X D 2018 Acta Aerodyn. Sin. 36 432 (in Chinese)
[29] Nikias C L, Raghuveer M R 1987 Proc. IEEE 75 869
Google Scholar
[30] 胡广书 2013 现代信号处理 (第二版) (北京: 清华大学出版社)
Hu G S 2013 Modern Signal Processing (2nd Ed. ) (Beijing: Tsinghua University Press) (in Chinese)
-
图 1 亚声速空腔中波系结构示意图
Figure 1. Schematic diagram of wave structures of the subsonic cavity flow.
图 2 超声速空腔中波系结构示意图
Figure 2. Schematic diagram of wave structures of the supersonic cavity flow.
图 3 三维空腔实验模型示意图(单位: mm)
Figure 3. Schematic diagram of experimental cavity model (unit: mm).
图 4 M = 1.5, 空腔底部压力信号总声压级两次重复性实验结果对比
Figure 4. M = 1.5, comparison of two repeatable experiment results of OASPL of pressure signal at the bottom of cavity.
图 6 M = 1.5, 空腔前壁测点压力信号双谱分析相关系数 (a) 相关系数云图; (b) 局部放大
Figure 6. M = 1.5, bicoherence spectrum of the pressure perturbation signals at the front wall of the cavity: (a) Contours of the correlation coefficient; (b) locally zoomed region of panel (a).
图 7 两个马赫数的空腔前壁测点压力信号的连续小波变换结果 (a) M = 0.9 (注: 等值线范围(200, 3700)); (b) M = 1.5 (注: 等值线范围(300, 6000))
Figure 7. The CWT results of the pressure perturbation signals at the front wall of the cavity for two Mach numbers: (a) M = 0.9 (contour levels between 200 to 3700); (b) M = 1.5 (contour levels between 300 to 6000).
图 8 M = 0.9, 一阶、二阶模态小波变换系数随时间演化情况 (a) 一阶模态系数; (b) 二阶模态系数
Figure 8. M = 0.9, the amplitude of the CWT coefficients of the dominant modes extracted from the CWT result: (a) Coefficient of the first mode; (b) Coefficient of the second mode.
图 9 一阶、二阶模态小波变换系数的FFT频谱 (a) 一阶模态系数FFT; (b) 二阶模态系数FFT
Figure 9. The FFT results of the CWT coefficients of the dominant modes in Fig. 8: (a) FFT of the coefficient of the first mode; (b) FFT of the coefficient of the second mode.
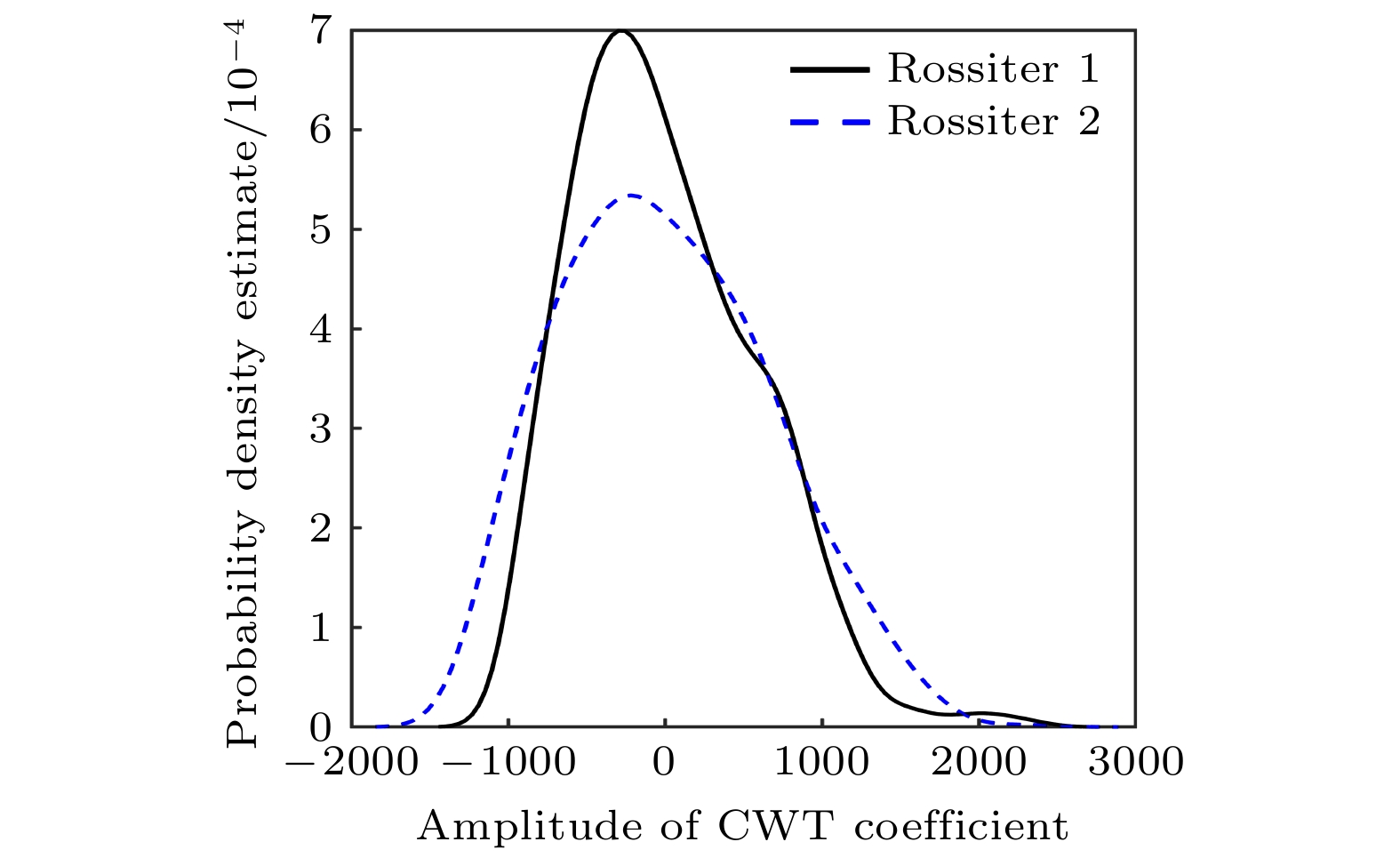
图 10 一阶、二阶模态小波变换系数的PDF
Figure 10. The probability density estimate of the CWT coefficients of the dominant modes in Fig. 8.
表 1 不同马赫数下的实验参数
Table 1. The experimental parameters for different cases
Case Mach number Pressure/
PaTemperature/K Reynold number(ReL) 1 0.9 67938.3 247.85 3.41 × 106 2 1.5 38080.2 198.62 4.28 × 106 
DownLoad: CSV
表 2 不同马赫数下的主导峰值频率
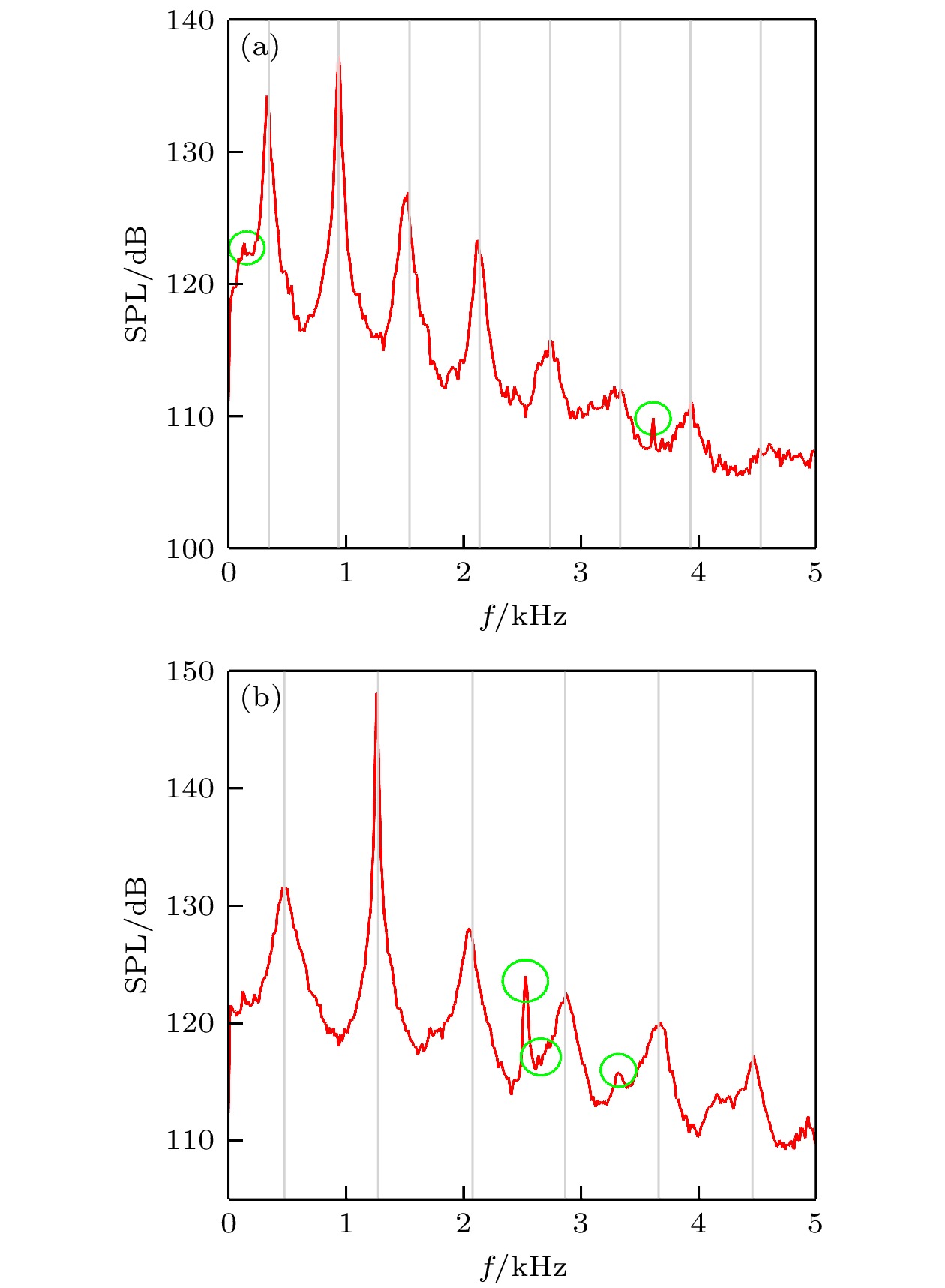
Table 2. The frequencies of the most energetic peaks for different cases.
Case f1 f2 f3 f4 f5 f6 f7 1 330 940 1500 2112 2735 3344 3925 2 480 1264 2042 2871 3673 4468 —
DownLoad: CSV
-
[1] Dix R, Bauer R 2000 AIAA Paper 2000
[2] Morton M 2007 AIAA Paper 2007
[3] Gloerfelt X, Bogey C, Bailly C 2007 Cavity Noise (Paris: Arts et Métiers ParisTech)
[4] Lawson S J, Barakos G N 2011 Prog. Aerosp. Sci 47 186
Google Scholar
[5] 郭启龙 2017 博士学位论文 (绵阳: 中国空气动力研究与发展中心研究生部)
Guo Q L 2017 Ph. D. Dissertation (Mianyang: China Aerodynamics Research and Development Center Graduate School) (in Chinese)
[6] Rossiter J E 1966 Aeron. Res. Counc. 3438
[7] Powell A 1961 J. Acoust. Soc. Am 33 395
Google Scholar
[8] Krishnamurty K 1956 Ph. D. Dissertation (Pasadena: California Institute of Technology)
[9] Heller H H, Holmes D G, Covert E E 1971 J. Sound Vib 18 545
Google Scholar
[10] Bilanin A J, Covert E E 1973 AIAA J 11 347
Google Scholar
[11] Block P J W 1976 NASA Tech. Note D
[12] Kerschen E, Tumin A 2003 AIAA Paper 2003
[13] Alvarez J, Kerschen E, Tumin A 2004 AIAA Paper 2004
[14] Ahuja K K, Mendoza J 1995 NASA C. R. 4653
[15] Mendoza J, Ahuja K K 1995 AIAA Paper 95
[16] Kegerise M A, Spina E F, Garg S, Cattafesta III L N 2004 Phys. Fluids 16 678
Google Scholar
[17] Brès G A, Colonius T 2008 J. Fluid Mech 599 309
Google Scholar
[18] Rowley C W, Colonius T, Basu A J 2002 J. Fluid Mech 455 315
Google Scholar
[19] Luo Y, Li H, Han S, Zhang S H 2021 Adv. Appl. Math. Mech 13 942
Google Scholar
[20] 韩帅斌, 罗勇, 李虎, 武从海, 张树海 2022 力学学报 54 359
Han S B, Luo Y, Li H, Wu C H, Zhang S H 2022 Chin. J. Theor. Appl. Mech. 54 359 (in Chinese)
[21] 韩帅斌, 罗勇, 张树海 2019航空工程进展 10 691
Han S B, Luo Y, Zhang S H 2019 Adv. Aero. Sci. Eng. 10 691 (in Chinese)
[22] Cattafesta III L N, Garg S, Kegerise M, Jones G S 1998 AIAA Paper 98
[23] Gloerfelt X, Bogey C, Bailly C 2003 Int. J. Aeroacoust 2 193
Google Scholar
[24] Thangamani V 2019 AIAA J 57 1
Google Scholar
[25] Luo Y, Wu C H, Yuan S Q, Tian H, Li H, Zhang S H 2021 32nd Congress of the International Council of the Aeronautical Sciences
[26] Kegerise M A 1999 Ph. D. Dissertation University
[27] Neary M D, Stephanoff K D 1987 Phys. Fluids 30 2936
Google Scholar
[28] 杨党国, 刘俊, 王显圣, 施傲, 周方奇, 郑晓东 2018 空气动力学学报 36 432
Yang D G, Liu J, Wang X S, Shi A, Zhou F Q, Zheng X D 2018 Acta Aerodyn. Sin. 36 432 (in Chinese)
[29] Nikias C L, Raghuveer M R 1987 Proc. IEEE 75 869
Google Scholar
[30] 胡广书 2013 现代信号处理 (第二版) (北京: 清华大学出版社)
Hu G S 2013 Modern Signal Processing (2nd Ed. ) (Beijing: Tsinghua University Press) (in Chinese)
DownLoad:
Catalog
Metrics
- Abstract views: 4391
- PDF Downloads: 53
- Cited By: 0
