-
By using the finite temperature field theory, the one-loop effective potential and the dynamics of the quantum chromodynamics deconfinement phase transition in the framework of Friedberg-Lee model are studied at finite temperature and density. Our results show that there is a first-order deconfinement phase transition for the full phase diagram, and the critical temperature is about 119.8 MeV for a zero chemical potential whereas the critical chemical is around 256.4 MeV when the temperature is fixed at T = 50 MeV. Moreover, in the thin-wall approximation, we investigate the dynamics of a strong first-order quark-hadron transition via homogeneous bubble nucleation in the Friedberg-Lee model. Under an appropriate boundary condition, the equation of motion for the
$ \sigma $ field is solved, then the evolutions of the bubble critical configuration with radius$ r $ at different temperatures and densities are calculated. The surface tension, the typical radius of the critical bubble and the shift in the coarse-grained free energy each as a function of temperature and chemical potential are obtained. In order to gain the reliability and advantages of the thin-wall approximation, our analytical results based on the thin-wall approximation are compared with those obtained by the exact numerical method accordingly. Finally, some consequences and possible applications of our results in the quark meson model and Polyakov quark meson model are also presented in the end of this paper.-
Keywords:
- quantum chromodynamics /
- Friedberg-Lee model /
- thin-wall approximation
[1] Fukushima K, Hatsuda T 2011 Rep. Prog. Phys. 74 014001
Google Scholar
[2] Gell-Mann M, Levy M 1960 Nuovo. Cimento. 16 705
Google Scholar
[3] Nambu Y, Jona-Lasinio G 1961 Phys. Rev. 122 345
Google Scholar
[4] Nambu Y, Jona-Lasinio G 1961 Phys. Rev. 124 246
Google Scholar
[5] Schaefer B J, Pawlowski J M, Wambach J 2007 Phys. Rev. D 76 074023
Google Scholar
[6] Costa P, Ruivo M C, Sousa C D, Hansen H 2010 Symmetry 2 1338
Google Scholar
[7] Coleman S 1977 Phys. Rev. D 15 2929
[8] Callan C G, Coleman J, Coleman S 1977 Phys. Rev. D 16 1762
Google Scholar
[9] Coleman S 1988 Aspects of Symmetry (Cambridge: Cambridge University Press)
[10] Linde A D 1981 Phys. Lett. B 100B 37
[11] Linde A D 1983 Nucl. Phys. B 216 421
Google Scholar
[12] Kohsuke Y, Tetsuo H, Yasuo M 2005 Quark-Gluon Plasma (Cambridge: Cambridge University Press)
[13] Friedberg R, Lee T D 1977 Phys. Rev. D 15 1694
Google Scholar
[14] Friedberg R, Lee T D 1977 Phys. Rev. D 16 1096
Google Scholar
[15] Friedberg R, Lee T D 1978 Phys. Rev. D 18 2623
Google Scholar
[16] Daniel C, Mark H, Weir D J 2018 Phys. Rev. D 97 123513
Google Scholar
[17] Cutting D, Escartin E G, Hindmarsh M, Weir D J 2021 Phys. Rev. D 103 023531
[18] Wang X, Huang F P, Zhang X 2020 JCAP 2005 045
[19] Bessa A, Fraga E S, Mintz B W 2008 Phys. Rev. D 79 034012
[20] Zhou S, Shu S, Mao H 2021 Chin. Phys. C 45 043104
Google Scholar
[21] Goldflam R, Wilets L 1982 Phys. Rev. D 25 1951
Google Scholar
[22] Reinhardt H, Dang B V, Schulz H 1985 Phys. Lett. B 159 161
Google Scholar
[23] Li M, Birse M C, Wilets L 1987 J. Phys. G 13 1
Google Scholar
[24] Gao S, Wang E, Jiarong L I 1992 Phys. Rev. D 46 3211
Google Scholar
[25] Mao H, Yao M, Zhao W Q 2008 Phys. Rev. C 77 065205
[26] Shu S, Li J R 2010 Phys. Rev. C 82 045203
[27] Birse M C 1992 Progr. Part. Nucl. Phys. 25 1
[28] Laine M, Vuorinen A 2016 Basics of Thermal Field Theory (New York: Springer International Publishing)
[29] Kapusta J I, Gale C 2006 Finite-Temperature Field Theory: Principles and Applications (Cambridge: Cambridge University Press)
[30] Coleman S 1988 Aspects of Symmetry (Cambridge: Cambridge University Press)
[31] Weinberg E J 2012 Classical Solutions in Quantum Field Theory: Solitons and Instantons in High Energy Physics (Cambridge: Cambridge Monographs on Mathematical Physics)
[32] Linde A D 1983 Nucl. Phys. B 216 421 Erratum: [1983 Nucl. Phys. B 223 544]
-
图 1 FL模型下的QCD相图结构
Figure 1. QCD phase diagram structure under FL model.
图 2 (a)
$ \mu = 0{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\text{MeV}} $ ,$ T = 0, 70, 100, 105, 109{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\text{MeV}} $ 时气泡临界位形; (b)$ T = 50{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\text{MeV}} $ ,$\mu = 0, 150, 200, 230, 240{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\text{MeV}}$ 时气泡临界位形Figure 2. (a) Bubble critical configuration at
$ \mu = 0{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\text{MeV}} $ ,$ T = 0, 70, 100, 105, 109{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\text{MeV}} $ ; (b) bubble critical configuration at$ T = 50{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\text{MeV}} $ ,$ \mu = 0, 150, 200, 230, 240{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\text{MeV}} $ .
图 3
$ T = {T_{\text{c}}} $ 时表面张力随化学势$ \mu $ 的变化关系Figure 3. Surface tension as a function of chemical potential
$ \mu $ when$ T = {T_{\text{c}}} $ .
图 4 (a)
$ \mu = 0{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\text{MeV}} $ 时表面张力与温度$ T $ 的关系; (b) T =$ 50{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\text{MeV}}$ 时表面张力与化学势$ \mu $ 的关系Figure 4. (a) Surface tension as a function of temperature
$ T $ when$ \mu = 0{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\text{MeV}} $ ; (b) surface tension as a function of chemical potential$ \mu $ when$ T = 50{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\text{MeV}} $ .
图 5 (a)
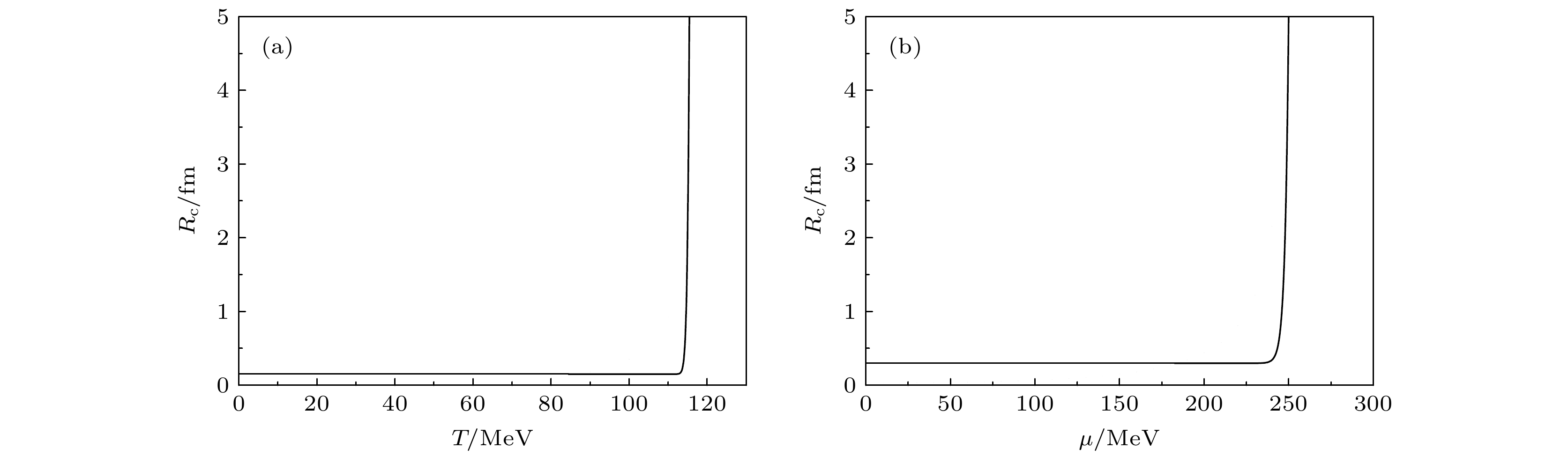
$ \mu = 0{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\text{MeV}} $ 时临界半径与温度$ T $ 的关系; (b)$ T = 50{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\text{MeV}} $ 时临界半径与化学势$ \mu $ 的关系Figure 5. (a) Typical radius of the critical bubble as a function of temperature
$ T $ when$ \mu = 0{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\text{MeV}} $ ; (b) typical radius of the critical bubble as a function of chemical potential$ \mu $ when$ T = 50{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\text{MeV}} $ .
图 6 (a)
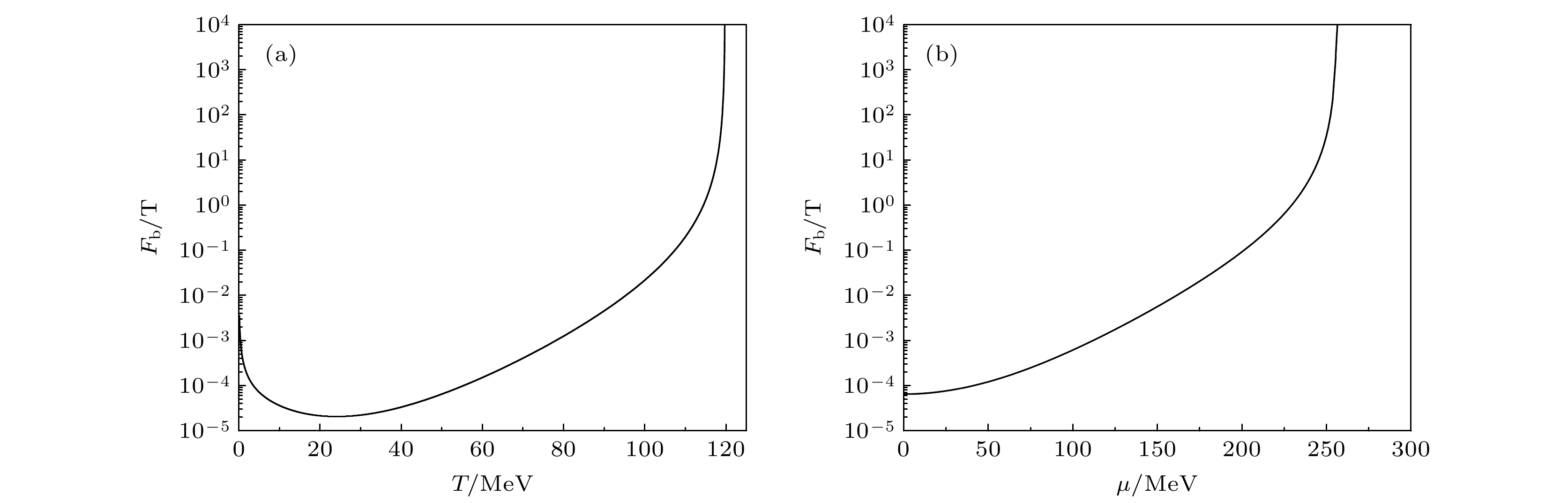
$ \mu = 0{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\text{MeV}} $ 时$ {F_{\text{b}}}/T $ 与温度$ T $ 的关系; (b)$ T = 50{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\text{MeV}} $ 时$ {F_{\text{b}}}/T $ 与化学势$ \mu $ 的关系Figure 6. (a)
$ {F_{\text{b}}}/T $ as a function of temperature$ T $ when$ \mu = 0{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\text{MeV}} $ ; (b)$ {F_{\text{b}}}/T $ as a function of chemical potential$ \mu $ when$ T = 50{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\text{MeV}} $ . -
[1] Fukushima K, Hatsuda T 2011 Rep. Prog. Phys. 74 014001
Google Scholar
[2] Gell-Mann M, Levy M 1960 Nuovo. Cimento. 16 705
Google Scholar
[3] Nambu Y, Jona-Lasinio G 1961 Phys. Rev. 122 345
Google Scholar
[4] Nambu Y, Jona-Lasinio G 1961 Phys. Rev. 124 246
Google Scholar
[5] Schaefer B J, Pawlowski J M, Wambach J 2007 Phys. Rev. D 76 074023
Google Scholar
[6] Costa P, Ruivo M C, Sousa C D, Hansen H 2010 Symmetry 2 1338
Google Scholar
[7] Coleman S 1977 Phys. Rev. D 15 2929
[8] Callan C G, Coleman J, Coleman S 1977 Phys. Rev. D 16 1762
Google Scholar
[9] Coleman S 1988 Aspects of Symmetry (Cambridge: Cambridge University Press)
[10] Linde A D 1981 Phys. Lett. B 100B 37
[11] Linde A D 1983 Nucl. Phys. B 216 421
Google Scholar
[12] Kohsuke Y, Tetsuo H, Yasuo M 2005 Quark-Gluon Plasma (Cambridge: Cambridge University Press)
[13] Friedberg R, Lee T D 1977 Phys. Rev. D 15 1694
Google Scholar
[14] Friedberg R, Lee T D 1977 Phys. Rev. D 16 1096
Google Scholar
[15] Friedberg R, Lee T D 1978 Phys. Rev. D 18 2623
Google Scholar
[16] Daniel C, Mark H, Weir D J 2018 Phys. Rev. D 97 123513
Google Scholar
[17] Cutting D, Escartin E G, Hindmarsh M, Weir D J 2021 Phys. Rev. D 103 023531
[18] Wang X, Huang F P, Zhang X 2020 JCAP 2005 045
[19] Bessa A, Fraga E S, Mintz B W 2008 Phys. Rev. D 79 034012
[20] Zhou S, Shu S, Mao H 2021 Chin. Phys. C 45 043104
Google Scholar
[21] Goldflam R, Wilets L 1982 Phys. Rev. D 25 1951
Google Scholar
[22] Reinhardt H, Dang B V, Schulz H 1985 Phys. Lett. B 159 161
Google Scholar
[23] Li M, Birse M C, Wilets L 1987 J. Phys. G 13 1
Google Scholar
[24] Gao S, Wang E, Jiarong L I 1992 Phys. Rev. D 46 3211
Google Scholar
[25] Mao H, Yao M, Zhao W Q 2008 Phys. Rev. C 77 065205
[26] Shu S, Li J R 2010 Phys. Rev. C 82 045203
[27] Birse M C 1992 Progr. Part. Nucl. Phys. 25 1
[28] Laine M, Vuorinen A 2016 Basics of Thermal Field Theory (New York: Springer International Publishing)
[29] Kapusta J I, Gale C 2006 Finite-Temperature Field Theory: Principles and Applications (Cambridge: Cambridge University Press)
[30] Coleman S 1988 Aspects of Symmetry (Cambridge: Cambridge University Press)
[31] Weinberg E J 2012 Classical Solutions in Quantum Field Theory: Solitons and Instantons in High Energy Physics (Cambridge: Cambridge Monographs on Mathematical Physics)
[32] Linde A D 1983 Nucl. Phys. B 216 421 Erratum: [1983 Nucl. Phys. B 223 544]
DownLoad:
Catalog
Metrics
- Abstract views: 3586
- PDF Downloads: 60
- Cited By: 0
