-
The dynamical properties of quantum spin systems are a hot topic of research in statistical and condensed matter physics. In this paper, the dynamics of one-dimensional quantum Ising model with both transverse and longitudinal magnetic field (LMF) is investigated by the recursion method. The time-dependent spin autocorrelation function $C\left( t \right) = \overline {\left\langle {\sigma _j^x\left( t \right)\sigma _j^x\left( 0 \right)} \right\rangle } $ and corresponding spectral density$\varPhi \left( \omega \right)$ are calculated. The Hamiltonian of the model system can be written as$H = - \dfrac{1}{2}J\displaystyle\sum\limits_i^N {\sigma _i^x\sigma _{i + 1}^x - \dfrac{1}{2}\displaystyle\sum\limits_i^N {B_i^x\sigma _i^x} } - \dfrac{1}{2}\displaystyle\sum\limits_i^N {B_i^z\sigma _i^z}$ .This work focuses mainly on the effects of LMF ( $ B_i^x $ ) on spin dynamics of the Ising system, and both uniform LMF and random LMF are considered respectively. Without loss of generality, the transverse magnetic field$ B_i^z = 1 $ is set in the numerical calculation, which fixes the energy scale.The results show that the uniform LMF can induce crossovers between different dynamical behaviors (e.g. independent spins precessing, collective-mode behavior or central-peak behavior) and drive multiple vibrational modes (multiple-peaked behavior) when spin interaction ( $ J $ ) is weak. However, the effect of uniform LMF is not obvious when spin interaction is strong. For the case of random LMF, the effects of bimodal-type and Gaussian-type random LMF are investigated, respectively. The dynamical results under the two types of random LMFs are quite different and highly dependent on many factors, such as the mean values ($ {B_1} $ ,$ {B_2} $ and$ {B_x} $ ) or the standard deviation ($ \sigma $ ) of random distributions. The nonsymmetric bimodal-type random LMF ($ {B_1} \ne {B_2} $ ) may induce new vibrational modes easily. The dynamical behaviors under the Gaussian-type random LMF are more abundant than under the bimodal-type random LMF. When$ \sigma $ is small, the system undergoes two crossovers: from a collective-mode behavior to a double-peaked behavior, and then to a central-peak behavior as the mean value$ {B_x} $ increases. However, when$ \sigma $ is large, the system presents only a central-peak behavior.For both cases of uniform LMF and random LMF, it is found that the central-peak behavior of the system is maintained when the proportion of LMF is large. This conclusion can be generalized that the emergence of noncommutative terms (noncommutative with the transverse-field term $\displaystyle\sum\nolimits_i^N {B_i^z\sigma _i^z}$ ) in Hamiltonian will enhance the central peak behavior. Therefore, noncommutative terms, such as next-nearest-neighbor spin interactions, Dzyaloshinskii-Moryia interactions, impurities, four-spin interactions, etc., can be added to the system Hamiltonian to modulate the dynamical properties. This provides a new direction for the future study of spin dynamics.-
Keywords:
- Ising model /
- longitudinal magnetic field /
- spin autocorrelation function /
- spectral density
[1] Plascak J A, Pires A S T, Sá Barreto F C 1982 Solid State Commun. 44 787
Google Scholar
[2] Plascak J A, Sá Barreto F C, Pires A S T, Goncalves L L 1983 J. Phys. C: Solid State Phys. 16 49
Google Scholar
[3] Watarai S, Matsubara T 1984 J Phys. Soc. Jpn. 53 3648
Google Scholar
[4] Levitsky R R, Zachek I R, Mits E V, Grigas J, Paprotny W 1986 Ferroelectrics 67 109
Google Scholar
[5] Wu W, Ellman B, Rosenbaum T F, Aeppli G, Reich D H 1991 Phys. Rev. Lett. 67 2076
[6] Chernodub M N, Lundgren M, Niemi A J 2011 Phys. Rev. E 83 011126
Google Scholar
[7] Storm C, Nelson P C 2003 Phys. Rev. E 67 051906
[8] Faure Q, Takayoshi S, Petit S, Simonet V, Raymond S, Regnault L P, Boehm M, White J S, Månsson M, Rüegg C, Lejay P, Canals B, Lorenz T, Furuya S C, Giamarchi T, Grenier B 2018 Nature Phys. 14 716
Google Scholar
[9] Jia X, Chakravarty S 2006 Phys. Rev. B 74 172414
Google Scholar
[10] Rønnow H M, Parthasarathy R, Jensen J, Aeppli G, Rosenbaum T F, McMorrow D F 2005 Science 308 389
[11] Fogedby H C 1978 J. Phys. C: Solid State Phys. 11 2801
Google Scholar
[12] Sen S, Mahanti S D, Cai Z X 1991 Phys. Rev. B 43 10990
Google Scholar
[13] Sen P 1997 Phys. Rev. B 55 11367
Google Scholar
[14] Osenda O, Huang Z, Kais S 2003 Phys. Rev. A 67 062321
Google Scholar
[15] Florencio J, Sá Barreto F C 1999 Phys. Rev. B 60 9555
Google Scholar
[16] Chen S X, Shen Y Y, Kong X M 2010 Phys. Rev. B 82 174404
[17] Da Conceição C M S, Maia R N P 2017 Phys. Rev. E 96 032121
[18] von Ohr S, Manssen M, Hartmann A K 2017 Phys. Rev. E 96 013315
Google Scholar
[19] Hadjiagapiou I A 2011 Physica A 390 2229
Google Scholar
[20] Liu Z Q, Kong X M, Chen X S 2006 Phys. Rev. B 73 224412
Google Scholar
[21] Theodorakis P E, Georgiou I, Fytas N G 2013 Phys. Rev. E 87 032119
[22] Crokidakis N, Nobre F D 2008 J. Phys.: Condens. Matter 20 145211
[23] Liu Z Q, Jiang S R, Kong X M 2014 Chin. Phys. B 23 087505
Google Scholar
[24] Kenzelmann M, Coldea R, Tennant D A, Visser D, Hofmann M, Smeibidl P, Tylczynski Z 2002 Phys. Rev. B 65 144432
Google Scholar
[25] Simon J, Bakr W S, Ma R, Tai M E, Preiss P M, Greiner M 2011 Nature 472 307
Google Scholar
[26] Senthil T 1998 Phys. Rev. B 57 8375
Google Scholar
[27] Dmitriev D V, Krivnov V Y 2004 Phys. Rev. B 70 144414
Google Scholar
[28] Neto M A, De Sousa J R 2013 Physica A 392 1
Google Scholar
[29] Corrêa Silva E V, Skea J E F, Rojas O, De Souza S M, Thomaz M T 2008 Physica A 387 5117
Google Scholar
[30] Do Nascimento D A, Neto M A, De Sousa J R, Pacobahyba J T 2012 J. Magn. Magn. Mater. 324 2429
[31] Do Nascimento D A, Pacobahyba J T, Neto M A, Salmon O D R, Plascak J A 2017 Physica A 474 224
[32] Zhao Z Y, Liu X G, He Z Z, Wang X M, Fan C, Ke W P, Li Q J, Chen L M, Zhao X, Sun X F 2012 Phys. Rev. B 85 134412
Google Scholar
[33] Kopeć T K, Usadel K D, Büttner G 1989 Phys. Rev. B 39 12418
[34] Ovchinnikov A A, Dmitriev D V, Krivnov V Y, Cheranovskii V O 2003 Phys. Rev. B 68 214406
Google Scholar
[35] Liu Z Q, Jiang S R, Kong X M, Xu Y L 2017 Physica A 473 536
[36] Viswanath V S, Müller G 1994 The Recursion Method—Application to Many-body Dynamics (Berlin: Springe-Verlag)
[37] Mezei F, Murani A P 1979 J. Magn. Magn. Mater. 14 211
Google Scholar
[38] Lee M H 1982 Phys. Rev. Lett. 49 1072
Google Scholar
[39] Lee M H 1982 Phys. Rev. B 26 2547
Google Scholar
[40] Lee M H 2000 Phys. Rev. E 62 1769
Google Scholar
[41] Florencio J, De Alcantara Bonfim O F 2020 Front. Phys. 8 557277
Google Scholar
[42] Sur A, Jasnow D, Lowe I J 1975 Phys. Rev. B 12 3845
Google Scholar
[43] Yuan X J, Kong X M, Xu Z B, Liu Z Q 2010 Physica A 389 242
Google Scholar
[44] 袁晓娟, 赵邦宇, 陈淑霞, 孔祥木 2010 59 1499
Google Scholar
Yuan X J, Zhao B Y, Chen S X, Kong X M 2010 Acta Phys. Sin. 59 1499
Google Scholar
[45] Nunes M E S, De Mello Silva É, Martins P H L, Plascak J A, Florencio J 2018 Phys. Rev. E 98 042124
[46] Li Y F, Kong X M 2013 Chin. Phys. B 22 037502
Google Scholar
[47] 李银芳, 申银阳, 孔祥木 2012 61 107501
Google Scholar
Li Y F, She Y Y, Kong X M 2012 Acta Phys. Sin. 61 107501
Google Scholar
[48] Huang X, Yang Z 2015 Solid State Commun. 204 28
Google Scholar
[49] De Souza W L, De Mello Silva É, Martins P H L 2020 Phys. Rev. E 101 042104
-
图 1 横场取值
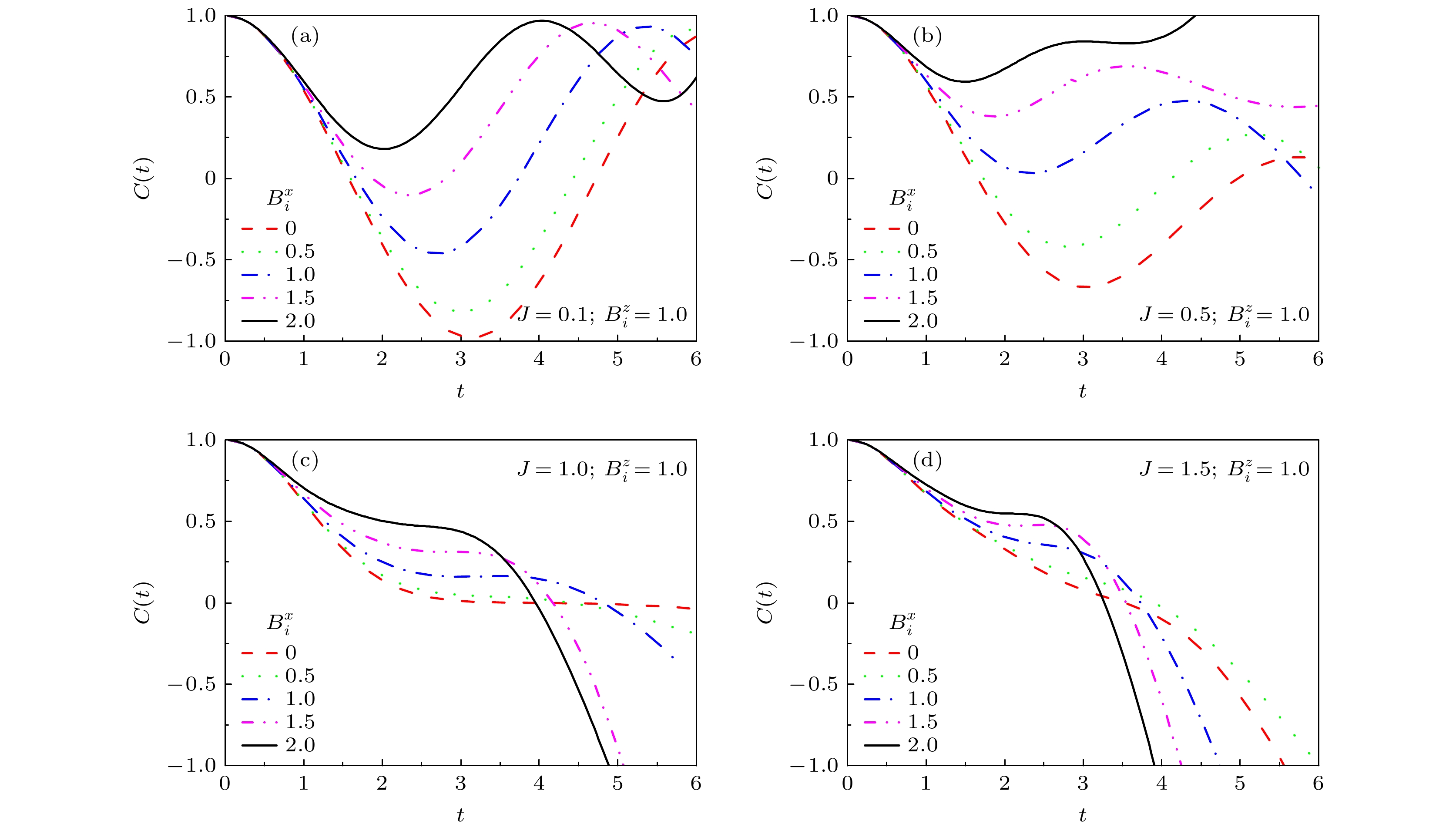
$B_i^z = 1$ , 纵场取值$ B_i^x = 0 $ , 0.5, 1.0, 1.5和2.0, (a)−(d)分别对应自旋耦合相互作用参数J = 0.1, 0.5, 1.0和1.5时的自旋关联函数Figure 1. Take the transverse magnetic field
$B_i^z = 1$ and the longitudinal magnetic field$ B_i^x = 0 $ , 0.5, 1.0, 1.5 and 2.0, respectively. Spin autocorrelation functions$C\left( t \right)$ for different values of spin interactions (e.g., J = 0.1, 0.5, 1.0 and 1.5) are given in (a)−(d), respectively.
图 2 横场取值
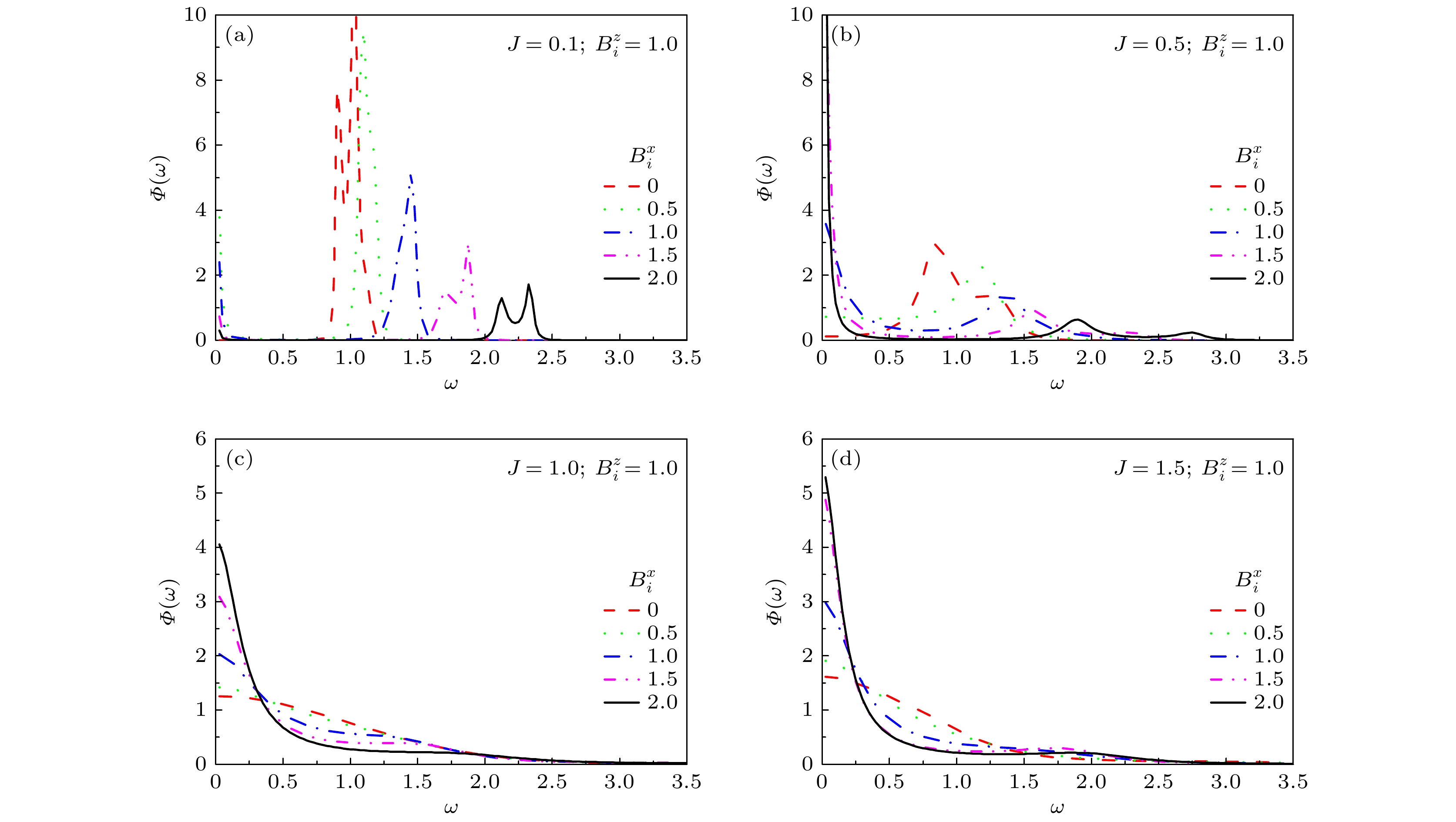
$B_i^z = 1$ , 纵场取值$ B_i^x = 0 $ , 0.5, 1.0, 1.5和2.0, (a)−(d)分别对应自旋耦合相互作用参数J = 0.1, 0.5, 1.0和1.5时的谱密度.Figure 2. Take the transverse magnetic field
$B_i^z = 1$ and the longitudinal magnetic field$ B_i^x = 0 $ , 0.5, 1.0, 1.5 and 2.0, respectively. The corresponding spectral density$\varPhi \left( \omega \right)$ for different values of spin interactions (e.g., J = 0.1, 0.5, 1.0 and 1.5) are given in (a)−(d), respectively.
图 3 随机纵场满足双模分布时的自旋关联函数和谱密度 (a), (b)对应
$ {B_1} = 1.3 $ 和$ {B_2} = 0.7 $ 时的结果; (c), (d)为$ {B_1} = 1.8 $ 和$ {B_2} = 0.2 $ 时的结果Figure 3. Spin autocorrelation functions and the corresponding spectral densities for bimodal-type random longitudinal magnetic field. The results for
$ {B_1} = 1.3 $ and$ {B_2} = 0.7 $ are given in (a) and (b), and the results for$ {B_1} = 1.8 $ and$ {B_2} = 0.2 $ are given in (c) and (d), respectively.
图 4 随机纵场满足高斯分布时的谱密度 (a)−(d)分别对应
$ \sigma = 0.3, {\text{ }}0.8, {\text{ }}1.0, {\text{ }}1.8 $ 时的结果.Figure 4. Spectral densities for Gaussian-type random longitudinal magnetic field. The results for
$ \sigma = 0.3, {\text{ }}0.8, {\text{ }}1.0 $ and 1.8 are given in (a)−(d), respectively. -
[1] Plascak J A, Pires A S T, Sá Barreto F C 1982 Solid State Commun. 44 787
Google Scholar
[2] Plascak J A, Sá Barreto F C, Pires A S T, Goncalves L L 1983 J. Phys. C: Solid State Phys. 16 49
Google Scholar
[3] Watarai S, Matsubara T 1984 J Phys. Soc. Jpn. 53 3648
Google Scholar
[4] Levitsky R R, Zachek I R, Mits E V, Grigas J, Paprotny W 1986 Ferroelectrics 67 109
Google Scholar
[5] Wu W, Ellman B, Rosenbaum T F, Aeppli G, Reich D H 1991 Phys. Rev. Lett. 67 2076
[6] Chernodub M N, Lundgren M, Niemi A J 2011 Phys. Rev. E 83 011126
Google Scholar
[7] Storm C, Nelson P C 2003 Phys. Rev. E 67 051906
[8] Faure Q, Takayoshi S, Petit S, Simonet V, Raymond S, Regnault L P, Boehm M, White J S, Månsson M, Rüegg C, Lejay P, Canals B, Lorenz T, Furuya S C, Giamarchi T, Grenier B 2018 Nature Phys. 14 716
Google Scholar
[9] Jia X, Chakravarty S 2006 Phys. Rev. B 74 172414
Google Scholar
[10] Rønnow H M, Parthasarathy R, Jensen J, Aeppli G, Rosenbaum T F, McMorrow D F 2005 Science 308 389
[11] Fogedby H C 1978 J. Phys. C: Solid State Phys. 11 2801
Google Scholar
[12] Sen S, Mahanti S D, Cai Z X 1991 Phys. Rev. B 43 10990
Google Scholar
[13] Sen P 1997 Phys. Rev. B 55 11367
Google Scholar
[14] Osenda O, Huang Z, Kais S 2003 Phys. Rev. A 67 062321
Google Scholar
[15] Florencio J, Sá Barreto F C 1999 Phys. Rev. B 60 9555
Google Scholar
[16] Chen S X, Shen Y Y, Kong X M 2010 Phys. Rev. B 82 174404
[17] Da Conceição C M S, Maia R N P 2017 Phys. Rev. E 96 032121
[18] von Ohr S, Manssen M, Hartmann A K 2017 Phys. Rev. E 96 013315
Google Scholar
[19] Hadjiagapiou I A 2011 Physica A 390 2229
Google Scholar
[20] Liu Z Q, Kong X M, Chen X S 2006 Phys. Rev. B 73 224412
Google Scholar
[21] Theodorakis P E, Georgiou I, Fytas N G 2013 Phys. Rev. E 87 032119
[22] Crokidakis N, Nobre F D 2008 J. Phys.: Condens. Matter 20 145211
[23] Liu Z Q, Jiang S R, Kong X M 2014 Chin. Phys. B 23 087505
Google Scholar
[24] Kenzelmann M, Coldea R, Tennant D A, Visser D, Hofmann M, Smeibidl P, Tylczynski Z 2002 Phys. Rev. B 65 144432
Google Scholar
[25] Simon J, Bakr W S, Ma R, Tai M E, Preiss P M, Greiner M 2011 Nature 472 307
Google Scholar
[26] Senthil T 1998 Phys. Rev. B 57 8375
Google Scholar
[27] Dmitriev D V, Krivnov V Y 2004 Phys. Rev. B 70 144414
Google Scholar
[28] Neto M A, De Sousa J R 2013 Physica A 392 1
Google Scholar
[29] Corrêa Silva E V, Skea J E F, Rojas O, De Souza S M, Thomaz M T 2008 Physica A 387 5117
Google Scholar
[30] Do Nascimento D A, Neto M A, De Sousa J R, Pacobahyba J T 2012 J. Magn. Magn. Mater. 324 2429
[31] Do Nascimento D A, Pacobahyba J T, Neto M A, Salmon O D R, Plascak J A 2017 Physica A 474 224
[32] Zhao Z Y, Liu X G, He Z Z, Wang X M, Fan C, Ke W P, Li Q J, Chen L M, Zhao X, Sun X F 2012 Phys. Rev. B 85 134412
Google Scholar
[33] Kopeć T K, Usadel K D, Büttner G 1989 Phys. Rev. B 39 12418
[34] Ovchinnikov A A, Dmitriev D V, Krivnov V Y, Cheranovskii V O 2003 Phys. Rev. B 68 214406
Google Scholar
[35] Liu Z Q, Jiang S R, Kong X M, Xu Y L 2017 Physica A 473 536
[36] Viswanath V S, Müller G 1994 The Recursion Method—Application to Many-body Dynamics (Berlin: Springe-Verlag)
[37] Mezei F, Murani A P 1979 J. Magn. Magn. Mater. 14 211
Google Scholar
[38] Lee M H 1982 Phys. Rev. Lett. 49 1072
Google Scholar
[39] Lee M H 1982 Phys. Rev. B 26 2547
Google Scholar
[40] Lee M H 2000 Phys. Rev. E 62 1769
Google Scholar
[41] Florencio J, De Alcantara Bonfim O F 2020 Front. Phys. 8 557277
Google Scholar
[42] Sur A, Jasnow D, Lowe I J 1975 Phys. Rev. B 12 3845
Google Scholar
[43] Yuan X J, Kong X M, Xu Z B, Liu Z Q 2010 Physica A 389 242
Google Scholar
[44] 袁晓娟, 赵邦宇, 陈淑霞, 孔祥木 2010 59 1499
Google Scholar
Yuan X J, Zhao B Y, Chen S X, Kong X M 2010 Acta Phys. Sin. 59 1499
Google Scholar
[45] Nunes M E S, De Mello Silva É, Martins P H L, Plascak J A, Florencio J 2018 Phys. Rev. E 98 042124
[46] Li Y F, Kong X M 2013 Chin. Phys. B 22 037502
Google Scholar
[47] 李银芳, 申银阳, 孔祥木 2012 61 107501
Google Scholar
Li Y F, She Y Y, Kong X M 2012 Acta Phys. Sin. 61 107501
Google Scholar
[48] Huang X, Yang Z 2015 Solid State Commun. 204 28
Google Scholar
[49] De Souza W L, De Mello Silva É, Martins P H L 2020 Phys. Rev. E 101 042104
DownLoad:
Catalog
Metrics
- Abstract views: 4235
- PDF Downloads: 74
- Cited By: 0
