-
It is of fundamental importance to know the dynamics of quantum spin systems immersed in external magnetic fields. In this work, the dynamical properties of one-dimensional quantum Ising model with trimodal random transverse and longitudinal magnetic fields are investigated by the recursion method. The spin correlation function $C\left( t \right) = \overline {\left\langle {\sigma _j^x\left( t \right)\sigma _j^x\left( 0 \right)} \right\rangle } $ and the corresponding spectral density$\varPhi \left( \omega \right) = \displaystyle\int_{ - \infty }^{ + \infty } {{\rm{d}}t{{\rm{e}}^{{\rm{i}}\omega t}}C\left( t \right)}$ are calculated. The model Hamiltonian can be written as$ H = - \dfrac{1}{2}J\displaystyle\sum\limits_i^N {\sigma _i^x\sigma _{i + 1}^x} - \dfrac{1}{2}\displaystyle\sum\limits_i^N {{B_{iz}}\sigma _i^z} - \dfrac{1}{2}\sum\limits_i^N {{B_{ix}}\sigma _i^x} $ ,where $\sigma _i^\alpha \left( {\alpha = x,y,z} \right)$ are Pauli matrices at site$ i $ ,$J$ is the nearest-neighbor exchange coupling.$ {B_{iz}} $ and$ {B_{ix}} $ denote the transverse and longitudinal magnetic field, respectively. They satisfy the following trimodal distribution,$ \rho \left( {{B_{iz}}} \right) = p\delta ({B_{iz}} - {B_p}) + q\delta ({B_{iz}} - {B_q}) + r\delta ({B_{iz}}) $ ,$ \rho \left( {{B_{ix}}} \right) = p\delta ({B_{ix}} - {B_p}) + q\delta ({B_{ix}} - {B_q}) + r\delta ({B_{ix}}). $ The value intervals of the coefficients $p$ ,$q$ and$r$ are all [0,1], and the coefficients satisfy the constraint condition$ p + q + r = 1 $ .For the case of trimodal random $ {B_{iz}} $ (consider$ {B_{ix}} \equiv 0 $ for simplicity), the exchange couplings are assumed to be$J \equiv 1$ to fix the energy scale, and the reference values are set as follows:$ {B_p} = 0.5 < J $ and$ {B_q} = 1.5 > J $ . The coefficient$r$ can be considered as the proportion of non-magnetic impurities. When$r = 0$ , the trimodal distribution reduces into the bimodal distribution. The dynamics of the system exhibits a crossover from the central-peak behavior to the collective-mode behavior as$q$ increases, which is consistent with the value reported previously. As$r$ increases, the crossover between different dynamical behaviors changes obviously (e.g. the crossover from central-peak to double-peak when$r = 0.2$ ), and the presence of non-magnetic impurities favors low-frequency response. Owing to the competition between the non-magnetic impurities and transverse magnetic field, the system tends to exhibit multi-peak behavior in most cases, e.g.$r = 0.4$ , 0.6 or 0.8. However, the multi-peak behavior disappears when$r \to 1$ . That is because the system's response to the transverse field is limited when the proportion of non-magnetic impurities is large enough. Interestingly, when the parameters satisfy$ q{B_q} = p{B_p} $ , the central-peak behavior can be maintained. What makes sense is that the conclusion is universal.For the case of trimodal random $ {B_{ix}} $ , the coefficient$r$ no longer represents the proportion of non-magnetic impurities when$ {B_{ix}} $ and$ {B_{iz}} $ ($ {B_{iz}} \equiv 1 $ ) coexist here. In the case of weak exchange coupling, the effect of longitudinal magnetic field on spin dynamics is obvious, so$J \equiv 0.5$ is set here. The reference values are set below:$ {B_p} = 0.5 \lt {B_{iz}} $ and$ {B_q} = 1.5 \gt {B_{iz}} $ . When$r$ is small ($r = 0$ , 0.2 or 0.4), the system undergoes a crossover from the collective-mode behavior to the double-peak behavior as$q$ increases. However, the low-frequency responses gradually disappear, while the high-frequency responses are maintained as$r$ increases. Take the case of$ r = 0.8 $ for example, the system only presents a collective-mode behavior. The results indicate that increasing$r$ is no longer conducive to the low-frequency response, which is contrary to the case of trimodal random$ {B_{iz}} $ . The$r$ branch only regulates the intensity of the trimodal random$ {B_{ix}} $ . Our results indicate that using trimodal random magnetic field to manipulate the spin dynamics of the Ising system may be a new try.-
Keywords:
- Ising model /
- trimodal distribution /
- spin correlation function /
- spectral density
[1] Kenzelmann M, Coldea R, Tennant D A, Visser D, Hofmann M, Smeibidl P, Tylczynski Z 2002 Phys. Rev. B 65 144432
Google Scholar
[2] Zhao Z Y, Liu X G, He Z Z, Wang X M, Fan C, Ke W P, Li Q J, Chen L M, Zhao X, Sun X F 2012 Phys. Rev. B 85 134412
Google Scholar
[3] Cui Y, Zou H, Xi N, He Z, Yang Y X, Shu L, Zhang G H, Hu Z, Chen T, Yu R, Wu J and Yu W 2019 Phys. Rev. Lett. 123 067203
Google Scholar
[4] Simon J, Bakr W S, Ma R, Tai M E, Preiss P M, Greiner M 2011 Nature 472 307
Google Scholar
[5] Dmitriev D V, Krivnov V Y 2004 Phys. Rev. B 70 144414
Google Scholar
[6] Neto M A, De Sousa J R 2013 Physica A 392 1
Google Scholar
[7] Corrêa Silva E V, Skea J E F, Rojas O, De Souza S M, Thomaz M T 2008 Physica A 387 5117
Google Scholar
[8] Do Nascimento D A, Neto M A, De Sousa J R, Pacobahyba J T 2012 J. Magn. Magn. Mater. 324 2429
Google Scholar
[9] Do Nascimento D A, Pacobahyba J T, Neto M A, Salmon O D R, Plascak J A 2017 Physica A 474 224
Google Scholar
[10] Senthil T 1998 Phys. Rev. B 57 8375
Google Scholar
[11] Liu Z Q, Jiang S R, Kong X M, Xu Y L 2017 Physica A 473 536
Google Scholar
[12] Florencio J, Sá Barreto F C 1999 Phys. Rev. B 60 9555
Google Scholar
[13] Chen S X, Shen Y Y, Kong X M 2010 Phys. Rev. B 82 174404
Google Scholar
[14] Da Conceição C M S, Maia R N P 2017 Phys. Rev. E 96 032121
[15] von Ohr S, Manssen M, Hartmann A K 2017 Phys. Rev. E 96 013315
Google Scholar
[16] Liu Z Q, Kong X M, Chen X S 2006 Phys. Rev. B 73 224412
Google Scholar
[17] Theodorakis P E, Georgiou I, Fytas N G 2013 Phys. Rev. E 87 032119
Google Scholar
[18] Crokidakis N, Nobre F D 2008 J. Phys. Condens. Matter 20 145211
Google Scholar
[19] Liu Z Q, Jiang S R, Kong X M 2014 Chin. Phys. B 23 087505
Google Scholar
[20] Hadjiagapiou I A 2011 Physica A 390 2229
Google Scholar
[21] Hadjiagapiou I A, Velonakis I N 2018 Physica A 505 965
Google Scholar
[22] Hadjiagapiou I A, Velonakis I N 2021 Physica A 578 126112
Google Scholar
[23] Kaufman M, Klunzinger P E, Khurana A 1986 Phys. Rev. B 34 4766
Google Scholar
[24] Saxena V K 1987 Phys. Rev. B 35 2055
Google Scholar
[25] Hadjiagapiou I A, Velonakis I N 2019 Physica A 534 122065
Google Scholar
[26] Mattis D C 1985 Phys. Rev. Lett. 55 3009
Google Scholar
[27] Sebastianes R M, Saxena V K 1987 Phys. Rev. B 35 2058
Google Scholar
[28] Fogedby H C 1978 J. Phys. C Solid State Phys. 11 2801
Google Scholar
[29] Kopeć T K, Usadel K D, Büttner G 1989 Phys. Rev. B 39 12418
Google Scholar
[30] Ovchinnikov A A, Dmitriev D V, Krivnov V Y, Cheranovskii V O 2003 Phys. Rev. B 68 214406
Google Scholar
[31] Yuan X J, Zhao J F, Wang H, Bu H X, Yuan H M, Zhao B Y, Kong X M 2021 Physica A 583 126279
Google Scholar
[32] Viswanath V S, Müller G 1994 The Recursion Method—Application to Many-body Dynamics (Berlin: Springe-Verlag)
[33] Mezei F, Murani A P 1979 J. Magn. Magn. Mater. 14 211
Google Scholar
[34] Lee M H 1982 Phys. Rev. Lett. 49 1072
Google Scholar
[35] Lee M H 1982 Phys. Rev. B 26 2547
Google Scholar
[36] Lee M H 2000 Phys. Rev. E 62 1769
Google Scholar
[37] Florencio J, De Alcantara Bonfim O F 2020 Front. Phys. 8 557277
Google Scholar
[38] 袁晓娟, 王辉, 赵邦宇, 赵敬芬, 明静, 耿延雷, 张凯煜 2021 70 197501
Google Scholar
Yuan X J, Wang H, Zhao B Y, Zhao J F, Ming J, Geng Y L, Zhang K Y 2021 Acta Phys. Sin. 70 197501
Google Scholar
-
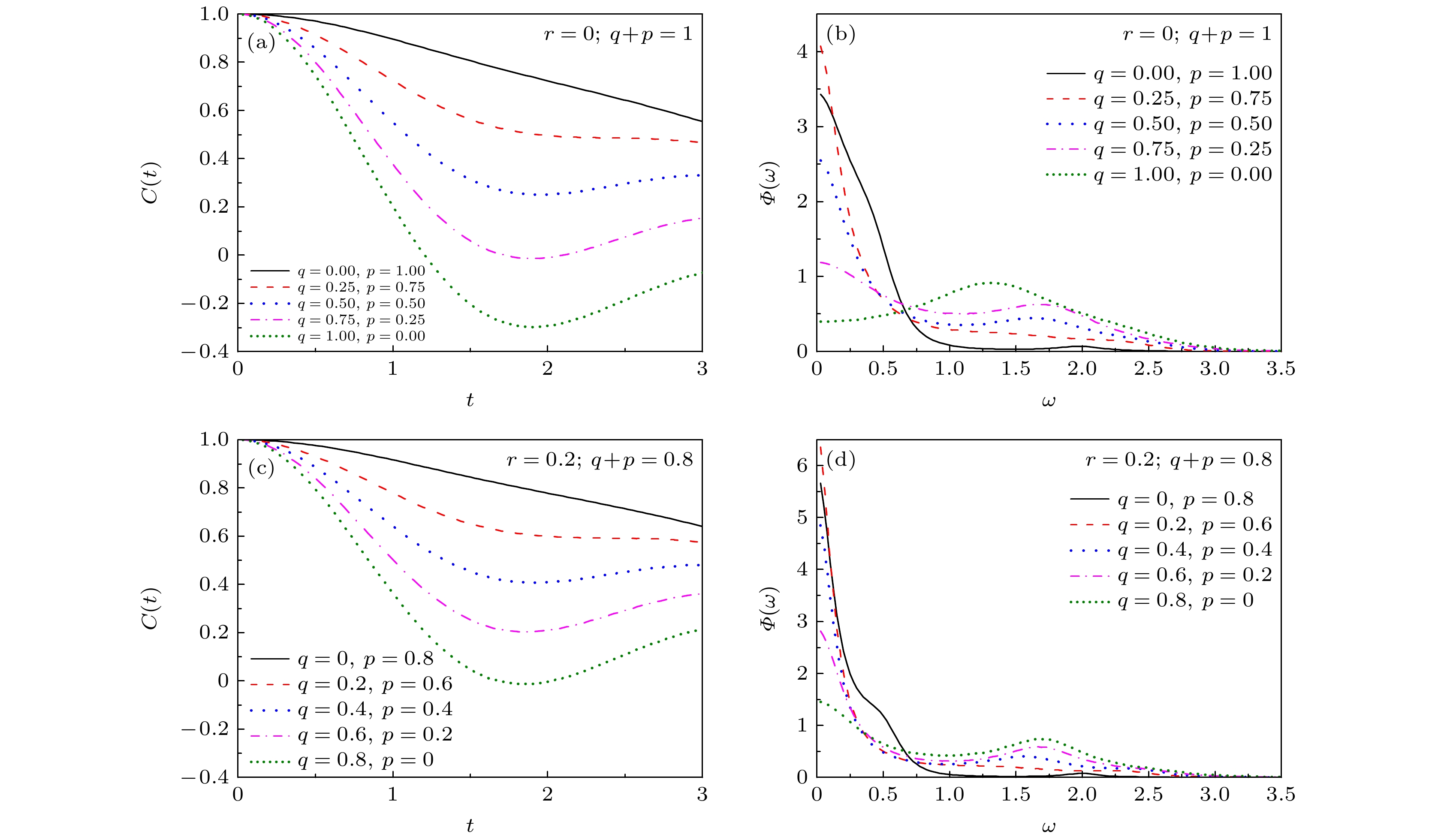
图 1 (a), (b)
$ r \equiv 0 $ 时的自旋关联函数$C\left( t \right)$ 及相应的谱密度$ \varPhi \left( \omega \right) $ ; (c), (d)$ r = 0.2 $ 时的$C\left( t \right)$ 及$ \varPhi \left( \omega \right) $ . 三模分布中的参数$ {B_p} = 0.5 $ ,$ {B_q} = 1.5 $ Figure 1. The spin autocorrelation function
$C\left( t \right)$ and corresponding spectral density$ \varPhi \left( \omega \right) $ for$ r \equiv 0 $ are given in graphs (a) and (b), and for$ r = 0.2 $ are given in graphs (c) and (d), respectively. The parameters$ {B_p} $ and$ {B_q} $ in the tri-modal distribution are 0.5 and 1.5, respectively.
图 2 (a)—(d)分别为系数
$ r = 0.4 $ , 0.6, 0.8, 0.96时的谱密度, 三模分布中的参数$ {B_p} = 0.5 $ ,$ {B_q} = 1.5 $ Figure 2. The spectral densities for
$ r = 0.4 $ , 0.6, 0.8 and 0.96 are given in (a)–(d), respectively. The parameters$ {B_p} $ and$ {B_q} $ in the tri-modal distribution are 0.5 and 1.5, respectively.
图 3 随机选取几组参数, 给出不同参数下的谱密度 (a)
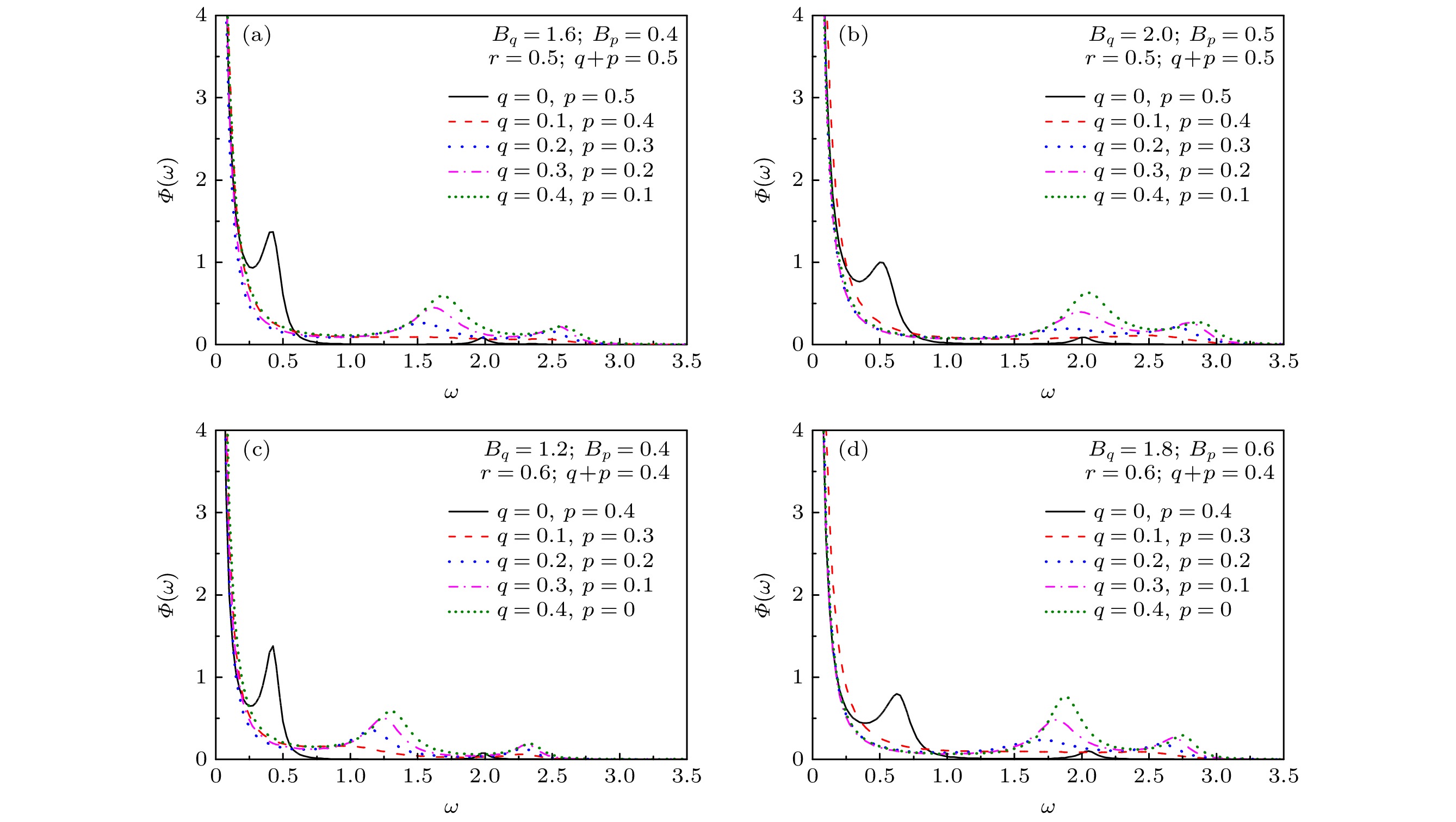
$ r = 0.5 $ ,$ {B_q} = 1.6 $ ,$ {B_p} = 0.4 $ ; (b)$ r = 0.5 $ ,$ {B_q} = 2.0 $ ,$ {B_p} = 0.5 $ ; (c)$ r = 0.6 $ ,$ {B_q} = 1.2 $ ,$ {B_p} = 0.4 $ ; (d)$ r = 0.6 $ ,$ {B_q} = 1.8 $ ,$ {B_p} = 0.6 $ . (a)—(d) 中红色虚线对应的参数满足$ q{B_q} = p{B_p} $ Figure 3. The spectral densities for several groups of parameters: (a)
$ r = 0.5 $ ,$ {B_q} = 1.6 $ ,$ {B_p} = 0.4 $ ; (b)$ r = 0.5 $ ,$ {B_q} = 2.0 $ ,$ {B_p} = 0.5 $ ; (c)$ r = 0.6 $ ,$ {B_q} = 1.2 $ ,$ {B_p} = 0.4 $ ; (d)$ r = 0.6 $ ,$ {B_q} = 1.8 $ ,$ {B_p} = 0.6 $ . The parameters corresponding to the red dashed lines in graphs (a)–(d) satisfy$ q{B_q} = p{B_p} $ .
图 4 (a)图3(c)所给参数下的连分式系数
${\varDelta _1}, {\varDelta _2}, \cdots , {\varDelta _9}$ , 仅给出了$ q \ne 0 $ 且$ p \ne 0 $ 时的结果, 参数取值为$ r = 0.6 $ ,$ {B_q} = 1.2 $ ,$ {B_p} = 0.4 $ ; (b)—(d)$ q = 0.1 $ , 0.2, 0.3时连分式系数线性拟合的结果Figure 4. (a) The first nine recurrents
${\varDelta _1}, {\varDelta _2}, \cdots , {\varDelta _9}$ for the parameters$ r = 0.6 $ ,$ {B_q} = 1.2 $ and$ {B_p} = 0.4 $ given in Fig. 3(c); (b)–(d) the linear fit results of the recurrents for$ q = 0.1 $ , 0.2 and 0.3, respectively.
图 5 三模型随机纵场蜕化为双模型随机纵场时的谱密度和自旋关联函数(插图), 三模分布系数
$ r = 0 $ , 参数$ {B_p} = 0.5 $ ,$ {B_q} = 1.5 $ Figure 5. Spectral density and spin autocorrelation function for trimodal-type random longitudinal magnetic field when
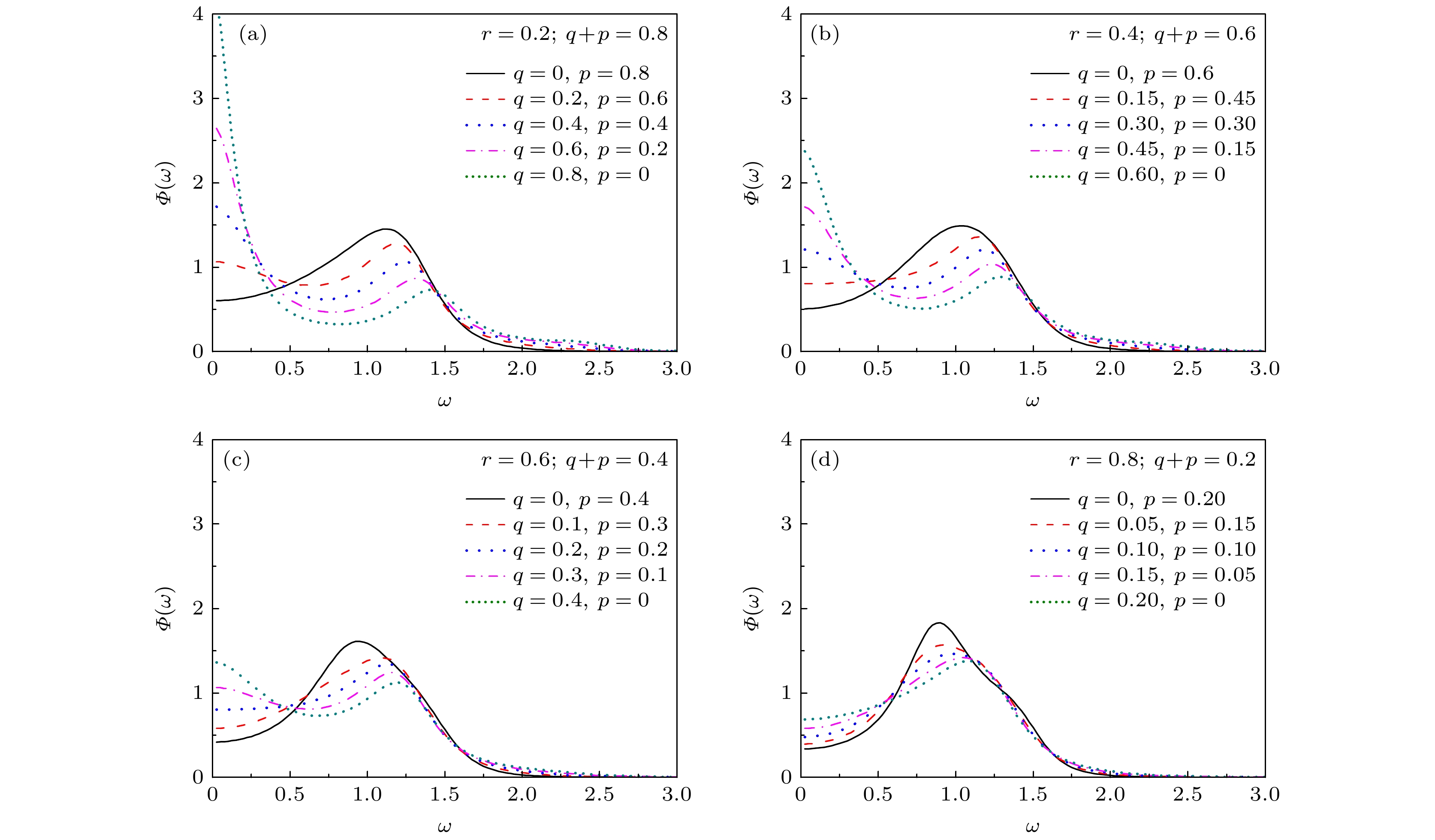
$ r = 0 $ . The inset is the corresponding result of$C\left( t \right)$ . The parameters$ {B_p} $ and$ {B_q} $ in the tri-modal distribution are 0.5 and 1.5, respectively.
图 6 随机纵场满足三模分布时的谱密度 (a)—(d)系数
$ r = 0.2 $ , 0.4, 0.6, 0.8. 三模分布中的参数$ {B_p} = 0.5 $ ,$ {B_q} = 1.5 $ Figure 6. Spectral densities for tri-modal-type random longitudinal magnetic field: (a)–(d)
$ r = 0.2 $ , 0.4, 0.6, 0.8. The parameters$ {B_p} $ and$ {B_q} $ in the tri-modal distribution are 0.5 and 1.5, respectively. -
[1] Kenzelmann M, Coldea R, Tennant D A, Visser D, Hofmann M, Smeibidl P, Tylczynski Z 2002 Phys. Rev. B 65 144432
Google Scholar
[2] Zhao Z Y, Liu X G, He Z Z, Wang X M, Fan C, Ke W P, Li Q J, Chen L M, Zhao X, Sun X F 2012 Phys. Rev. B 85 134412
Google Scholar
[3] Cui Y, Zou H, Xi N, He Z, Yang Y X, Shu L, Zhang G H, Hu Z, Chen T, Yu R, Wu J and Yu W 2019 Phys. Rev. Lett. 123 067203
Google Scholar
[4] Simon J, Bakr W S, Ma R, Tai M E, Preiss P M, Greiner M 2011 Nature 472 307
Google Scholar
[5] Dmitriev D V, Krivnov V Y 2004 Phys. Rev. B 70 144414
Google Scholar
[6] Neto M A, De Sousa J R 2013 Physica A 392 1
Google Scholar
[7] Corrêa Silva E V, Skea J E F, Rojas O, De Souza S M, Thomaz M T 2008 Physica A 387 5117
Google Scholar
[8] Do Nascimento D A, Neto M A, De Sousa J R, Pacobahyba J T 2012 J. Magn. Magn. Mater. 324 2429
Google Scholar
[9] Do Nascimento D A, Pacobahyba J T, Neto M A, Salmon O D R, Plascak J A 2017 Physica A 474 224
Google Scholar
[10] Senthil T 1998 Phys. Rev. B 57 8375
Google Scholar
[11] Liu Z Q, Jiang S R, Kong X M, Xu Y L 2017 Physica A 473 536
Google Scholar
[12] Florencio J, Sá Barreto F C 1999 Phys. Rev. B 60 9555
Google Scholar
[13] Chen S X, Shen Y Y, Kong X M 2010 Phys. Rev. B 82 174404
Google Scholar
[14] Da Conceição C M S, Maia R N P 2017 Phys. Rev. E 96 032121
[15] von Ohr S, Manssen M, Hartmann A K 2017 Phys. Rev. E 96 013315
Google Scholar
[16] Liu Z Q, Kong X M, Chen X S 2006 Phys. Rev. B 73 224412
Google Scholar
[17] Theodorakis P E, Georgiou I, Fytas N G 2013 Phys. Rev. E 87 032119
Google Scholar
[18] Crokidakis N, Nobre F D 2008 J. Phys. Condens. Matter 20 145211
Google Scholar
[19] Liu Z Q, Jiang S R, Kong X M 2014 Chin. Phys. B 23 087505
Google Scholar
[20] Hadjiagapiou I A 2011 Physica A 390 2229
Google Scholar
[21] Hadjiagapiou I A, Velonakis I N 2018 Physica A 505 965
Google Scholar
[22] Hadjiagapiou I A, Velonakis I N 2021 Physica A 578 126112
Google Scholar
[23] Kaufman M, Klunzinger P E, Khurana A 1986 Phys. Rev. B 34 4766
Google Scholar
[24] Saxena V K 1987 Phys. Rev. B 35 2055
Google Scholar
[25] Hadjiagapiou I A, Velonakis I N 2019 Physica A 534 122065
Google Scholar
[26] Mattis D C 1985 Phys. Rev. Lett. 55 3009
Google Scholar
[27] Sebastianes R M, Saxena V K 1987 Phys. Rev. B 35 2058
Google Scholar
[28] Fogedby H C 1978 J. Phys. C Solid State Phys. 11 2801
Google Scholar
[29] Kopeć T K, Usadel K D, Büttner G 1989 Phys. Rev. B 39 12418
Google Scholar
[30] Ovchinnikov A A, Dmitriev D V, Krivnov V Y, Cheranovskii V O 2003 Phys. Rev. B 68 214406
Google Scholar
[31] Yuan X J, Zhao J F, Wang H, Bu H X, Yuan H M, Zhao B Y, Kong X M 2021 Physica A 583 126279
Google Scholar
[32] Viswanath V S, Müller G 1994 The Recursion Method—Application to Many-body Dynamics (Berlin: Springe-Verlag)
[33] Mezei F, Murani A P 1979 J. Magn. Magn. Mater. 14 211
Google Scholar
[34] Lee M H 1982 Phys. Rev. Lett. 49 1072
Google Scholar
[35] Lee M H 1982 Phys. Rev. B 26 2547
Google Scholar
[36] Lee M H 2000 Phys. Rev. E 62 1769
Google Scholar
[37] Florencio J, De Alcantara Bonfim O F 2020 Front. Phys. 8 557277
Google Scholar
[38] 袁晓娟, 王辉, 赵邦宇, 赵敬芬, 明静, 耿延雷, 张凯煜 2021 70 197501
Google Scholar
Yuan X J, Wang H, Zhao B Y, Zhao J F, Ming J, Geng Y L, Zhang K Y 2021 Acta Phys. Sin. 70 197501
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 3012
- PDF Downloads: 79
- Cited By: 0
