-
We study the entanglement dynamics of the three-qubit Dicke model by means of the adiabatic approximation and the exact diagonalization in the parameter regime where the qubit transition frequencies are far off-resonance with the radiation field and the interaction strengths reach the ultrastrong-coupling regime. The single-mode field is prepared in the coherent state and two typical states GHZ and W are chosen as the initial three-qubit states. In the process of evolution, the interaction between the quantized field and three-qubit system leads to the generation of entanglement between the field and qubits, as well as between different parties in the three-qubit system, i.e. the pairwise entanglement of two qubits and the tripartite entanglement, which are of ongoing interest in quantum information process. The generalized concurrence and negativity are adopted to quantify different kinds of entanglement. The qubit-field entanglement never reaches the maximum and no sudden death occurs in the the tripartite entanglement for GHZ state, but it is exactly the opposite for W state. This reflects that the tripartite entanglement of the GHZ state is more robust than W sate, which is the same as in the rotating wave approximation. The results beyond the rotating wave approximation show that the pairwise entanglement gradually decreases and vanishes in the evolution of both initial states, with the tripartite entanglement periodically reaching relatively high level. This means that the interaction in system supports the tripartite entanglement at the cost of pairwise entanglement. The conclusions provide theoretical reference for the robustness of entanglement state and quantum information processing using Dicke model.
[1] Forn-Díaz P, Lamata L, Rico E, Kono J, Solano E 2019 Rev. Mod. Phys. 91 025005
Google Scholar
[2] Ciuti C, Bastard G, Carusotto I 2005 Phys. Rev. B 72 115303
Google Scholar
[3] Wallraffff A, Schuster D I, Blais A, Frunzio L, Huang R S, Majer J, Kumar S, Girvin S M, Schoelkopf R J 2004 Nature (London) 431 162
Google Scholar
[4] Blais A, Huang R S, Wallraffff A, Girvin S M, Schoelkopf R J 2004 Phys. Rev. A 69 062320
Google Scholar
[5] Gu X, Kockum A F, Miranowicz A, Liu Y X, Nori F 2017 Phys. Rep. 718 1
[6] Lv D, An S, Liu Z, Zhang J N, Pedernales J S, Lamata L, Solano E, Kim K 2018 Phys. Rev. X 8 021027
[7] Rabi I I 1936 Phys. Rev. 49 324
Google Scholar
[8] Braak D 2011 Phys. Rev. Lett. 107 100401
Google Scholar
[9] Liu T, Wang K L, Feng M 2009 Europhys. Lett. 86 54003
Google Scholar
[10] Chen Q H, Liu T, Zhang Y Y, Wang K L 2011 Europhys. Lett. 96 14003
Google Scholar
[11] He S, Wang C, Chen Q H, Ren X Z, Liu T, Wang K L 2012 Phys. Rev. A 86 033837
Google Scholar
[12] Chen Q H, Wang C, He S, Liu T, Wang K L 2012 Phys. Rev. A 86 023822
Google Scholar
[13] Hu B L, Zhou H L, Chen S J, Gao X L, Wang K L 2017 J. Phys. A: Math. Theor. 50 074004
Google Scholar
[14] Xie W J, Mao B B, Li G Z, Wang W H, Sun C, Wang Y M, You W L, Liu M X 2020 J. Phys. A: Math. Theor. 53 095302
Google Scholar
[15] 李志强, 王月明 2019 68 173201
Google Scholar
Li Z Q, Wang Y M 2019 Acta Phys. Sin. 68 173201
Google Scholar
[16] Dicke R H 1954 Phys. Rev. 93 99
Google Scholar
[17] Wang Y K, Hioe F T 1973 Phys. Rev. A 7 831
Google Scholar
[18] Emary C, Brandes T 2003 Phys. Rev. E 67 066203
Google Scholar
[19] Baumann K, Guerlin C, Brennecke F, Esslinger T 2010 Nature 464 1301
Google Scholar
[20] Kirton P, Roses M M, Keeling J, Dalla Torre E G 2019 Adv. Quantum Technol. 2 1800043
Google Scholar
[21] Alavirad Y, Lavasani A 2019 Phys. Rev. A 99 043602
Google Scholar
[22] Lewis-Swan R J, Safavi-Naini A, Bollinger J J, Rey A M 2019 Nat. Commun. 10 1581
Google Scholar
[23] Liu M X, Chesi S, Ying Z J, Chen X S, Luo H G, Lin H Q 2017 Phys. Rev. Lett. 119 220601
Google Scholar
[24] 程景, 单传家, 刘继兵, 黄燕霞, 刘堂昆 2018 67 110301
Google Scholar
Cheng J, Shan C J, Liu J B, Huang Y X, Liu T K 2018 Acta Phys. Sin. 67 110301
Google Scholar
[25] 左战春, 夏云杰 2003 52 2687
Google Scholar
Zuo Z C, Xia Y J 2003 Acta Phys. Sin. 52 2687
Google Scholar
[26] 郭亮, 梁先庭 2009 58 50
Google Scholar
Guo L, Liang X T 2009 Acta Phys. Sin. 58 50
Google Scholar
[27] 张国锋, 卜晶晶 2010 59 1462
Google Scholar
Zhang G F, Bu J J 2010 Acta Phys. Sin. 59 1462
Google Scholar
[28] Youssef M, Metwally N, Obada A S F 2010 J. Phys. B 43 095501
Google Scholar
[29] Zhang Y Y, Chen X Y, He S, Chen Q H 2016 Phys. Rev. A 94 012317
Google Scholar
[30] Badshah F, Ge G Q, Paternostro M, Qamar S 2020 J. Opt. Soc. Am. B 37 949
Google Scholar
[31] Mao L J, Liu Y X, Zhang Y B 2016 Phys. Rev. A 93 052305
Google Scholar
[32] Roderick M, Horodecki P, Horodecki R 1998 Phys. Rev. Lett. 80 5239
Google Scholar
[33] Coffman V, Kundu J, Wootters W K 2000 Phys. Rev. A 61 052306
Google Scholar
[34] Dür W, Vidal G, Cirac J 2000 Phys. Rev. A 62 062314
Google Scholar
[35] Ou Y C, Fan H 2007 Phys. Rev. A 75 062308
Google Scholar
[36] Dukalski M, Blanter Y M 2013 arXiv 1301.4857
[37] Agarwal S, Hashemi Rafsanjani S M, Eberly J H 2012 Phys. Rev. A 85 043815
Google Scholar
[38] Rungta P, Bužek V, Caves C M, Hillery M, Milburn G J 2001 Phys. Rev. A 64 042315
Google Scholar
[39] Wootters W K 1998 Phys. Rev. Lett. 80 2245
Google Scholar
[40] Zyczkowski K, Horodecki P, Sanpera A, Lewenstein M 1998 Phys. Rev. A 58 883
Google Scholar
-
图 1 初始时刻为GHZ态(左)和W态(右)时,
$\left(\rm i \right)$ 类两体纯态纠缠I tangle, 其中红色(实线)表示数值结果, 蓝色(虚线)表示解析结果, 系统参数为$ \omega = 0.15{\omega _{\rm{c}}}$ ,$ z = 3$ ,$g = 0.02{\omega _{\rm{c}}}~\left( {\rm{a}} \right)$ ,$0.04{\omega _{\rm{c}}}~\left(\rm b \right)$ ,$0.06{\omega _{\rm{c}}}~\left(\rm c \right)$ ,$0.08{\omega _{\rm{c}}}~\left(\rm d \right)$ Figure 1. Time evolution of the I tangle for the type
$\left( \rm i \right)$ with the initial GHZ (left) and W (right) states for$\omega = 0.15{\omega _{\rm{c}}}$ ,$z = 3$ , and different coupling strengths:$g = 0.02{\omega _{\rm{c}}}~\left(\rm a \right)$ ,$0.04{\omega _{\rm{c}}}~\left(\rm b \right)$ ,$0.06{\omega _{\rm{c}}}~\left(\rm c \right)$ ,$0.08{\omega _{\rm{c}}}~\left(\rm d \right)$ , given by the numerical method (solid red line), and the analytical approach (dashed blue line).
图 2 初始时刻为GHZ态(左)和W态(右)时,
$\left( {\rm ii} \right)$ 类两体纯态I tangle随时间的演化, 其中红色(实线)表示数值结果, 蓝色(虚线)表示解析结果, 系统参数与图1相同Figure 2. Time evolution of the I tangle for the type
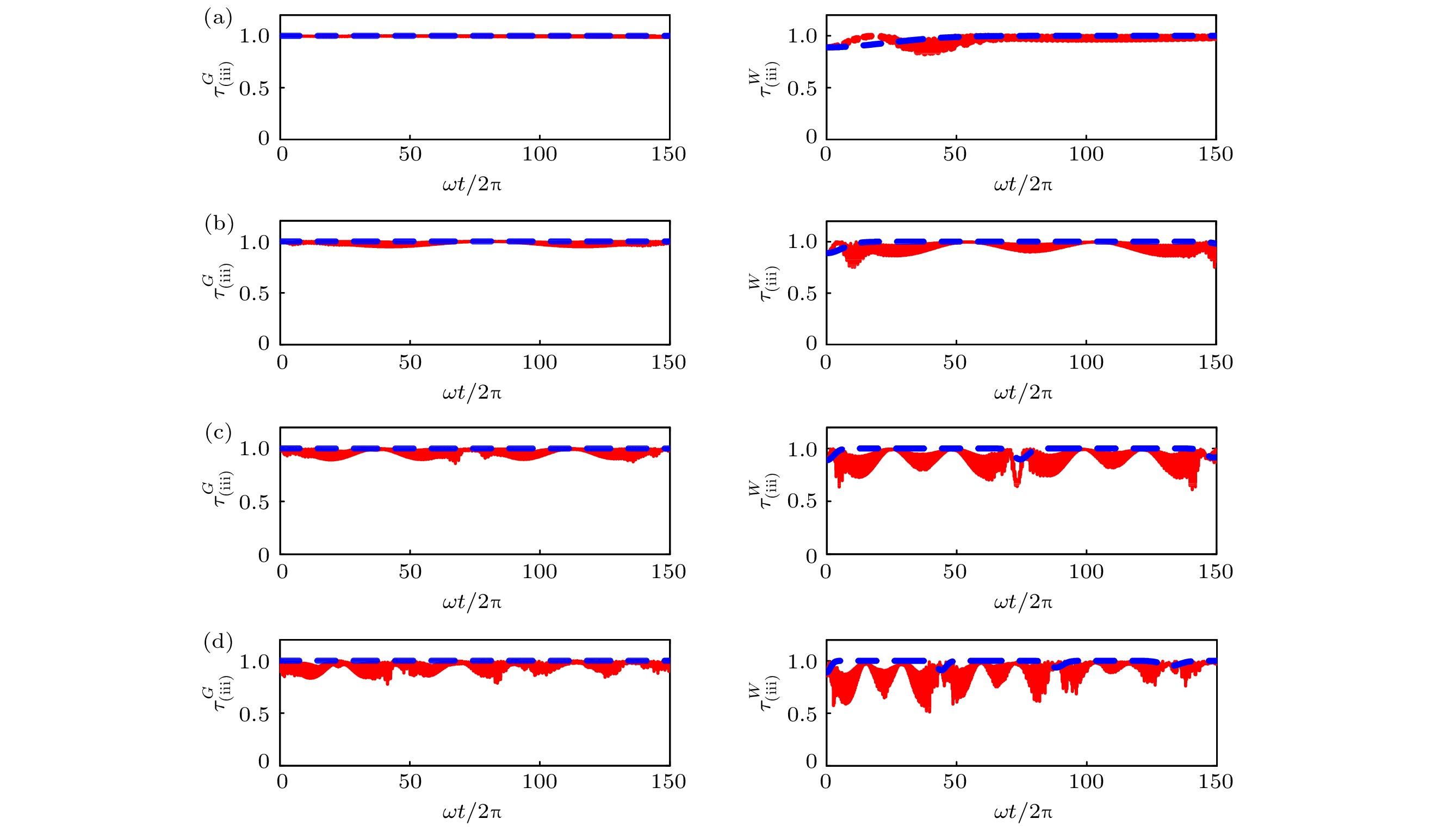
$\left( {\rm ii} \right)$ with the initial GHZ (left) and W (right) given by the numerical method (solid red line), and the analytical approach (dashed blue line). The corresponding parameters are the same as in Fig. 1.
图 3 初始时刻为GHZ态(左)和W态(右)时, (iii) 类两体纯态I tangle随时间的演化, 其中红色(实线)表示数值结果, 蓝色(虚线)表示解析结果, 系统参数与图1相同
Figure 3. Time evolution of the I tangle for the type (iii) with the initial GHZ (left) and W (right) states given by the numerical method (solid red line), and the analytical approach (dashed blue line). The corresponding parameters are the same as in Fig. 1.
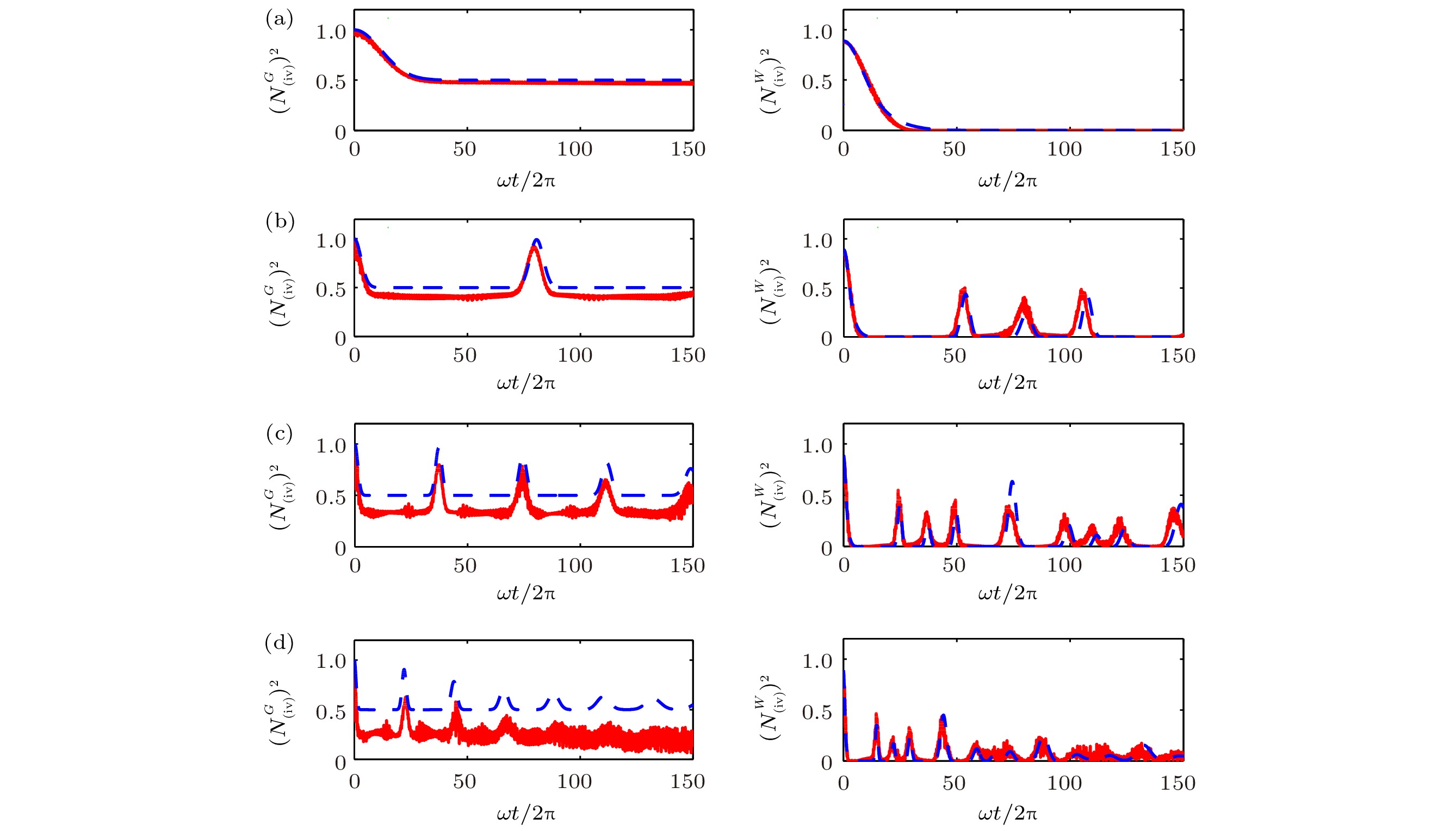
图 4 初始时刻为GHZ(左)态和W(右)态时, (iv)类纠缠负值度的平方随时间的演化, 其中红色(实线)表示数值结果, 蓝色(虚线)表示解析结果, 系统参数与图1相同
Figure 4. Time evolution of the square of the negativity for the type (iv) with the initial GHZ (left) and W (right) given by the numerical method (solid red line), and the analytical approach (dashed blue line). The corresponding parameters are the same as in Fig. 1.
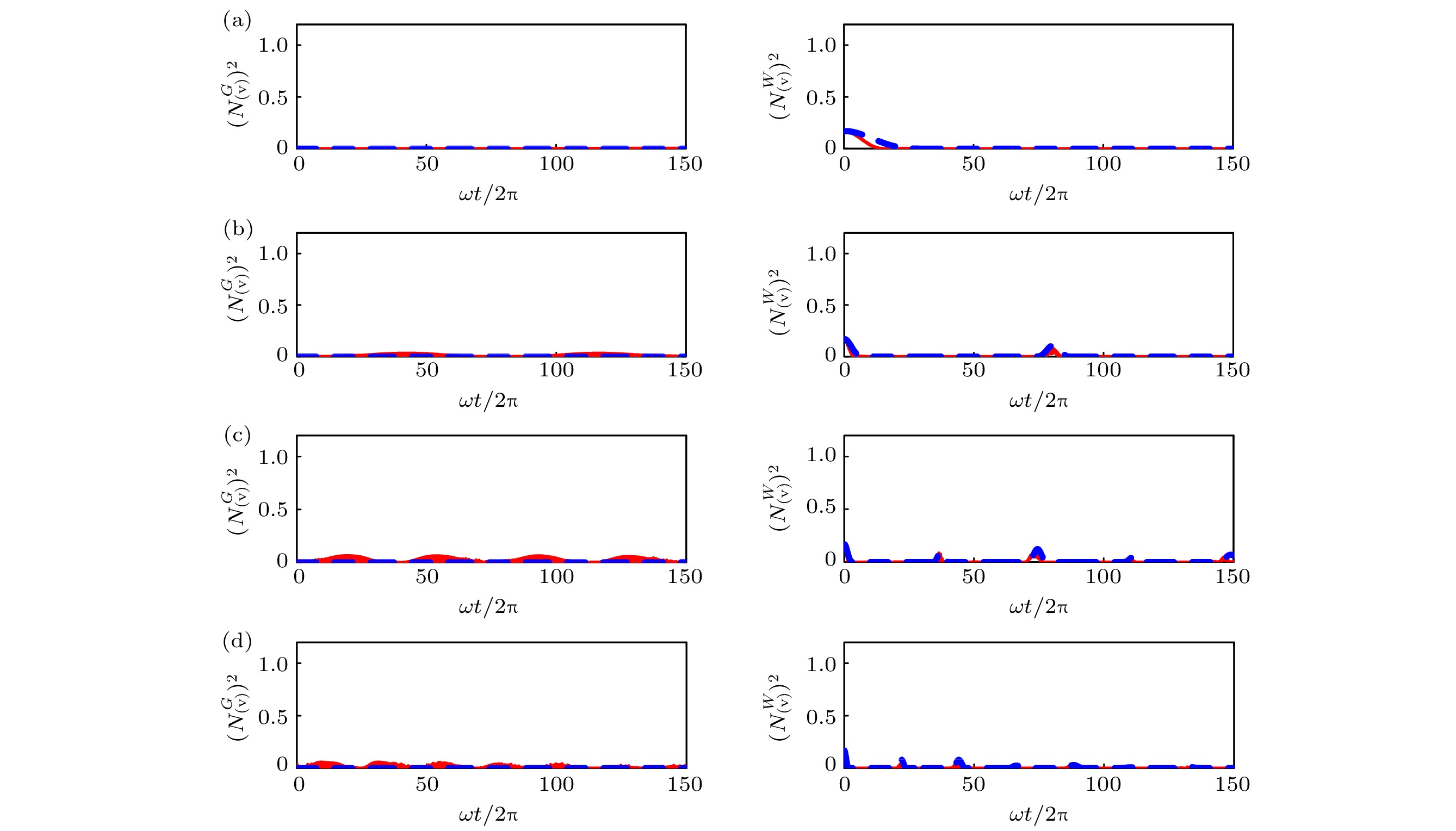
图 5 初始时刻为GHZ(左)态和W(右)态时, (v) 类对纠缠负值度的平方随时间的演化, 其中红色(实线)表示数值结果, 蓝色(虚线)表示解析结果, 系统参数与图1相同
Figure 5. Time evolution of the square of the negativity for the type (v) with the initial GHZ (left) and W (right) given by the numerical method (solid red line), and the analytical approach (dashed blue line). The corresponding parameters are the same as in Fig. 1.
图 6 初始时刻为GHZ(左)态和W(右)态时, 真正的三体纠缠π-tangle随时间的演化, 其中红色(实线)表示数值结果, 绿色(实线)表示绝热近似结果, 蓝色(虚线)表示解析结果, 系统参数与图1相同
Figure 6. Time evolution of π-tanglewith the initial GHZ (left) and W (right) given by the numerical method (solid red line), the adiabatic approximation method (solid green line) and the analytical approach (dashed blue line). The corresponding parameters are the same as in Fig. 1.
-
[1] Forn-Díaz P, Lamata L, Rico E, Kono J, Solano E 2019 Rev. Mod. Phys. 91 025005
Google Scholar
[2] Ciuti C, Bastard G, Carusotto I 2005 Phys. Rev. B 72 115303
Google Scholar
[3] Wallraffff A, Schuster D I, Blais A, Frunzio L, Huang R S, Majer J, Kumar S, Girvin S M, Schoelkopf R J 2004 Nature (London) 431 162
Google Scholar
[4] Blais A, Huang R S, Wallraffff A, Girvin S M, Schoelkopf R J 2004 Phys. Rev. A 69 062320
Google Scholar
[5] Gu X, Kockum A F, Miranowicz A, Liu Y X, Nori F 2017 Phys. Rep. 718 1
[6] Lv D, An S, Liu Z, Zhang J N, Pedernales J S, Lamata L, Solano E, Kim K 2018 Phys. Rev. X 8 021027
[7] Rabi I I 1936 Phys. Rev. 49 324
Google Scholar
[8] Braak D 2011 Phys. Rev. Lett. 107 100401
Google Scholar
[9] Liu T, Wang K L, Feng M 2009 Europhys. Lett. 86 54003
Google Scholar
[10] Chen Q H, Liu T, Zhang Y Y, Wang K L 2011 Europhys. Lett. 96 14003
Google Scholar
[11] He S, Wang C, Chen Q H, Ren X Z, Liu T, Wang K L 2012 Phys. Rev. A 86 033837
Google Scholar
[12] Chen Q H, Wang C, He S, Liu T, Wang K L 2012 Phys. Rev. A 86 023822
Google Scholar
[13] Hu B L, Zhou H L, Chen S J, Gao X L, Wang K L 2017 J. Phys. A: Math. Theor. 50 074004
Google Scholar
[14] Xie W J, Mao B B, Li G Z, Wang W H, Sun C, Wang Y M, You W L, Liu M X 2020 J. Phys. A: Math. Theor. 53 095302
Google Scholar
[15] 李志强, 王月明 2019 68 173201
Google Scholar
Li Z Q, Wang Y M 2019 Acta Phys. Sin. 68 173201
Google Scholar
[16] Dicke R H 1954 Phys. Rev. 93 99
Google Scholar
[17] Wang Y K, Hioe F T 1973 Phys. Rev. A 7 831
Google Scholar
[18] Emary C, Brandes T 2003 Phys. Rev. E 67 066203
Google Scholar
[19] Baumann K, Guerlin C, Brennecke F, Esslinger T 2010 Nature 464 1301
Google Scholar
[20] Kirton P, Roses M M, Keeling J, Dalla Torre E G 2019 Adv. Quantum Technol. 2 1800043
Google Scholar
[21] Alavirad Y, Lavasani A 2019 Phys. Rev. A 99 043602
Google Scholar
[22] Lewis-Swan R J, Safavi-Naini A, Bollinger J J, Rey A M 2019 Nat. Commun. 10 1581
Google Scholar
[23] Liu M X, Chesi S, Ying Z J, Chen X S, Luo H G, Lin H Q 2017 Phys. Rev. Lett. 119 220601
Google Scholar
[24] 程景, 单传家, 刘继兵, 黄燕霞, 刘堂昆 2018 67 110301
Google Scholar
Cheng J, Shan C J, Liu J B, Huang Y X, Liu T K 2018 Acta Phys. Sin. 67 110301
Google Scholar
[25] 左战春, 夏云杰 2003 52 2687
Google Scholar
Zuo Z C, Xia Y J 2003 Acta Phys. Sin. 52 2687
Google Scholar
[26] 郭亮, 梁先庭 2009 58 50
Google Scholar
Guo L, Liang X T 2009 Acta Phys. Sin. 58 50
Google Scholar
[27] 张国锋, 卜晶晶 2010 59 1462
Google Scholar
Zhang G F, Bu J J 2010 Acta Phys. Sin. 59 1462
Google Scholar
[28] Youssef M, Metwally N, Obada A S F 2010 J. Phys. B 43 095501
Google Scholar
[29] Zhang Y Y, Chen X Y, He S, Chen Q H 2016 Phys. Rev. A 94 012317
Google Scholar
[30] Badshah F, Ge G Q, Paternostro M, Qamar S 2020 J. Opt. Soc. Am. B 37 949
Google Scholar
[31] Mao L J, Liu Y X, Zhang Y B 2016 Phys. Rev. A 93 052305
Google Scholar
[32] Roderick M, Horodecki P, Horodecki R 1998 Phys. Rev. Lett. 80 5239
Google Scholar
[33] Coffman V, Kundu J, Wootters W K 2000 Phys. Rev. A 61 052306
Google Scholar
[34] Dür W, Vidal G, Cirac J 2000 Phys. Rev. A 62 062314
Google Scholar
[35] Ou Y C, Fan H 2007 Phys. Rev. A 75 062308
Google Scholar
[36] Dukalski M, Blanter Y M 2013 arXiv 1301.4857
[37] Agarwal S, Hashemi Rafsanjani S M, Eberly J H 2012 Phys. Rev. A 85 043815
Google Scholar
[38] Rungta P, Bužek V, Caves C M, Hillery M, Milburn G J 2001 Phys. Rev. A 64 042315
Google Scholar
[39] Wootters W K 1998 Phys. Rev. Lett. 80 2245
Google Scholar
[40] Zyczkowski K, Horodecki P, Sanpera A, Lewenstein M 1998 Phys. Rev. A 58 883
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 6190
- PDF Downloads: 138
- Cited By: 0
