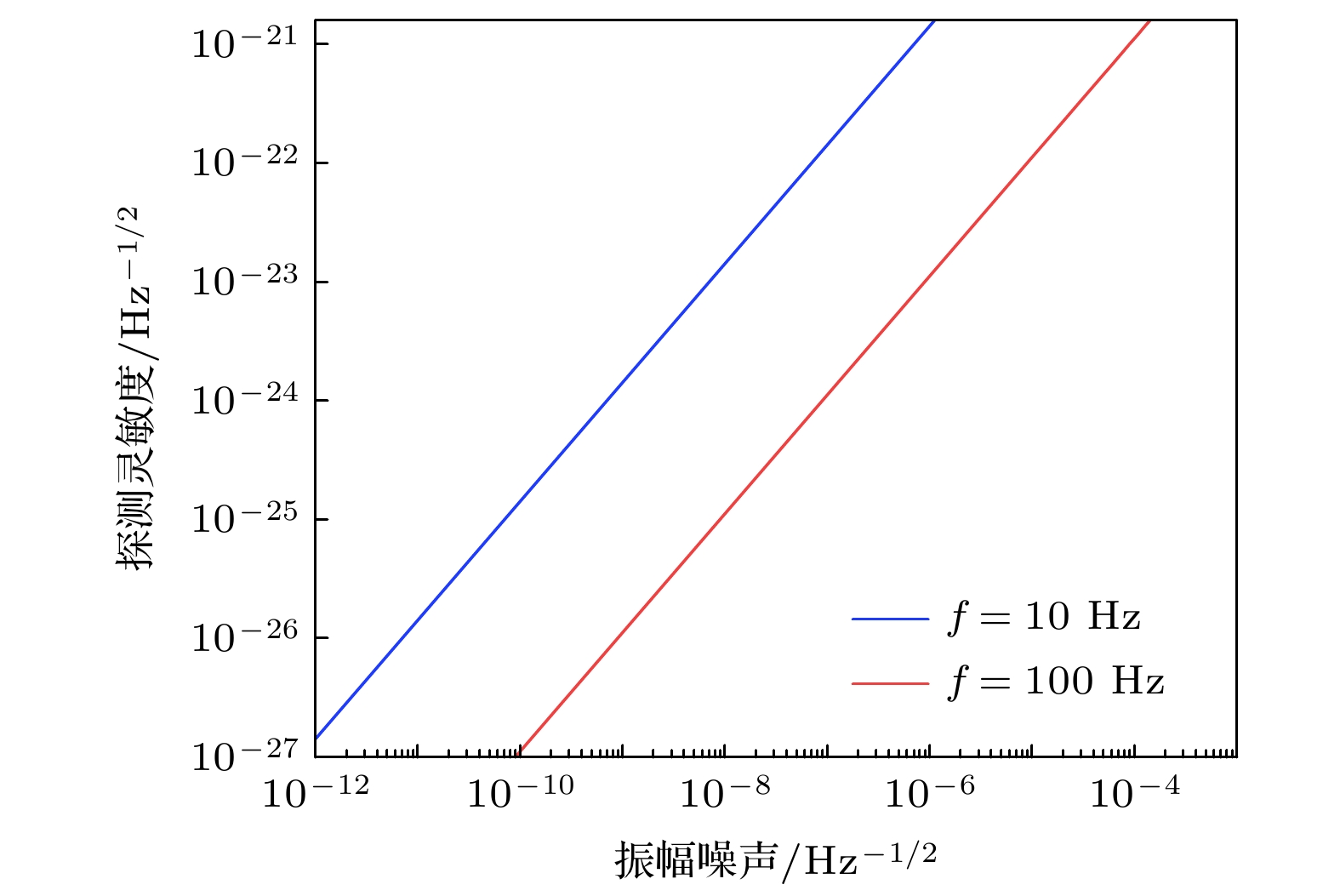
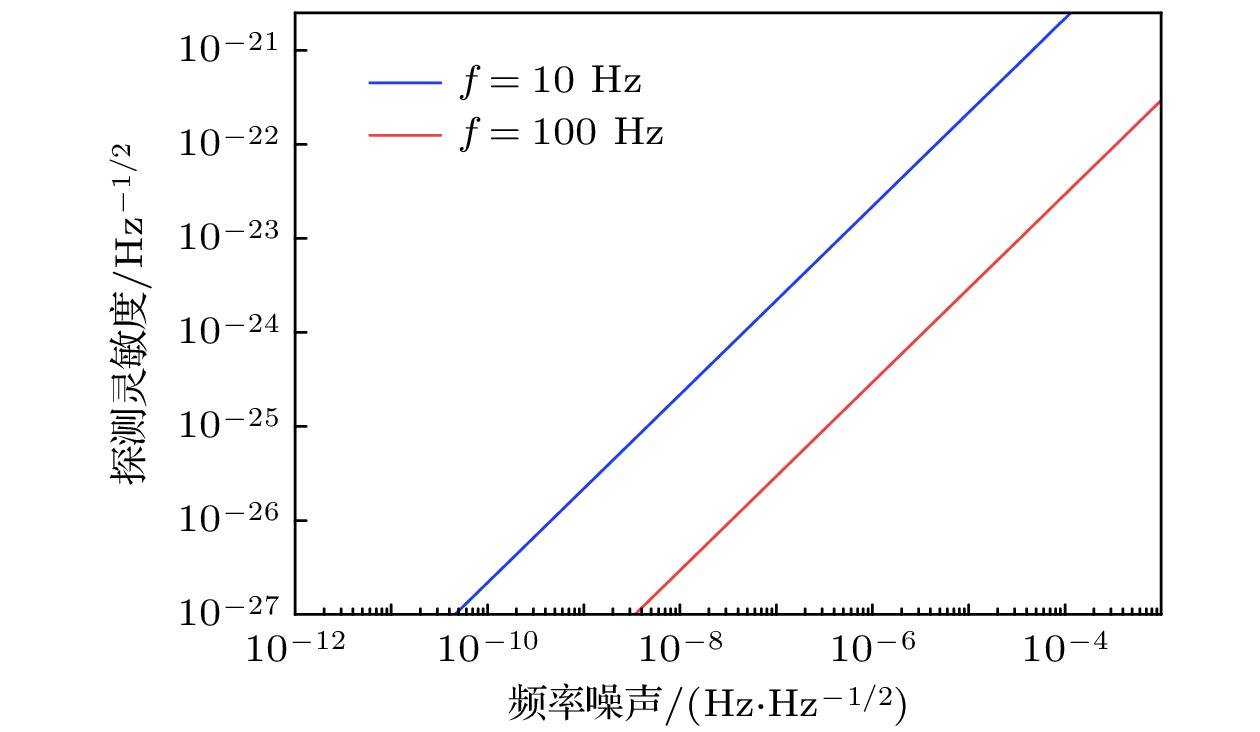
-
Gravitational waves (GWs), predicted by the general relativity of Albert Einstein, are ripples in space-time caused by massive accelerating objects. Since the first direct observation of GWs in 2015, more and more binary black hole mergers and neutron star merger were detected by the laser interferometer gravitational-wave observatory (LIGO) and the Virgo interferometric detector. The construction of the third-generation (3G) gravitational wave detector(GWD), whose sensitivity is ten times that of the second-generation (2G) GWD (Advanced LIGO and Virgo), can not only push the gravitational wave astronomy towards the edge of the observable universe, but also test the fundamental laws of physics and study the nature of matter. By utilizing the abandoned underground mines, Shanxi university proposes to construct a 3G ground-based gravitational wave detector with an arm length of 10 km and a strain sensitivity of 10–24 Hz–1/2, improving the location accuracy of wave source by participating in the global GWD network. The construction of 3G GWD has many technical challenges, including ultrahigh large-scale vacuum system, ultrastable seismic isolation system, high-precision control system, high-quality laser and quantum source. Theoretically, the sensitivity of GWD with equal arm length is not limited by the laser source noise. However, in the actual scenario, the sensitivity is limited by the differences in arm length, arm cavity linewidth, arm reflectivity, arm mass, arm power, and the laser parameters. In this work, based on the design sensitivity (10–24 Hz–1/2) of dual-recycled Fabry-Perot Michelson interferometer, we propose the requirements for an ultra low-noise laser, including wavelength, amplitude noise, frequency noise, beam pointing noise and fundamental mode purity. The results show that in order to achieve the design sensitivity at the Fourier frequency of 100 Hz, the wavelength of the laser source should be 1.5 μm, the output power should be higher than 200 W, the amplitude noise should be better than 10–8 Hz–1/2, and the frequency noise should be better than 100 Hz/Hz1/2. To achieve the sensitivity of 10–24 Hz–1/2 at 10 Hz analysis frequency, the requirements for the amplitude and frequency noise of the laser source are much more stringent. This study lays a solid foundation for the analysis of laser source noise and the decomposition of interferometer indexes .
-
Keywords:
- gravitational wave detection /
- strain sensitivity /
- low-noise laser /
- noise budget
[1] Abbott B P, Abbott R, Abbott T D, et al. 2016 Phys. Rev. Lett. 116 061102
Google Scholar
[2] Abbott B P, Abbott R, Abbott T D, et al. 2016 Phys. Rev. Lett. 116 241103
Google Scholar
[3] Vermeulen S M, Relton P, Grote H, et al. 2021 Nature 600 424
Google Scholar
[4] Bailes M, Berger B K, Brady P R, et al. 2021 Nat. Rev. Phys. 3 344
Google Scholar
[5] Abbott R, Abbott T D, Abraham S, et al. 2021 Astrophys. J. Lett. 915 L5
Google Scholar
[6] Badaracco F, Rossi C D, Fiori I, Harms J, Miyo K, Paoletti F, Tanaka T, Washimi T, Yokozawa T 2021 Phys. Rev. D 104 042006
Google Scholar
[7] Hall E D, Kuns K, Smith J R, et al. 2021 Phys. Rev. D 103 122004
Google Scholar
[8] Buikema A, Cahillane C, Mansell G L, et al. 2020 Phys. Rev. D 102 062003
Google Scholar
[9] Adhikari R X 2014 Rev. Mod. Phys. 86 121
Google Scholar
[10] Bond C, Brown D, Freise A, Strain K A 2016 Living Rev. Relativ. 19 3
Google Scholar
[11] Matichard F, Lantz B, Mittleman R, et al. 2015 Classical Quant. Grav. 32 185003
Google Scholar
[12] P. Nguyen, Schofield R M S, Effler A, et al. 2021 Classical Quant. Grav. 38 145001
Google Scholar
[13] Adhikari R X, Arai K, Brooks A F, et al. 2020 Classical Quant. Grav. 37 165003
Google Scholar
[14] Hammond G, Hild S, Pitkin M 2014 J. Mod. Optic. 61 S10
Google Scholar
[15] Heurs M 2018 Philos. T. R. Soc. A 376 20170289
Google Scholar
[16] Danilishin S L, Khalili F Y, Miao H 2019 Living Rev. Relativ. 22 2
Google Scholar
[17] Sigg D 1997 LIGO Report No. LIGO- T970084-00 D
[18] Rana A 2004 Ph. D. Dissertation (Cambridge: Massachusetts Institute of Technology)
[19] Somiya K, Chen Y 2006 Phys. Rev. D 73 122005
Google Scholar
[20] Izumi K, Sigg D, Kawabe K 2016 LIGO Report No. LIGO-T1500325
[21] Izumi K, Sigg D, Kawabe K 2016 LIGO Report No. LIGO-T1500461
[22] Izumi K, Sigg D, Kawabe K 2016 LIGO Report No. LIGO-T1500559
[23] Cahillane C 2021 Ph. D. Dissertation (Pasadena: California Institute of Technology)
[24] Cahillane C, Mansell G L, Sigg D 2021 Opt. Express 29 42144
Google Scholar
[25] Buonanno A, Chen Y 2001 Phys. Rev. D 64 042006
Google Scholar
[26] Pitkin M, Reid S, Rowan S, Hough J 2011 Living Rev. Relativ. 14 5
Google Scholar
[27] Kwee P 2010 Ph. D. Dissertation (Hanover: Wilhelm Leibniz University)
[28] Chen Z, Guo M, Zhang R, Zhou B, Wei Q 2018 Sensors 18 02603
Google Scholar
[29] Degallaix J, Komma J, Forest D, Hofmann G 2014 Classical Quant. Grav. 31 185010
Google Scholar
[30] Khalaidovski A, Steinlechner J, Schnabel R 2013 Classical Quant. Grav. 30 165001
Google Scholar
[31] Biscans S, Gras S, Blair C D, Driggers J, Evans M, Fritschel P, Hardwick T, Mansell G 2019 Phys. Rev. D 100 122003
Google Scholar
-
图 1 引力波探测器光路图
Figure 1. Diagram of the optical layout of Gravitational wave detection.
图 2 探测灵敏度与激光功率的关系图
Figure 2. Detection sensitivity as a function of laser power.
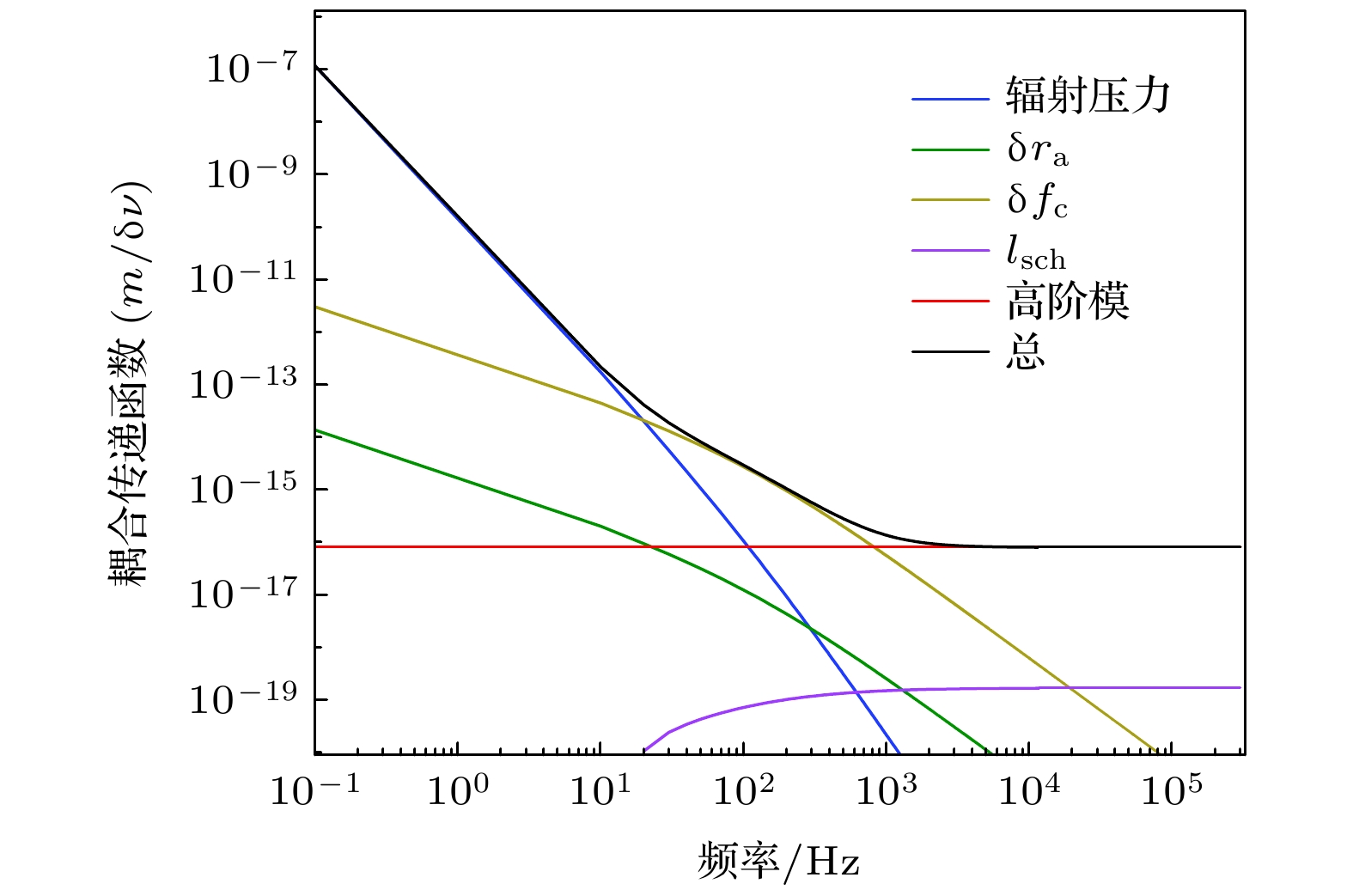
图 3 激光源振幅噪声耦合传递函数图 (a) DARM偏移、辐射压力差异和对比度缺陷引起的振幅噪声耦合; (b) 辐射压力差异引起的振幅噪声耦合
Figure 3. Coupling transfer function of laser amplitude noise: (a) Amplitude noise coupling due to DARM offset, radiation pressure difference and contrast defect; (b) amplitude noise coupling due to radiation pressure difference.
图 4 探测灵敏度与激光源振幅噪声关系图
Figure 4. Detection sensitivity as a function of laser amplitude noise.
图 5 激光频率噪声耦合传递函数图
Figure 5. Coupling transfer function of laser frequency noise.
图 6 探测灵敏度与激光源频率噪声关系图
Figure 6. Detection sensitivity as a function of laser frequency noise.
表 1 山西大学引力波探测干涉仪参数表
Table 1. Parameter of Shanxi University gravitation waves detection interferometer.
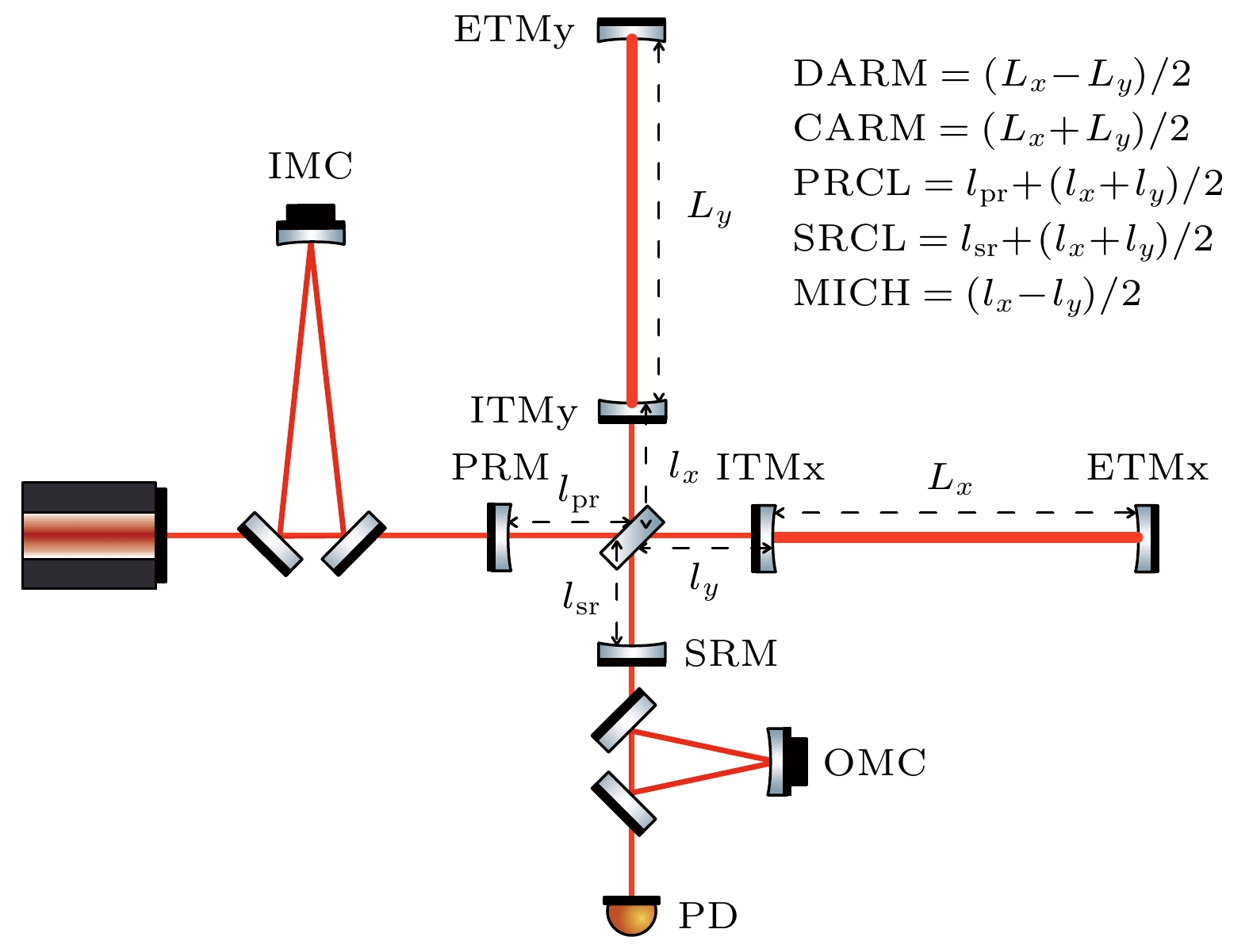
参数 符号表示 数值 臂长 $ L $ 10 km 激光波长 $ \lambda $ 1550 nm 激光频率 $ {\nu _0} $ 1.94 × 1014 Hz ITM, ETM质量 $ M $ 200 kg 约化质量 $ \mu = \dfrac{{{m_{\text{i}}}{m_{\text{e}}}}}{{{m_{\text{i}}} + {m_{\text{e}}}}} = \dfrac{M}{2} $ 100 kg $ \delta \mu = \dfrac{{{\mu _x} - {\mu _y}}}{2} $ –0.001 kg ITM透射率 $ t_{\text{i}}^{\text{2}} $ 1.4% ETM透射率 $ t_{\text{e}}^2 $ 5 × 10–6 PRM透射率 $ t_{\text{p}}^2 $ 3% SRM透射率 $ t_{\text{s}}^{\text{2}} $ 20% 激光功率 $ {P_{{\text{in}}}} $ 200 W 功率循环腔增益 $ g_{\text{p}}^2 = {\left( {\dfrac{{{t_{\text{p}}}}}{{1 - {r_{\text{p}}}{r_{\text{a}}}}}} \right)^2} $ 120 信号循环腔增益 $ g_{\text{s}}^{\text{2}} = {\left( {\dfrac{{{t_{\text{s}}}}}{{1 + {r_{\text{s}}}{r_{\text{a}}}}}} \right)^2} $ 0.06 臂腔增益 $ g_{{\text{arm}}}^{\text{2}} = {\left( {\dfrac{{{t_{\text{i}}}}}{{1 - {r_{\text{e}}}{r_{\text{i}}}}}} \right)^2} $ 284 臂腔反射率 $ {r_{\text{a}}} = \dfrac{{ - {r_{\text{i}}} + {r_{\text{e}}}}}{{1 - {r_{\text{i}}}{r_{\text{e}}}}} $ 0.99929 $ \delta {r_{\text{a}}} = \dfrac{{{r_{{\text{a}}x}} - {r_{{\text{a}}y}}}}{2} $ 31 × 10–6 反射率导数 $r_{\text{a} }' = \dfrac{ {t_{\text{i} }^{\text{2} }{r_{\text{e} } } }}{ { { {\left( {1 - {r_{\text{i} } }{r_{\text{e} } } } \right)}^2} } }$ 283.5 臂腔线宽 $ {f_c} = \dfrac{c}{{4{\text{π }}L}}\lg \left( {\dfrac{1}{{r_{\text{i}}^{\text{2}}r_{\text{e}}^{\text{2}}}}} \right) $ 14.6 Hz $ \delta {f_c} = \dfrac{{{f_{cx}} - {f_{cy}}}}{2} $ 0.05 Hz 臂腔精细度 $ F = \dfrac{{{\text{π }}\sqrt {{r_{\text{i}}}{r_{\text{e}}}} }}{{1 - {r_{\text{i}}}{r_{\text{e}}}}} $ 445.5 总损耗 $ T $ 2.24 % 臂腔功率 $ {P_{\text{a}}} = \dfrac{1}{2}{P_{{\text{laser}}}}g_{\text{p}}^{\text{2}}g_{{\text{arm}}}^2 $ 3.4 MW $ \delta {P_{\text{a}}} = \dfrac{{{P_{ax}} - {P_{ay}}}}{2} $ –6.5 kW CARM腔
线宽${f_{cc} } = \dfrac{c}{ {4{\text{π } }L} }\lg \left( {\dfrac{ {1 + {r_{\text{i} } }{r_{\text{p} } } }}{ { {r_{\text{i} } }{r_{\text{e} } } + {r_{\text{p} } }{r_{\text{e} } }\left( {t_{\text{i} }^{\text{2} } + r_{\text{i} }^{\text{2} } } \right)} } } \right)$ 0.06 Hz DARM腔
线宽$ {f_{{\text{rse}}}} = \dfrac{c}{{4{\text{π }}L}}\lg \left( {\dfrac{{1 - {r_{\text{i}}}{r_{\text{s}}}}}{{{r_{\text{i}}}{r_{\text{e}}} - {r_{\text{s}}}{r_{\text{e}}}\left( {t_{\text{i}}^{\text{2}} + r_{\text{i}}^{\text{2}}} \right)}}} \right) $ 131 Hz Schnupp
不对称$ {l_{{\text{sch}}}} = {l_x} - {l_y} $ 0.08 m DARM偏移 $ \Delta {L_{{\text{DC}}}} $ 10–13 m 高阶模耦合 $ {q_{{\text{HOM}}}} $ 1 × 10–7 W/RAN $ {k_{{\text{HOM}}}} $ 8 × 10–17 m/Hz 
DownLoad: CSV
表 2 熔融石英和硅材料的物理性质对比
Table 2. Comparison of physical properties of fused silica and silicon materials.
比较参数 硅(~123 K) 熔融石英(~300 K) 密度/(g·cm–3) 3.43 2.21 折射率(@1.5 μm) ~3.4841 1.445 热膨胀系数/K–1 0.001 × 10–6 5.5 × 10–7 热导率/
(W·(m K)–1)598.3 1.38 吸收系数/cm–1 1.11×10 @1064 nm 4×10–6@1064 nm 3.2×10–8 @1550 nm 2×10–5@1550 nm 机械损耗角/rad 0.00139 × 10–6 1 × 10–4 杨氏模量/GPa 131.1 73 泊松比 0.279 0.17
DownLoad: CSV
-
[1] Abbott B P, Abbott R, Abbott T D, et al. 2016 Phys. Rev. Lett. 116 061102
Google Scholar
[2] Abbott B P, Abbott R, Abbott T D, et al. 2016 Phys. Rev. Lett. 116 241103
Google Scholar
[3] Vermeulen S M, Relton P, Grote H, et al. 2021 Nature 600 424
Google Scholar
[4] Bailes M, Berger B K, Brady P R, et al. 2021 Nat. Rev. Phys. 3 344
Google Scholar
[5] Abbott R, Abbott T D, Abraham S, et al. 2021 Astrophys. J. Lett. 915 L5
Google Scholar
[6] Badaracco F, Rossi C D, Fiori I, Harms J, Miyo K, Paoletti F, Tanaka T, Washimi T, Yokozawa T 2021 Phys. Rev. D 104 042006
Google Scholar
[7] Hall E D, Kuns K, Smith J R, et al. 2021 Phys. Rev. D 103 122004
Google Scholar
[8] Buikema A, Cahillane C, Mansell G L, et al. 2020 Phys. Rev. D 102 062003
Google Scholar
[9] Adhikari R X 2014 Rev. Mod. Phys. 86 121
Google Scholar
[10] Bond C, Brown D, Freise A, Strain K A 2016 Living Rev. Relativ. 19 3
Google Scholar
[11] Matichard F, Lantz B, Mittleman R, et al. 2015 Classical Quant. Grav. 32 185003
Google Scholar
[12] P. Nguyen, Schofield R M S, Effler A, et al. 2021 Classical Quant. Grav. 38 145001
Google Scholar
[13] Adhikari R X, Arai K, Brooks A F, et al. 2020 Classical Quant. Grav. 37 165003
Google Scholar
[14] Hammond G, Hild S, Pitkin M 2014 J. Mod. Optic. 61 S10
Google Scholar
[15] Heurs M 2018 Philos. T. R. Soc. A 376 20170289
Google Scholar
[16] Danilishin S L, Khalili F Y, Miao H 2019 Living Rev. Relativ. 22 2
Google Scholar
[17] Sigg D 1997 LIGO Report No. LIGO- T970084-00 D
[18] Rana A 2004 Ph. D. Dissertation (Cambridge: Massachusetts Institute of Technology)
[19] Somiya K, Chen Y 2006 Phys. Rev. D 73 122005
Google Scholar
[20] Izumi K, Sigg D, Kawabe K 2016 LIGO Report No. LIGO-T1500325
[21] Izumi K, Sigg D, Kawabe K 2016 LIGO Report No. LIGO-T1500461
[22] Izumi K, Sigg D, Kawabe K 2016 LIGO Report No. LIGO-T1500559
[23] Cahillane C 2021 Ph. D. Dissertation (Pasadena: California Institute of Technology)
[24] Cahillane C, Mansell G L, Sigg D 2021 Opt. Express 29 42144
Google Scholar
[25] Buonanno A, Chen Y 2001 Phys. Rev. D 64 042006
Google Scholar
[26] Pitkin M, Reid S, Rowan S, Hough J 2011 Living Rev. Relativ. 14 5
Google Scholar
[27] Kwee P 2010 Ph. D. Dissertation (Hanover: Wilhelm Leibniz University)
[28] Chen Z, Guo M, Zhang R, Zhou B, Wei Q 2018 Sensors 18 02603
Google Scholar
[29] Degallaix J, Komma J, Forest D, Hofmann G 2014 Classical Quant. Grav. 31 185010
Google Scholar
[30] Khalaidovski A, Steinlechner J, Schnabel R 2013 Classical Quant. Grav. 30 165001
Google Scholar
[31] Biscans S, Gras S, Blair C D, Driggers J, Evans M, Fritschel P, Hardwick T, Mansell G 2019 Phys. Rev. D 100 122003
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4236
- PDF Downloads: 162
- Cited By: 0
