-
Quantum nonlocal correlation is one of the important features that distinguish the quantum theory from classical theory. As a typical quantum mixed state, the study of quantum nonlocal correlation based on the “X” state is of great importance for the verification of the correctness of quantum theory and the application of quantum information theory. In this work, with the traditional Clauser-Horne-Shimony-Holt (CHSH) inequality testing for quantum nonlocal correlations, we propose a strategy for testing the quantum nonlocal correlations based on the geometric interpretation of the “X” state. By using the geometric interpretation of the “X” state, which is described by the transform of Bloch sphere, it is possible to investigate the optimal selection of measurement settings. The maximum value of CHSH inequalities can also obtained from the physical images. Finally, the range of parameters for a successful quantum nonlocal correlation testing based on the CHSH inequality for the “X” state is studied. The results show that when
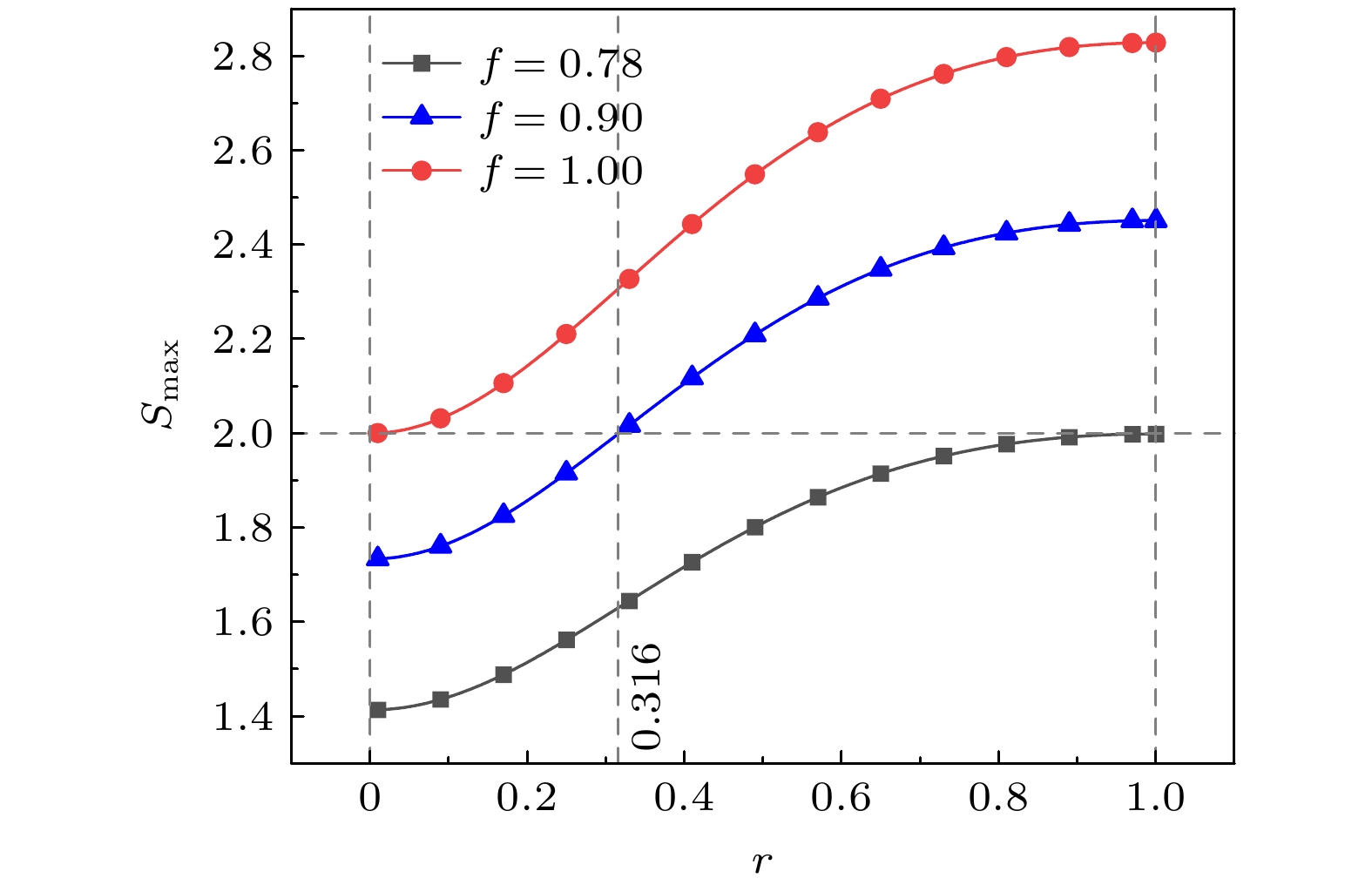
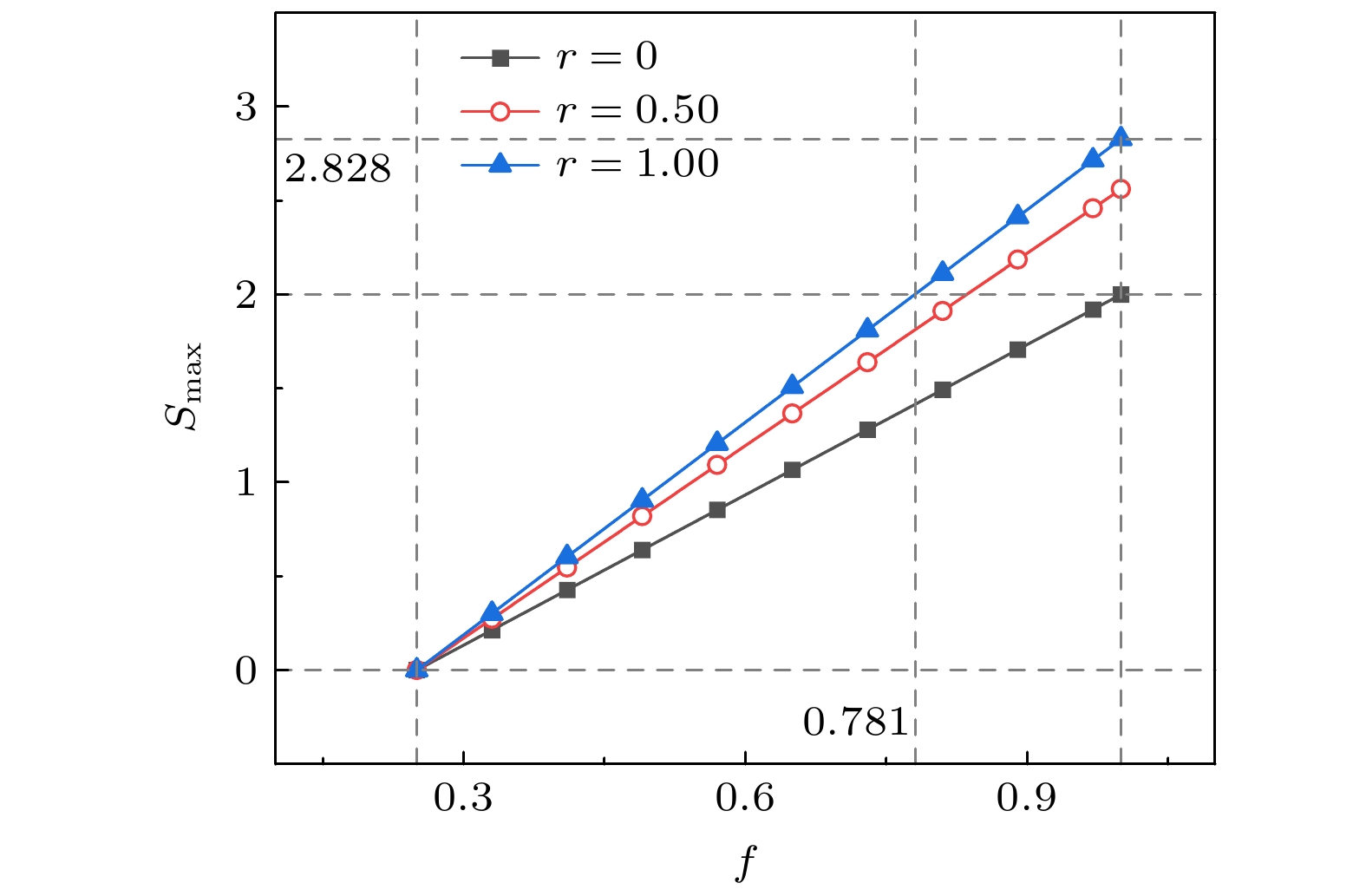
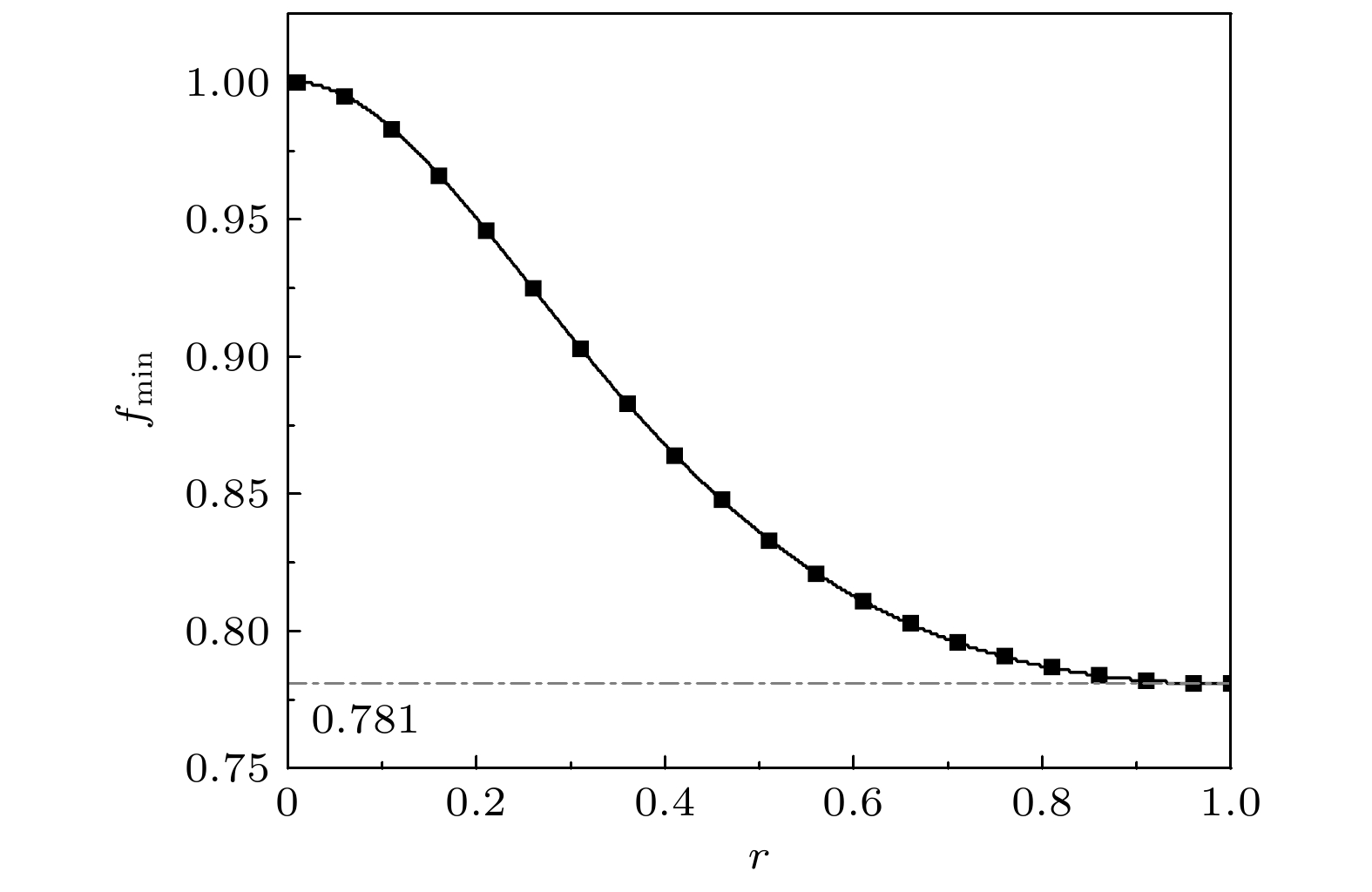
$f = 1$ , the “X” state will be reduced to a normal pure entangled state, and the quantum nonlocal correlation testing results are in full agreement with the traditional ones. This result proves the correctness of the geometric interpretation strategy proposed in this work. When$f \lt 1$ , only some of the “X” states can be used for e successfully testing the quantum nonlocal correlations. It is also found that the range of fidelity values that can successfully test the quantum nonlocal correlations will be further increased by increasing the values of r. In particular, when r = 1, the range of fidelity value will reach a largest one (e.g.$f \gt 0.781$ ). The results in this work can provide the reference for experimentally testing the quantum nonlocal correlation by using the “X” state.-
Keywords:
- quantum nonlocal correlation /
- X state /
- CHSH inequality /
- geometric interpretation
[1] Einstein A, Podolsky B, Rosen N 1935 Phys. Rev. 47 777
Google Scholar
[2] Chen Y A, Zhang Q, Chen T Y, et al. 2021 Nature 589 214
Google Scholar
[3] Zhang X, Li H O, Cao G, Xiao M, Guo G C, Guo G P 2019 Nat. Sci. Rev. 6 32
Google Scholar
[4] Horodecki R 2021 arXiv: 2103.07712 v2 [quant-ph]
[5] Bell J S 1964 Physics 1 195
Google Scholar
[6] Clauser J F, Horne M A, Shimony A, Holt R A 1969 Phys. Rev. Lett. 23 880
Google Scholar
[7] Freedman S J, Clauser J F 1972 Phys. Rev. Lett. 28 938
Google Scholar
[8] Aspect A, Dalibard J, Roger G 1982 Phys. Rev. Lett. 49 1804
Google Scholar
[9] Collins D, Gisin N, Linden N, Massar S, Popescu S 2002 Phys. Rev. Lett. 88 040404
Google Scholar
[10] Collins D, Gisin N 2004 J. Math. Phys. 37 1775
Google Scholar
[11] Mermin N D 1990 Phys. Rev. Lett. 65 1838
Google Scholar
[12] Ardehali M 1992 Phys. Rev. A 46 5375
Google Scholar
[13] Belinskiĭ A, Klyshko D N 1993 Phys. Usp. 36 653
Google Scholar
[14] Greenberger D M, Horne M A, Shimony A, Zeilinger A 1990 Am. J. Phys. 58 1131
Google Scholar
[15] Hardy L 1993 Phys. Rev. Lett. 71 1665
Google Scholar
[16] Kim J H, Chae J W, Jeong Y C, Kim Y H 2022 J. Korean Phys. Soc. 80 203
Google Scholar
[17] Singh J, Ghosh S, Arvind, Goyal S K 2021 Phys. Lett. A 392 127158
Google Scholar
[18] Koga J I, Kimura G, Maeda K 2018 Phys. Rev. A 97 062338
Google Scholar
[19] Seiler J, Strohm T, Schleich W P 2021 Phys. Rev. A 104 032218
Google Scholar
[20] Werner R F 1989 Phys. Rev. A 40 4277
Google Scholar
[21] Zhang Y S, Huang Y F, Li C F, Guo G C 2002 Phys. Rev. A 66 062315
Google Scholar
[22] Yu T, Eberly J 2007 Quantum Inf. Comput. 7 459
[23] Shi J D, Wu T, Song X K, Ye L 2014 Quantum Inf. Process. 13 1045
Google Scholar
[24] Namitha C, Satyanarayana S 2018 J. Phys. B:At. Mol. Opt. 51 045506
Google Scholar
[25] Mishra S, Thapliyal K, Pathak A, Venugopalan A 2022 Quantum Inf. Process. 21 1
Google Scholar
[26] Guo Y N, Peng H P, Zeng K, Wang G Y 2020 Quantum Inf. Process. 19 1
Google Scholar
[27] 刘晋, 缪波, 胡强, 樊代和 2020 量子光学学报 26 6
Google Scholar
Liu J, Miu B, Hu Q, Fan D H 2020 J. Quantum Opt. 26 6
Google Scholar
[28] 石名俊, 杜江峰, 朱栋培, 阮图南 2000 49 1912
Google Scholar
Shi M J, Du J F, Zhu D P, Ruan T N 2000 Acta Phys. Sin. 49 1912
Google Scholar
[29] Connes A, Zagier D 2007 Am. Math. Mon. 114 909
Google Scholar
-
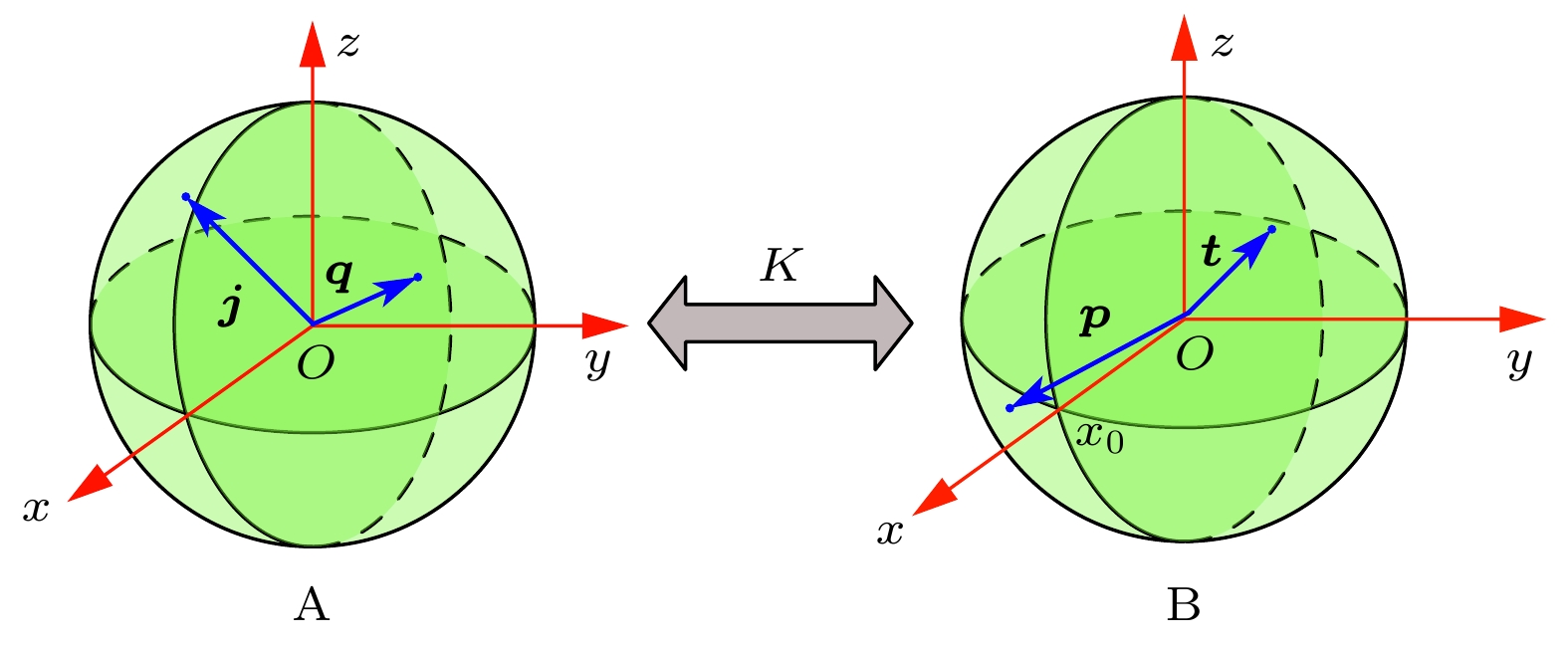
图 1 基于CHSH不等式的Bloch球表示图. 左右两个Bloch球分别代表A和B两个系统, 它们之间的关系由一个关联矩阵K进行描述.
${\boldsymbol{j}}$ 和${\boldsymbol{q}}$ 表示A系统中的两个测量方向,${\boldsymbol{p}}$ 和${\boldsymbol{t}}$ 表示B系统中的两个测量方向Figure 1. Diagram of Bloch ball representation based on CHSH inequality. The left and right Bloch sphere represents the two sub-system A and B, respectively. The relationship between them is described by a correlation matrix K.
${\boldsymbol{j}}$ and${\boldsymbol{q}}$ represents the two measurement directions in system A,${\boldsymbol{p}}$ and${\boldsymbol{t}}$ represents the two measurement directions in system B.
图 2 将关联矩阵K作用于B系统后的Bloch球表示图. 其中A系统的Bloch球保持不变, B系统的Bloch球受关联矩阵K的影响而发生改变. 两系统间的关联由单位矩阵I来描述
Figure 2. The Bloch sphere representation diagram by applying the correlation matrix K to system B. The Bloch sphere of system A keep constant. The Bloch sphere of system B is changed. The correlation between two systems is described by the unit matrix I.
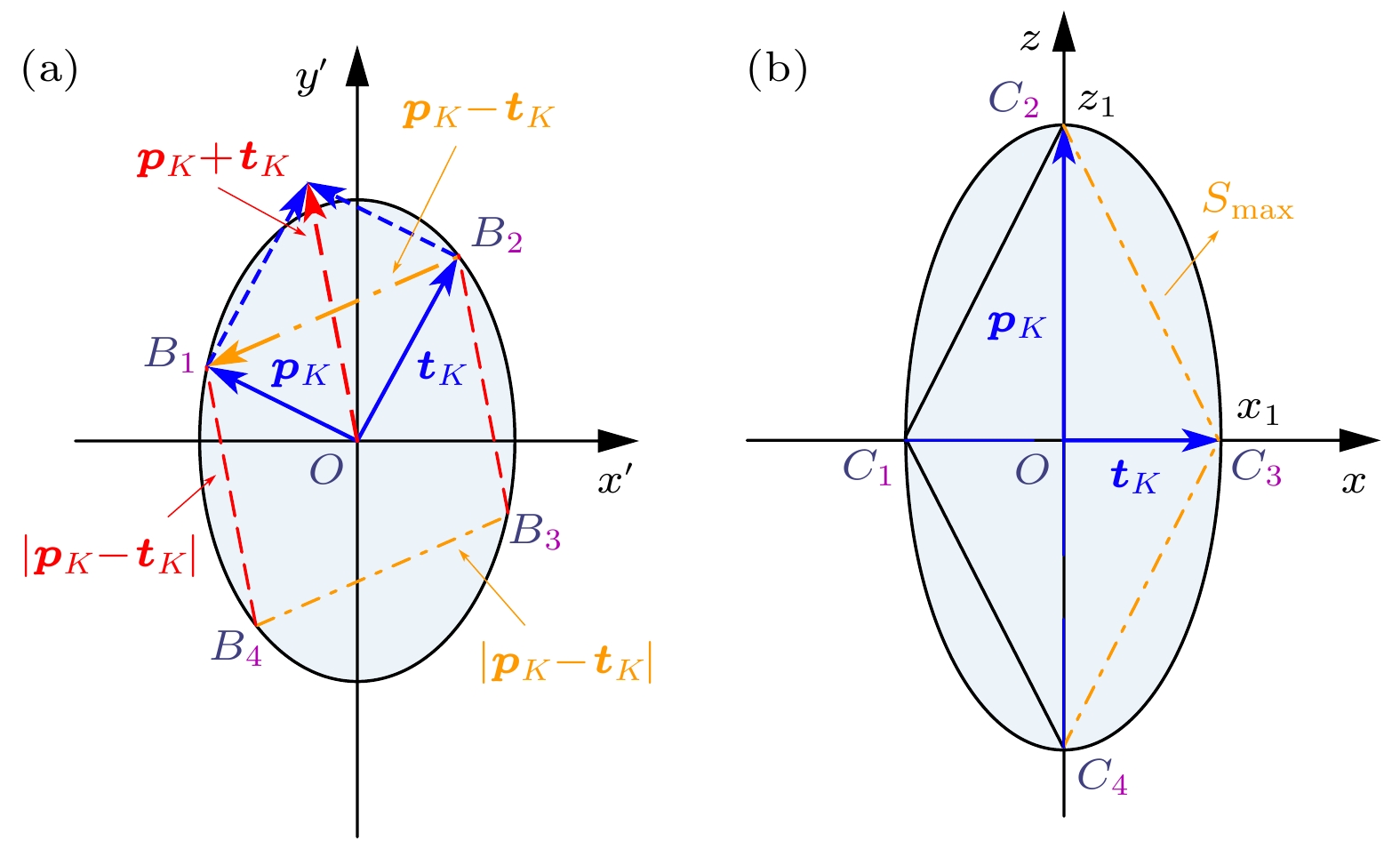
图 3 B系统Bloch球退变为一椭圆平面时的表示图 (a)向量
${{\boldsymbol{p}}_K}$ 在椭圆上的交点为${B_1}$ , 向量${{\boldsymbol{t}}_K}$ 在椭圆上的交点是${B_2}$ , 红色虚线表示向量${{\boldsymbol{p}}_K} + {{\boldsymbol{t}}_K}$ , 橙色点划线表示向量${{\boldsymbol{p}}_K} - {{\boldsymbol{t}}_K}$ ; (b) 向量${{\boldsymbol{p}}_K}$ 在椭圆上的交点是${C_2}$ , 向量${{\boldsymbol{t}}_K}$ 在椭圆上的交点是${C_3}$ , 橙色点划线表示最大期望值${S_{\max }}$ Figure 3. Diagram of elliptic plane when the Bloch sphere of system B is changed: (a) The intersection of vector
${{\boldsymbol{p}}_K}$ on the ellipse is${B_1}$ , the intersection of vector${{\boldsymbol{t}}_K}$ on the ellipse is${B_2}$ . The red dashed line indicates vector${{\boldsymbol{p}}_K} + {{\boldsymbol{t}}_K}$ , and the orange dotted line indicates vector${{\boldsymbol{p}}_K} - {{\boldsymbol{t}}_K}$ . (b) The intersection of vector${{\boldsymbol{p}}_K}$ on the ellipse is${C_2}$ , and the intersection of vector${{\boldsymbol{t}}_K}$ on the ellipse is${C_3}$ . The orange dotted line indicates the maximum expectation value of${S_{\max }}$ .
图 4 在不同保真度f下,
${S_{\max }}$ 随r的变化关系图Figure 4. Plot of
${S_{\max }}$ vs. r under different values of fidelity f.
图 5 在不同r下,
${S_{\max }}$ 随保真度f的变化关系图Figure 5. Plot of
${S_{\max }}$ vs. fidelity f under different values of r.
图 6
${f_{\min }}$ 随r的变化关系图Figure 6. Plot of
${f_{\min }}$ vs. r.
图 7
${S_{\max }}$ 随保真度f和r的变化关系图Figure 7. Plot of
${S_{\max }}$ vs. fidelity f and r. -
[1] Einstein A, Podolsky B, Rosen N 1935 Phys. Rev. 47 777
Google Scholar
[2] Chen Y A, Zhang Q, Chen T Y, et al. 2021 Nature 589 214
Google Scholar
[3] Zhang X, Li H O, Cao G, Xiao M, Guo G C, Guo G P 2019 Nat. Sci. Rev. 6 32
Google Scholar
[4] Horodecki R 2021 arXiv: 2103.07712 v2 [quant-ph]
[5] Bell J S 1964 Physics 1 195
Google Scholar
[6] Clauser J F, Horne M A, Shimony A, Holt R A 1969 Phys. Rev. Lett. 23 880
Google Scholar
[7] Freedman S J, Clauser J F 1972 Phys. Rev. Lett. 28 938
Google Scholar
[8] Aspect A, Dalibard J, Roger G 1982 Phys. Rev. Lett. 49 1804
Google Scholar
[9] Collins D, Gisin N, Linden N, Massar S, Popescu S 2002 Phys. Rev. Lett. 88 040404
Google Scholar
[10] Collins D, Gisin N 2004 J. Math. Phys. 37 1775
Google Scholar
[11] Mermin N D 1990 Phys. Rev. Lett. 65 1838
Google Scholar
[12] Ardehali M 1992 Phys. Rev. A 46 5375
Google Scholar
[13] Belinskiĭ A, Klyshko D N 1993 Phys. Usp. 36 653
Google Scholar
[14] Greenberger D M, Horne M A, Shimony A, Zeilinger A 1990 Am. J. Phys. 58 1131
Google Scholar
[15] Hardy L 1993 Phys. Rev. Lett. 71 1665
Google Scholar
[16] Kim J H, Chae J W, Jeong Y C, Kim Y H 2022 J. Korean Phys. Soc. 80 203
Google Scholar
[17] Singh J, Ghosh S, Arvind, Goyal S K 2021 Phys. Lett. A 392 127158
Google Scholar
[18] Koga J I, Kimura G, Maeda K 2018 Phys. Rev. A 97 062338
Google Scholar
[19] Seiler J, Strohm T, Schleich W P 2021 Phys. Rev. A 104 032218
Google Scholar
[20] Werner R F 1989 Phys. Rev. A 40 4277
Google Scholar
[21] Zhang Y S, Huang Y F, Li C F, Guo G C 2002 Phys. Rev. A 66 062315
Google Scholar
[22] Yu T, Eberly J 2007 Quantum Inf. Comput. 7 459
[23] Shi J D, Wu T, Song X K, Ye L 2014 Quantum Inf. Process. 13 1045
Google Scholar
[24] Namitha C, Satyanarayana S 2018 J. Phys. B:At. Mol. Opt. 51 045506
Google Scholar
[25] Mishra S, Thapliyal K, Pathak A, Venugopalan A 2022 Quantum Inf. Process. 21 1
Google Scholar
[26] Guo Y N, Peng H P, Zeng K, Wang G Y 2020 Quantum Inf. Process. 19 1
Google Scholar
[27] 刘晋, 缪波, 胡强, 樊代和 2020 量子光学学报 26 6
Google Scholar
Liu J, Miu B, Hu Q, Fan D H 2020 J. Quantum Opt. 26 6
Google Scholar
[28] 石名俊, 杜江峰, 朱栋培, 阮图南 2000 49 1912
Google Scholar
Shi M J, Du J F, Zhu D P, Ruan T N 2000 Acta Phys. Sin. 49 1912
Google Scholar
[29] Connes A, Zagier D 2007 Am. Math. Mon. 114 909
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4385
- PDF Downloads: 60
- Cited By: 0
