-
Ligand decoration of noble metallic nanoparticles is often needed for some applications, such as biochemical sensing, catalysis and nanotechnology, and the understanding of its process is of great importance. The second harmonic scattering (SHS) technique with advantages of surface-sensitivity and label-free detection, provides intrinsic information for such a research. In this work, the second harmonic(SH) scattering patterns of two types of ligands (cetyltrimethylammonium chloride and L-cysteine) capped gold nanoparticles (GNPs) with the same radii are measured. Both the intensities and shapes of the SH scattering patterns are changed after the ligand exchange process. In order to explain the pattern changes, the analytic expressions of SH scattering are derived theoretically for a relatively large nanoparticle based on Dadap’s multipolar theory. Considering the derived relationship between the multipole (up to octopole) contributions and the power of the nanosphere radius, the effective size effect is introduced to express the SH scattering signal change for different ligand decorations and well explain the experimental results. This theory provides a new perspective of the SH scattering response to different capping ligands and offers a possible quantitative method to analyze interface physical chemistry for ligands on the surface of nanoparticles.
-
Keywords:
- second harmonic scattering /
- gold nanoparticle /
- ligand decoration /
- multipolar decomposition
[1] Zhou J, Ralston J, Sedev R, Beattie D A 2009 J. Colloid Interface Sci. 331 251
Google Scholar
[2] Bachelier G, Russier-Antoine I, Benichou E, Jonin C, Brevet P F 2008 J. Opt. Soc. Am. B: Opt. Phys. 25 955
Google Scholar
[3] Dinkel R, Peukert W, Braunschweig B 2017 J. Phys. Condens. Matter 29 133002
Google Scholar
[4] Dinkel R, Jakobi J, Ziefuss A R, Barcikowski S, Braunschweig B, Peukert W 2018 J. Phys. Chem. C 122 27383
Google Scholar
[5] Butet J, Brevet P F, Martin O J F 2015 Acs Nano 9 10545
Google Scholar
[6] 邹伟博, 周骏, 金理, 张昊鹏 2012 61 097805
Google Scholar
Zou W B, Zhou J, Jin L, Zhang H P 2012 Acta Phys. Sin. 61 097805
Google Scholar
[7] 王凯, 杨光, 龙华, 李玉华, 戴能利, 陆培祥 2008 57 3862
Google Scholar
Wang K, Yang G, Long H, Li Y H, Dai N L, Lu P X 2008 Acta Phys. Sin. 57 3862
Google Scholar
[8] Kuchler M, Rebentrost F 1993 Phys. Rev. Lett. 71 2662
Google Scholar
[9] Rebentrost F 1995 Prog. Surf. Sci. 48 71
Google Scholar
[10] Nikoobakht B, El-Sayed M A 2001 Langmuir 17 6368
Google Scholar
[11] Sawaguchi T, Sato Y, Mizutani F 2001 Phys. Chem. Chem. Phys. 3 3399
Google Scholar
[12] Zhang P, Sham T K 2002 Appl. Phys. Lett. 81 736
Google Scholar
[13] Gan W, Xu B, Dai H L 2011 Angew. Chem. Int. Ed. 50 6622
Google Scholar
[14] El Harfouch Y, Benichou E, Bertorelle F, Russier-Antoine I, Jonin C, Lascoux N, Brevet P F 2012 J. Phys. Condens. Matter 24 124104
Google Scholar
[15] Ngo H M, Ledoux-Rak I 2014 Proc. SPIE 9171 91710Y
[16] Park J W, Shumaker-Parry J S 2015 ACS Nano 9 1665
Google Scholar
[17] Van Steerteghem N, Van Cleuvenbergen S, Deckers S, Kumara C, Dass A, Hakkinen H, Clays K, Verbiest T, Knoppe S 2016 Nanoscale 8 12123
Google Scholar
[18] Sipe J E, So V C Y, Fukui M, Stegeman G I 1980 Phys. Rev. B 21 4389
Google Scholar
[19] Dadap J I, Shan J, Eisenthal K B, Heinz T F 1999 Phys. Rev. Lett. 83 4045
Google Scholar
[20] Russier-Antoine I, Huang J, Benichou E, Bachelier G, Jonin C, Brevet P F 2008 Chem. Phys. Lett. 450 345
Google Scholar
[21] Haber L H, Kwok S J J, Semeraro M, Eisenthal K B 2011 Chem. Phys. Lett. 507 11
Google Scholar
[22] Karam T E, Haber L H 2014 J. Phys. Chem. C 118 642
Google Scholar
[23] Das A, Chakrabarti A, Das P K 2017 Nanoarmoring of Enzymes: Rational Design of Polymer-Wrapped Enzymes pp33–58
[24] Troiano J M, Kuech T R, Vartanian A M, Torelli M D, Sen A, Jacob L M, Hamers R J, Murphy C J, Pedersen J A, Geiger F M 2016 J. Phys. Chem. C 120 20659
Google Scholar
[25] Buck M, Eisert F, Fischer J, Grunze M, Trager F 1991 Appl. Phys. A 53 552
Google Scholar
[26] Dinkel R, Braunschweig B, Peukert W 2016 Phys. Chem. C 120 1673
Google Scholar
[27] Butet J, Maurice A, Bergmann E, Bachelier G, Russier-Antoine I, Ray C, Bonhomme O, Jonin C, Benichou E, Brevet P F 2019 Metal Nanostruct. Photonics 105
[28] Ray P C 2010 Chem. Rev. 110 5332
Google Scholar
[29] Das K, Uppal A, Saini R K, Varshney G K, Mondal P, Gupta P K 2014 Spectrochim. Acta, Part A 128 398
Google Scholar
[30] Galletto P, Brevet P F, Girault H H, Antoine R, Broyer M 1999 J. Phys. Chem. B 103 8706
[31] Nappa J, Revillod G, Russier-Antoine I, Benichou E, Jonin C, Brevet P F 2005 Phys. Rev. B 71 165407
Google Scholar
[32] Nappa J, Russier-Antoine I, Benichou E, Jonin C, Brevet P F 2006 J. Chem. Phys. 125 184712
Google Scholar
[33] Butet J, Bachelier G, Russier-Antoine I, Jonin C, Benichou E, Brevet P F 2010 Phys. Rev Lett. 105 077401
Google Scholar
[34] Svoboda K, Block S M 1994 Opt. Lett. 19 930
Google Scholar
[35] Zheng Y, Zhong X, Li Z, Xia Y J P 2014 Part. Part. Syst. Char. 31 266
Google Scholar
[36] Kutz R B, Braunschweig B, Mukherjee P, Behrens R L, Dlott D D, Wieckowski A 2011 J. Catal. 278 181
Google Scholar
[37] Dadap J I, Shan J, Heinz T F 2004 J. Opt. Soc. Am. B 21 1328
Google Scholar
-
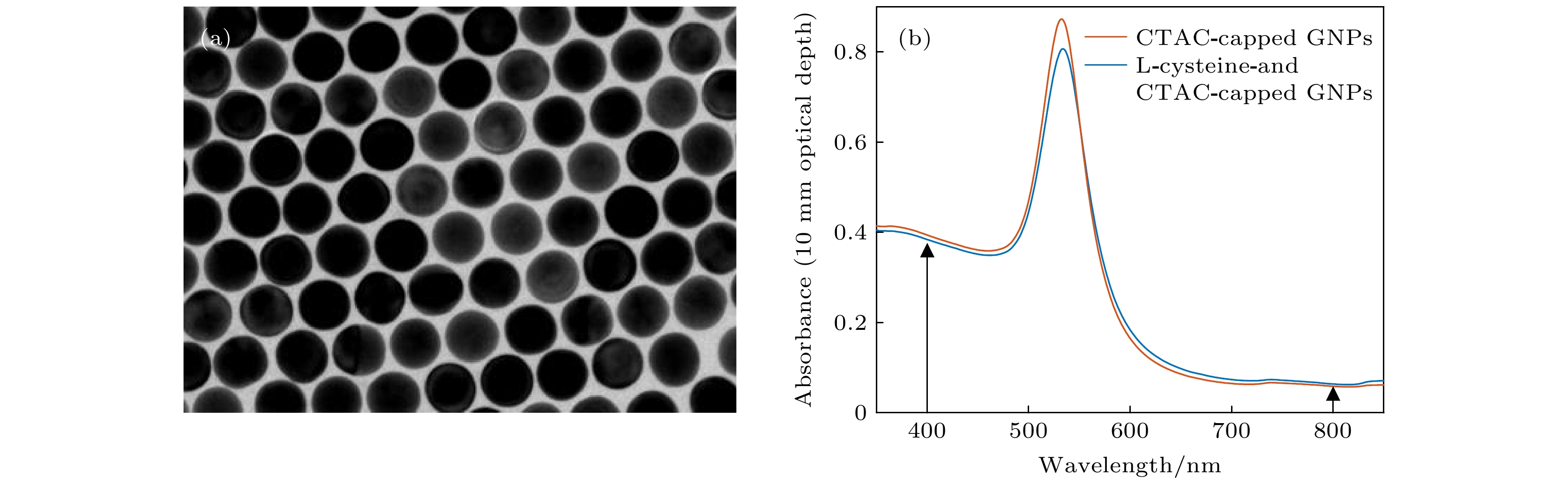
图 1 (a) 60 nm直径大小的CTAC修饰的金纳米颗粒的TEM图像; (b) 两组混合液的UV-Vis吸收光谱, 左右箭头分别代表SH散射光波长和激发光波长
Figure 1. (a) TEM image of 60 nm CTAC-capped gold nanoparticles (GNPs); (b) UV-Vis absorbance spectra of the CTAC-capped GNP and L-cysteine/CTAC-capped GNP colloidal solutions. The left and right arrows indicate the SH wavelength and the excitation light wavelength, respectively.
图 2 (a) 激发光光谱; (b) 垂直偏振入射下的CTAC修饰的金纳米颗粒的p-偏振SH散射光光谱
Figure 2. (a) The spectrum of excitation light; (b) the p-polarized spectrum of SH scattering light from the CTAC-capped GNP under vertically-polarized incidence.
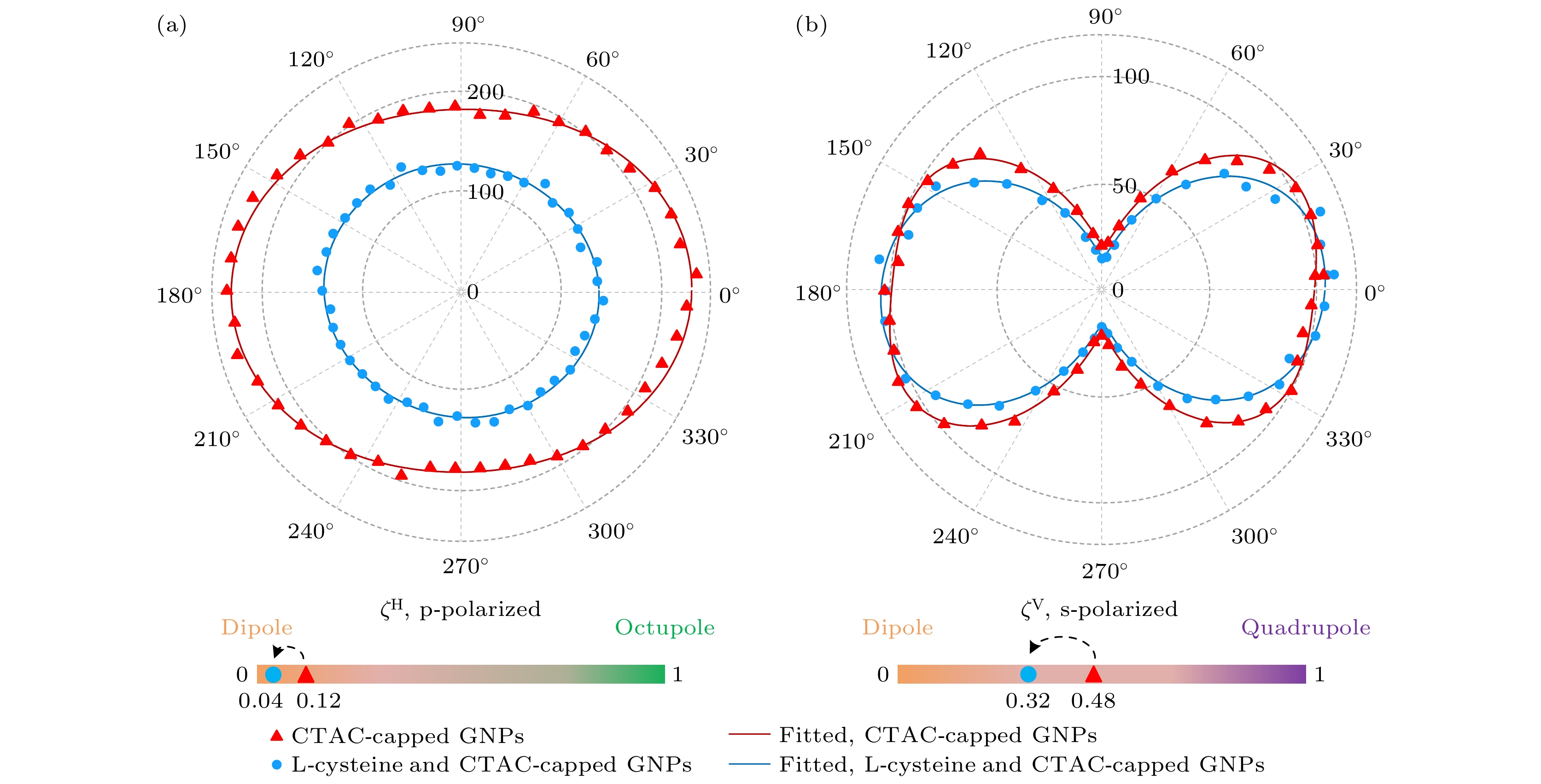
图 3 60 nm金颗粒在不同修饰配体下的随入射光偏振角度变化的(a) p偏振和(b) s偏振的SH散射图样, 其中实心圆和三角为实验点, 实线为拟合实验点. 两个权重因子
${\zeta ^{\rm{V}}}$ 和${\zeta ^{\rm{H}}}$ 在配体交换过程前后的变化也在图中展示出来Figure 3. (a) The p-polarized and (b) s-polarized SH scattering patterns of 60-nm GNPs with different surface ligand coverage as a function of the incoming fundamental beam polarization angle: experimental points (filled circles and triangles) and fit to the experimental points (solid line). The changes of
${\zeta ^{\rm{V}}}$ and${\zeta ^{\rm{H}}}$ for the ligand-exchange process are also shown.
图 4 球体的SH散射模型原理图
Figure 4. Schematic of SH scattering model for a sphere.
表 1 沿x轴方向偏振的激发场下的
$ b_{ijk}^{lm} $ 表达式Table 1. Coefficients
$ b_{ijk}^{lm} $ for an excitation field polarized along x direction.$ (l, m) $ $ b_{ \bot \bot \bot }^{lm}/E_0^2 $ $ b_{ \bot \parallel \parallel }^{lm}/E_0^2 $ $b_{\parallel \bot \parallel , {{E} } }^{lm}/E_0^2$ $b_{\parallel \bot \parallel , {{M} } }^{lm}/E_0^2$ $ (1, 0) $ $\dfrac{4}{5}\sqrt {\dfrac{\text{π} }{3} } {\rm{i}}L_ \bot ^{ {{\rm{E}}} 1}(\omega )L_ \bot ^{ {{\rm{E}}} 2}(\omega ){K_1}a$ $\begin{gathered} \dfrac{2}{5}\sqrt {\dfrac{\text{π} }{3} } {\rm{i} }L_\parallel ^{ { {\rm{E} } } 1}(\omega ) \\ \times[5 L_\parallel ^{ { {\rm{M} } } 1}(\omega ) + 3 L_\parallel ^{ { {\rm{E} } } 2}(\omega )]{K_1}a \end{gathered}$ $\begin{gathered} \dfrac{1}{5}\sqrt {\dfrac{ {2\text{π} } }{3} } [ - 5 L_ \bot ^{ { {\rm{E} } } 1}(\omega )L_\parallel ^{ { {\rm{M} } } 1}(\omega ) \\ + 3 L_ \bot ^{ { {\rm{E} } } 1}(\omega )L_\parallel ^{ { {\rm{E} } } 2}(\omega ) \\ -2 L_ \bot ^{ { {\rm{E} } } 2}(\omega )L_\parallel ^{ { {\rm{E} } } 1}(\omega )]{K_1}a \\ \end{gathered}$ 0 $ (2, 0) $ $- \dfrac{2}{3}\sqrt {\dfrac{\text{π} }{5} } {[L_ \bot ^{ {{\rm{E}}} 1}(\omega )]^2}$ $\dfrac{2}{3}\sqrt {\dfrac{\text{π} }{5} } {[L_\parallel ^{ { {\rm{E} } } 1}(\omega )]^2}$ $2\sqrt {\dfrac{ {2\text{π} } }{ {15} } } {\rm{i}}[L_ \bot ^{ {E} 1}(\omega )L_\parallel ^{ {{\rm{E}}} 1}(\omega )]$ 0 $ (2, \pm 2) $ $\sqrt {\dfrac{ {2\text{π} } }{ {15} } } {[L_ \bot ^{ {{\rm{E}}} 1}(\omega )]^2}$ $- \sqrt {\dfrac{ {2\text{π} } }{ {15} } } {[L_\parallel ^{ {{\rm{E}}} 1}(\omega )]^2}$ $- 2\sqrt {\dfrac{\text{π} }{5} } {\rm{i}}[L_ \bot ^{ {{\rm{E}}} 1}(\omega )L_\parallel ^{ {{\rm{E}}} 1}(\omega )]$ 0 $ (3, 0) $ $\dfrac{4}{ {35} }\sqrt {7\text{π} } {\rm{i}}L_ \bot ^{ {{\rm{E}}} 1}(\omega )L_ \bot ^{ {{\rm{E}}} 2}(\omega ){K_1}a$ $\dfrac{4}{ {35} }\sqrt {7\text{π} } {\rm{i}}L_\parallel ^{ {{\rm{E}}} 1}(\omega )L_\parallel ^{ {{\rm{E}}} 2}(\omega ){K_1}a$ $\begin{gathered} - \dfrac{ {8\sqrt {21\text{π} } } }{ {105} }\left( {L_\parallel ^{ { {\rm{E} } } 1}(\omega )L_ \bot ^{ { {\rm{E} } } 2}(\omega )} \right. \\ \left. { + L_ \bot ^{ { {\rm{E} } } 1}(\omega )L_\parallel ^{ { {\rm{E} } } 2}(\omega )} \right){K_1}a \\ \end{gathered}$ 0 $ (3, \pm 2) $ $2\sqrt {\dfrac{ {2\text{π} } }{ {105} } } {\rm{i}}L_ \bot ^{ {{\rm{E}}} 1}(\omega )L_ \bot ^{ {{\rm{E}}} 2}(\omega ){K_1}a$ $- 2\sqrt {\dfrac{ {2\text{π} } }{ {105} } } {\rm{i}}L_\parallel ^{ {{\rm{E}}} 1}(\omega )L_\parallel ^{ {{\rm{E}}} 2}(\omega ){K_1}a$ $\begin{gathered} \dfrac{4}{3}\sqrt {\dfrac{ {2\text{π} } }{ {35} } } \left( {L_\parallel ^{ { {\rm{E} } } 1}(\omega )L_ \bot ^{ { {\rm{E} } } 2}(\omega )} \right. \\ \left. { + L_ \bot ^{ { {\rm{E} } } 1}(\omega )L_\parallel ^{ { {\rm{E} } } 2}(\omega )} \right){K_1}a \\ \end{gathered}$ 0 
DownLoad: CSV
表 2 不同的激发-辐射模式以及SH多极子与
$ {K_1}a $ 因子的幂次关系Table 2. The Excitation-radiation channels and the power relationship to the factor
$ ({K_1}a) $ with the electric field.基场多极子 SH场多极子 与$ ({K_1}a) $的幂
次关系SH场偏
振方向${{\rm{E}}} 1$ ${{\rm{E}}} 1$ ${{\rm{E}}} 1$ $ \propto {({K_1}a)^2} $ s/p ${{\rm{E}}} 1$ ${\rm{E}}2$ ${{\rm{E}}} 1$ $ \propto {({K_1}a)^3} $ p ${{\rm{E}}} 1$ ${\rm{M}}1$ ${{\rm{E}}} 1$ $ \propto {({K_1}a)^3} $ p ${{\rm{E}}} 1$ ${{\rm{E}}} 1$ ${\rm{E}}2$ $ \propto {({K_1}a)^3} $ s ${{\rm{E}}} 1$ ${\rm{E}}2$ ${{\rm{E}}} 3$ $ \propto {({K_1}a)^5} $ p
DownLoad: CSV
-
[1] Zhou J, Ralston J, Sedev R, Beattie D A 2009 J. Colloid Interface Sci. 331 251
Google Scholar
[2] Bachelier G, Russier-Antoine I, Benichou E, Jonin C, Brevet P F 2008 J. Opt. Soc. Am. B: Opt. Phys. 25 955
Google Scholar
[3] Dinkel R, Peukert W, Braunschweig B 2017 J. Phys. Condens. Matter 29 133002
Google Scholar
[4] Dinkel R, Jakobi J, Ziefuss A R, Barcikowski S, Braunschweig B, Peukert W 2018 J. Phys. Chem. C 122 27383
Google Scholar
[5] Butet J, Brevet P F, Martin O J F 2015 Acs Nano 9 10545
Google Scholar
[6] 邹伟博, 周骏, 金理, 张昊鹏 2012 61 097805
Google Scholar
Zou W B, Zhou J, Jin L, Zhang H P 2012 Acta Phys. Sin. 61 097805
Google Scholar
[7] 王凯, 杨光, 龙华, 李玉华, 戴能利, 陆培祥 2008 57 3862
Google Scholar
Wang K, Yang G, Long H, Li Y H, Dai N L, Lu P X 2008 Acta Phys. Sin. 57 3862
Google Scholar
[8] Kuchler M, Rebentrost F 1993 Phys. Rev. Lett. 71 2662
Google Scholar
[9] Rebentrost F 1995 Prog. Surf. Sci. 48 71
Google Scholar
[10] Nikoobakht B, El-Sayed M A 2001 Langmuir 17 6368
Google Scholar
[11] Sawaguchi T, Sato Y, Mizutani F 2001 Phys. Chem. Chem. Phys. 3 3399
Google Scholar
[12] Zhang P, Sham T K 2002 Appl. Phys. Lett. 81 736
Google Scholar
[13] Gan W, Xu B, Dai H L 2011 Angew. Chem. Int. Ed. 50 6622
Google Scholar
[14] El Harfouch Y, Benichou E, Bertorelle F, Russier-Antoine I, Jonin C, Lascoux N, Brevet P F 2012 J. Phys. Condens. Matter 24 124104
Google Scholar
[15] Ngo H M, Ledoux-Rak I 2014 Proc. SPIE 9171 91710Y
[16] Park J W, Shumaker-Parry J S 2015 ACS Nano 9 1665
Google Scholar
[17] Van Steerteghem N, Van Cleuvenbergen S, Deckers S, Kumara C, Dass A, Hakkinen H, Clays K, Verbiest T, Knoppe S 2016 Nanoscale 8 12123
Google Scholar
[18] Sipe J E, So V C Y, Fukui M, Stegeman G I 1980 Phys. Rev. B 21 4389
Google Scholar
[19] Dadap J I, Shan J, Eisenthal K B, Heinz T F 1999 Phys. Rev. Lett. 83 4045
Google Scholar
[20] Russier-Antoine I, Huang J, Benichou E, Bachelier G, Jonin C, Brevet P F 2008 Chem. Phys. Lett. 450 345
Google Scholar
[21] Haber L H, Kwok S J J, Semeraro M, Eisenthal K B 2011 Chem. Phys. Lett. 507 11
Google Scholar
[22] Karam T E, Haber L H 2014 J. Phys. Chem. C 118 642
Google Scholar
[23] Das A, Chakrabarti A, Das P K 2017 Nanoarmoring of Enzymes: Rational Design of Polymer-Wrapped Enzymes pp33–58
[24] Troiano J M, Kuech T R, Vartanian A M, Torelli M D, Sen A, Jacob L M, Hamers R J, Murphy C J, Pedersen J A, Geiger F M 2016 J. Phys. Chem. C 120 20659
Google Scholar
[25] Buck M, Eisert F, Fischer J, Grunze M, Trager F 1991 Appl. Phys. A 53 552
Google Scholar
[26] Dinkel R, Braunschweig B, Peukert W 2016 Phys. Chem. C 120 1673
Google Scholar
[27] Butet J, Maurice A, Bergmann E, Bachelier G, Russier-Antoine I, Ray C, Bonhomme O, Jonin C, Benichou E, Brevet P F 2019 Metal Nanostruct. Photonics 105
[28] Ray P C 2010 Chem. Rev. 110 5332
Google Scholar
[29] Das K, Uppal A, Saini R K, Varshney G K, Mondal P, Gupta P K 2014 Spectrochim. Acta, Part A 128 398
Google Scholar
[30] Galletto P, Brevet P F, Girault H H, Antoine R, Broyer M 1999 J. Phys. Chem. B 103 8706
[31] Nappa J, Revillod G, Russier-Antoine I, Benichou E, Jonin C, Brevet P F 2005 Phys. Rev. B 71 165407
Google Scholar
[32] Nappa J, Russier-Antoine I, Benichou E, Jonin C, Brevet P F 2006 J. Chem. Phys. 125 184712
Google Scholar
[33] Butet J, Bachelier G, Russier-Antoine I, Jonin C, Benichou E, Brevet P F 2010 Phys. Rev Lett. 105 077401
Google Scholar
[34] Svoboda K, Block S M 1994 Opt. Lett. 19 930
Google Scholar
[35] Zheng Y, Zhong X, Li Z, Xia Y J P 2014 Part. Part. Syst. Char. 31 266
Google Scholar
[36] Kutz R B, Braunschweig B, Mukherjee P, Behrens R L, Dlott D D, Wieckowski A 2011 J. Catal. 278 181
Google Scholar
[37] Dadap J I, Shan J, Heinz T F 2004 J. Opt. Soc. Am. B 21 1328
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4293
- PDF Downloads: 82
- Cited By: 0
