-
以量子信息领域中常使用的Werner态为研究对象, 详细地研究了其在两种非马尔科夫相位阻尼环境, 即Random-Telegraph (RT)噪声环境、Ornstein-Uhlenbeck (OU)噪声环境, 以及非马尔科夫振幅阻尼(AD)环境中演化后的量子非局域关联检验情况. 分别推导了Werner态在RT, OU以及AD环境中密度矩阵随时间的演化结果. 基于Clauser-Horne-Shimony-Holt (CHSH)不等式, 对演化后的量子态进行了详细的量子非局域关联检验研究. 结果表明, Werner态在RT噪声环境和AD环境中存在信息回流现象, 导致其量子非局域关联特性存在周期性振荡变化的现象, 即随演化时间的增加, 量子态能够从不具备量子非局域关联特性重新回到具有量子非局域关联特性的情况. 而在OU噪声环境中, 由于不存在信息回流现象, 量子非局域关联检验值将随演化时间的增加而降低. 同时, 本文还详细给出了Werner的保真度、量子态与非马尔科夫环境的耦合强度、OU噪声环境和AD环境的线宽、RT环境噪声的翻转率等参数与成功进行量子非局域关联检验的演化时间之间的关系.Research on whether quantum states retain quantum non-local correlation properties after evolving in non-Markovian environments has significant applications in the field of quantum information. In this work, we investigate the density matrix of quantum states evolving with time in various non-Markovian environments. Specifically, we examine two types of non-Markovian phase damping environments, namely random telegraph (RT) noise environment and Ornstein-Uhlenbeck (OU) noise environment, and non-Markovian amplitude damping (AD) environment. By utilizing the Clauser-Horne-Shimony-Holt (CHSH) inequality, a quantum non-local correlation testing of the Werner state after its evolution in these non-Markovian environments is conducted. The results show significant differences in the quantum non-local correlation testing results of the Werner state after evolving in different non-Markovian environments. Notably, the Werner state displays information backflow in the RT noise environment and the AD environment, resulting in periodic oscillations in its quantum non-local correlation testing. This suggests that under certain conditions, the quantum state can transition from a state without quantum non-local correlation back to a state with such a correlation as evolution time progresses. The results also show that the Werner state exhibits the information about backflow phenomena in RT noise environment and AD environment, leading to periodic oscillations in its quantum non-local correlation testing. Furthermore, these periods are inversely proportional to certain parameters, such as
$\sqrt {{{\left( {{{2\gamma } \mathord{\left/ {\vphantom {{2\gamma } a}} \right. } a}} \right)}^2} - 1} $ and$ \sqrt {2{\varGamma \mathord{\left/ {\vphantom {\varGamma \gamma }} \right. } \gamma } - {{\left( {{\varGamma \mathord{\left/ {\vphantom {\varGamma \gamma }} \right. } \gamma }} \right)}^2}} $ . On the contrary, in the OU noise environment, no information about backflow is obtained, thereby leading the value of the quantum non-local correlation test to increase with evolution time increasing. In most of AD and OU noise environments, there exists a specific maximum evolution time$\gamma {t_{\max }}$ in which successful quantum non-local correlation testing can be conducted. This maximum evolution time$\gamma {t_{\max }}$ shows a nonlinear variation with fidelity increasing and an inverse variation with$\varGamma /\gamma $ parameter increasing. In comparison, the maximum evolution time for successful quantum non-local correlation testing in the OU noise environment exceeds that in the AD environment under the same conditions, indicating that the AD environment exerts a more pronounced weakening effect on the quantum non-local correlation properties of the Werner state.
-
Keywords:
- quantum non-local correlation /
- Werner state /
- non-Markovian environment /
- Clauser-Horne-Shimony-Holt inequality /
- phase damping /
- amplitude damping
[1] Einstein A, Podolsky B, Rosen N 1935 Phys. Rev. Lett. 47 777
Google Scholar
[2] Gisin N, Ribordy G, Tittel W, Zbinden H 2002 Rev. Mod. Phys. 74 145
Google Scholar
[3] Bennett C H, Wiesner S J 1992 Phys. Rev. Lett. 69 2881
Google Scholar
[4] Bennett C H, Brassard G, Crépeau C, Jozsa R, Peres A, Wootters W K 1993 Phys. Rev. Lett. 70 1895
Google Scholar
[5] Bell J S 1964 Physics 1 195
Google Scholar
[6] Clauser J F, Horne M A, Shimony A, Holt R A 1969 Phys. Rev. Lett. 23 880
Google Scholar
[7] Horodecki R, Horodecki P, Horodecki M, Horodecki K 2009 Rev. Mod. Phys. 81 865
Google Scholar
[8] Collins D, Gisin N 2004 J. Phys. A: Math. Gen. 37 1775
Google Scholar
[9] Greenberger D M, Horne M A, Shimony A, Zeilinger A 1990 Am. J. Phys. 58 1131
Google Scholar
[10] Hardy L 1993 Phys. Rev. Lett. 71 1665
Google Scholar
[11] 胡强, 曾柏云, 辜鹏宇, 贾欣燕, 樊代和 2022 71 070301
Google Scholar
Hu Q, Zeng B Y, Gu P Y, Jia X Y, Fan D H 2022 Acta Phys. Sin. 71 070301
Google Scholar
[12] 曾柏云, 辜鹏宇, 蒋世民, 贾欣燕, 樊代和 2023 72 050301
Google Scholar
Zeng B Y, Gu P Y, Jiang S M, Jia X Y, Fan D H 2023 Acta Phys. Sin. 72 050301
Google Scholar
[13] Rivas Á, Huelga S F, Plenio M B 2014 Rep. Prog. Phys. 77 094001
Google Scholar
[14] Breuer H P, Laine E M, Piilo J, Vacchini B 2016 Rev. Mod. Phys. 88 021002
Google Scholar
[15] de Vicente J I, Spee C, Sauerwein D, Kraus B 2017 Phys. Rev. A 95 012323
Google Scholar
[16] Li L, Hall M J W, Wiseman H M 2018 Phys. Rep. 759 1
Google Scholar
[17] Weissman M B 1988 Rev. Mod. Phys. 60 537
Google Scholar
[18] Mi X, Cady J V, Zajac D M, Deelman P W, Petta J R 2017 Science 355 156
Google Scholar
[19] Groeblacher S, Trubarov A, Prigge N, Cole G D, Aspelmeyer M, Eisert J 2015 Nat. Commun. 6 7606
Google Scholar
[20] Potočnik A, Bargerbos A, Schröder F A Y N, Khan S A, Collodo M C, Gasparinetti S, Salathé Y, Creatore C, Eichler C, Türeci H E, Chin A W, Wallraff A 2018 Nat. Commun. 9 904
Google Scholar
[21] Haikka P, McEndoo S, De Chiara G, Palma G M, Maniscalco S 2011 Phys. Rev. A 84 031602
Google Scholar
[22] Utagi S, Srikanth R, Banerjee S 2020 Sci. Rep. 10 15049
Google Scholar
[23] Naikoo J, Banerjee S, Chandrashekar C M 2020 Phys. Rev. A 102 062209
Google Scholar
[24] Yu T, Eberly J 2007 Quantum Inf. Comput. 7 459
Google Scholar
[25] Kraus K 1971 Ann. Phys. 64 311
Google Scholar
[26] Rivas Á, Huelga S F, Plenio M B 2010 Phys. Rev. Lett. 105 050403
Google Scholar
[27] Breuer H P, Laine E M, Piilo J 2009 Phys. Rev. Lett. 103 210401
Google Scholar
[28] Pinto J P, Karpat G, Fanchini F F 2013 Phys. Rev. A. 88 034304
Google Scholar
[29] Yu T, Eberly J 2010 Opt. Commun. 283 676
Google Scholar
[30] Bellomo B, Franco R L, Compagno G 2007 Phys. Rev. Lett. 99 160502
Google Scholar
[31] Horodecki R, Horodecki P, Horodecki M 1995 Phys. Lett. A 200 340
Google Scholar
-
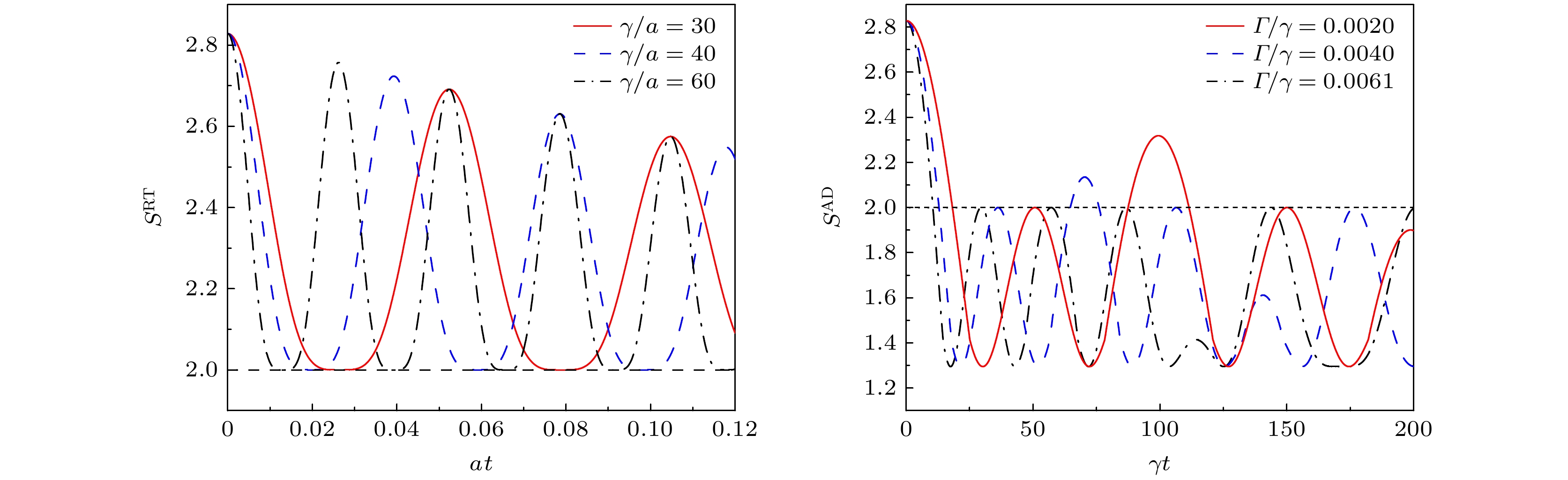
图 1 Werner态在RT噪声境中的量子非局域关联检验情况 (a) 当保真度$ F = 1 $时, 不同参数$\gamma /a$下$S_{}^{{\text{RT}}}$随$at$的变化曲线; (b) 当固定环境参数为$\gamma /a = 40$时, 不同F下的$S_{}^{{\text{RT}}}$随$at$的变化曲线
Fig. 1. Quantum non-local correlation testing of Werner state in RT noise environment: (a) $S_{}^{{\text{RT}}}$ versus evolution time $at$ under different $\gamma /a$ when $ F = 1 $; (b) $S_{}^{{\text{RT}}}$ versus evolution time $at$ under different fidelities when $\gamma /a = 40$
图 2 RT噪声环境中${F_{\min }}$随$\gamma /a$的变换关系曲线
Fig. 2. ${F_{\min }}$ versus $\gamma /a$ in RT noise environment.
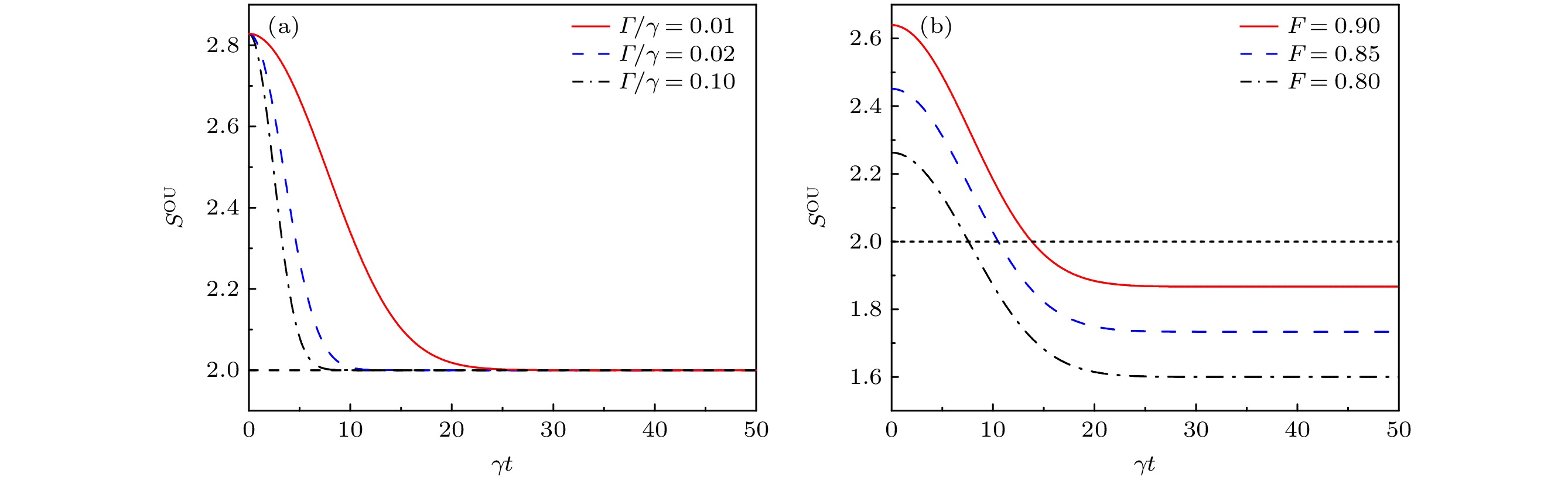
图 3 Werner态在OU噪声境中的量子非局域关联检验情况 (a) 当保真度$ F = 1 $时, 不同环境参数$\varGamma /\gamma $下的$ S_{}^{{\text{OU}}} $随$\gamma t$的变化曲线; (b) 当固定$\varGamma /\gamma = 0.01$时, 不同F参数下的$ S_{}^{{\text{OU}}} $随$\gamma t$的变化曲线
Fig. 3. Quantum non-local correlation testing of Werner state in OU noise environment: (a) $ S_{}^{{\text{OU}}} $ versus evolution time $\gamma t$ under different $\varGamma /\gamma $ when $ F = 1 $; (b) $S_{}^{{\text{OU}}}$ versus evolution time $\gamma t$ under different fidelities when $\varGamma /\gamma = 0.01$.
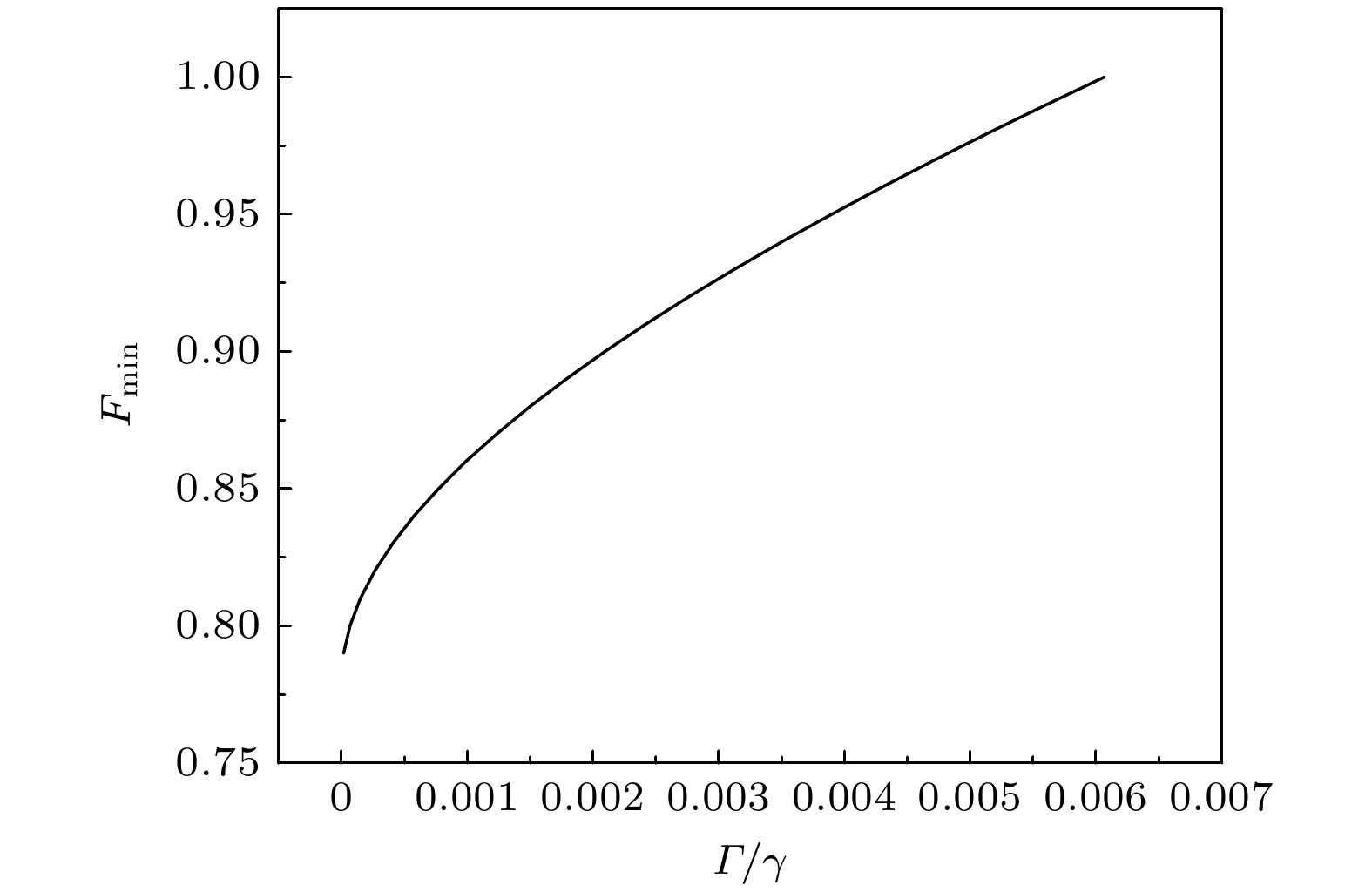
图 4 OU噪声环境中$\gamma {t_{\max }}$随$\varGamma /\gamma $, F的变化关系曲线(a)不同F下, $\gamma {t_{\max }}$随$\varGamma /\gamma $的变化曲线; (b) 不同$\varGamma /\gamma $下, $\gamma {t_{\max }}$随F的变化曲线
Fig. 4. $\gamma {t_{\max }}$ versus $\varGamma /\gamma $ and F respectively in OU noise environment: (a) $\gamma {t_{\max }}$ versus $\varGamma /\gamma $ under different F; (b) $\gamma {t_{\max }}$ versus F under different $\varGamma /\gamma $.
图 5 Werner态在振幅阻尼环境中的量子非局域关联检验情况 (a) 当保真度$ F = 1 $时, 不同$\varGamma /\gamma $参数下的$S_{}^{{\text{AD}}}$随演化时间$\gamma t$的变化曲线; (b) 当$\varGamma /\gamma = 0.0020$时, 不同F下的$S_{}^{{\text{AD}}}$随演化时间$\gamma t$的变化曲线
Fig. 5. Quantum non-local correlation testing of Werner state in amplitude damping environment: (a) $S_{}^{{\text{AD}}}$ versus evolution time $\gamma t$ under different $\varGamma /\gamma $ when $ F = 1 $; (b) $S_{}^{{\text{AD}}}$ versus evolution time $\gamma t$ under different fidelities when $\varGamma /\gamma = 0.0020$.
图 6 振幅阻尼环境中${F_{\min }}$随$\varGamma /\gamma $的变化关系曲线
Fig. 6. ${F_{\min }}$ versus $\varGamma /\gamma $ in amplitude damping environment.
图 7 振幅阻尼环境中$\gamma {t_{\max }}$随$\varGamma /\gamma $, F的变化关系曲线(a) 不同F下, $\gamma {t_{\max }}$随$\varGamma /\gamma $的变化曲线; (b) 不同$\varGamma /\gamma $下, $\gamma {t_{\max }}$随F的变化曲线
Fig. 7. $\gamma {t_{\max }}$ versus $\varGamma /\gamma $ and F respectively in amplitude damping environment: (a) $\gamma {t_{\max }}$ versus $\varGamma /\gamma $ under different F; (b) $\gamma {t_{\max }}$ versus F under different $\varGamma /\gamma $.
-
[1] Einstein A, Podolsky B, Rosen N 1935 Phys. Rev. Lett. 47 777
Google Scholar
[2] Gisin N, Ribordy G, Tittel W, Zbinden H 2002 Rev. Mod. Phys. 74 145
Google Scholar
[3] Bennett C H, Wiesner S J 1992 Phys. Rev. Lett. 69 2881
Google Scholar
[4] Bennett C H, Brassard G, Crépeau C, Jozsa R, Peres A, Wootters W K 1993 Phys. Rev. Lett. 70 1895
Google Scholar
[5] Bell J S 1964 Physics 1 195
Google Scholar
[6] Clauser J F, Horne M A, Shimony A, Holt R A 1969 Phys. Rev. Lett. 23 880
Google Scholar
[7] Horodecki R, Horodecki P, Horodecki M, Horodecki K 2009 Rev. Mod. Phys. 81 865
Google Scholar
[8] Collins D, Gisin N 2004 J. Phys. A: Math. Gen. 37 1775
Google Scholar
[9] Greenberger D M, Horne M A, Shimony A, Zeilinger A 1990 Am. J. Phys. 58 1131
Google Scholar
[10] Hardy L 1993 Phys. Rev. Lett. 71 1665
Google Scholar
[11] 胡强, 曾柏云, 辜鹏宇, 贾欣燕, 樊代和 2022 71 070301
Google Scholar
Hu Q, Zeng B Y, Gu P Y, Jia X Y, Fan D H 2022 Acta Phys. Sin. 71 070301
Google Scholar
[12] 曾柏云, 辜鹏宇, 蒋世民, 贾欣燕, 樊代和 2023 72 050301
Google Scholar
Zeng B Y, Gu P Y, Jiang S M, Jia X Y, Fan D H 2023 Acta Phys. Sin. 72 050301
Google Scholar
[13] Rivas Á, Huelga S F, Plenio M B 2014 Rep. Prog. Phys. 77 094001
Google Scholar
[14] Breuer H P, Laine E M, Piilo J, Vacchini B 2016 Rev. Mod. Phys. 88 021002
Google Scholar
[15] de Vicente J I, Spee C, Sauerwein D, Kraus B 2017 Phys. Rev. A 95 012323
Google Scholar
[16] Li L, Hall M J W, Wiseman H M 2018 Phys. Rep. 759 1
Google Scholar
[17] Weissman M B 1988 Rev. Mod. Phys. 60 537
Google Scholar
[18] Mi X, Cady J V, Zajac D M, Deelman P W, Petta J R 2017 Science 355 156
Google Scholar
[19] Groeblacher S, Trubarov A, Prigge N, Cole G D, Aspelmeyer M, Eisert J 2015 Nat. Commun. 6 7606
Google Scholar
[20] Potočnik A, Bargerbos A, Schröder F A Y N, Khan S A, Collodo M C, Gasparinetti S, Salathé Y, Creatore C, Eichler C, Türeci H E, Chin A W, Wallraff A 2018 Nat. Commun. 9 904
Google Scholar
[21] Haikka P, McEndoo S, De Chiara G, Palma G M, Maniscalco S 2011 Phys. Rev. A 84 031602
Google Scholar
[22] Utagi S, Srikanth R, Banerjee S 2020 Sci. Rep. 10 15049
Google Scholar
[23] Naikoo J, Banerjee S, Chandrashekar C M 2020 Phys. Rev. A 102 062209
Google Scholar
[24] Yu T, Eberly J 2007 Quantum Inf. Comput. 7 459
Google Scholar
[25] Kraus K 1971 Ann. Phys. 64 311
Google Scholar
[26] Rivas Á, Huelga S F, Plenio M B 2010 Phys. Rev. Lett. 105 050403
Google Scholar
[27] Breuer H P, Laine E M, Piilo J 2009 Phys. Rev. Lett. 103 210401
Google Scholar
[28] Pinto J P, Karpat G, Fanchini F F 2013 Phys. Rev. A. 88 034304
Google Scholar
[29] Yu T, Eberly J 2010 Opt. Commun. 283 676
Google Scholar
[30] Bellomo B, Franco R L, Compagno G 2007 Phys. Rev. Lett. 99 160502
Google Scholar
[31] Horodecki R, Horodecki P, Horodecki M 1995 Phys. Lett. A 200 340
Google Scholar
下载:
计量
- 文章访问数: 580
- PDF下载量: 40
- 被引次数: 0
