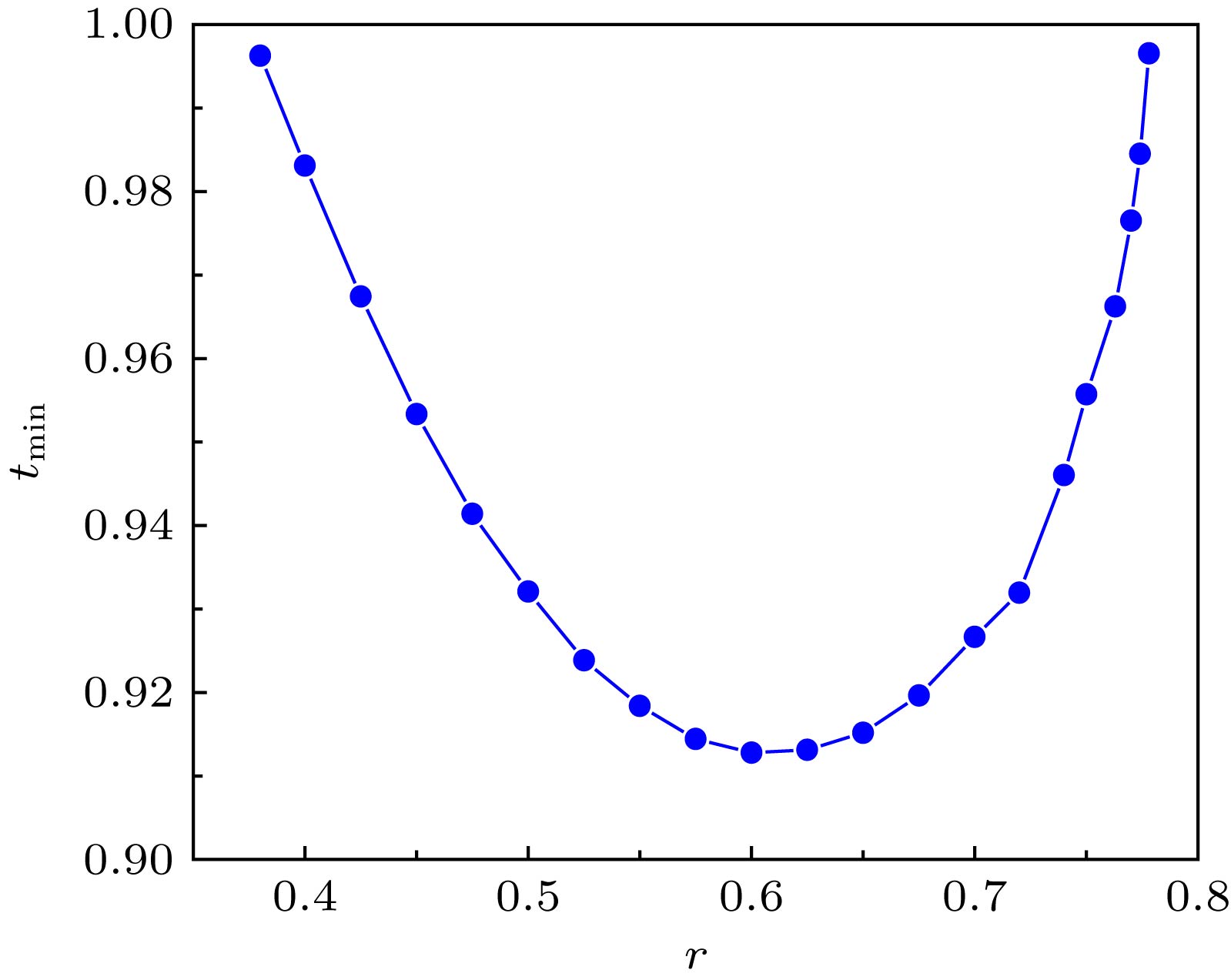
-
Quantum nonlocality is an important phenomenon predicted by quantum mechanics. It is also one of the most important characteristics that quantum theory is different from classical theory. Therefore, it is of great significance to test the quantum nonlocality with higher successful probability. In this paper, a testing logic based on Hardy-type paradox is proposed and its applicability is proved. Such a logic can be used to test the quantum nonlocality for both the quantum mixed state and the quantum pure state with a high successful probability. It is found that, for quantum pure states, the probability of successfully testing the quantum nonlocality first increases and then decreases with the increase of entanglement degree of quantum states. The maximum successful probability of the testing the quantum pure state is over 39%. Furthermore, taking the Werner-like state, a quantum mixed state for example, the high successful probability of testing the quantum nonlocality is investigated by using the proposed logic. It is found that with the increase of the purity of the quantum mixed state, the successful probability of testing the quantum nonlocal correlation will increase. Finally, the conditions and the range of testing quantum nonlocality with high successful probability for Werner states are given. It is found that for r = 0.599997, the Werner-like quantum mixed state has a maximum range (i.e.
${\rm Tr}({{\rho}^2}) \geqslant 0.874696$ ) of successfully testing the quantum nonlocality.-
Keywords:
- quantum nonlocality /
- Hardy-type paradox /
- quantum mixed state
[1] Einstein A, Podolsky B, Rosen N 1935 Phys. Rev. 47 777
Google Scholar
[2] Bell J S 1964 Physics 1 195
Google Scholar
[3] Clauser J F, HorneM A, Shimony A, Holt R A 1969 Phys. Rev. Lett. 23 880
Google Scholar
[4] Aspect A, Grangier P, Roger G 1981 Phys. Rev. Lett. 47 460
Google Scholar
[5] Greeberger D M, Horne M A, Shimony A, Zeilinger A 1990 Am. J. Phys. 58 1131
Google Scholar
[6] Hardy L 1993 Phys. Rev. Lett. 71 1665
Google Scholar
[7] Mermin N 1995 Ann. N. Y. Acad. Sci. 755 616
Google Scholar
[8] Boschi D, Branca S, de Martini F, Hardy L 1997 Phys. Rev. Lett. 79 2755
Google Scholar
[9] Torgerson J R, Branning D, Monken C H, Mandel L 1995 Phys. Lett. A 204 323
Google Scholar
[10] Fedrizzi A, Almeida M P, Broome M A, White A G, Barbieri M 2011 Phys. Rev. Lett. 106 200402
Google Scholar
[11] White A G, James D F V, Eberhard P H, Kwiat P G 1999 Phys. Rev. Lett. 83 3103
Google Scholar
[12] Chen L, Romero J 2012 Opt. Express 20 21687
Google Scholar
[13] Chen L X, Zhang W H, Wu Z W, Wang J K, Fickler R, Karimi E 2017 Phys. Rev. A 96 022115
Google Scholar
[14] Vallone G, Gianani I, Inostroza E B, Saavedra C, Lima G, Cabello A, Mataloni P 2011 Phys. Rev. A 83 042105
Google Scholar
[15] Cereceda J L 2004 Phys. Lett. A 327 433
Google Scholar
[16] Jiang S H, Xu Z P, Su H Y, Pati A K, Chen J L 2018 Phys. Rev. Lett. 120 050403
Google Scholar
[17] Chen J L, Cabello A, Xu Z P, Su H Y, Wu C, Kwek L C 2013 Phys.Rev. A 88 062116
Google Scholar
[18] Ghirardi G, Marinatto L 2006 Phys. Rev. A 73 032102
Google Scholar
[19] Ghirardi G, Marinatto L 2006 Phys. Rev. A 74 062107
Google Scholar
[20] Fan D H, Dai M C, Guo W J, Wei L F 2017 Chin. Phys. B 26 040302
Google Scholar
[21] 范洪义, 楼森岳, 潘孝胤, 笪诚 2014 63 190302
Google Scholar
Fan H Y, Lou S Y, Pan X Y, Da C 2014 Acta Phys. Sin. 63 190302
Google Scholar
[22] 石名俊, 杜江峰, 朱栋培, 阮图南 2000 49 1912
Shi M J, Du J F, Zhu D P, Ruan T N 2000 Acta Phys. Sin. 49 1912
[23] Werner R F 1989 Phys. Rev. A 40 4277
Google Scholar
[24] Yang M, Meng H X, Zhou J, Xu Z P, Xiao Y, Sun K, Chen J L, Xu J S, Li C F, Guo G C 2019 Phys. Rev. A 99 032103
Google Scholar
-
图 1
${H_{\max }}$ 随r的变化Figure 1. Relationship between
${H_{\max }}$ and r.
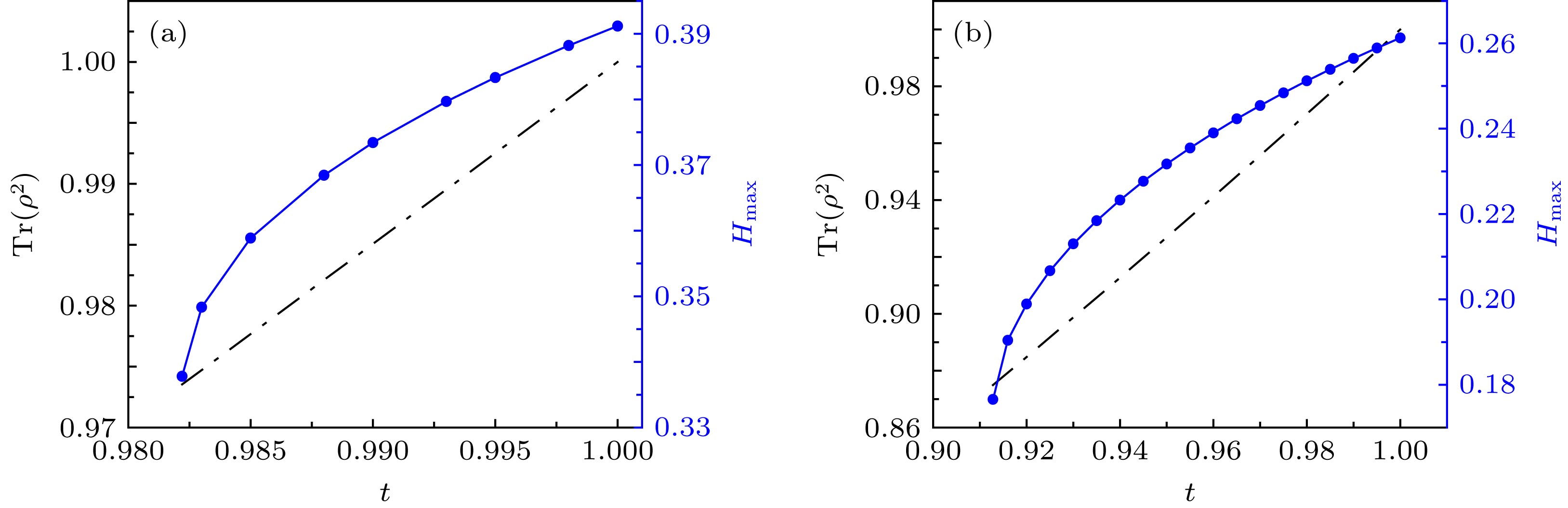
图 2
${\rm Tr}({\rho ^2})$ 以及${H_{\max }}$ 随t参数的变化关系 (a)$r = 0.773066$ 的情况; (b)$r = 0.599997$ 的情况; 其中蓝色实线表示${H_{\max }}$ 随t的变化关系, 对应于右边纵坐标; 黑色点化线表示${\rm Tr}({\rho ^2})$ 随t的变化关系, 对应于左边纵坐标Figure 2. Relationship between
${\rm Tr}({\rho ^2})$ and${H_{\max }}$ with t. The blue solid line means${H_{\max }}$ vs. t, using the right longitudinal coordinates. The black dot dash line means${\rm Tr}({\rho ^2})$ vs. t using the left longitudinal coordinates. Fig.2 (a) is the situation of$r = 0.773066$ and Fig.2 (b) is the situation of r = 0.599997.
图 3
${t_{\min }}$ 随r的变化Figure 3. Relationship between
${t_{\min }}$ and r. -
[1] Einstein A, Podolsky B, Rosen N 1935 Phys. Rev. 47 777
Google Scholar
[2] Bell J S 1964 Physics 1 195
Google Scholar
[3] Clauser J F, HorneM A, Shimony A, Holt R A 1969 Phys. Rev. Lett. 23 880
Google Scholar
[4] Aspect A, Grangier P, Roger G 1981 Phys. Rev. Lett. 47 460
Google Scholar
[5] Greeberger D M, Horne M A, Shimony A, Zeilinger A 1990 Am. J. Phys. 58 1131
Google Scholar
[6] Hardy L 1993 Phys. Rev. Lett. 71 1665
Google Scholar
[7] Mermin N 1995 Ann. N. Y. Acad. Sci. 755 616
Google Scholar
[8] Boschi D, Branca S, de Martini F, Hardy L 1997 Phys. Rev. Lett. 79 2755
Google Scholar
[9] Torgerson J R, Branning D, Monken C H, Mandel L 1995 Phys. Lett. A 204 323
Google Scholar
[10] Fedrizzi A, Almeida M P, Broome M A, White A G, Barbieri M 2011 Phys. Rev. Lett. 106 200402
Google Scholar
[11] White A G, James D F V, Eberhard P H, Kwiat P G 1999 Phys. Rev. Lett. 83 3103
Google Scholar
[12] Chen L, Romero J 2012 Opt. Express 20 21687
Google Scholar
[13] Chen L X, Zhang W H, Wu Z W, Wang J K, Fickler R, Karimi E 2017 Phys. Rev. A 96 022115
Google Scholar
[14] Vallone G, Gianani I, Inostroza E B, Saavedra C, Lima G, Cabello A, Mataloni P 2011 Phys. Rev. A 83 042105
Google Scholar
[15] Cereceda J L 2004 Phys. Lett. A 327 433
Google Scholar
[16] Jiang S H, Xu Z P, Su H Y, Pati A K, Chen J L 2018 Phys. Rev. Lett. 120 050403
Google Scholar
[17] Chen J L, Cabello A, Xu Z P, Su H Y, Wu C, Kwek L C 2013 Phys.Rev. A 88 062116
Google Scholar
[18] Ghirardi G, Marinatto L 2006 Phys. Rev. A 73 032102
Google Scholar
[19] Ghirardi G, Marinatto L 2006 Phys. Rev. A 74 062107
Google Scholar
[20] Fan D H, Dai M C, Guo W J, Wei L F 2017 Chin. Phys. B 26 040302
Google Scholar
[21] 范洪义, 楼森岳, 潘孝胤, 笪诚 2014 63 190302
Google Scholar
Fan H Y, Lou S Y, Pan X Y, Da C 2014 Acta Phys. Sin. 63 190302
Google Scholar
[22] 石名俊, 杜江峰, 朱栋培, 阮图南 2000 49 1912
Shi M J, Du J F, Zhu D P, Ruan T N 2000 Acta Phys. Sin. 49 1912
[23] Werner R F 1989 Phys. Rev. A 40 4277
Google Scholar
[24] Yang M, Meng H X, Zhou J, Xu Z P, Xiao Y, Sun K, Chen J L, Xu J S, Li C F, Guo G C 2019 Phys. Rev. A 99 032103
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 6433
- PDF Downloads: 59
- Cited By: 0
