Effects of graphene size and arrangement on crack propagation of graphene/aluminum composites

Wei Ning; Zhao Si-Han; Li Zhi-Hui; Ou Bing-Xian; Hua An-Ping; Zhao Jun-Hua

doi:10.7498/aps.71.20212203

Abstract

Aluminum-based composite material is one of the most important candidate materials in the mechanical industry and aerospace engineering due to its light weight and high strength. Graphene is an ideal reinforcement for composite materials for its excellent mechanical properties. Till-now, the contribution of graphene sheets in the process of crack propagation in composites is not clear. In present work, the effects of graphene size and distribution in graphene/aluminum composites are explored using molecular dynamics simulation methods. It is found that when the length of graphene flake is less than 3.35 nm, the generated sub-cracks in the composite is benefit to the crack propagation. This effect reduces the mechanical properties of composite. When the length of graphene flake is greater than 3.35 nm, graphene sheet impedes the crack propagation and dislocates slip at sub-cracks. In addition, the distribution of graphene flakes angle changes the crack propagation path. Our findings also provide insights into ways to optimize mechanical properties of graphene/aluminum composites.

Keywords:

Authors and contacts

1.
Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment and Technology, Jiangnan University, Wuxi 214122, China
2.
Aerodynamics Research and Development Center, Mianyang 621000, China
3.
National Laboratory for Computational Fluid Dynamics, Beijing 100191, China
4.
National Graphene Products Quality Supervision and Inspection Center, Special Equipment Safety Supervision Inspenction Institute of Jiangsu Provicne, Wuxi 214174, China

Corresponding author: Li Zhi-Hui, zhli0097@x263.net ; Zhao Jun-Hua, junhua.zhao@163.com

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 11502217), and the Manned Space Engineering Technology “Development of Large-scale Spacecraft Flight and Reentry Surveillance and Prediction System”, China (Grant No. 2020-ZKZX-5011).

FullText HTML : translate this paragraph

References

[1]	Singh S, Garg M, Batra N K 2015 Tribol. Trans. 58 758 Google Scholar
[2]	Hu Z, Tong G, Lin D, Chen C, Guo H, Xu J, Zhou L 2016 Mater. Sci. Technol. 32 930
[3]	Jayendra B, Sumanth D, Dinesh G, Rao M V 2020 Mater. Today:Proc. 21 1104 Google Scholar
[4]	Zhang X, Zhao N, He C 2020 Prog. Mater. Sci. 113 100672 Google Scholar
[5]	Novoselov K S, Fal'ko V I, Colombo L, Gellert P R, Schwab M G, Kim K 2012 Nature 490 192 Google Scholar
[6]	Dai Z, Hou Y, Sanchez D A, Wang G, Brennan C J, Zhang Z, Liu L, Lu N 2018 Phys. Rev. Lett. 121 266101 Google Scholar
[7]	Dai Z, Liu L, Zhang Z 2019 Adv. Mater. 31 1805417 Google Scholar
[8]	范冰冰, 郭焕焕, 李稳, 贾瑜, 张锐 2013 62 148101 Google Scholar Fan B-B, Guo H-H, Li W, Jia Y, Zhang R 2013 Acta Phys. Sin. 62 148101 Google Scholar
[9]	Stankovich S, Dikin D A, Dommett G H, Kohlhaas K M, Zimney E J, Stach E A, Piner R D, Nguyen S T, Ruoff R S 2006 Nature 442 282 Google Scholar
[10]	Zhang P, Ma L, Fan F, Zeng Z, Peng C, Loya P E, Liu Z, Gong Y, Zhang J, Zhang X, Ajayan P M, Zhu T, Lou J 2014 Nat. Commun. 5 3782 Google Scholar
[11]	Yang Z, Wang D, Lu Z, Hu W 2016 Appl. Phys. Lett. 109 191909 Google Scholar
[12]	Galashev A Y, Rakhmanova O R 2020 Phys. Lett. A 384 126790 Google Scholar
[13]	Wegst U G, Bai H, Saiz E, Tomsia A P, Ritchie R O 2015 Nat. Mater. 14 23 Google Scholar
[14]	Zhang Y, Li X 2017 Nano Lett. 17 6907 Google Scholar
[15]	Li Z, Guo Q, Li Z, Fan G, Xiong D B, Su Y, Zhang J, Zhang D 2015 Nano Lett. 15 8077 Google Scholar
[16]	Kim Y, Lee J, Yeom M S, Shin J W, Kim H, Cui Y, Kysar J W, Hone J, Jung Y, Jeon S, Han S M 2013 Nat. Commun. 4 2114 Google Scholar
[17]	Zhou X, Liu X, Shang J, Yang Q 2020 Mech. Mater. 148 103530 Google Scholar
[18]	Zhu J Q, Yang Q S, Liu X 2019 Key Eng. Mater. 804 1 Google Scholar
[19]	Muller S E, Santhapuram R R, Nair A K 2018 Comput. Mater. Sci. 152 341 Google Scholar
[20]	Su Y, Xu S 2016 Mater. Sci. Eng. , A 678 153 Google Scholar
[21]	Qiu R Z, Li C C, Fang T H 2017 Phys. Scr. 92 085702 Google Scholar
[22]	Akbarian S, Dehghani K 2020 Int. J. Fatigue 135 105570 Google Scholar
[23]	Plimpton S 1995 J. Comput. Phys. 117 1 Google Scholar
[24]	Wang P, Yang X, Tian X 2015 J. Mater. Res. 30 709 Google Scholar
[25]	Zhang C, Lu C, Pei L, Li J, Wang R, Tieu K 2019 Carbon 143 125 Google Scholar
[26]	Daw M S, Baskes M I 1984 Phys. Rev. B 29 6443 Google Scholar
[27]	Brenner D W, Shenderova O A, Harrison J A, Stuart S J, Ni B, Sinnott S B 2002 J. Phys. Condens. Matter 14 783 Google Scholar
[28]	Silvestre N, Faria B, Canongia Lopes J N 2014 Compos. Sci. Technol. 90 16 Google Scholar
[29]	汉芮岐, 宋海洋, 安敏荣, 李卫卫, 马佳丽 2021 70 066201 Google Scholar Han R Q, Song H Y, An M R, Li W W, Ma J L 2021 Acta Phys. Sin. 70 066201 Google Scholar
[30]	Kumar S 2018 Mater. Chem. Phys. 208 41 Google Scholar
[31]	Munilla J, Castro M, Carnicero A 2009 Phys. Rev. B 80 024109 Google Scholar
[32]	Kutana A, Giapis K P 2006 Phys. Rev. Lett. 97 245501 Google Scholar
[33]	Stukowski A 2010 Modell. Simul. Mater. Sci. Eng. 18 015012 Google Scholar
[34]	Kelchner C, Plimpton S, Hamilton J 2000 Phys. Rev. B 58 11085
[35]	Faken D, Jónsson H 1994 Comput. Mater. Sci. 2 279 Google Scholar
[36]	Stukowski A, Bulatov V V, Arsenlis A 2012 Modell. Simul. Mater. Sci. Eng. 20 085007 Google Scholar
[37]	Zheng Y G, Zhang H W, Chen Z, Lu C, Mai Y W 2009 Phys. Lett. A 373 570 Google Scholar
[38]	Rong Y, He H P, Zhang L, Li N, Zhu Y C 2018 Comput. Mater. Sci. 153 48 Google Scholar

Cited By

图 1 (a) Gr/Al复合材料的模型示意图; (b) 原子结构模型 (左侧为正视图, 右侧为剖视图)

Figure 1. (a) Geometrical representation of the simulated Gr/Al composite; (b) atomistic configurations for modeling (front view on the left and section view on the right).

DownLoad: Full-Size Img PowerPoint

图 2 石墨烯分布角度分别为 (a) θ = 0º, (b) θ = 45º和(c) θ = 90º的Gr/Al复合材料模型

Figure 2. Model of the Gr/Al composites with graphene orientations of (a) θ = 0º, (b) θ = 45º and (c) θ = 90º.

DownLoad: Full-Size Img PowerPoint

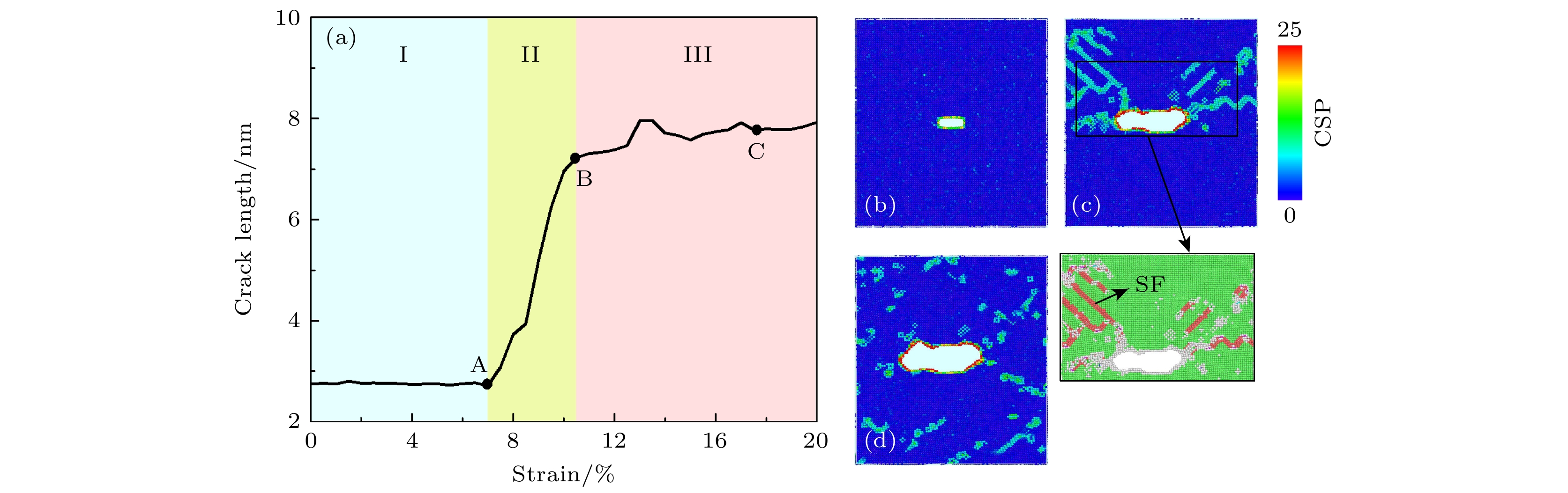
图 3 (a) 纯铝在单轴拉伸过程中的裂纹长度-应变曲线; (b)—(d) 为图3(a)中的A-C点CSP原子结构图 (插图中绿色原子为面心立方结构 (FCC), 红色原子为密排六方结构 (HCP), 白色原子为其他结构)

Figure 3. Uniaxial tensile process of pure Al: (a) Crack length-strain curve; (b)–(d) CSP morphology at points A-C correspongding to Fig. 3(a). (Atoms in the inset are colored by the CNA. Green atoms represent face-centered cubic structure (FCC), red atoms represent hexagonal closest packed structure (HCP) and white ones have OTHER structures.)

DownLoad: Full-Size Img PowerPoint

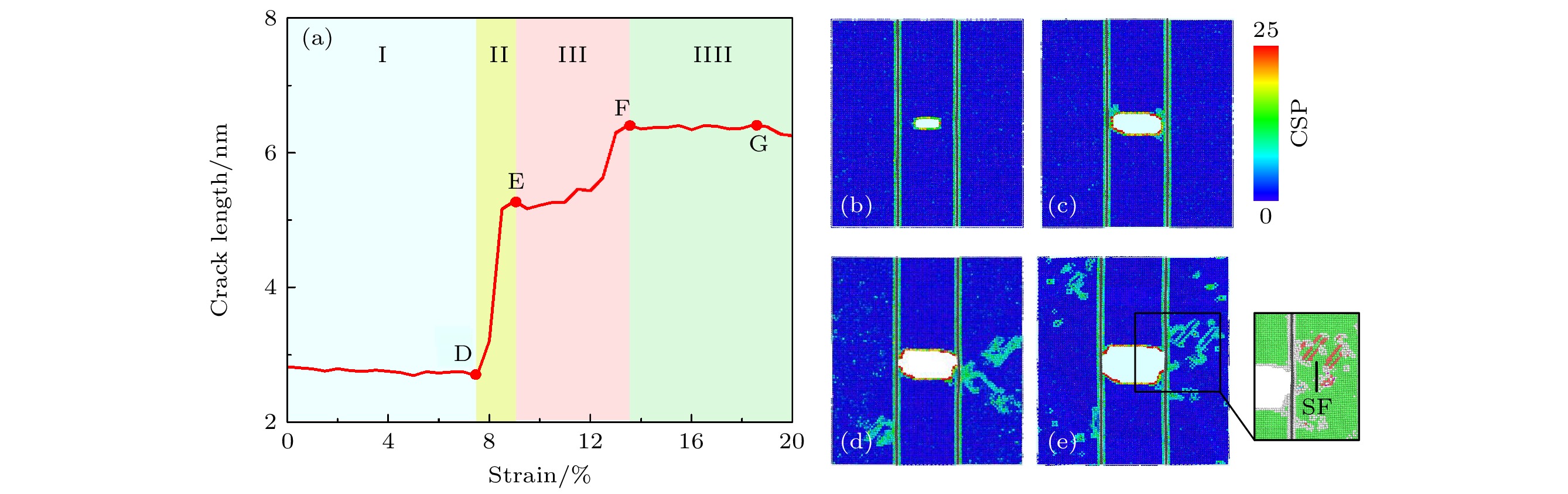
图 4 (a) p-Gr/Al的单轴拉伸过程裂纹长度-应变曲线; (b)—(e) 为图4(a)中的D-G点CSP原子结构图 (插图中绿色为FCC结构, 红色为HCP结构, 白色为OTHER结构, 黑色为C原子)

Figure 4. (a) Crack length-strain curve of p-Gr/Al under uniaxial tensile; (b)–(e) CSP morphology of p-Gr/Al corresponding to point D-G in Fig. 4(b). (Atoms in the inset are colored by the CNA. Green atoms have an FCC structure, red atoms have an HCP structure, white ones have other structures and black atoms are C atoms.)

DownLoad: Full-Size Img PowerPoint

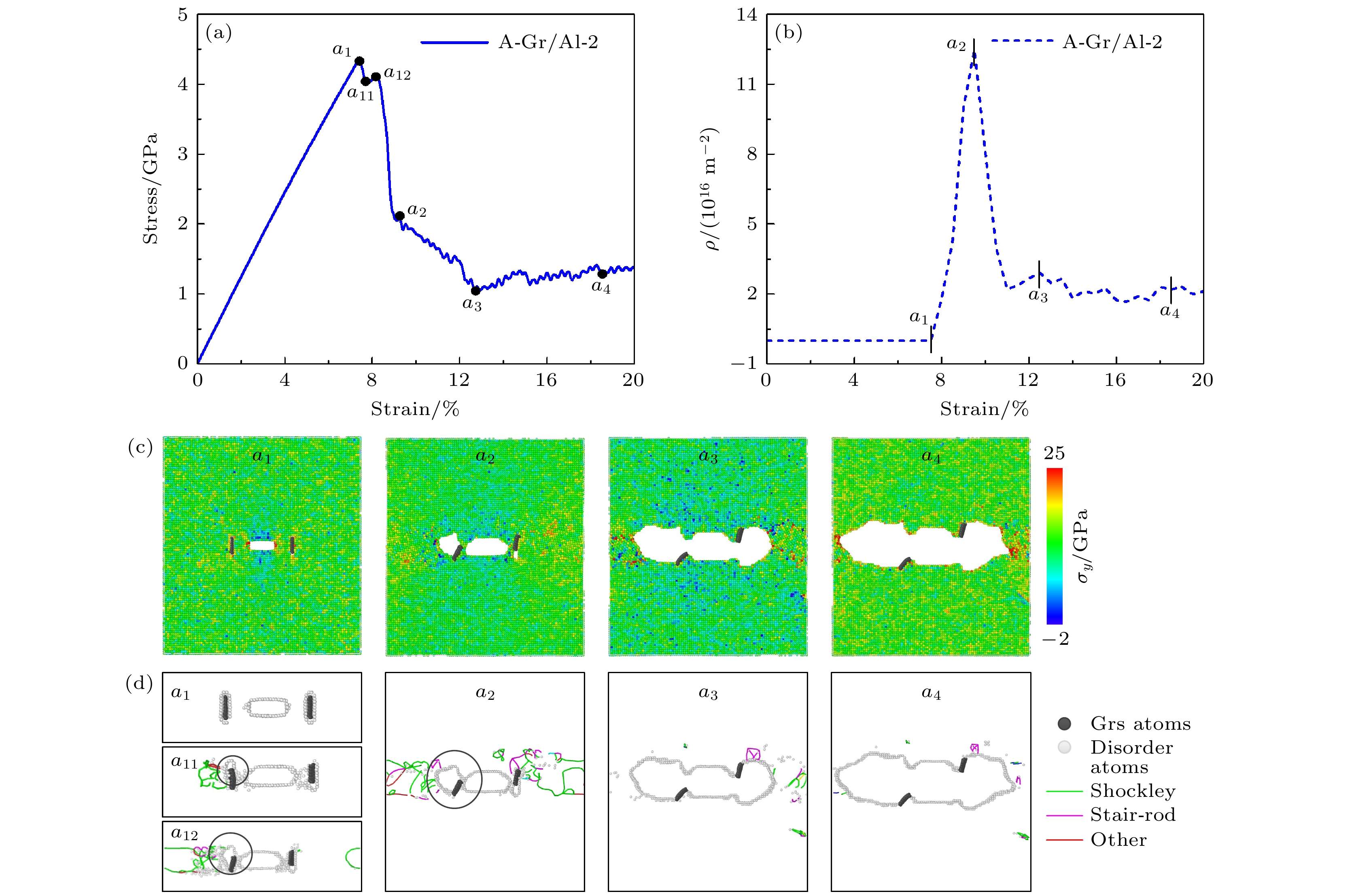
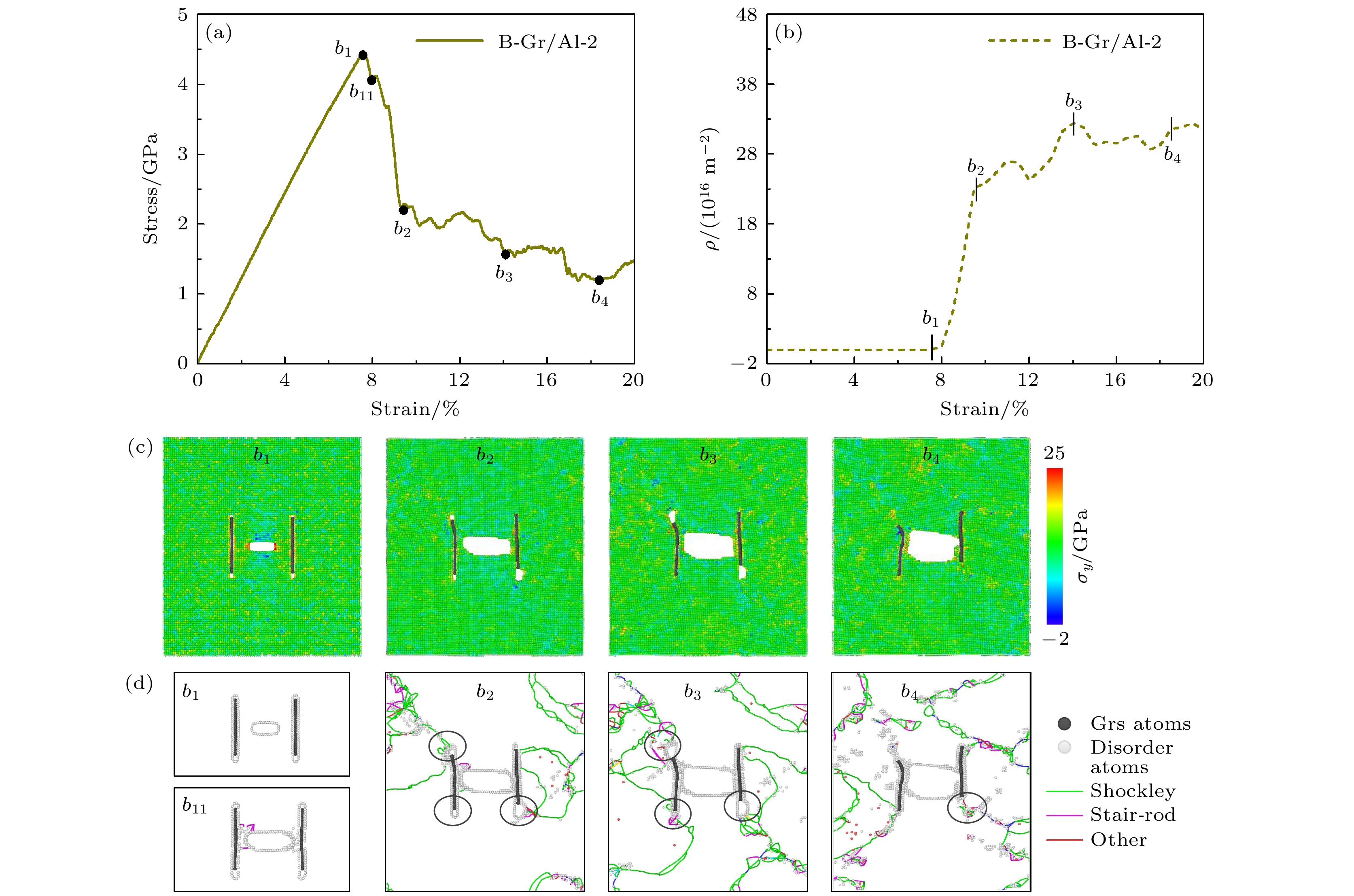
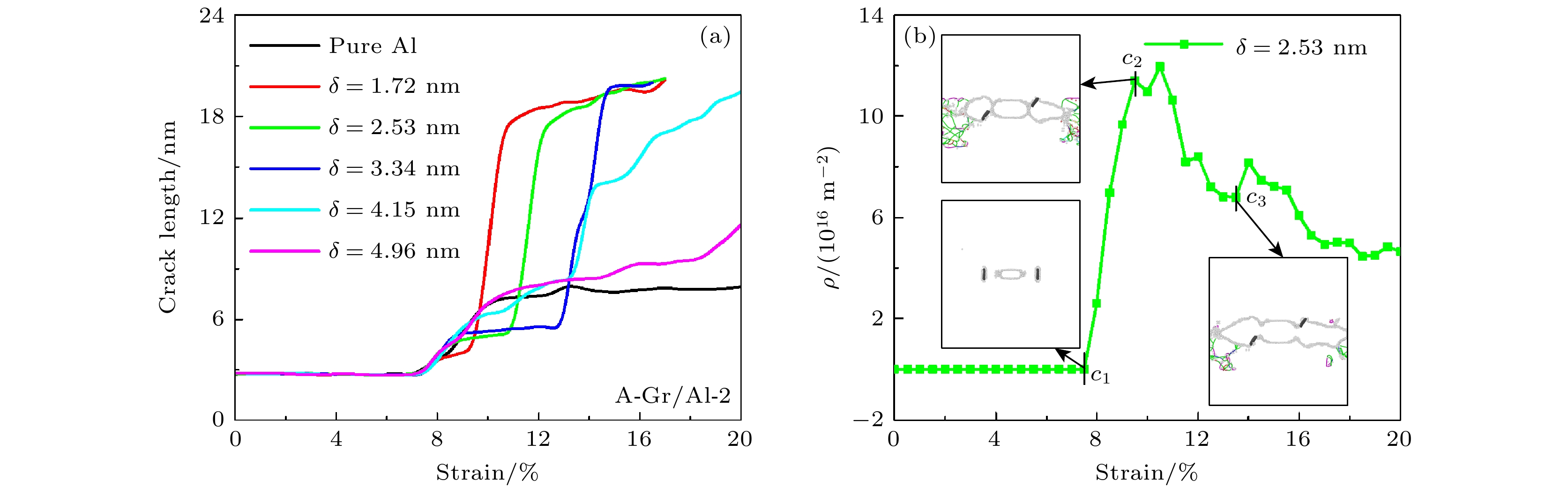
图 5 (a) 不同长度石墨烯Gr/Al复合材料的裂纹长度-应变曲线; (b) Gr/Al 复合材料的裂纹比随石墨烯嵌入长度的变化 (插图中A-Gr/Al和B-Gr/Al分别为A-Gr/Al-2和B-Gr/Al-2模型在20%时原子结构图)

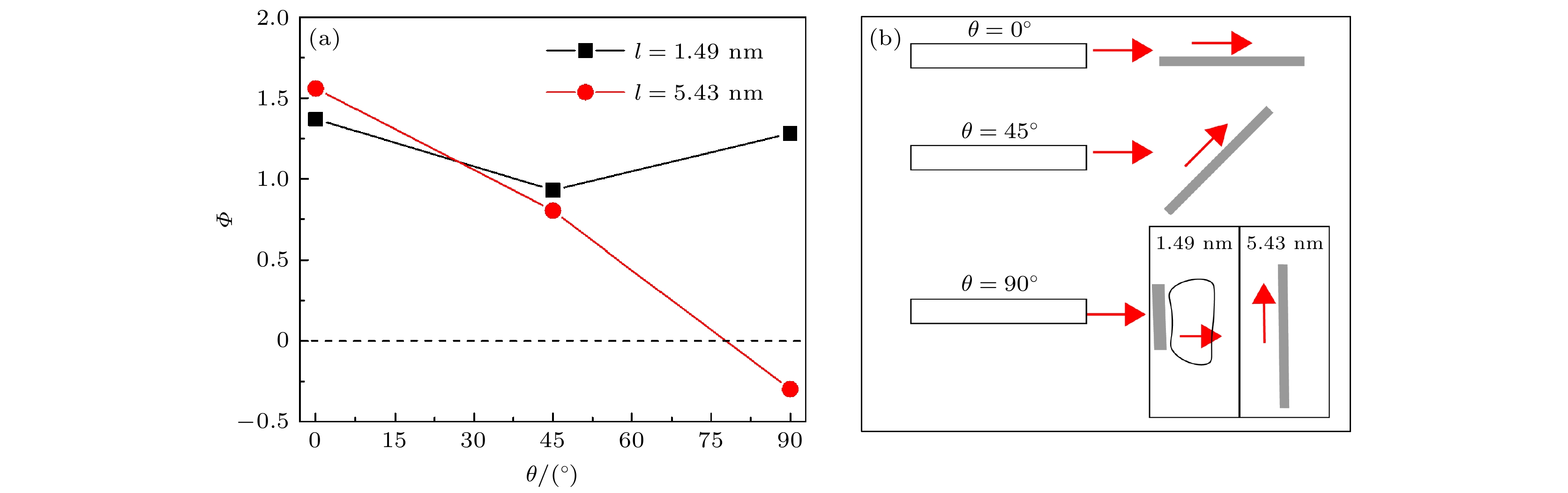
Figure 5. (a) Crack length-strain curves of Gr/Al composites with different Gr length; (b) relationship between the crack ratio of Gr/Al composites with different length of graphene (In the inset, A-Gr/Al and B-Gr/Al are atomic structure diagrams of A-Gr/Al-2 and B-Gr/Al-2 models at 20%, respectively).

DownLoad: Full-Size Img PowerPoint

图 6 A-Gr/Al-2的裂纹扩展　(a) 应力-应变曲线; (b) 位错密度-应变曲线; (c) a₁—a₄的σ_y瞬时应力分布图; (d) 位错线分布图

Figure 6. Evolution of A-Gr/Al-2 crack growth: (a) Stress-strain curve; (b) dislocation density-strain curve; (c) instantaneous stress distribution of σ_y for a₁–a₄; (d) distributions of dislocation lines.

DownLoad: Full-Size Img PowerPoint

图 7 B-Gr/Al-2的裂纹扩展运动　(a) 应力-应变曲线; (b) 位错密度-应变曲线; (c) b₁—b₄的瞬时σ_y应力图; (d) 位错线分布

Figure 7. Evolution of B-Gr/Al-2 crack growth behavior: (a) Stress-strain curve; (b) dislocation density-strain curve; (c) σ_ydistribution of b₁ to b₄; (d) distributions of dislocation lines.

DownLoad: Full-Size Img PowerPoint

图 8 (a) A-Gr/Al-2复合材料在δ为1.72—4.96 nm范围内的裂纹长度-应变曲线; (b) δ为2.53 nm的A-Gr/Al-2复合材料位错密度的演化

Figure 8. (a) Crack propagation in the δ range of 1.72—4.96 nm for A-Gr/Al-2 composites; (b) dislocation density evolution in the δ = 2.53 nm for A-Gr/Al-2 composite.

DownLoad: Full-Size Img PowerPoint

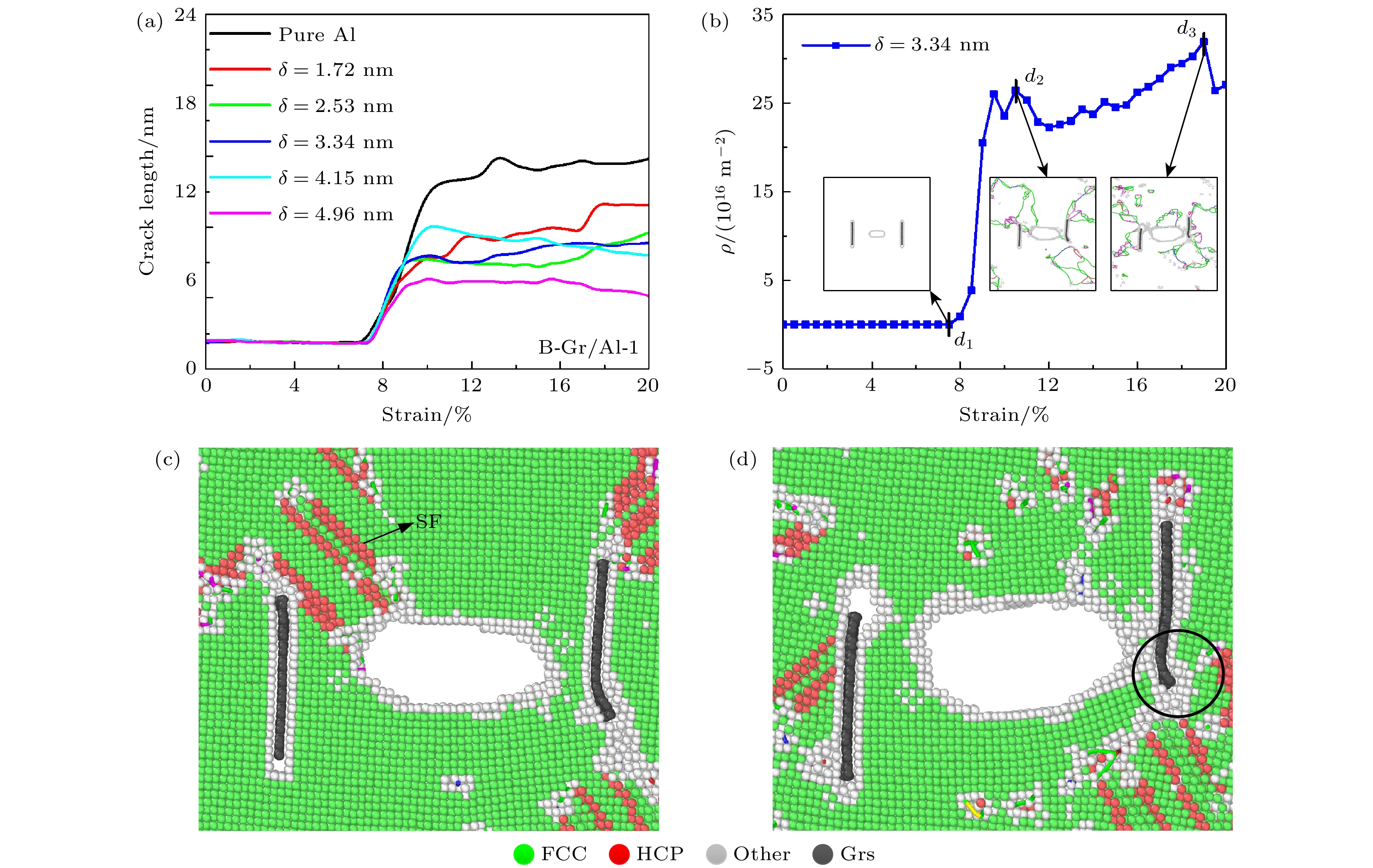
图 9 (a) B-Gr/Al-1复合材料在δ为1.72—4.96 nm范围内的裂纹长度-应变曲线; (b) δ为3.34 nm的B-Gr/Al-1复合材料位错密度的演化; (c), (d) 对应的d₂和d₃原子结构图

Figure 9. (a) Crack propagation in the δ range of 1.72—4.96 nm for B-Gr/Al-1; (b) dislocation density evolution in the δ = 3.34 nm for B-Gr/Al-1 composite; (c), (d) corresponding to d₂ and d₃ atomic structure.

DownLoad: Full-Size Img PowerPoint

图 10 石墨烯尺寸为1.49 nm的Gr/Al复合材料的裂纹扩展　(a) θ = 0º; (b) θ = 45º; (c) θ = 905

Figure 10. Crack propagation of Gr/Al composite with graphene length of 1.49 nm: (a) θ = 0º; (b) θ = 45º; (c) θ = 90º.

DownLoad: Full-Size Img PowerPoint

图 11 石墨烯尺寸为5.43 nm的Gr/Al复合材料的裂纹扩展　(a) θ = 0º; (b) θ = 45º; (c) θ = 90º

Figure 11. Crack propagation of Gr/Al composite with graphene length of 5.43 nm: (a) θ= 0º; (b) θ= 45º; (c) θ= 90º.

DownLoad: Full-Size Img PowerPoint

图 12 (a) 石墨烯尺寸为1.49 和5.43 nm的Gr/Al复合材料的裂纹比-分布角度曲线图; (b) 不同分布角度Gr/Al的裂纹扩展路径

Figure 12. (a) Crack ratio-direction angle curves of Gr/Al composites with graphene lengths of 1.49 and 5.43 nm; (b) crack propagation paths for different direction angle of Gr/Al composite.

DownLoad: Full-Size Img PowerPoint

表 1 不同模型的参数, 包括石墨烯长度 (l ) 和石墨烯与裂纹的相对距离 (δ)

Table 1. Parameters of different models including graphene length (l ) and the distance between graphene and crack (δ).

模型名称	l/nm	δ/nm	模型名称	l/nm	δ/nm
Pure Al	0	0	B-Gr/Al-2	5.43	1.72
A-Gr/Al-1	0.97	1.72	B-Gr/Al-3	7.53	1.72
A-Gr/Al-2	1.49	1.72—4.96	B-Gr/Al-4	9.92	1.72
A-Gr/Al-3	2.64	1.72	B-Gr/Al-5	15.22	1.72
A-Gr/Al-4	3.35	1.72	p-Gr/Al	20.25	1.72
B-Gr/Al-1	4.18	1.72—4.96

DownLoad: CSV

表 2 原子间Lennard-Jones (L-J)势函数参数值

Table 2. Lennard-Jones (L-J) potential parameter for atomic interactions

	相互作用的原子
L-J势函数参数	Al-Al^[31]	C-C^[32]	Al-C^[29,30]
σ/Å	2.6200	3.4070	3.0135
ε/eV	0.4157	0.00296	0.0351

DownLoad: CSV

map

[1]	Singh S, Garg M, Batra N K 2015 Tribol. Trans. 58 758 Google Scholar
[2]	Hu Z, Tong G, Lin D, Chen C, Guo H, Xu J, Zhou L 2016 Mater. Sci. Technol. 32 930
[3]	Jayendra B, Sumanth D, Dinesh G, Rao M V 2020 Mater. Today:Proc. 21 1104 Google Scholar
[4]	Zhang X, Zhao N, He C 2020 Prog. Mater. Sci. 113 100672 Google Scholar
[5]	Novoselov K S, Fal'ko V I, Colombo L, Gellert P R, Schwab M G, Kim K 2012 Nature 490 192 Google Scholar
[6]	Dai Z, Hou Y, Sanchez D A, Wang G, Brennan C J, Zhang Z, Liu L, Lu N 2018 Phys. Rev. Lett. 121 266101 Google Scholar
[7]	Dai Z, Liu L, Zhang Z 2019 Adv. Mater. 31 1805417 Google Scholar
[8]	范冰冰, 郭焕焕, 李稳, 贾瑜, 张锐 2013 62 148101 Google Scholar Fan B-B, Guo H-H, Li W, Jia Y, Zhang R 2013 Acta Phys. Sin. 62 148101 Google Scholar
[9]	Stankovich S, Dikin D A, Dommett G H, Kohlhaas K M, Zimney E J, Stach E A, Piner R D, Nguyen S T, Ruoff R S 2006 Nature 442 282 Google Scholar
[10]	Zhang P, Ma L, Fan F, Zeng Z, Peng C, Loya P E, Liu Z, Gong Y, Zhang J, Zhang X, Ajayan P M, Zhu T, Lou J 2014 Nat. Commun. 5 3782 Google Scholar
[11]	Yang Z, Wang D, Lu Z, Hu W 2016 Appl. Phys. Lett. 109 191909 Google Scholar
[12]	Galashev A Y, Rakhmanova O R 2020 Phys. Lett. A 384 126790 Google Scholar
[13]	Wegst U G, Bai H, Saiz E, Tomsia A P, Ritchie R O 2015 Nat. Mater. 14 23 Google Scholar
[14]	Zhang Y, Li X 2017 Nano Lett. 17 6907 Google Scholar
[15]	Li Z, Guo Q, Li Z, Fan G, Xiong D B, Su Y, Zhang J, Zhang D 2015 Nano Lett. 15 8077 Google Scholar
[16]	Kim Y, Lee J, Yeom M S, Shin J W, Kim H, Cui Y, Kysar J W, Hone J, Jung Y, Jeon S, Han S M 2013 Nat. Commun. 4 2114 Google Scholar
[17]	Zhou X, Liu X, Shang J, Yang Q 2020 Mech. Mater. 148 103530 Google Scholar
[18]	Zhu J Q, Yang Q S, Liu X 2019 Key Eng. Mater. 804 1 Google Scholar
[19]	Muller S E, Santhapuram R R, Nair A K 2018 Comput. Mater. Sci. 152 341 Google Scholar
[20]	Su Y, Xu S 2016 Mater. Sci. Eng. , A 678 153 Google Scholar
[21]	Qiu R Z, Li C C, Fang T H 2017 Phys. Scr. 92 085702 Google Scholar
[22]	Akbarian S, Dehghani K 2020 Int. J. Fatigue 135 105570 Google Scholar
[23]	Plimpton S 1995 J. Comput. Phys. 117 1 Google Scholar
[24]	Wang P, Yang X, Tian X 2015 J. Mater. Res. 30 709 Google Scholar
[25]	Zhang C, Lu C, Pei L, Li J, Wang R, Tieu K 2019 Carbon 143 125 Google Scholar
[26]	Daw M S, Baskes M I 1984 Phys. Rev. B 29 6443 Google Scholar
[27]	Brenner D W, Shenderova O A, Harrison J A, Stuart S J, Ni B, Sinnott S B 2002 J. Phys. Condens. Matter 14 783 Google Scholar
[28]	Silvestre N, Faria B, Canongia Lopes J N 2014 Compos. Sci. Technol. 90 16 Google Scholar
[29]	汉芮岐, 宋海洋, 安敏荣, 李卫卫, 马佳丽 2021 70 066201 Google Scholar Han R Q, Song H Y, An M R, Li W W, Ma J L 2021 Acta Phys. Sin. 70 066201 Google Scholar
[30]	Kumar S 2018 Mater. Chem. Phys. 208 41 Google Scholar
[31]	Munilla J, Castro M, Carnicero A 2009 Phys. Rev. B 80 024109 Google Scholar
[32]	Kutana A, Giapis K P 2006 Phys. Rev. Lett. 97 245501 Google Scholar
[33]	Stukowski A 2010 Modell. Simul. Mater. Sci. Eng. 18 015012 Google Scholar
[34]	Kelchner C, Plimpton S, Hamilton J 2000 Phys. Rev. B 58 11085
[35]	Faken D, Jónsson H 1994 Comput. Mater. Sci. 2 279 Google Scholar
[36]	Stukowski A, Bulatov V V, Arsenlis A 2012 Modell. Simul. Mater. Sci. Eng. 20 085007 Google Scholar
[37]	Zheng Y G, Zhang H W, Chen Z, Lu C, Mai Y W 2009 Phys. Lett. A 373 570 Google Scholar
[38]	Rong Y, He H P, Zhang L, Li N, Zhu Y C 2018 Comput. Mater. Sci. 153 48 Google Scholar

[1]	Xie JiaMiao, Li JingYang, Zhou JiaYi, Hao WenQian. Analysis of electrode crack propagation in solid oxide fuel cell with pre-crack. Acta Physica Sinica, 2024, 73(23): . doi: 10.7498/aps.73.20241176
[2]	Liu Qing-Yang, Xu Qing-Song, Li Rui. Effect of N-doping on tribological properties of graphene by molecular dynamics simulation. Acta Physica Sinica, 2022, 71(14): 146801. doi: 10.7498/aps.71.20212309
[3]	Ming Zhi-Fei, Song Hai-Yang, An Min-Rong. Mechanical behavior of graphene magnesium matrix composites based on molecular dynamics simulation. Acta Physica Sinica, 2022, 71(8): 086201. doi: 10.7498/aps.71.20211753
[4]	Han Rui-Qi, Song Hai-Yang, An Min-Rong, Li Wei-Wei, Ma Jia-Li. Simulation of interaction behavior between dislocation and graphene during nanoindentation of graphene/aluminum matrix nanocomposites. Acta Physica Sinica, 2021, 70(6): 066201. doi: 10.7498/aps.70.20201591
[5]	Li Xing-Xin, Li Si-Ping. Manipulations on mechanical properties of multilayer folded graphene by annealing temperature: a molecular dynamics simulation study. Acta Physica Sinica, 2020, 69(19): 196102. doi: 10.7498/aps.69.20200836
[6]	Shi Chao, Lin Chen-Sen, Chen Shuo, Zhu Jun. Molecular dynamics simulation of characteristic water molecular arrangement on graphene surface and wetting transparency of graphene. Acta Physica Sinica, 2019, 68(8): 086801. doi: 10.7498/aps.68.20182307
[7]	Wang Jun-Jun, Li Tao, Li Xiong-Ying, Li Hui. Wettability and morphology of liquid gallium on graphene surface. Acta Physica Sinica, 2018, 67(14): 149601. doi: 10.7498/aps.67.20172717
[8]	Bai Qing-Shun, Shen Rong-Qi, He Xin, Liu Shun, Zhang Fei-Hu, Guo Yong-Bo. Interface adhesion property between graphene film and surface of nanometric microstructure. Acta Physica Sinica, 2018, 67(3): 030201. doi: 10.7498/aps.67.20172153
[9]	Dong Ruo-Yu, Cao Peng, Cao Gui-Xing, Hu Guo-Jie, Cao Bing-Yang. DC electric field induced orientation of a graphene in water. Acta Physica Sinica, 2017, 66(1): 014702. doi: 10.7498/aps.66.014702
[10]	Yang Wen-Long, Han Jun-Sheng, Wang Yu, Lin Jia-Qi, He Guo-Qiang, Sun Hong-Guo. Molecular dynamics simulation on the glass transition temperature and mechanical properties of polyimide/functional graphene composites. Acta Physica Sinica, 2017, 66(22): 227101. doi: 10.7498/aps.66.227101
[11]	Lin Wen-Qiang, Xu Bin, Chen Liang, Zhou Feng, Chen Jun-Lang. Molecular dynamics simulations of the adsorption of bisphenol A on graphene oxide. Acta Physica Sinica, 2016, 65(13): 133102. doi: 10.7498/aps.65.133102
[12]	Li Gui-Rong, Wang Hong-Ming, Li Pei-Si, Gao Lei-Zhang, Peng Cong-Xiang, Zheng Rui. Mechanism of dislocation kinetics under magnetoplastic effect. Acta Physica Sinica, 2015, 64(14): 148102. doi: 10.7498/aps.64.148102
[13]	Wang Hong-Ming, Li Pei-Si, Zheng Rui, Li Gui-Rong, Yuan Xue-Ting. Mechanism of high pulsed magnetic field treatment of the plasticity of aluminum matrix composites. Acta Physica Sinica, 2015, 64(8): 087104. doi: 10.7498/aps.64.087104
[14]	Qin Ye-Hong, Tang Chao, Zhang Chun-Xiao, Meng Li-Jun, Zhong Jian-Xin. Molecular dynamics study of ripples in graphene monolayer on silicon surface. Acta Physica Sinica, 2015, 64(1): 016804. doi: 10.7498/aps.64.016804
[15]	Xu Jun, Xiao Xiao-Chun, Pan Yi-Shan, Ding Xin. Granular coal crack propagation study under uniaxial compression based on J integral. Acta Physica Sinica, 2014, 63(21): 214602. doi: 10.7498/aps.63.214602
[16]	Ye Zhen-Qiang, Cao Bing-Yang, Guo Zeng-Yuan. Study on thermal characteristics of phonons in graphene. Acta Physica Sinica, 2014, 63(15): 154704. doi: 10.7498/aps.63.154704
[17]	Sun Wei-Feng, Wang Xuan. Molecular dynamics simulation study of polyimide/copper-nanoparticle composites. Acta Physica Sinica, 2013, 62(18): 186202. doi: 10.7498/aps.62.186202
[18]	Dai Chun-Juan, Liu Xi-Qin, Liu Zi-Li, Liu Bo-Lu. The Monte Carlo simulation of neutron shielding performance of boron carbide reinforced with aluminum composites. Acta Physica Sinica, 2013, 62(15): 152801. doi: 10.7498/aps.62.152801
[19]	Han Tong-Wei, He Peng-Fei. Molecular dynamics simulation of relaxation properties of graphene sheets. Acta Physica Sinica, 2010, 59(5): 3408-3413. doi: 10.7498/aps.59.3408
[20]	Li Rui, Hu Yuan-Zhong, Wang Hui, Zhang Yu-Jun. Molecular dynamics simulation of motion of single-walled carbon nanotubes on graphite substrate. Acta Physica Sinica, 2006, 55(10): 5455-5459. doi: 10.7498/aps.55.5455

Catalog

Vol. 71, Issue 13 - 2022-07-05

Metrics

Abstract views: 5129
PDF Downloads: 109
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板