-
退火是石墨烯宏观组装材料常用的制备工艺之一, 广泛用于其性能的调控. 在石墨烯基材料中, 石墨烯片层由于其自身的二维特性通常在微纳米尺度下呈现出多层折叠的结构. 然而这种微观结构对材料力学性能退火调控的影响仍未得到充分的了解. 为了阐明多层折叠石墨烯力学性能与退火温度间的调控关系, 基于分子动力学模拟研究了材料弹性模量、拉伸强度、极限应变以及断裂韧性等关键力学性能参数随退火温度的变化规律, 进而结合观察微观结构的演化过程揭示了性能调控现象的物理机制. 结果表明: 更高的退火温度将增强多层折叠石墨烯的弹性模量与拉伸强度, 但同时削弱了其极限应变, 并且其断裂韧性能够在一定退火温度范围内实现强化. 研究发现, 以上力学性能的调控作用归因于更高的退火温度将造成更加密集的层间交联, 从而增强了折叠区域层间界面的相互作用, 并限制了折叠结构的形态展开, 致使结构破坏模式发生转变.Annealing is a commonly used fabrication technology of graphene-assembled materials, which serves as an efficient method to control material properties. In graphene-assembled materials, the multilayer folded configuration of graphene has been widely observed due to the two dimensional characteristic of graphene. However, the manipulation on the mechanical properties of graphene-assembled materials by annealing has not been fully understood yet, especially considering the effect of folded microstructures. In this paper, we focus on the effect of annealing temperature on the mechanical properties of multilayer folded graphene. The dependences of elastic modulus, tensile strength, ultimate strain and fracture toughness on the annealing temperature have been systematically studied by molecular dynamics simulations. Moreover, the mechanisms behind the manipulations by annealing temperature have been revealed combining the structural evolutions obtained from the simulations. Our results indicate that the multilayer folded graphene after annealing under higher temperature exhibits significant reinforcement on its elastic modulus and tensile strength, while its ultimate strain drops instead. The fracture toughness is enhanced only within a certain range of annealing temperature. The controllable mechanical properties are attributed to the formation of interlayer covalent bonds between carbon atoms belonging to adjacent layers during the annealing processing. With the annealing temperature increases, more interlayer crosslinks are observed from simulations, which greatly strengthens the interlayer interaction. For the cases with lower annealing temperature, the folded graphene can be unfolded easily then finally flattened under tensile stretch, and the structural failure originates from the interlayer slippage in the folded area. However, for the cases with higher annealing temperature, the unfolding deformation is prevented since the folded graphene is blocked by much denser interlayer crosslinks, and the origins of structural failure transforms to the intralayer fracture in graphene plane. Considering the intralayer covalent bond interaction is far more powerful than the interlayer van der Waals interaction, the higher annealing temperature will bring higher elastic modulus and tensile strength due to the change on the structural failure mode, but it will sacrifice the ductility at the same time due to the blocked unfolding process of folded area. It is confirmed in our study that the annealing is an effective approach for the synthetic modulation on the stiffness, strength, ductility and toughness of multilayer folded graphene.
-
Keywords:
- multilayer folded graphene /
- annealing temperature /
- mechanical property /
- molecular dynamics simulation
[1] Wei Y J, Yang R G 2019 Natl. Sci. Rev. 6 324
Google Scholar
[2] L ee, C, Wei X D, Kysar J W, Hone J 2008 Science 321 385
Google Scholar
[3] Cao K, Feng S Z, Han Y, Gao L B, Ly T H, Xu Z P, Lu Y 2020 Nat. Commun. 11 284
Google Scholar
[4] Shim J, Yun J M, Yun T, Kim P, Lee K E, Lee W J, R R, Pine D J, Yi G R, Kim S O 2014 Nano Lett. 14 1388
Google Scholar
[5] Li P, Yang M C, Liu Y J, Qin H S, Liu J R, Xu Z, Liu Y L, Meng F X, Lin J H, Wang F, Gao C 2020 Nat. Commun. 11 2645
Google Scholar
[6] Xiao P, Gu J C, Wan C J, Wang S, He J, Zhang J W, Huang Y J, Kuo S W, Chen T 2016 Chem. Mater. 28 7125
Google Scholar
[7] Xu Z, Gao C 2015 Mater. Today 18 480
Google Scholar
[8] Zhang X, Zhong L, Mateos A, Kudo A, Vyatskikh A, Gao H J, Greer J R, Li X Y 2019 Nat. Nanotechnol. 14 762
Google Scholar
[9] Zhong L, Gao H J, Li X Y 2020 Extreme Mech. Lett. 37 100699
Google Scholar
[10] Peng L, Xu Z, Liu Z, Guo Y, Li P, Gao C 2017 Adv. Mater. 29 1700589
Google Scholar
[11] Zhang J, Xiao J L, Meng X H, Monroe C, Huang Y G, Zuo J M 2010 Phys. Rev. Lett. 104 166805
Google Scholar
[12] 邓剑锋, 李慧琴, 于帆, 梁齐 2020 69 076802
Google Scholar
Deng J F, Li H Q, Yu F, Liang Q 2020 Acta Phys. Sin. 69 076802
Google Scholar
[13] Jia X Z, Liu Z, Gao E L 2020 npj Comput. Mater. 6 13
Google Scholar
[14] Ahn Y, Kim J, Ganorkar S, Kim Y H, Kim S I 2016 Mater. Express 6 69
Google Scholar
[15] Grimm S, Schweiger M, Eigler S, Zaumseil J 2016 J. Phys. Chem. C 120 3036
Google Scholar
[16] Liu Y J, Liang C, Wei A R, Jiang Y Q, Tian Q S, Wu Y, Xu Z, Li Y F, Guo F, Yang Q Y, Gao W W, Wang H T, Gao C 2018 Mater. Today Nano 3 1
Google Scholar
[17] Ruiz L, Xia W J, Meng Z X, Keten S 2015 Carbon 82 103
Google Scholar
[18] Shen Y K, Wu H A 2012 Appl. Phys. Lett. 100 101909
Google Scholar
[19] Liu F, Song S Y, Xue D F, Zhang H J 2012 Adv. Mater. 24 1089
Google Scholar
[20] Ugeda M M, Fernández-Torre D, Brihuega I, Pou P, Martínez-Galera A J, Pérez R, Gómez-Rodríguez J M 2011 Phys. Rev. Lett. 107 116803
Google Scholar
[21] Stuart S J, Tutein A B, Harrison J A 2000 J. Chem. Phys. 112 6472
Google Scholar
[22] 何欣, 白清顺, 白锦轩 2016 65 116101
Google Scholar
He X, Bai Q S, Bai J X 2016 Acta Phys. Sin. 65 116101
Google Scholar
[23] Plimpton S J 1995 J. Comput. Phys. 117 1
Google Scholar
[24] He Z Z, Zhu Y B, Xia J, Wu H A 2019 J. Mech. Phys. Solid 133 103706
Google Scholar
[25] Wu K J, Song Z Q, He L H, Ni Y 2018 Nanoscale 10 556
Google Scholar
[26] Zhang T, Li X Y, Gao H J 2014 Extreme Mech. Lett. 1 3
Google Scholar
[27] Zhang P, Ma L L, Fan F F, Zeng Z, Peng C, Loya P E, Liu Z, Gong Y J, Zhang J N, Zhang X X, Ajayan P M, Zhu T 2014 Nat. Commun. 5 3782
Google Scholar
[28] Wang G R, Dai Z H, Wang Y L, Tan P H, Liu L Q, Xu Z P, Wei Y G, Huang R, Zhang Z 2017 Phys. Rev. Lett. 119 036101
Google Scholar
-
图 1 多层折叠石墨烯的分子动力学模型
Fig. 1. Model of multilayer folded graphene for molecular dynamics simulation.
图 2 不同退火温度Ta处理时温度随模拟时间的变化
Fig. 2. Evolutions of temperature with simulation time for different annealing temperature Ta.
图 3 不同退火温度Ta下多层折叠石墨烯的拉伸应力应变曲线
Fig. 3. Stress-strain curves of multilayer folded graphene under different annealing temperature Ta.
图 4 不同退火温度处理下多层折叠石墨烯力学性能的变化 (a) 弹性模量; (b) 拉伸强度; (c) 拉伸极限应变; (d) 断裂韧性
Fig. 4. Dependence of mechanical properties of multilayer folded graphene on the annealing temperature: (a) Elastic modulus; (b) tensile strength; (c) ultimate tensile strain; (d) fracture toughness.
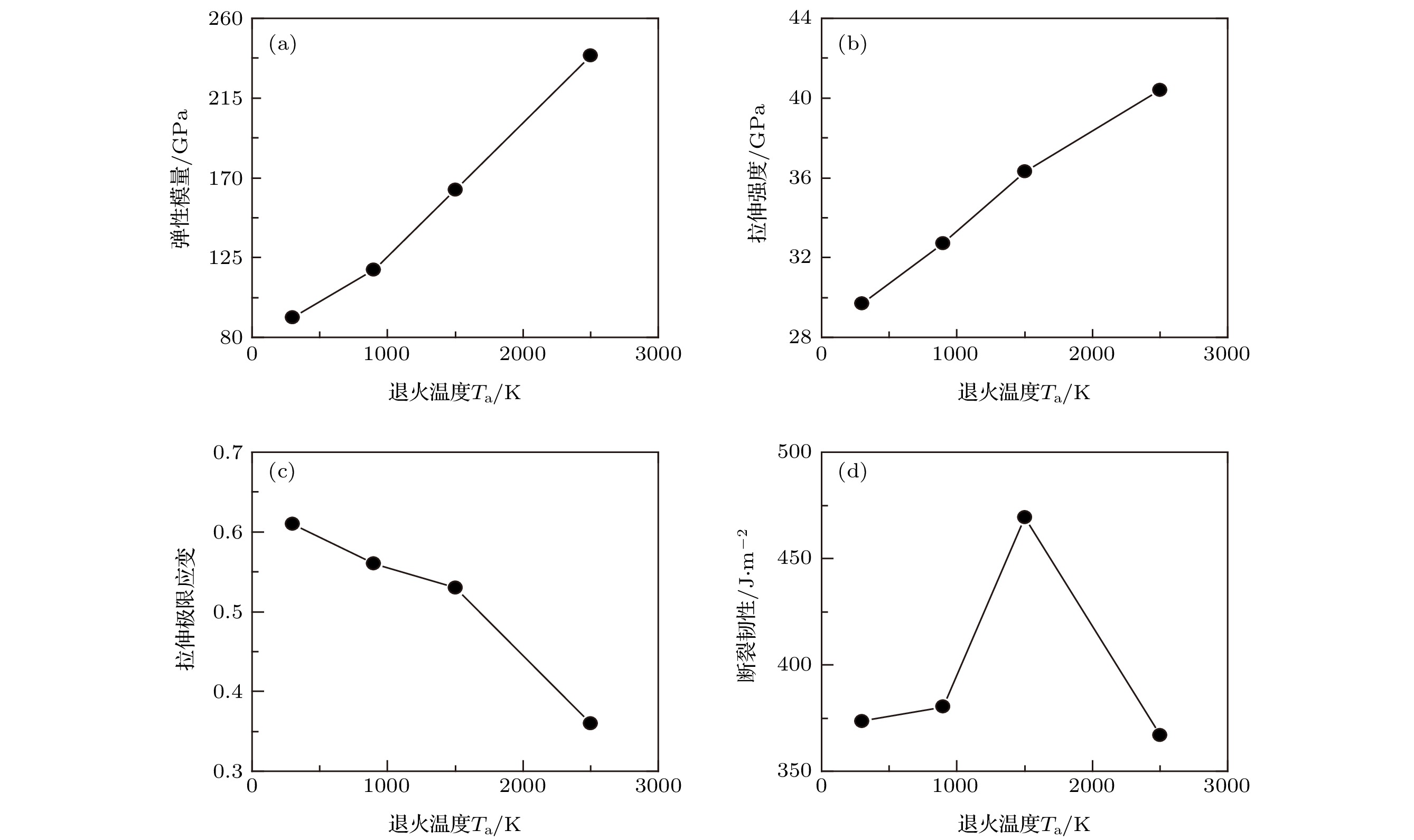
图 5 (a), (b) 不同退火温度处理下平整带缺陷多层石墨烯弹性模量与拉伸强度的变化; (c), (d) 不同退火温度处理下折叠无缺陷多层石墨烯弹性模量与拉伸强度的变化
Fig. 5. (a), (b) Dependence of elastic modulus and tensile strength on the annealing temperature, respectively, for the flat multilayer graphene with vacancy defects; (c), (d) dependence of elastic modulus and tensile strength on the annealing temperature, respectively, for the folded multilayer graphene without defects.
图 6 退火温度Ta为300 K下多层折叠石墨烯的微观结构演化
Fig. 6. Atomic structural evolution of multilayer folded graphene under the annealing temperature Ta at 300 K.
图 7 退火温度Ta为1500 K下多层折叠石墨烯的微观结构演化
Fig. 7. Atomic structural evolution of multilayer folded graphene under the annealing temperature Ta at 1500 K.
图 8 退火温度Ta为2500 K下多层折叠石墨烯的微观结构演化
Fig. 8. Atomic structural evolution of multilayer folded graphene under the annealing temperature Ta at 2500 K.
-
[1] Wei Y J, Yang R G 2019 Natl. Sci. Rev. 6 324
Google Scholar
[2] L ee, C, Wei X D, Kysar J W, Hone J 2008 Science 321 385
Google Scholar
[3] Cao K, Feng S Z, Han Y, Gao L B, Ly T H, Xu Z P, Lu Y 2020 Nat. Commun. 11 284
Google Scholar
[4] Shim J, Yun J M, Yun T, Kim P, Lee K E, Lee W J, R R, Pine D J, Yi G R, Kim S O 2014 Nano Lett. 14 1388
Google Scholar
[5] Li P, Yang M C, Liu Y J, Qin H S, Liu J R, Xu Z, Liu Y L, Meng F X, Lin J H, Wang F, Gao C 2020 Nat. Commun. 11 2645
Google Scholar
[6] Xiao P, Gu J C, Wan C J, Wang S, He J, Zhang J W, Huang Y J, Kuo S W, Chen T 2016 Chem. Mater. 28 7125
Google Scholar
[7] Xu Z, Gao C 2015 Mater. Today 18 480
Google Scholar
[8] Zhang X, Zhong L, Mateos A, Kudo A, Vyatskikh A, Gao H J, Greer J R, Li X Y 2019 Nat. Nanotechnol. 14 762
Google Scholar
[9] Zhong L, Gao H J, Li X Y 2020 Extreme Mech. Lett. 37 100699
Google Scholar
[10] Peng L, Xu Z, Liu Z, Guo Y, Li P, Gao C 2017 Adv. Mater. 29 1700589
Google Scholar
[11] Zhang J, Xiao J L, Meng X H, Monroe C, Huang Y G, Zuo J M 2010 Phys. Rev. Lett. 104 166805
Google Scholar
[12] 邓剑锋, 李慧琴, 于帆, 梁齐 2020 69 076802
Google Scholar
Deng J F, Li H Q, Yu F, Liang Q 2020 Acta Phys. Sin. 69 076802
Google Scholar
[13] Jia X Z, Liu Z, Gao E L 2020 npj Comput. Mater. 6 13
Google Scholar
[14] Ahn Y, Kim J, Ganorkar S, Kim Y H, Kim S I 2016 Mater. Express 6 69
Google Scholar
[15] Grimm S, Schweiger M, Eigler S, Zaumseil J 2016 J. Phys. Chem. C 120 3036
Google Scholar
[16] Liu Y J, Liang C, Wei A R, Jiang Y Q, Tian Q S, Wu Y, Xu Z, Li Y F, Guo F, Yang Q Y, Gao W W, Wang H T, Gao C 2018 Mater. Today Nano 3 1
Google Scholar
[17] Ruiz L, Xia W J, Meng Z X, Keten S 2015 Carbon 82 103
Google Scholar
[18] Shen Y K, Wu H A 2012 Appl. Phys. Lett. 100 101909
Google Scholar
[19] Liu F, Song S Y, Xue D F, Zhang H J 2012 Adv. Mater. 24 1089
Google Scholar
[20] Ugeda M M, Fernández-Torre D, Brihuega I, Pou P, Martínez-Galera A J, Pérez R, Gómez-Rodríguez J M 2011 Phys. Rev. Lett. 107 116803
Google Scholar
[21] Stuart S J, Tutein A B, Harrison J A 2000 J. Chem. Phys. 112 6472
Google Scholar
[22] 何欣, 白清顺, 白锦轩 2016 65 116101
Google Scholar
He X, Bai Q S, Bai J X 2016 Acta Phys. Sin. 65 116101
Google Scholar
[23] Plimpton S J 1995 J. Comput. Phys. 117 1
Google Scholar
[24] He Z Z, Zhu Y B, Xia J, Wu H A 2019 J. Mech. Phys. Solid 133 103706
Google Scholar
[25] Wu K J, Song Z Q, He L H, Ni Y 2018 Nanoscale 10 556
Google Scholar
[26] Zhang T, Li X Y, Gao H J 2014 Extreme Mech. Lett. 1 3
Google Scholar
[27] Zhang P, Ma L L, Fan F F, Zeng Z, Peng C, Loya P E, Liu Z, Gong Y J, Zhang J N, Zhang X X, Ajayan P M, Zhu T 2014 Nat. Commun. 5 3782
Google Scholar
[28] Wang G R, Dai Z H, Wang Y L, Tan P H, Liu L Q, Xu Z P, Wei Y G, Huang R, Zhang Z 2017 Phys. Rev. Lett. 119 036101
Google Scholar
下载:
计量
- 文章访问数: 8990
- PDF下载量: 156
- 被引次数: 0
