Rotational electroosmotic slip flow of power-law fluid at high zeta potential in  variable-section microchannel

Zhang Tian-Ge; Ren Mei-Rong; Cui Ji-Feng; Chen Xiao-Gang; Wang Yi-Dan

doi:10.7498/aps.71.20212327

Abstract

In this paper we study the rotating electroosmotic flow of a power-law fluid with Navier slip boundary conditions under high zeta potential subjected to the action of a vertical magnetic field in a variable cross-section microchannel. Without using the Debye–Hückel linear approximation, the finite difference method is used to numerically calculate the potential distribution and velocity distribution of the rotating electroosmotic flow subjected to an external magnetic field. When the behavior index $n = 1$, the fluid obtained is a Newtonian fluid. The analysis results in this paper are compared with the analytical approximate solutions obtained in the Debye–Hückel linear approximation to prove the feasibility of the numerical method in this paper. In addition, the influence of behavior index n, Hartmann number Ha, rotation angular velocity $\Omega $, electric width K and slip parameters $\beta $ on the velocity distribution are discussed in detail. It is obtained that when the Hartmann number Ha > 1, the velocity decreases with the increase of the Hartmann number Ha; but when the Hartmann number Ha < 1, the magnitude of the x-direction velocity u increases with the augment of Ha.

Keywords:

Authors and contacts

College of Science, Inner Mongolia University of Technology, Hohhot 010051, China

Corresponding author: Chen Xiao-Gang, xiaogang_chen@imut.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 12062018, 12172333), the Young Talents of Science and Technology in Universities of Inner Mongolia Autonomous Region, China (Grant No. NJYT22075), and the Natural Science Foundation of Inner Mongolia, China (Grant No. 2020MS01015).

FullText HTML

References

[1]	Stone H A, Stroock A D, Ajdari A 2004 Annu. Rev. Fluid Mech. 36 381 Google Scholar
[2]	Patel M, Kruthiventi S S H, Kaushik P 2020 Colloids Surf. B 193 111058 Google Scholar
[3]	Srinivas, Bhadri 2016 Colloids Surf. A 492 144 Google Scholar
[4]	Nekoubin N 2018 J. Non-Newtonian Fluid Mech. 260 54 Google Scholar
[5]	Baños R D, Arcos J C, Bautista O, Méndez F, Merchán-Cruz E A 2021 J. Braz. Soc. Mech. Sci. 43 1 Google Scholar
[6]	Baños R, Arcos J, Bautista O, Méndez F 2020 Defect Diffus. Forum 399 92 Google Scholar
[7]	姜玉婷, 齐海涛 2015 64 174702 Google Scholar Jiang Y T, Qi H T 2015 Acta Phys. Sin. 64 174702 Google Scholar
[8]	Ajdari A 2002 Phys. Rev. E 65 16301 Google Scholar
[9]	Chang C C, Wang C Y 2011 Phys. Rev. E 84 056320 Google Scholar
[10]	Song J, Wang S W, Zhao M L, Li N 2020 Z. Naturforsch. A: Phys. Sci. 75 649 Google Scholar
[11]	Shit G C, Mondal A, Sinha A, Kundu P K 2016 Colloids Surf. A 489 249 Google Scholar
[12]	刘全生, 杨联贵, 苏洁 2013 62 144702 Google Scholar Liu Q S, Yang L G, Su J 2013 Acta Phys. Sin. 62 144702 Google Scholar
[13]	段娟, 陈耀钦, 朱庆勇 2016 65 034702 Google Scholar Duan J, Chen Y Q, Zhu Q Y 2016 Acta Phys. Sin. 65 034702 Google Scholar
[14]	Weston M C, Gerner M D, Fritsch I 2010 Anal. Chem. 82 3411 Google Scholar
[15]	Jian Y J, Chang L 2015 AIP Adv. 5 057121 Google Scholar
[16]	Xie Z Y, Jian Y J 2017 Colloids Surf. A 529 334 Google Scholar
[17]	Habib U, Hayat T, Ahmad S, Alhodaly M S 2021 Int. Commun. Heat Mass Transfer 122 105111 Google Scholar
[18]	Sarkar S, Ganguly S 2017 J. Non-Newtonian Fluid Mech. 250 18 Google Scholar
[19]	Yang C H, Jian Y J, Xie Z Y, Li F Q 2020 Micromachines 11 418 Google Scholar
[20]	Xie Z Y, Jian Y J 2017 Energy 139 1080 Google Scholar
[21]	Wang S W, Li N, Zhao M L, Azese M N 2018 Z. Naturforsch. A: Phys. Sci. 73 825 Google Scholar
[22]	Xie Z Y, Jian Y J 2014 Colloids Surf. A 461 231 Google Scholar
[23]	Bird R B, Armstrong R C, Hassager O, Curtiss C F, Middleman S 1978 Phys. Today 31 54 Google Scholar

Cited By

图 1 变截面微通道中流体流动示意图

Figure 1. Schematic view of the flow in a variable cross-section microchannel.

DownLoad: Full-Size Img PowerPoint

图 2 目前数值解与Chang和Wang^[9]解析解的比较, 其中 $ \beta = 0, $$ K = 30, $$\varOmega = 100{\text{ }}{\rm{rad}}/{\rm{s}}, {\text{ }}{\bar \psi _\omega } = 1{\text{ }}{\rm{V}}, {\text{ }}a = 0, {\text{ }}Ha = 0, {\text{ }}S = 0$

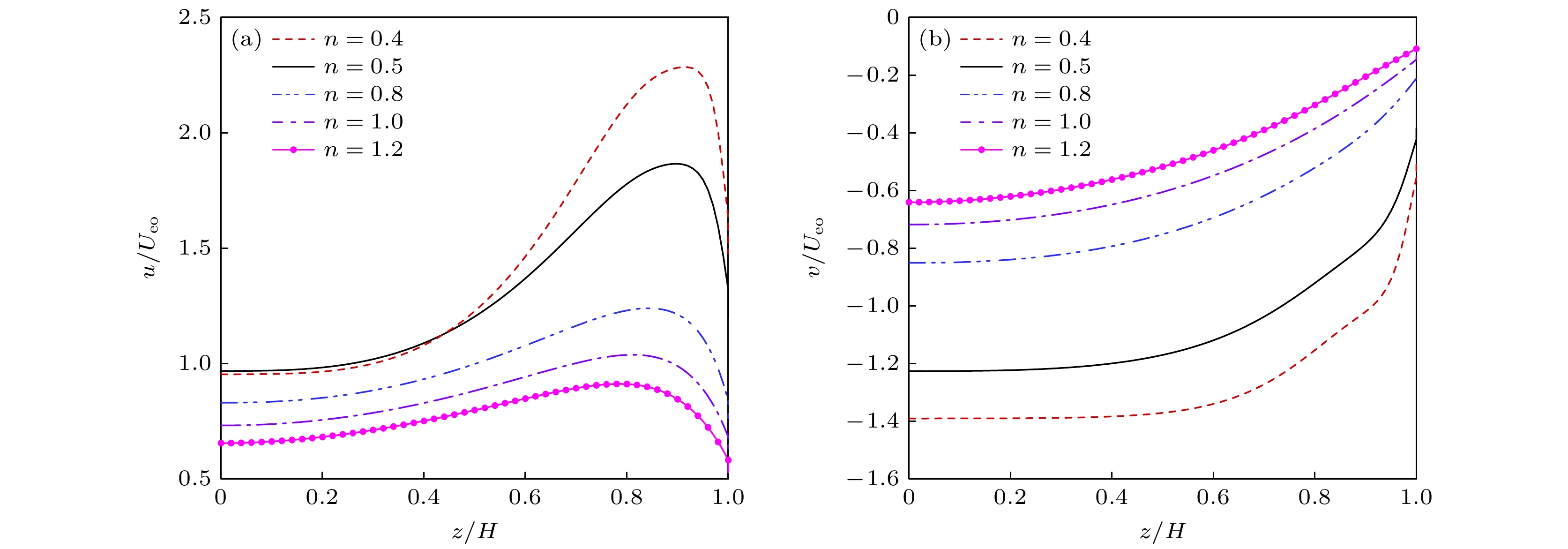
Figure 2. Comparison of the current numerical solution with the analytical solution of Chang and Wang ^[9], $ \beta = 0, $$ K = 30, $$\varOmega = 100{\text{ }}{\rm{rad}}/{\rm{s}}, {\text{ }}{\bar \psi _\omega } = 1{\text{ }}{\rm{V}}, {\text{ }}a = 0, {\text{ }}Ha = 0, {\text{ }}S = 0$

DownLoad: Full-Size Img PowerPoint

图 3 当无滑移边界条件时, 幂律流体行为指数n对外加磁场的旋转电渗流速度的影响, 其中$\beta = 0, {\text{ }}K = 10, {\text{ }}\varOmega = 100{\text{ }}{\rm{rad}}/{\rm{s}}, $ ${\text{ }}{\bar \psi _\omega } = 5 \;{\rm{V}}, {\text{ }}a = 0.05, {\text{ }}Ha = 1, {\text{ }}S = $1

Figure 3. When there is a no-slip boundary condition, the influence of power-law fluid behavior index n on rotating electroosmotic flow velocity with the external magnetic field, $\beta = 0, {\text{ }}K = 10, {\text{ }}\varOmega = 100{\text{ }}{\rm{rad}}/{\rm{s}}, {\text{ }}{\bar \psi _\omega } = 5 \;{\rm{V}}, {\text{ }}a = 0.05, {\text{ }}Ha = 1, {\text{ }}S = 1$

DownLoad: Full-Size Img PowerPoint

图 4 当存在滑移边界条件时, 幂律流体行为指数n对外加磁场的旋转电渗流速度的影响, 其中$ \beta = 0.1, {\text{ }}K = 10, {\text{ }}\varOmega = 100{\text{ }}{\rm{rad}}/{\rm{s}}, $ ${\text{ }}{\bar \psi _\omega } = 5{\text{ }}{\rm{V}}, {\text{ }}a = 0.05, {\text{ }}Ha = 1, {\text{ }}S =$1

Figure 4. When there is a slip boundary condition, the influence of the power-law fluid behavior index n on the rotating electroosmotic flow velocity with an external magnetic field, $\beta = 0.1, {\text{ }}K = 10, {\text{ }}\varOmega = 100{\text{ }}{\rm{rad}}/{\rm{s}}, {\text{ }}{\bar \psi _\omega } = 5{\text{ }}{\rm{V}}, {\text{ }}a = 0.05, {\text{ }}Ha = 1, {\text{ }}S = 1$

DownLoad: Full-Size Img PowerPoint

图 5 哈特曼数Ha对外加磁场的旋转电渗流速度的影响, 其中$ n = 0.8, {\text{ }}K = 10, $ $ {\text{ }}\beta = 0.1, {\text{ }}\varOmega = 100{\text{ }}{\rm{rad}}/{\rm{s}}, $ ${\text{ }}{\bar \psi _\omega } = 5{\text{ }}{\rm{V}}, {\text{ }}a = $$ 0.05, {\text{ }}S =$1

Figure 5. The influence of Hartmann number Ha on the velocity of rotating electroosmotic flow with external magnetic field, $ n = 0.8, {\text{ }}K = 10, $$ {\text{ }}\beta = 0.1, {\text{ }}\varOmega = 100{\text{ }}{\rm{rad}}/{\rm{s}}, {\text{ }}{\bar \psi _\omega } = 5{\text{ }}{\rm{V}}, {\text{ }}a = 0.05, {\text{ }}S = 1 $

DownLoad: Full-Size Img PowerPoint

图 6 哈特曼数Ha对外加磁场的旋转电渗流速度的影响, 其中$ n = 1.2, {\text{ }}K = 10, $ ${\text{ }}\beta = 0.1, {\text{ }}\varOmega = 100{\text{ }}{\rm{rad}}/{\rm{s}}, $ ${\bar \psi _\omega } = 5{\text{ }}{\rm{V}}, {\text{ }}a = $$ 0.05, {\text{ }}S =$1

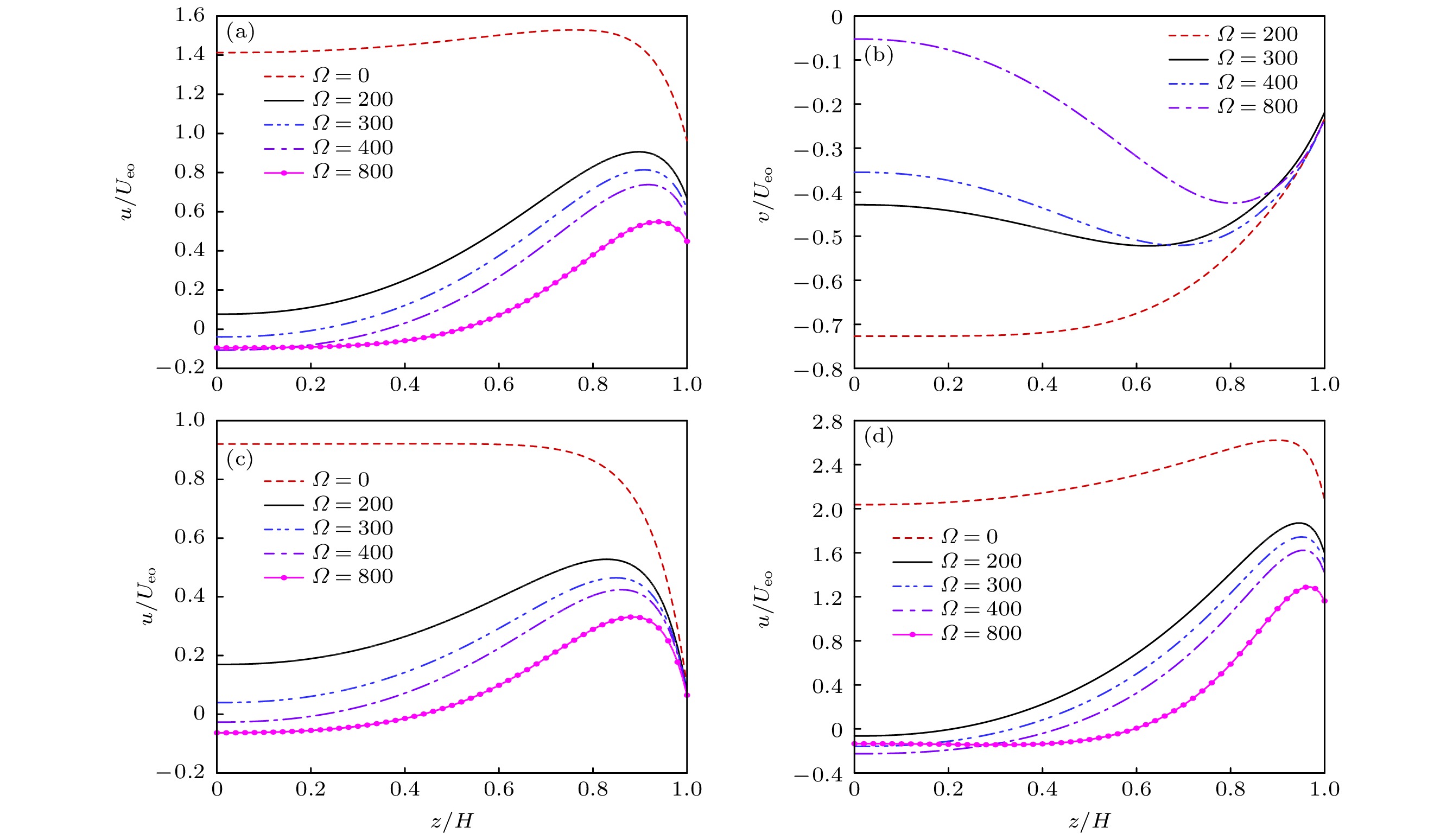
Figure 6. The influence of Hartmann number Ha on the velocity of rotating electroosmotic flow with external magnetic field, $ n = 1.2, {\text{ }}K = 10, $$ {\text{ }}\beta = 0.1, {\text{ }}\varOmega = 100{\text{ }}{\rm{rad}}/{\rm{s}}, {\text{ }}{\bar \psi _\omega } = 5{\text{ }}{\rm{V}}, {\text{ }}a = 0.05, {\text{ }}S = 1 $

DownLoad: Full-Size Img PowerPoint

图 7 旋转角速度$\varOmega $对外加磁场的旋转电渗流速度的影响, 其中$ n = 0.8, $$ {\bar \psi _\omega } = {\text{5}}\;{\rm{V}}, $$ a = 0.05, {\text{ }}Ha = 1, {\text{ }}S = 1 $ (a)$K = 10, {\text{ }}\beta = $$ 0.1;$ (b) $ K = 10, {\text{ }}\beta = 0.1; $ (c) $ K = 10, {\text{ }}\beta = 0; $ (d)$ K = 20, {\text{ }}\beta = 0.1. $

Figure 7. The influence of the rotational angular velocity $\varOmega $ on the rotational electroosmotic flow velocity of the external magnetic field, $ n = 0.8, $$ {\bar \psi _\omega } = {\text{5 }}V, $$ a = 0.05, {\text{ }}Ha = 1, {\text{ }}S = 1 $(a) $ K = 10, {\text{ }}\beta = 0.1; $ (b) $ K = 10, {\text{ }}\beta = 0.1; $ (c) $ K = 10, {\text{ }}\beta = 0; $ (d)$K = 20, $$ {\text{ }}\beta = 0.1$

DownLoad: Full-Size Img PowerPoint

图 8 旋转角速度$\varOmega $对外加磁场的旋转电渗流速度的影响, 其中$ n = 1.2, $$ {\bar \psi _\omega } = 5{\text{ }}{\rm{V}}, {\text{ }} $$ a = 0.05, {\text{ }}Ha = 1, {\text{ }}S = 1 $ (a) $\beta = 0.1, {\text{ }}K = $$ 10.$ (b) $ \beta = 0.1, {\text{ }}K = 10. $ (c) $ \beta = 0, {\text{ }}K = 10. $ (d) $\beta = 0.1, {\text{ }}K = 30$

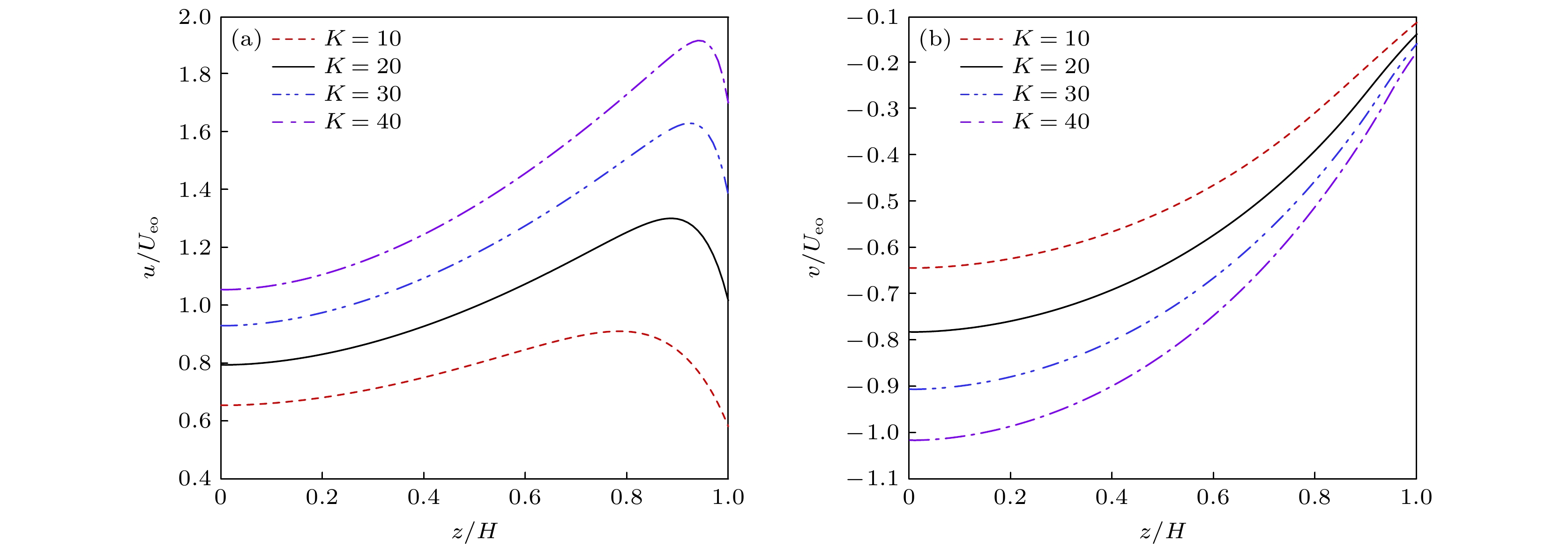
Figure 8. The influence of the rotational angular velocity $\varOmega $ on the rotational electroosmotic flow velocity of the external magnetic field, $ n = 1.2, $$ {\bar \psi _\omega } = 5{\text{ }}V, {\text{ }} $$ a = 0.05, {\text{ }}Ha = 1, {\text{ }}S = 1 $ (a) $ \beta = 0.1, {\text{ }}K = 10. $ (b) $ \beta = 0.1, {\text{ }}K = 10. $ (c) $ \beta = 0, {\text{ }}K = 10. $ (d) $\beta = 0.1, $$ {\text{ }}K = 30$

DownLoad: Full-Size Img PowerPoint

图 9 电动宽度 K 对外加磁场的旋转电渗流速度分布的影响, 其中$ n = 0.8, $ $ \beta {\text{ = 0}}{\text{.1, }}\varOmega = 100{\text{ }}{\rm{rad}}/{\rm{s}}, {\text{ }}{\bar \psi _\omega } = 5{\text{ }}{\rm{V}}, $ ${\text{ }}a = 0.05, {\text{ }}Ha = $$ 1, {\text{ }}S = $1

Figure 9. The influence of the electric width K on the velocity distribution of rotating electroosmotic flow with external magnetic field, $n = 0.8, {\text{ }}\beta {\text{ = 0}}{\text{.1, }}\varOmega = 100{\text{ rad/s}}, {\text{ }}{\bar \psi _\omega } = 5{\text{ }}V, {\text{ }}$$ a = 0.05, {\text{ }}Ha = 1, {\text{ }}S = 1 $

DownLoad: Full-Size Img PowerPoint

图 10 电动宽度 K 对外加磁场的旋转电渗流速度分布的影响, 其中$ n = 1.2, $$ \beta {\text{ = 0}}{\text{.1, }}\varOmega = 100{\text{ }}{\rm{rad}}/{\rm{s}}, {\text{ }}{\bar \psi _\omega } = 5{\text{ }}{\rm{V}}, {\text{ }}a = 0.05, {\text{ }}Ha = $$ 1, {\text{ }}S = $1

Figure 10. The influence of the electric width K on the velocity distribution of rotating electroosmotic flow with external magnetic field, $ n = 1.2, {\text{ }}\beta {\text{ = 0}}{\text{.1, }}\varOmega = 100{\text{ }}{\rm{rad}}/{\rm{s}}, {\text{ }}{\bar \psi _\omega } = 5{\text{ }}{\rm{V}}, {\text{ }} $$ a = 0.05, {\text{ }}Ha = 1, {\text{ }}S = 1 $

DownLoad: Full-Size Img PowerPoint

图 11 电动宽度 K 对外加磁场的旋转电渗流速度分布的影响, 其中$ n = 1.2, $$\beta {\text{ = 0, }}\varOmega = 100{\text{ }}{\rm{rad}}/{\rm{s}}, {\text{ }}{\bar \psi _\omega } = 5{\text{ }}{\rm{V}}, {\text{ }}a = 0.05, {\text{ }}Ha = $$ 1, {\text{ }}S =$1

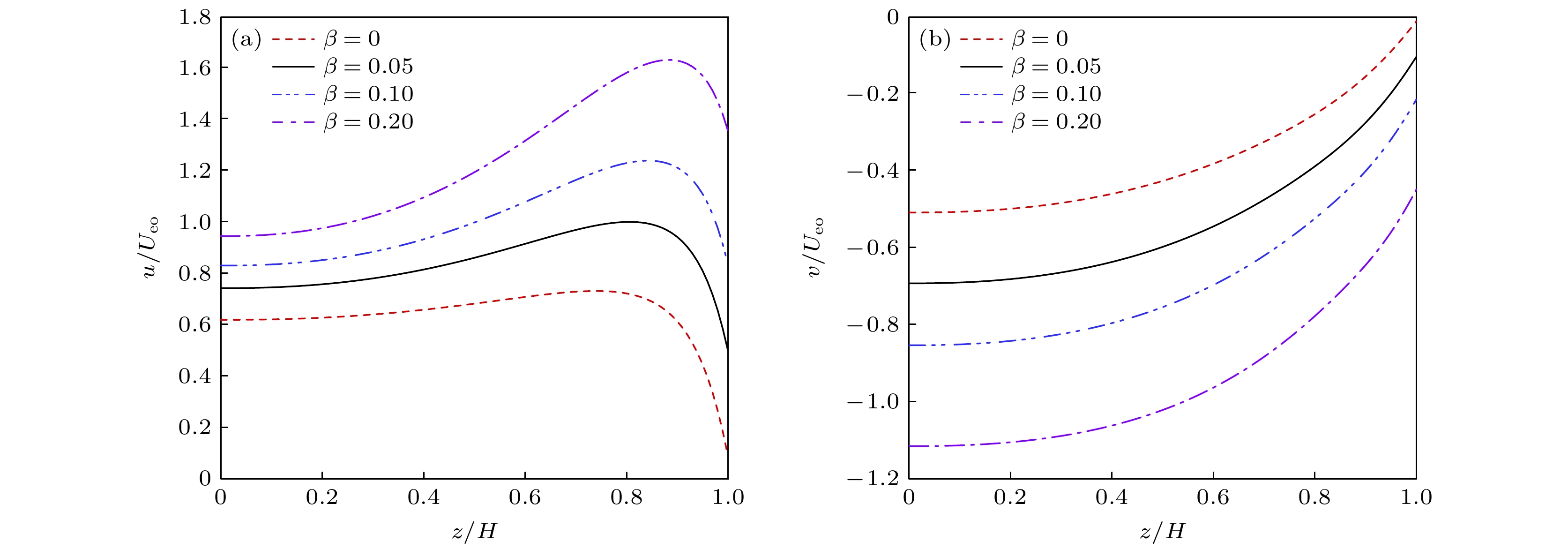
Figure 11. The influence of the electric width K on the velocity distribution of rotating electroosmotic flow with external magnetic field, $ n = 1.2, {\text{ }}\beta {\text{ = 0, }}\varOmega = 100{\text{ }}{\rm{rad}}/{\rm{s}}, {\text{ }}{\bar \psi _\omega } = 5{\text{ }}{\rm{V}}, {\text{ }} $$ a = 0.05, {\text{ }}Ha = 1, {\text{ }}S = 1 $

DownLoad: Full-Size Img PowerPoint

图 12 滑移参数$\beta $对外加磁场的旋转电渗流速度的影响, 其中$ n = 0.8, $$ K = 10, $$\varOmega = 100{\text{ }}{\rm{rad}}/{\rm{s}}, {\text{ }}{\bar \psi _\omega } = 5{\text{ }}{\rm{V}}, {\text{ }}a = 0.05, {\text{ }}Ha = $$ 1, {\text{ }}S =$1

Figure 12. The influence of the slip parameter$\beta $on the rotating electroosmotic flow velocity with an external magnetic field, $ n = 0.8, $$ K = 10, $$ \varOmega = 100{\text{ }}{\rm{rad}}/{\rm{s}}, {\text{ }}{\bar \psi _\omega } = 5{\text{ }}{\rm{V}}, {\text{ }}a = 0.05, {\text{ }}Ha = 1, {\text{ }}S = 1$

DownLoad: Full-Size Img PowerPoint

图 13 滑移参数$\beta $对外加磁场的旋转电渗流速度的影响, 其中$ n = 1.2, $$ K = 10, $$ \varOmega = 100{\text{ }}{\rm{rad}}/{\rm{s}}, {\text{ }}{\bar \psi _\omega } = 5{\text{ }}{\rm{V}}, {\text{ }}a = 0.05, {\text{ }}Ha = $$ 1, {\text{ }}S = 1 $

Figure 13. The influence of the slip parameter$\beta $on the rotating electroosmotic flow velocity with an external magnetic field, $ n = 1.2, $$ K = 10, $$\varOmega = 100{\text{ }}{\rm{rad}}/{\rm{s}}, {\text{ }}{\bar \psi _\omega } = 5{\text{ }}{\rm{V}}, {\text{ }}a = 0.05, {\text{ }}Ha = 1, {\text{ }}S = 1$

DownLoad: Full-Size Img PowerPoint

map

[1]	Stone H A, Stroock A D, Ajdari A 2004 Annu. Rev. Fluid Mech. 36 381 Google Scholar
[2]	Patel M, Kruthiventi S S H, Kaushik P 2020 Colloids Surf. B 193 111058 Google Scholar
[3]	Srinivas, Bhadri 2016 Colloids Surf. A 492 144 Google Scholar
[4]	Nekoubin N 2018 J. Non-Newtonian Fluid Mech. 260 54 Google Scholar
[5]	Baños R D, Arcos J C, Bautista O, Méndez F, Merchán-Cruz E A 2021 J. Braz. Soc. Mech. Sci. 43 1 Google Scholar
[6]	Baños R, Arcos J, Bautista O, Méndez F 2020 Defect Diffus. Forum 399 92 Google Scholar
[7]	姜玉婷, 齐海涛 2015 64 174702 Google Scholar Jiang Y T, Qi H T 2015 Acta Phys. Sin. 64 174702 Google Scholar
[8]	Ajdari A 2002 Phys. Rev. E 65 16301 Google Scholar
[9]	Chang C C, Wang C Y 2011 Phys. Rev. E 84 056320 Google Scholar
[10]	Song J, Wang S W, Zhao M L, Li N 2020 Z. Naturforsch. A: Phys. Sci. 75 649 Google Scholar
[11]	Shit G C, Mondal A, Sinha A, Kundu P K 2016 Colloids Surf. A 489 249 Google Scholar
[12]	刘全生, 杨联贵, 苏洁 2013 62 144702 Google Scholar Liu Q S, Yang L G, Su J 2013 Acta Phys. Sin. 62 144702 Google Scholar
[13]	段娟, 陈耀钦, 朱庆勇 2016 65 034702 Google Scholar Duan J, Chen Y Q, Zhu Q Y 2016 Acta Phys. Sin. 65 034702 Google Scholar
[14]	Weston M C, Gerner M D, Fritsch I 2010 Anal. Chem. 82 3411 Google Scholar
[15]	Jian Y J, Chang L 2015 AIP Adv. 5 057121 Google Scholar
[16]	Xie Z Y, Jian Y J 2017 Colloids Surf. A 529 334 Google Scholar
[17]	Habib U, Hayat T, Ahmad S, Alhodaly M S 2021 Int. Commun. Heat Mass Transfer 122 105111 Google Scholar
[18]	Sarkar S, Ganguly S 2017 J. Non-Newtonian Fluid Mech. 250 18 Google Scholar
[19]	Yang C H, Jian Y J, Xie Z Y, Li F Q 2020 Micromachines 11 418 Google Scholar
[20]	Xie Z Y, Jian Y J 2017 Energy 139 1080 Google Scholar
[21]	Wang S W, Li N, Zhao M L, Azese M N 2018 Z. Naturforsch. A: Phys. Sci. 73 825 Google Scholar
[22]	Xie Z Y, Jian Y J 2014 Colloids Surf. A 461 231 Google Scholar
[23]	Bird R B, Armstrong R C, Hassager O, Curtiss C F, Middleman S 1978 Phys. Today 31 54 Google Scholar

[1]	Mu Jiang-Yong, Cui Ji-Feng, Chen Xiao-Gang, Zhao Yi-Kang, Tian Yi-Lin, Yu Xin-Ru, Yuan Man-Yu. Electroosmotic flow and heat transfer characteristics of a class of biofluids in microchannels at high Zeta potential. Acta Physica Sinica, 2024, 73(6): 064701. doi: 10.7498/aps.73.20231685
[2]	Yu Xin-Ru, Cui Ji-Feng, Chen Xiao-Gang, Mu Jiang-Yong, Qiao Yu-Ran. Time period electroosmotic flow of a class of incompressible micropolar fluid in parallel plate microchannels under high Zeta potential. Acta Physica Sinica, 2024, 73(16): 164701. doi: 10.7498/aps.73.20240591
[3]	Xu Ming, Xu Li-Qing, Zhao Hai-Lin, Li Ying-Ying, Zhong Guo-Qiang, Hao Bao-Long, Ma Rui-Rui, Chen Wei, Liu Hai-Qing, Xu Guo-Sheng, Hu Jian-Sheng, Wan Bao-Nian, the EAST Team. Summary of magnetohydrodynamic instabilities and internal transport barriers under condition of q_min$\approx $2 in EAST tokamak. Acta Physica Sinica, 2023, 72(21): 215204. doi: 10.7498/aps.72.20230721
[4]	Gao Xiao-Wei, Ding Jin-Xing, Liu Hua-Yu. Finite line method and its application in coupled heat transfer between fluid-solid domains. Acta Physica Sinica, 2022, 71(19): 190201. doi: 10.7498/aps.71.20220833
[5]	He Yu-Bo, Tang Xian-Hua, Lin Xiao-Yan. Numerical simulation of a class of FitzHugh-Nagumo systems based on the lattice Boltzmann method. Acta Physica Sinica, 2016, 65(15): 154701. doi: 10.7498/aps.65.154701
[6]	Liu Quan, Yu Ming, Lin Zhong, Wang Rui-Li. Conservative sliding algorithms for hydrodynamics. Acta Physica Sinica, 2015, 64(19): 194701. doi: 10.7498/aps.64.194701
[7]	Zhu Xiao-Min, Ren Xin-Cheng, Guo Li-Xin. Study on wide-band scattering from rectangular cross-section above rough land surface with exponential type distribution using FDTD. Acta Physica Sinica, 2014, 63(5): 054101. doi: 10.7498/aps.63.054101
[8]	Liu Jian-Xiao, Zhang Jun-Liang, Su Ming-Min. Finite-difference time domain method for the analysis of radar scattering characteristic of metal target coated with anisotropic ferrite. Acta Physica Sinica, 2014, 63(13): 137501. doi: 10.7498/aps.63.137501
[9]	Wang Guang-Hui, Wang Lin-Xue, Wang Deng-Shan, Liu Cong-Bo, Shi Yu-Ren. Numerical investigation on the interaction between multi-Compacton of K(m,n,p) equation. Acta Physica Sinica, 2014, 63(18): 180206. doi: 10.7498/aps.63.180206
[10]	Yang Li-Xia, Ma Hui, Shi Wei-Dong, Shi Li-Juan, Yu Ping-Ping. Finite difference time domain analysis on electromagnetic scattering characteristic of plasma thin layer based on surface impedance boundary condition method. Acta Physica Sinica, 2013, 62(3): 034102. doi: 10.7498/aps.62.034102
[11]	Peng Wu, He Yi-Gang, Fang Ge-Feng, Fan Xiao-Teng. An ameliorative algorithm of two-dimensional Poisson equation based on genetic parallel successive over-relaxation method. Acta Physica Sinica, 2013, 62(2): 020301. doi: 10.7498/aps.62.020301
[12]	Zhuansun Xu, Ma Xi-Kui. An absorbing boundary condition for general dispersive medium and general FDTD spatial scheme. Acta Physica Sinica, 2012, 61(11): 110206. doi: 10.7498/aps.61.110206
[13]	Chang Long, Jian Yong-Jun. Time periodic electroosmotic flow of the generalized Maxwell fluids between two micro-parallel plates with high Zeta potential. Acta Physica Sinica, 2012, 61(12): 124702. doi: 10.7498/aps.61.124702
[14]	Ren Xin-Cheng, Guo Li-Xin, Jiao Yong-Chang. Investigation of electromagnetic scattering interaction between the column with rectangular cross-section and rough land surface covered with snow using finite difference time domain method. Acta Physica Sinica, 2012, 61(14): 144101. doi: 10.7498/aps.61.144101
[15]	Yin Jing-Chan, Xiao Xiao-Sheng, Yang Chang-Xi. Dynamics of relaxation oscillation caused by stimulated Brillouin scattering in optical fiber and its suppression. Acta Physica Sinica, 2009, 58(12): 8316-8325. doi: 10.7498/aps.58.8316
[16]	. A recursive convolution-finite-difference time-domain implementation of electromagnetic scattering by magnetized ferrite medium. Acta Physica Sinica, 2007, 56(12): 6937-6944. doi: 10.7498/aps.56.6937
[17]	Cang Yu, Lu Xin, Wu Hui-Chun, Zhang Jie. Effects of ponderomotive forces and space-charge field on laser plasma hydrodynamics. Acta Physica Sinica, 2005, 54(2): 812-817. doi: 10.7498/aps.54.812
[18]	Tan Xin-Yu, Zhang Duan-Ming, Li Zhi-Hua, Guan Li, Li Li. Target ablation characteristics of thin films during nanosecond pulsed laser deposition in the ablation process. Acta Physica Sinica, 2005, 54(8): 3915-3921. doi: 10.7498/aps.54.3915
[19]	Zhao Hong-Dong, Song Dian-You, Zhang Zhi-Feng, Sun Ji ng, Sun Mei, Wu Yi, Wen Xing-Rao. Influence of the potential in n-type DBR on threshold in vertical-cavity surface-emitting lasers. Acta Physica Sinica, 2004, 53(11): 3744-3747. doi: 10.7498/aps.53.3744
[20]	Liang Hong-Chang, Zhu Qing-Xin. . Acta Physica Sinica, 2002, 51(10): 2202-2204. doi: 10.7498/aps.51.2202

Catalog

Vol. 71, Issue 13 - 2022-07-05

Metrics

Abstract views: 4037
PDF Downloads: 54
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板