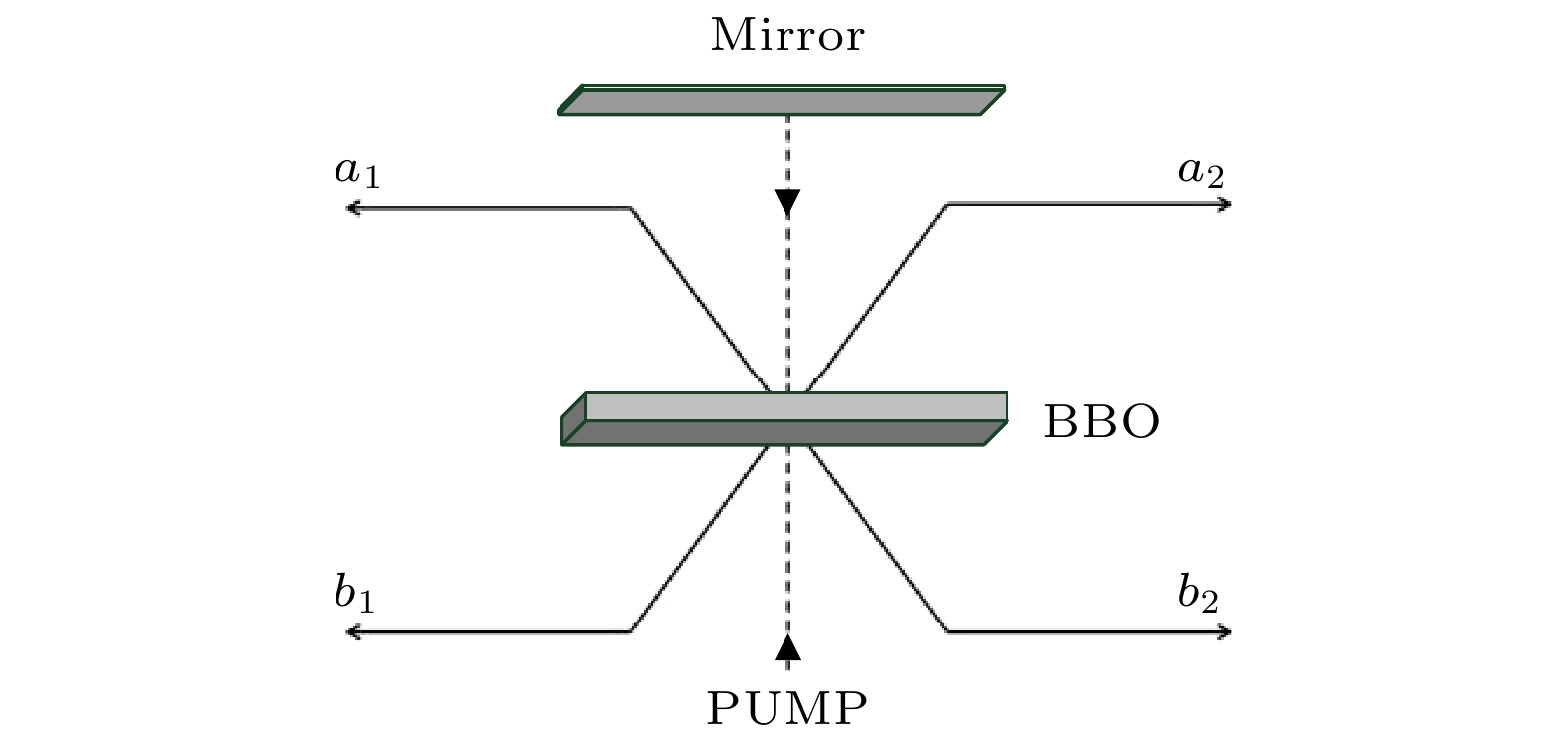
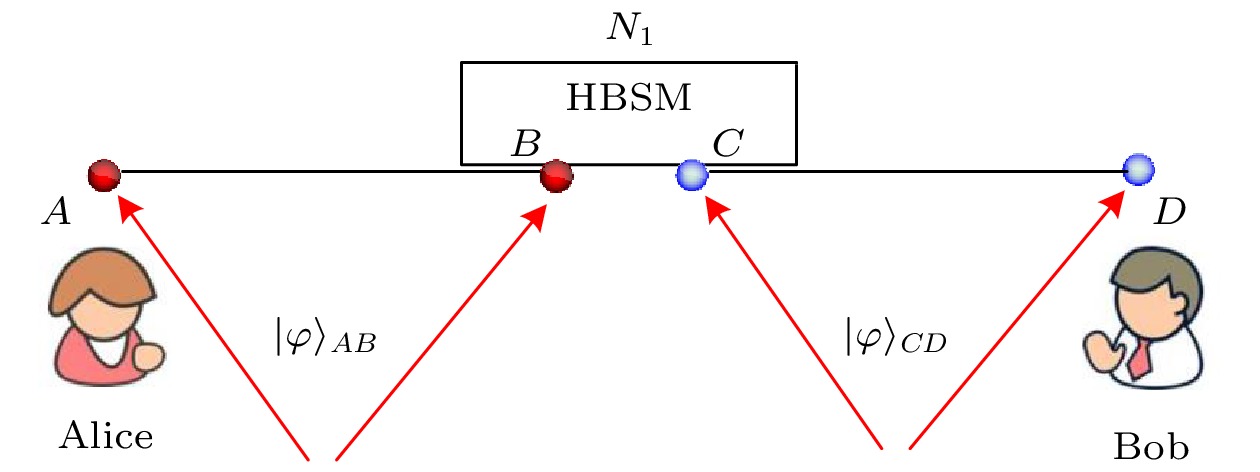
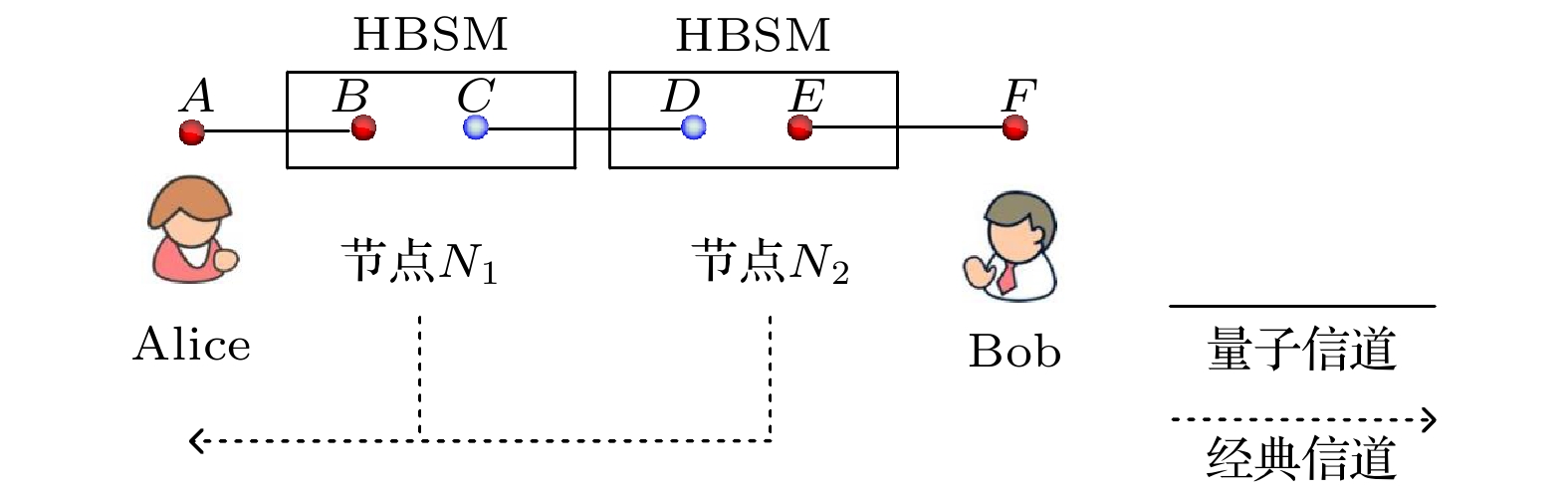
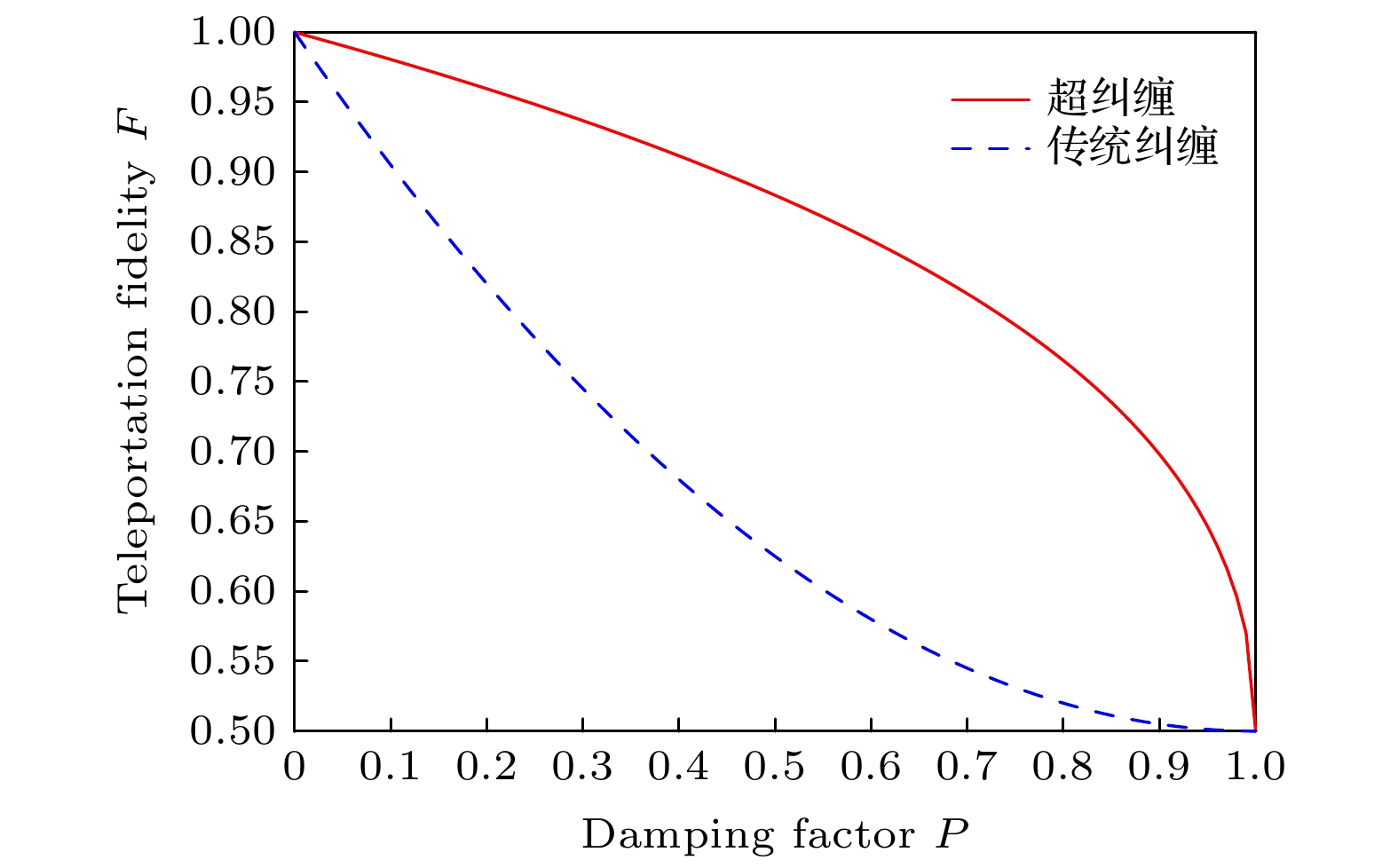
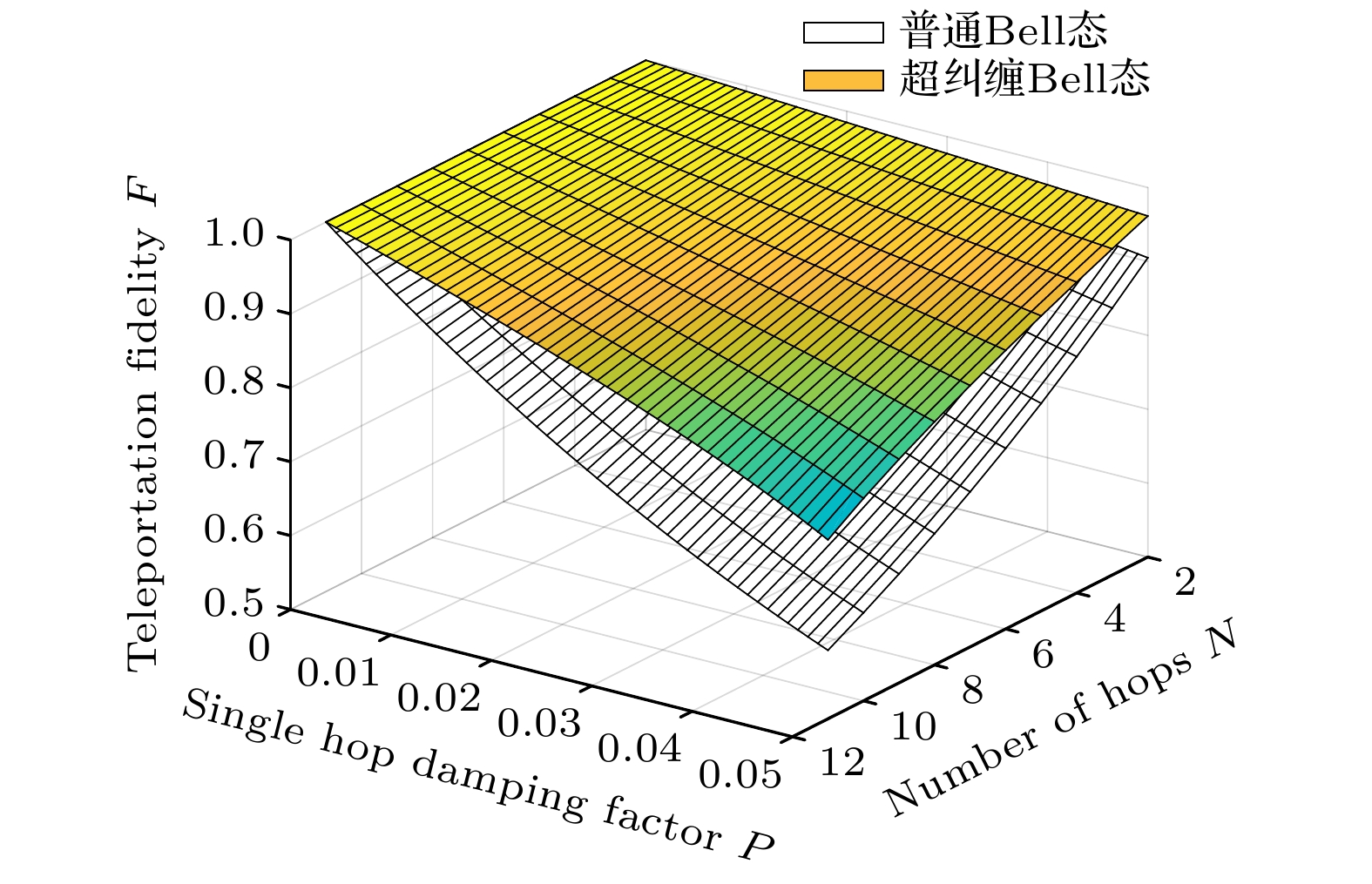
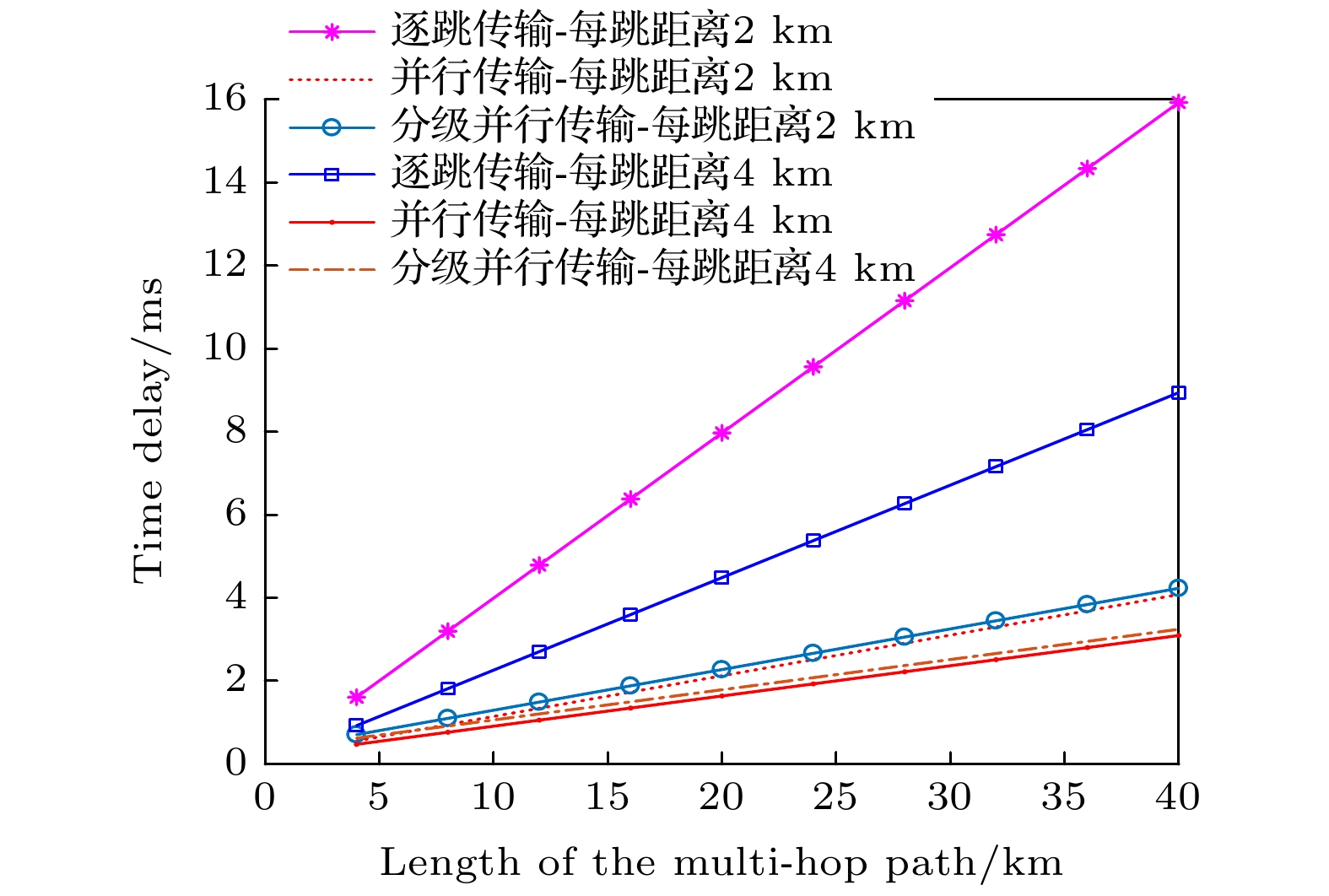
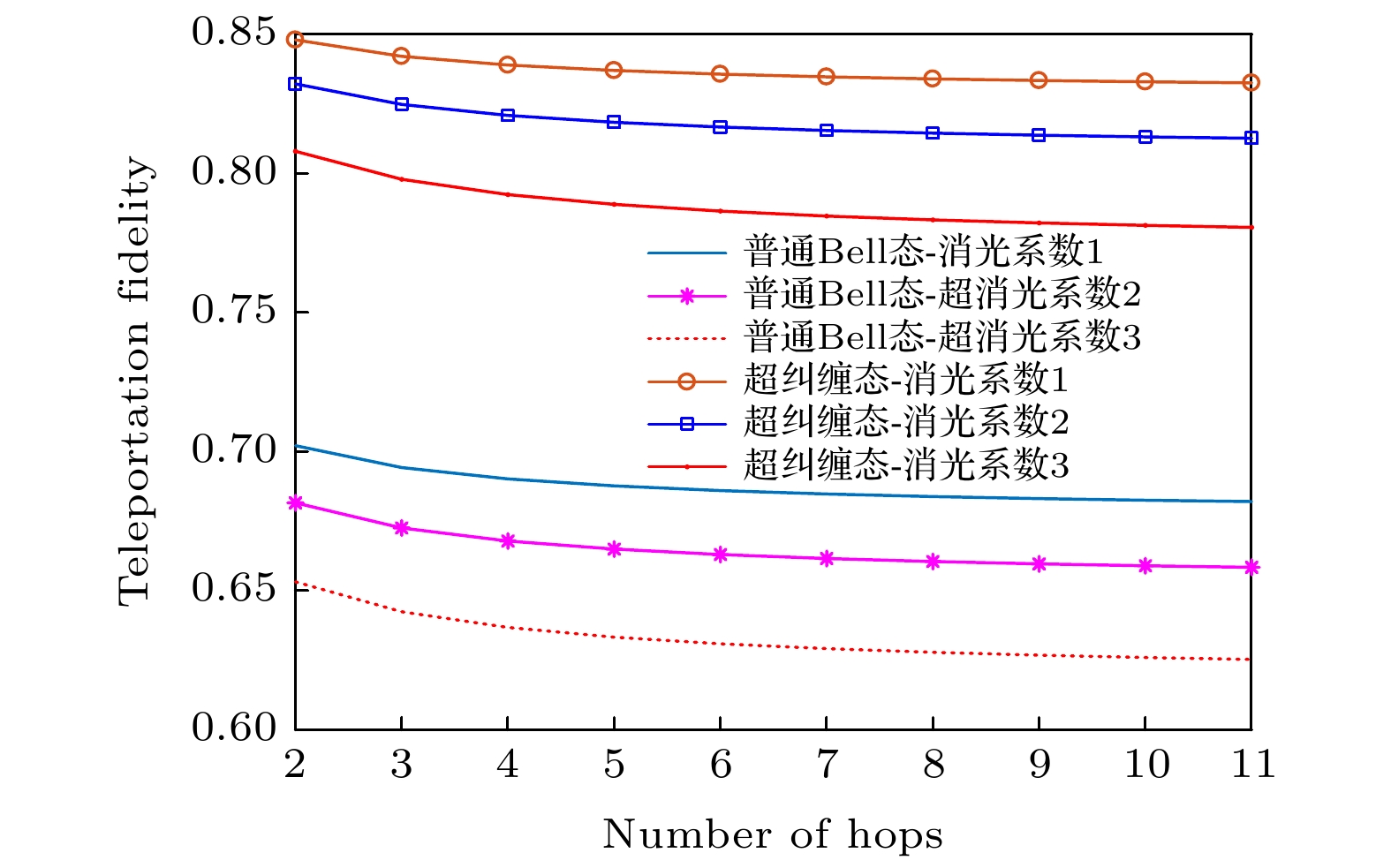
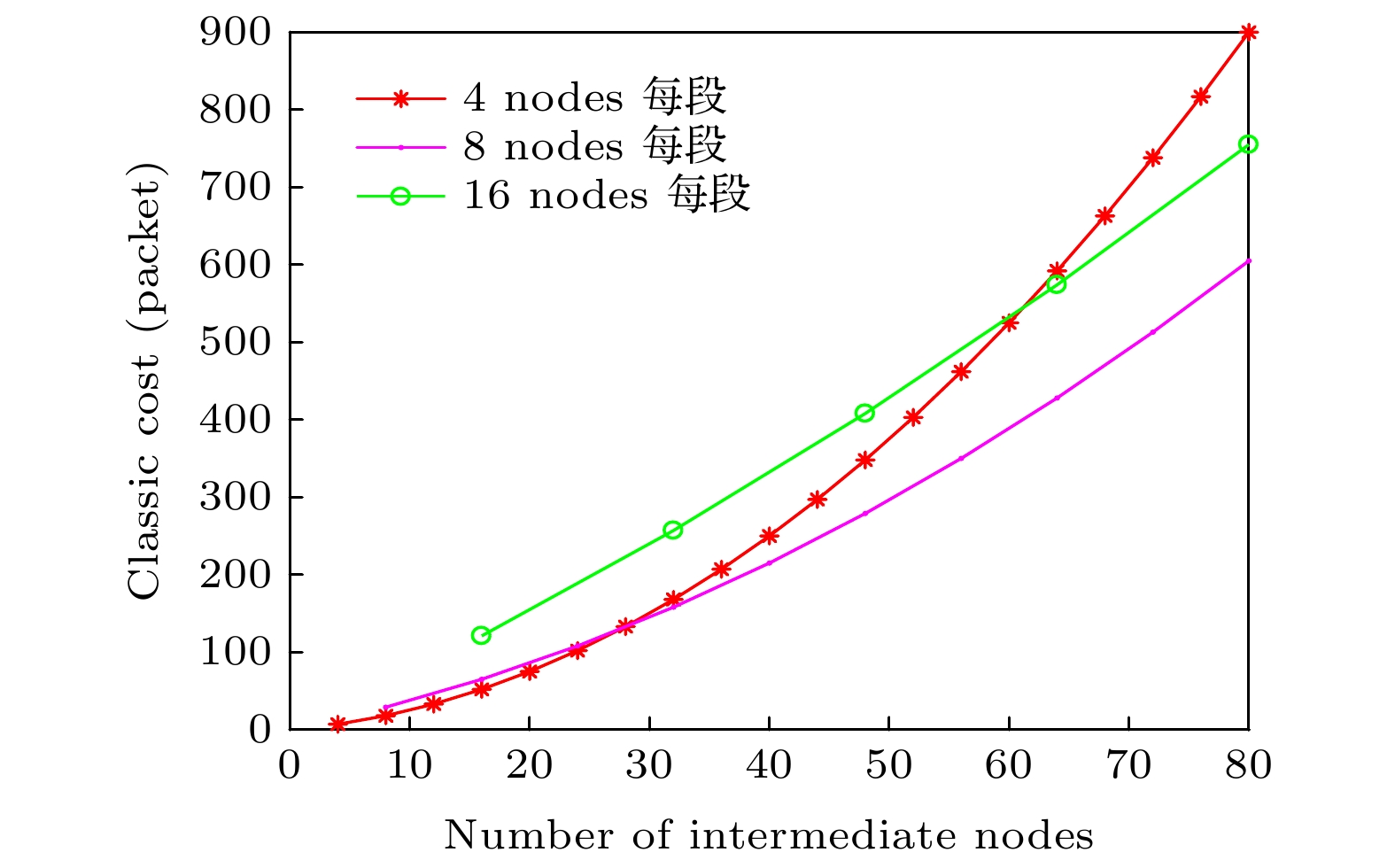
-
Entanglement swapping (ES) based multi-hop quantum information transmission is a fundamental way to realize long-distance quantum communication. However, in the conventional quantum networks, the entanglement in one degree of freedom (DOF) of photon system is usually used as a quantum channel, showing disadvantages of low capacity and susceptibility to noise. In this paper, we present an efficient multi-hop quantum hyperentanglement swapping (HES) method based on hyperentanglement, which utilizes the entangled photos in polarization and spatial-mode DOFs to establish the hyperentangled multi-hop quantum channel. Taking long-distance hyperentanglement based quantum teleportation for example, we first describe a basic hop by hop HES scheme. Then, in order to reduce the end-to-end delay of this scheme, we propose a simultaneous HES (SHES) scheme, in which the intermediate quantum nodes perform hyperentangled Bell state measurements concurrently. On the basis of this scheme, we further put forward a hierarchical SHES (HSHES) scheme that can reduce the classical information cost. Theoretical analysis and simulation results show that the end-to-end delay of HSHES is similar to that of SHES, meanwhile, the classical information cost of HSHES is much lower than that of SHES, showing a better tradeoff between the two performance metrics. Compared with the traditional ES methods, the scheme proposed in this paper is conductive to meeting the requirements for long-distance hyperentanglement based quantum communication, which has positive significance for building more efficient quantum networks in the future.
[1] Pan J W, Chen Z B, Lu Y C, Weinfurter H, Zeilinger A, Zukowsk M 2012 Rev. Mod. Phys. 84 777
Google Scholar
[2] Bennett C H, Brassard G, Crépeau C, Jozsa R, Peres A, Wootters W K 1993 Phys. Rev. Lett. 70 1895
Google Scholar
[3] 范桁 2018 67 120301
Google Scholar
Fan H 2018 Acta Phys. Sin. 67 120301
Google Scholar
[4] Luo Y H, Zhong H S, Erhard M, Wang X L, Peng C L, Krenn M, Jiang X, Li L, Liu N L, Lu C Y, Zeilinger A, Pan J W 2019 Phys. Rev. Lett. 123 070505
Google Scholar
[5] Hassanpour S, Houshmand M 2016 Quantum Inf. Process 15 905
Google Scholar
[6] Zang P, Song R, Jiang Y 2017 Chinese Journal of Quantum Electronics 34 456
[7] Paulson K G, Panigrahi P K 2019 Phys. Rev. A 100 052325
Google Scholar
[8] Shor P W, Preskill J 2000 Phys. Rev. Lett. 85 441
Google Scholar
[9] Lo H K, Curty M, Qi B 2012 Phys. Rev. Lett. 108 130503
Google Scholar
[10] Gisin N, Ribordy G, Tittel W, Zbinden H 2002 Rev. Mod. Phys. 74 145
Google Scholar
[11] Long G L, Liu X S 2002 Phys. Rev. A 65 032302
Google Scholar
[12] 曹正文, 赵光, 张爽浩, 冯晓毅, 彭进业 2016 65 230301
Google Scholar
Cao Z W, Zhao G, Zhang S H, Feng X Y, Peng J Y 2016 Acta Phys. Sin. 65 230301
Google Scholar
[13] Chen J P, Zhang C, Liu Y, Jiang C, Zhang W J, Hu X L, Guan J Y, Yu Z W, Xu H, Lin J, Li M J, Chen H, Li H, You, L X, Wang Z, Wang X B, Zhang Q, Pan J W 2020 Phys. Rev. Lett. 124 070501
Google Scholar
[14] 龙桂鲁, 潘栋 2021 信息通信技术与政策 7 7
Google Scholar
Long G L, Pan D 2021 Telecommunications Network Technology 7 7
Google Scholar
[15] Sheng Y B, Guo F G, Long G L 2010 Phys Rev. A 82 032318
Google Scholar
[16] Hong C H, Heo J, Lim J I, Yang H J 2014 Chin. Phys. B 23 090309
Google Scholar
[17] Wang X L, Cai X D, Su Z E, Cheng M C, Wu D, Li L, Liu N L, Lu C Y, Pan J W 2015 Nature 518 516
Google Scholar
[18] Xu L 2020 Modern Phys Lett. B 34 2050353
Google Scholar
[19] 彭承志, 潘建伟 2016 中国科学院院刊 31 1096
Peng C Z, Pan J W 2016 Bulletin of Chinese Academy of Sciences 31 1096
[20] Liao S K, Cai W Q 2018 Phys. Rev. Lett. 120 030501
Google Scholar
[21] 赖俊森, 赵文玉, 张海懿 2021 信息通信技术与政策 7 6
Google Scholar
Lai J S, Zhao W Y, Zhang H Y 2021 Telecommunications Network Technology 7 6
Google Scholar
[22] 聂敏, 张帆, 杨光, 张美玲, 孙爱晶, 裴昌幸 2021 70 040303
Google Scholar
Nie M, Zhang F, Yang G, Zhang M L, Sun A J, Pei C X 2021 Acta Phys. Sin. 70 040303
Google Scholar
[23] 杨光, 廉保旺, 聂敏 2015 64 010303
Google Scholar
Yang G, Lian B W, Nie M 2015 Acta Phys. Sin. 64 010303
Google Scholar
[24] 杨光, 廉保旺, 聂敏 2015 64 240304
Google Scholar
Yang G, Lian B W, Nie M 2015 Acta Phys. Sin. 64 240304
Google Scholar
[25] Briegel H J, Raussendorf R 2001 Phys. Rev. Lett. 86 910
Google Scholar
[26] Pan J W, Bouwmeester D, Weinfurter H, Zeilinger A 1998 Phys. Rev. Lett. 80 3891
Google Scholar
[27] Dotsenko I S, Korobka R 2018 Commun. Theor. Phys. 69 143
Google Scholar
[28] Li Y H, Li X L, Nie L P, Sang M H 2016 Int. J. Theor. Phys. 55 1820
Google Scholar
[29] Tao Y X, Xu J, Zhang Z C 2013 Chin. Phys. B 22 090311
Google Scholar
[30] Espoukeh P, Pedram P 2014 Int. J. Theor. Phys. 13 1789
[31] Du Z L, Li X L, Liu X J 2020 Int. J. Theor. Phys. 59 622
Google Scholar
[32] Gao X Q, Zhang Z C, Gong Y X, Sheng B, Yu X T 2017 J. Opt. Soc. Am. B-Opt. Phys. 34 142
Google Scholar
[33] Cai X F, Yu X T, Shi L H, Zhang Z C 2014 Front. Phys. 9 646
Google Scholar
[34] Xiong P Y, Yu X T, Zhang Z C, Zhan H T, Hua J Y 2017 Front. Phys. 12 1
[35] Wang K, Yu X T, Lu S L, Gong X Y 2014 Phys Rev. A 89 022329
Google Scholar
[36] Tao Y, Zhang Q, Zhang J, Yin J, Zhao Z, Zukowski M, Chen Z B, Pan J W 2005 Phys. Rev. Lett. 95 240406
Google Scholar
[37] 郭肖 2020 硕士学位论文 (西安: 西安电子科技大学 )
Guo X 2020 M. S. Dissertation (Shannxi: Xidian University) (in Chinese)
[38] 聂敏, 王超旭, 杨光, 张美玲, 孙爱晶, 裴昌幸 2021 70 030301
Google Scholar
Nie M, Wang C X, Yang G, Sun A J, Pei C X 2021 Acta Phys. Sin. 70 030301
Google Scholar
[39] 张秀再, 徐茜, 刘邦宇 2020 光学学报 40 0327001
Google Scholar
Zhang X Z, Xu Q, Liu B Y 2020 Acta Optica Sinica 40 0327001
Google Scholar
[40] Xu J, Chen X G, Xiao H W, Wang P X, Ma M 2021 Appl. Sci. 11 10869
Google Scholar
[41] Cabello A 2000 Phys. Rev. Lett. 85 5635
Google Scholar
-
图 1 极化和空间模自由度中超纠缠态产生原理
Figure 1. Schematic diagram of the setup to generate hyperentanglement in both polarization and spatial-mode DOFs.
图 2 超纠缠交换原理
Figure 2. Schematic diagram of hyperentanglement swapping.
图 3 并行超纠缠交换
Figure 3. Schematic diagram of simultaneous hyperentanglement swapping.
图 4 多级并行纠缠交换原理
Figure 4. Schematic diagram of hierarchical simultaneous entanglement swapping.
图 5 隐形传态保真度
Figure 5. Teleportation fidelity.
图 6 隐形传态保真度随跳数及幅值阻尼系数的变化
Figure 6. Teleportation fidelity versus the number of hops and the damping factor.
图 7 端到端纠缠建立时延随中间节点个数的关系
Figure 7. Time delay versus the number of intermediate nodes.
图 8 单跳距离与端到端时延的关系
Figure 8. End to end time delay versus the per-hop length.
图 9 跳数选择与隐形传态保真度的关系
Figure 9. Teleportation fidelity versus the choice of the number of hops.
图 10 中间节点数与经典信息开销关系
Figure 10. Classical costs versus the number of intermediate nodes.
图 11 每段节点数与经典信息开销的关系
Figure 11. Classical costs versus number of intermediate nodes in one segment.
图 12 跳数与纠缠交换效率的关系
Figure 12. Entanglement swapping efficiency versus the number of hops.
表 1 幺正变换表
Table 1. Unitary operations.
B和C的量子态 编码结果 A和D的量子态 Bob的幺正变换 $ \left| {{\phi ^{\text{ + }}}} \right\rangle _{P} \left| {{\phi ^{\text{ + }}}} \right\rangle _{S} $ 0000 $ \left| {{\phi ^{\text{ + }}}} \right\rangle _{P} \left| {{\phi ^{\text{ + }}}} \right\rangle _{S} $ $ {U_1} = \sigma _I^P \otimes \sigma _I^S $ $ \left| {{\phi ^{\text{ + }}}} \right\rangle _{P} \left| {{\phi ^ - }} \right\rangle _{S} $ 0001 $ \left| {{\phi ^{\text{ + }}}} \right\rangle _{P} \left| {{\phi ^ - }} \right\rangle _{S} $ $ {U_2} = \sigma _I^P \otimes \sigma _Z^S $ $ \left| {{\phi ^ - }} \right\rangle _{P} \left| {{\phi ^ + }} \right\rangle _{S} $ 0010 $ \left| {{\phi ^ - }} \right\rangle _{P} \left| {{\phi ^ + }} \right\rangle _{S} $ $ {U_3} = \sigma _Z^P \otimes \sigma _I^S $ $ \left| {{\phi ^ - }} \right\rangle _{P} \left| {{\phi ^ - }} \right\rangle _{S} $ 0011 $ \left| {{\phi ^ - }} \right\rangle _{P} \left| {{\phi ^ - }} \right\rangle _{S} $ $ {U_4} = \sigma _Z^P \otimes \sigma _Z^S $ $ \left| {{\psi ^{\text{ + }}}} \right\rangle _{P} \left| {{\phi ^{\text{ + }}}} \right\rangle _{S} $ 0100 $ \left| {{\psi ^{\text{ + }}}} \right\rangle _{P} \left| {{\phi ^{\text{ + }}}} \right\rangle _{S} $ $ {U_5} = \sigma _X^P \otimes \sigma _I^S $ $ \left| {{\psi ^{\text{ + }}}} \right\rangle _{P} \left| {{\phi ^ - }} \right\rangle _{S} $ 0101 $ \left| {{\psi ^{\text{ + }}}} \right\rangle _{P} \left| {{\phi ^ - }} \right\rangle _{S} $ $ {U_6} = \sigma _X^P \otimes \sigma _Z^S $ $ \left| {{\psi ^ - }} \right\rangle _{P} \left| {{\phi ^ + }} \right\rangle _{S} $ 0110 $ \left| {{\psi ^ - }} \right\rangle _{P} \left| {{\phi ^ + }} \right\rangle _{S} $ ${U_7} = - {{i}}\sigma _Y^P \otimes \sigma _I^S$ $ \left| {{\psi ^ - }} \right\rangle _{P} \left| {{\phi ^ - }} \right\rangle _{S} $ 0111 $ \left| {{\psi ^ - }} \right\rangle _{P} \left| {{\phi ^ - }} \right\rangle _{S} $ ${U_8} = - {{i}}\sigma _Y^P \otimes \sigma _Z^S$ $ \left| {{\phi ^{\text{ + }}}} \right\rangle _{p} \left| {{\psi ^{\text{ + }}}} \right\rangle _{S} $ 1000 $ \left| {{\phi ^{\text{ + }}}} \right\rangle _{p} \left| {{\psi ^{\text{ + }}}} \right\rangle _{S} $ $ {U_9} = \sigma _I^P \otimes \sigma _X^S $ $ \left| {{\phi ^{\text{ + }}}} \right\rangle _{p} \left| {{\psi ^ - }} \right\rangle _{S} $ 1001 $ \left| {{\phi ^{\text{ + }}}} \right\rangle _{p} \left| {{\psi ^ - }} \right\rangle _{S} $ ${U_{10} } = \sigma _I^P \otimes - {{i}}\sigma _Y^S$ $ \left| {{\phi ^ - }} \right\rangle _{p} \left| {{\psi ^ + }} \right\rangle _{S} $ 1010 $ \left| {{\phi ^ - }} \right\rangle _{p} \left| {{\psi ^ + }} \right\rangle _{S} $ $ {U_{11}} = \sigma _Z^P \otimes \sigma _X^S $ $ \left| {{\phi ^ - }} \right\rangle _{p} \left| {{\psi ^ - }} \right\rangle _{S} $ 1011 $ \left| {{\phi ^ - }} \right\rangle _{p} \left| {{\psi ^ - }} \right\rangle _{S} $ ${U_{12} } = \sigma _Z^P \otimes - {{i}}\sigma _Y^S$ $ \left| {{\psi ^ + }} \right\rangle _{P} \left| {{\psi ^ + }} \right\rangle _{S} $ 1100 $ \left| {{\psi ^ + }} \right\rangle _{P} \left| {{\psi ^ + }} \right\rangle _{S} $ $ {U_{13}} = \sigma _X^P \otimes \sigma _X^S $ $ \left| {{\psi ^ + }} \right\rangle _{P} \left| {{\psi ^ - }} \right\rangle _{S} $ 1101 $ \left| {{\psi ^ + }} \right\rangle _{P} \left| {{\psi ^ - }} \right\rangle _{S} $ ${U_{14} } = \sigma _X^P \otimes - {{i}}\sigma _Y^S$ $ \left| {{\psi ^ - }} \right\rangle _{P} \left| {{\psi ^ + }} \right\rangle _{S} $ 1110 $ \left| {{\psi ^ - }} \right\rangle _{P} \left| {{\psi ^ + }} \right\rangle _{S} $ ${U_{15} } = - {{i}}\sigma _Y^P \otimes \sigma _X^S$ $ \left| {{\psi ^ - }} \right\rangle _{P} \left| {{\psi ^ - }} \right\rangle _{S} $ 1111 $ \left| {{\psi ^ - }} \right\rangle _{P} \left| {{\psi ^ - }} \right\rangle _{S} $ ${U_{16} } = - {{i}}\sigma _Y^P \otimes - {\rm{i} }\sigma _Y^S$ 
DownLoad: CSV
表 2 多跳并行幺正变换表
Table 2. Multi-hop parallel entanglement swapping unitary operations
N1, N2, ···NN – 1 测量结果 Alice的幺正变换 $ \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1}} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2}} \otimes \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1}} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2}} = 1 $ $ {U_1} = \sigma _I^P \otimes \sigma _I^S $ $ \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1}} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2}} \otimes \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1}} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2} = 1 $ $ {U_2} = \sigma _I^P \otimes \sigma _Z^S $ $ \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1}} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2}} \otimes \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2}} = 1 $ $ {U_3} = \sigma _I^P \otimes \sigma _X^S $ $ \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1}} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2}} \otimes \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2} = 1 $ $ {U_4} = \sigma _I^P \otimes - i\sigma _Y^S $ $ \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1}} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2} \otimes \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1}} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2}} = 1 $ $ {U_5} = \sigma _I^P \otimes \sigma _I^S $ $ \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1}} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2} \otimes \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1}} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2} = 1 $ $ {U_6} = \sigma _Z^P \otimes \sigma _Z^S $ $ \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1}} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2} \otimes \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2}} = 1 $ $ {U_7} = \sigma _Z^P \otimes \sigma _X^S $ $ \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1}} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2} \otimes \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2} = 1 $ $ {U_8} = \sigma _Z^P \otimes - i\sigma _Y^S $ $ \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2}} \otimes \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1}} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2}} = 1 $ $ {U_9} = \sigma _X^P \otimes \sigma _I^S $ $ \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2}} \otimes \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1}} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2} = 1 $ $ {U_{10}} = \sigma _X^P \otimes \sigma _Z^S $ $ \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2}} \otimes \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2}} = 1 $ $ {U_{11}} = \sigma _X^P \otimes \sigma _X^S $ $ \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2}} \otimes \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2} = 1 $ $ {U_{12}} = \sigma _X^P \otimes - i\sigma _Y^S $ $ \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2} \otimes \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1}} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2}} = 1 $ $ {U_{13}} = - i\sigma _Y^P \otimes \sigma _I^S $ $ \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2} \otimes \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1}} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2} = 1 $ $ {U_{14}} = - i\sigma _Y^P \otimes \sigma _Z^S $ $ \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2} \otimes \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2}} = 1 $ $ {U_{15}} = - i\sigma _Y^P \otimes \sigma _X^S $ $ \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2} \otimes \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2} = 1 $ $ {U_{1{\text{6}}}} = - i\sigma _Y^P \otimes - i\sigma _Y^S $
DownLoad: CSV
-
[1] Pan J W, Chen Z B, Lu Y C, Weinfurter H, Zeilinger A, Zukowsk M 2012 Rev. Mod. Phys. 84 777
Google Scholar
[2] Bennett C H, Brassard G, Crépeau C, Jozsa R, Peres A, Wootters W K 1993 Phys. Rev. Lett. 70 1895
Google Scholar
[3] 范桁 2018 67 120301
Google Scholar
Fan H 2018 Acta Phys. Sin. 67 120301
Google Scholar
[4] Luo Y H, Zhong H S, Erhard M, Wang X L, Peng C L, Krenn M, Jiang X, Li L, Liu N L, Lu C Y, Zeilinger A, Pan J W 2019 Phys. Rev. Lett. 123 070505
Google Scholar
[5] Hassanpour S, Houshmand M 2016 Quantum Inf. Process 15 905
Google Scholar
[6] Zang P, Song R, Jiang Y 2017 Chinese Journal of Quantum Electronics 34 456
[7] Paulson K G, Panigrahi P K 2019 Phys. Rev. A 100 052325
Google Scholar
[8] Shor P W, Preskill J 2000 Phys. Rev. Lett. 85 441
Google Scholar
[9] Lo H K, Curty M, Qi B 2012 Phys. Rev. Lett. 108 130503
Google Scholar
[10] Gisin N, Ribordy G, Tittel W, Zbinden H 2002 Rev. Mod. Phys. 74 145
Google Scholar
[11] Long G L, Liu X S 2002 Phys. Rev. A 65 032302
Google Scholar
[12] 曹正文, 赵光, 张爽浩, 冯晓毅, 彭进业 2016 65 230301
Google Scholar
Cao Z W, Zhao G, Zhang S H, Feng X Y, Peng J Y 2016 Acta Phys. Sin. 65 230301
Google Scholar
[13] Chen J P, Zhang C, Liu Y, Jiang C, Zhang W J, Hu X L, Guan J Y, Yu Z W, Xu H, Lin J, Li M J, Chen H, Li H, You, L X, Wang Z, Wang X B, Zhang Q, Pan J W 2020 Phys. Rev. Lett. 124 070501
Google Scholar
[14] 龙桂鲁, 潘栋 2021 信息通信技术与政策 7 7
Google Scholar
Long G L, Pan D 2021 Telecommunications Network Technology 7 7
Google Scholar
[15] Sheng Y B, Guo F G, Long G L 2010 Phys Rev. A 82 032318
Google Scholar
[16] Hong C H, Heo J, Lim J I, Yang H J 2014 Chin. Phys. B 23 090309
Google Scholar
[17] Wang X L, Cai X D, Su Z E, Cheng M C, Wu D, Li L, Liu N L, Lu C Y, Pan J W 2015 Nature 518 516
Google Scholar
[18] Xu L 2020 Modern Phys Lett. B 34 2050353
Google Scholar
[19] 彭承志, 潘建伟 2016 中国科学院院刊 31 1096
Peng C Z, Pan J W 2016 Bulletin of Chinese Academy of Sciences 31 1096
[20] Liao S K, Cai W Q 2018 Phys. Rev. Lett. 120 030501
Google Scholar
[21] 赖俊森, 赵文玉, 张海懿 2021 信息通信技术与政策 7 6
Google Scholar
Lai J S, Zhao W Y, Zhang H Y 2021 Telecommunications Network Technology 7 6
Google Scholar
[22] 聂敏, 张帆, 杨光, 张美玲, 孙爱晶, 裴昌幸 2021 70 040303
Google Scholar
Nie M, Zhang F, Yang G, Zhang M L, Sun A J, Pei C X 2021 Acta Phys. Sin. 70 040303
Google Scholar
[23] 杨光, 廉保旺, 聂敏 2015 64 010303
Google Scholar
Yang G, Lian B W, Nie M 2015 Acta Phys. Sin. 64 010303
Google Scholar
[24] 杨光, 廉保旺, 聂敏 2015 64 240304
Google Scholar
Yang G, Lian B W, Nie M 2015 Acta Phys. Sin. 64 240304
Google Scholar
[25] Briegel H J, Raussendorf R 2001 Phys. Rev. Lett. 86 910
Google Scholar
[26] Pan J W, Bouwmeester D, Weinfurter H, Zeilinger A 1998 Phys. Rev. Lett. 80 3891
Google Scholar
[27] Dotsenko I S, Korobka R 2018 Commun. Theor. Phys. 69 143
Google Scholar
[28] Li Y H, Li X L, Nie L P, Sang M H 2016 Int. J. Theor. Phys. 55 1820
Google Scholar
[29] Tao Y X, Xu J, Zhang Z C 2013 Chin. Phys. B 22 090311
Google Scholar
[30] Espoukeh P, Pedram P 2014 Int. J. Theor. Phys. 13 1789
[31] Du Z L, Li X L, Liu X J 2020 Int. J. Theor. Phys. 59 622
Google Scholar
[32] Gao X Q, Zhang Z C, Gong Y X, Sheng B, Yu X T 2017 J. Opt. Soc. Am. B-Opt. Phys. 34 142
Google Scholar
[33] Cai X F, Yu X T, Shi L H, Zhang Z C 2014 Front. Phys. 9 646
Google Scholar
[34] Xiong P Y, Yu X T, Zhang Z C, Zhan H T, Hua J Y 2017 Front. Phys. 12 1
[35] Wang K, Yu X T, Lu S L, Gong X Y 2014 Phys Rev. A 89 022329
Google Scholar
[36] Tao Y, Zhang Q, Zhang J, Yin J, Zhao Z, Zukowski M, Chen Z B, Pan J W 2005 Phys. Rev. Lett. 95 240406
Google Scholar
[37] 郭肖 2020 硕士学位论文 (西安: 西安电子科技大学 )
Guo X 2020 M. S. Dissertation (Shannxi: Xidian University) (in Chinese)
[38] 聂敏, 王超旭, 杨光, 张美玲, 孙爱晶, 裴昌幸 2021 70 030301
Google Scholar
Nie M, Wang C X, Yang G, Sun A J, Pei C X 2021 Acta Phys. Sin. 70 030301
Google Scholar
[39] 张秀再, 徐茜, 刘邦宇 2020 光学学报 40 0327001
Google Scholar
Zhang X Z, Xu Q, Liu B Y 2020 Acta Optica Sinica 40 0327001
Google Scholar
[40] Xu J, Chen X G, Xiao H W, Wang P X, Ma M 2021 Appl. Sci. 11 10869
Google Scholar
[41] Cabello A 2000 Phys. Rev. Lett. 85 5635
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4603
- PDF Downloads: 69
- Cited By: 0
