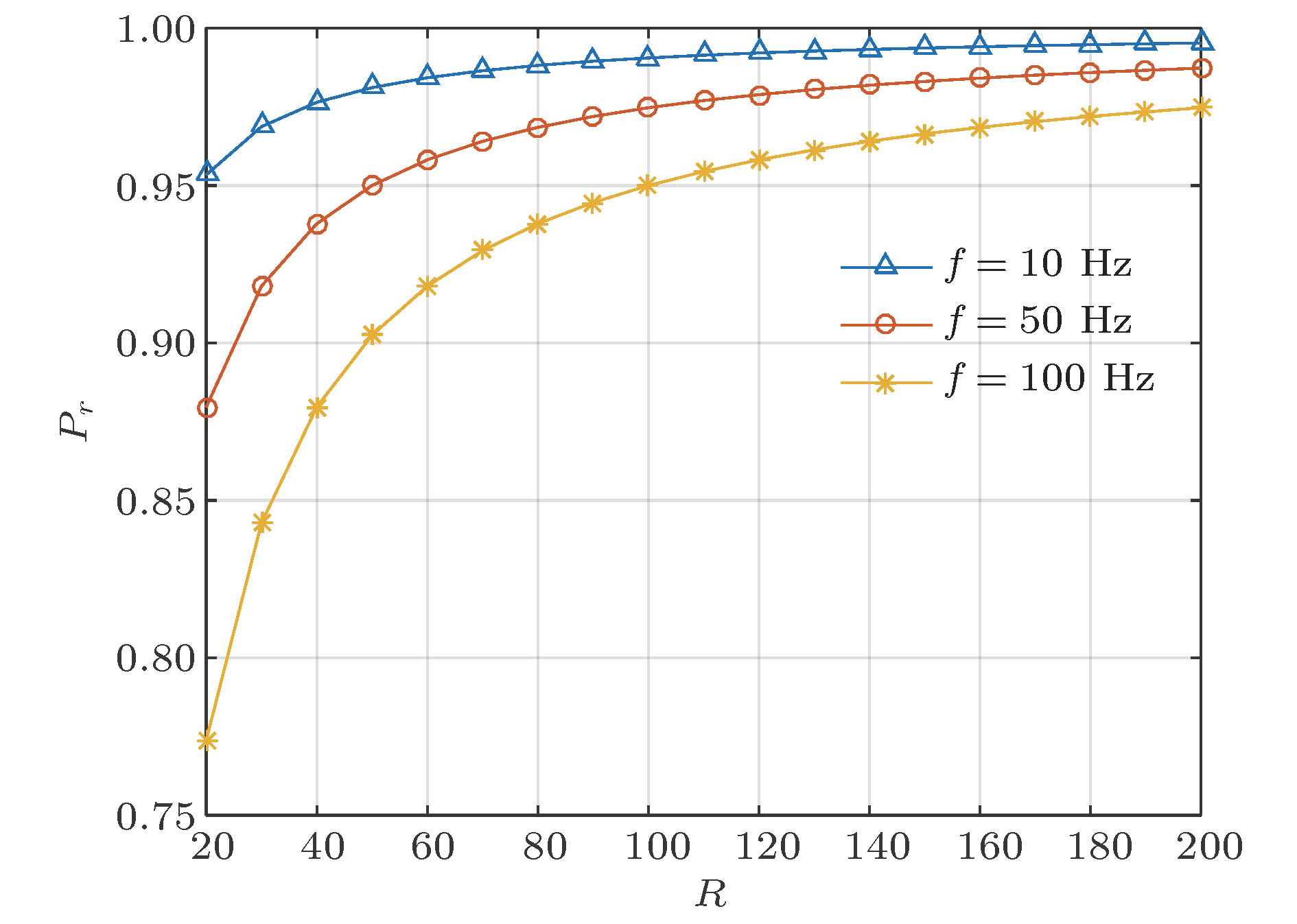
-
自由空间中的量子通信会不同程度上受到雾霾、沙尘等自然环境的干扰. 为了研究提升此类干扰下量子通信的性能, 本文分析了背景干扰下单量子态信道随时间演化的性能变化, 并根据袋鼠纠缠跳跃模型(KEHM), 提出了基于KEHM的量子状态自适应跳变通信策略, 对其性能参数进行仿真. 仿真结果表明, 采取量子状态跳变, 在背景量子噪声的平均功率与量子信号平均功率的比值为5的情况下, 量子误比特率随着量子态跳频率从1增大到15, 由0.4524降低到0.1116; 当单量子态传输成功率0.95, 量子比特率大于200 qubit/s时, 不同态跳频率下量子比特的成功传输概率均大于0.97. 当发送端信号源平均量子数足够大且接收端接收效率趋近于1时, 量子态的通过率也趋近于1; 采取量子态跳自适应控制策略, 能够进一步降低系统的误码率.Quantum communication in free space will be disturbed by natural environment such as fog and dust. However, to build a global quantum satellite wide area communication network, we must solve the problem of 24-h all-weather communication between satellite and earth. With the evolution of time, the degree of interference becomes deeper. In order to improve the performance of quantum communication under such an interference, in this paper we analyze the change of single quantum state channel over time under the background interference, and propose an quantum state-hopping communication strategy based on the kangaroo entanglement hopping model (KEHM), and simulate the performance and parameters of the strategy. Kangaroos are social animals. When they are frightened, they will jump synchronously in the same way with the same step length, height and frequency. According to this model, we make the two communicating parties realize synchronous quantum state jump according to the prearranged pattern. The simulations show that when the ratio between the average power of background quantum noise and the average power of quantum signal is 5, the quantum bit error rate decreases from 0.4524 to 0.1116 with the quantum state hopping frequency increasing from 1 to 15. When the single quantum state transmission success rate is 0.95 and the quantum bit rate is greater than 200 qubit/s, the probabilities of successful transmission of quantum bits at different state hopping frequencies are greater than 0.97. When the quantum reception efficiency of the receiver is 0.8, the quantum state pass rate increases from 0.3667 to 0.9986 with the average quantum number of the source increasing from 1 to 10. When the average quantum number of the source is 6, the passing rate of quantum state increases from 0.6262 to 0.9855 with the quantum receiving efficiency of the receiver increasing from 0.2 to 0.99. However, if the average quantum number of the transmitter is large enough and the receiving efficiency of the receiver is close to 1, the passing rate of the quantum state is also close to 1. The adaptive control strategy of quantum state hopping is based on real-time quantum channel state detection. Its core idea is to remove the quantum states which are seriously disturbed from the quantum state hopping set, and to realize the synchronous hopping of communication parties on the quantum states with low interference. Adopting the strategy of quantum state hopping adaptive control can further reduce the quantum bit error rate of the system. The error rate gain of adaptive control system increases with the increase of the success probability of processing the disturbed quantum state. When the probability of processing the disturbed quantum state is 0.95, the system error rate gain can reach 1.301. The performance of quantum state hopping system is improved obviously. To sum up, the adaptive quantum state-hopping communication strategy based on the kangaroo entanglement hopping model proposed in this paper greatly enhances the comprehensive immunity of the system and ensures the security of quantum information network, and provides an important reference for the healthy development of wide-area quantum satellite communication network in the future.
-
Keywords:
- free space quantum communication /
- background quantum noise /
- quantum state hopping /
- bit error rate
[1] Jin X M, Ren J G, Yang B 2010 Nat. Photonics 4 376
Google Scholar
[2] Alessandro F, Rupert U, Thomas H, Matteo N, Robert P, Thomas S, Felix T, Thomas J, Anton Z 2009 Nat. Phys. 5 389
Google Scholar
[3] Ma X S, Thomas H, Thomas S, Wang D Q, Sebastian K, William Nr, Bernhard W, Alexandra M, Johannes K, Elena A, Vadim M, Thomas J, Rupert U, Anton Z 2012 Nature 489 269
Google Scholar
[4] Wang J Y, Yang B, Liao S K, Zhang L, Shen Q, Hu X F, Wu J C, Yang S J, Jiang H, Tang Y L, Zhong B, Liang H, Liu W Y, Hu Y H, Huang Y M, Qi B, Ren J G, Pan G S, Yin J, Jia J J, Chen Y A, Chen K, Peng C Z, Pan J W 2013 Nat. Photonics 7 387
Google Scholar
[5] Wang X L, Cai X D, Su Z E 2015 Nature 518 516
Google Scholar
[6] Davide E B, Timothy C, Ralph, Ivette F, Thomas J, Mohsen R 2014 Phys. Rev. D 90 045041
Google Scholar
[7] Liao S K, Yong H L, Liu C, Shentu G L, Li D D, Lin J, Dai H, Zhao S Q, Li B, Guan J Y, Chen W, Gong Y H, Li Y, Lin Z H, Pan G S, Pelc S J, Fejer M M, Zhang W Z, Liu W Y, Yin J, Ren J G, Wang X B, Zhang Q, Peng C Z, Pan J W 2017 Nat. Photonics 11 509
Google Scholar
[8] 聂敏, 尚鹏钢, 杨光, 张美玲, 裴昌幸 2014 63 240303
Google Scholar
Nie M, Shang P G, Yang G, Zhang M L, Pei C X 2014 Acta Phys. Sin. 63 240303
Google Scholar
[9] 聂敏, 任杰, 杨光, 张美玲, 裴昌幸 2015 64 150301
Google Scholar
Nie M, Ren J, Yang G, Zhang M L, Pei C X 2015 Acta Phys. Sin. 64 150301
Google Scholar
[10] Ivan C, Andrea T, Alberto D, Francesca G, Ruper U, Giuseppe V, Paolo V 2012 Phys. Rev. Lett. 109 200502
Google Scholar
[11] 聂敏, 常乐, 杨光, 张美玲, 裴昌幸 2017 光子学报 46 0701002
Nie M, Chang L, Yang G, Zhang M L, Pei C X 2017 Acta Photon. Sin. 46 0701002
[12] 聂敏, 任家明, 杨光, 张美玲, 裴昌幸 2016 光子学报 45 0927004
Nie M, Ren J M, Yang G, Zhang M L, Pei C X 2016 Acta Photon. Sin. 45 0927004
[13] 聂敏, 唐守荣, 杨光, 张美玲, 裴昌幸 2017 66 070302
Google Scholar
Nie M, Tang S R, Yang G, Zhang M L, Pei C X 2017 Acta Phys. Sin. 66 070302
Google Scholar
[14] 聂敏, 唐守荣, 杨光, 张美玲, 裴昌幸 2017 光子学报 46 1206002
Nie M, Tang S R, Yang G, Zhang M L, Pei C X 2017 Acta Photon. Sin. 46 1206002
[15] 聂敏, 任家明, 杨光, 张美玲, 裴昌幸 2016 65 190301
Google Scholar
Nie M, Ren J M, Yang G, Zhang M L, Pei C X 2016 Acta Phys. Sin. 65 190301
Google Scholar
[16] 聂敏, 石力, 杨光, 裴昌幸 2017 通信学报 38 2017092
Nie M, Shi L, Yang G, Pei C X 2017 J. Communs. 38 2017092
[17] 张永德 2010 量子力学 (北京: 科学出版社) 第343页
Zhang Y D 2010 Quantum Mechanics (Beijing: Science Press) p343 (in Chinese)
[18] 张永德 2010 高等量子力学 (北京: 科学出版社) 第24页
Zhang Y D 2010 Advanced Quantum Mechanics (Beijing: Science Press) p24 (in Chinese)
[19] 马科 L 著 (周万幸, 吴鸣亚, 胡明春, 金林 译) 2013 量子雷达 (北京: 电子工业出版社) 第15—17页
Marco L (translated bu Zhou W X, Wu M Y, Hu M C, Jin L) 2013 Quantum Radar (Beijing: Publishing House of Electronics Industry) pp15−17 (in Chinese)
[20] 尹浩, 韩阳 2013 量子通信原理与技术 (北京: 电子工业出版社) 第100页
Yin H, Han Y 2013 Quantum Communication Principle and Technology (Beijing: Publishing House of Electronics Industry) p100 (in Chinese)
-
图 3 量子误比特率与量子态跳频率及
${K_{JS}}$ 的关系Fig. 3. Relationship between quantum bit error rate, quantum state hopping frequency and
${K_{JS}}$ 
图 4 量子比特成功传输概率与量子比特率的关系
Fig. 4. Relationship between the probability of successful quantum bit transmission and the quantum bit rate
图 5 量子态通过率与接收端量子接收效率及信号源平均量子数的关系
Fig. 5. Relationship between the quantum state pass rate and the receiver's quantum reception efficiency and the average quantum number of the signal source
图 6 量子态数目、被严重干扰的概率与平均自适应处理时间的关系
Fig. 6. Relationship between the number of quantum states, the probability of serious interference, and the mean adaptive processing time
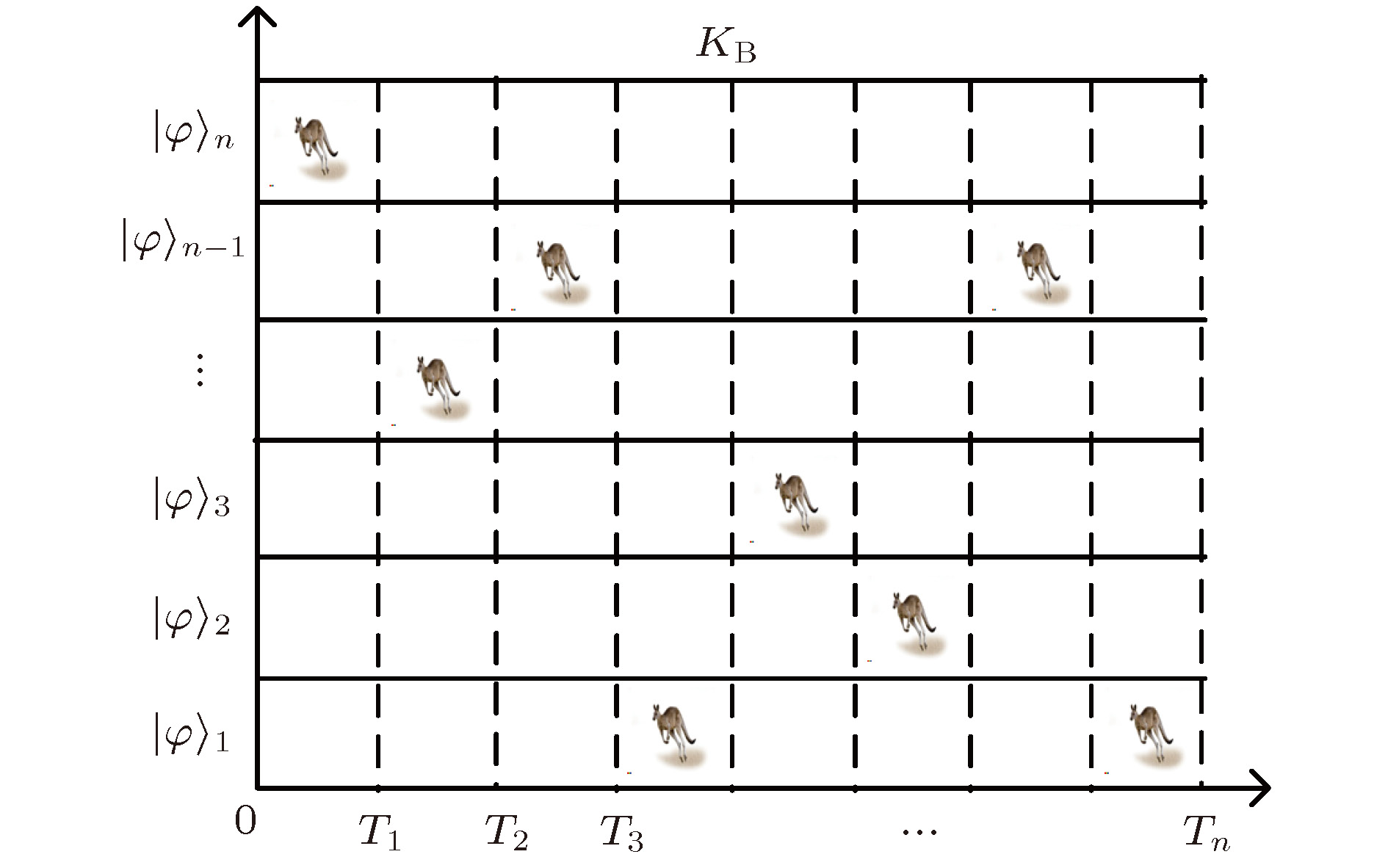
表 1 不同时刻通信双方量子跳跃状态
Table 1. Quantum hopping states of communication parties at different moments
时刻 $T$ 状态 $\left| \phi \right\rangle $ 0—T1 ${\left| \phi \right\rangle _n}$ T1—T2 ${\left| \phi \right\rangle _{n-2}}$ T2—T3 ${\left| \phi \right\rangle _{n - 1}}$ T3—T4 ${\left| \phi \right\rangle _1}$ $ \cdots $ $ \cdots $ Tn–1—Tn ${\left| \phi \right\rangle _1}$ 
下载: 导出CSV
-
[1] Jin X M, Ren J G, Yang B 2010 Nat. Photonics 4 376
Google Scholar
[2] Alessandro F, Rupert U, Thomas H, Matteo N, Robert P, Thomas S, Felix T, Thomas J, Anton Z 2009 Nat. Phys. 5 389
Google Scholar
[3] Ma X S, Thomas H, Thomas S, Wang D Q, Sebastian K, William Nr, Bernhard W, Alexandra M, Johannes K, Elena A, Vadim M, Thomas J, Rupert U, Anton Z 2012 Nature 489 269
Google Scholar
[4] Wang J Y, Yang B, Liao S K, Zhang L, Shen Q, Hu X F, Wu J C, Yang S J, Jiang H, Tang Y L, Zhong B, Liang H, Liu W Y, Hu Y H, Huang Y M, Qi B, Ren J G, Pan G S, Yin J, Jia J J, Chen Y A, Chen K, Peng C Z, Pan J W 2013 Nat. Photonics 7 387
Google Scholar
[5] Wang X L, Cai X D, Su Z E 2015 Nature 518 516
Google Scholar
[6] Davide E B, Timothy C, Ralph, Ivette F, Thomas J, Mohsen R 2014 Phys. Rev. D 90 045041
Google Scholar
[7] Liao S K, Yong H L, Liu C, Shentu G L, Li D D, Lin J, Dai H, Zhao S Q, Li B, Guan J Y, Chen W, Gong Y H, Li Y, Lin Z H, Pan G S, Pelc S J, Fejer M M, Zhang W Z, Liu W Y, Yin J, Ren J G, Wang X B, Zhang Q, Peng C Z, Pan J W 2017 Nat. Photonics 11 509
Google Scholar
[8] 聂敏, 尚鹏钢, 杨光, 张美玲, 裴昌幸 2014 63 240303
Google Scholar
Nie M, Shang P G, Yang G, Zhang M L, Pei C X 2014 Acta Phys. Sin. 63 240303
Google Scholar
[9] 聂敏, 任杰, 杨光, 张美玲, 裴昌幸 2015 64 150301
Google Scholar
Nie M, Ren J, Yang G, Zhang M L, Pei C X 2015 Acta Phys. Sin. 64 150301
Google Scholar
[10] Ivan C, Andrea T, Alberto D, Francesca G, Ruper U, Giuseppe V, Paolo V 2012 Phys. Rev. Lett. 109 200502
Google Scholar
[11] 聂敏, 常乐, 杨光, 张美玲, 裴昌幸 2017 光子学报 46 0701002
Nie M, Chang L, Yang G, Zhang M L, Pei C X 2017 Acta Photon. Sin. 46 0701002
[12] 聂敏, 任家明, 杨光, 张美玲, 裴昌幸 2016 光子学报 45 0927004
Nie M, Ren J M, Yang G, Zhang M L, Pei C X 2016 Acta Photon. Sin. 45 0927004
[13] 聂敏, 唐守荣, 杨光, 张美玲, 裴昌幸 2017 66 070302
Google Scholar
Nie M, Tang S R, Yang G, Zhang M L, Pei C X 2017 Acta Phys. Sin. 66 070302
Google Scholar
[14] 聂敏, 唐守荣, 杨光, 张美玲, 裴昌幸 2017 光子学报 46 1206002
Nie M, Tang S R, Yang G, Zhang M L, Pei C X 2017 Acta Photon. Sin. 46 1206002
[15] 聂敏, 任家明, 杨光, 张美玲, 裴昌幸 2016 65 190301
Google Scholar
Nie M, Ren J M, Yang G, Zhang M L, Pei C X 2016 Acta Phys. Sin. 65 190301
Google Scholar
[16] 聂敏, 石力, 杨光, 裴昌幸 2017 通信学报 38 2017092
Nie M, Shi L, Yang G, Pei C X 2017 J. Communs. 38 2017092
[17] 张永德 2010 量子力学 (北京: 科学出版社) 第343页
Zhang Y D 2010 Quantum Mechanics (Beijing: Science Press) p343 (in Chinese)
[18] 张永德 2010 高等量子力学 (北京: 科学出版社) 第24页
Zhang Y D 2010 Advanced Quantum Mechanics (Beijing: Science Press) p24 (in Chinese)
[19] 马科 L 著 (周万幸, 吴鸣亚, 胡明春, 金林 译) 2013 量子雷达 (北京: 电子工业出版社) 第15—17页
Marco L (translated bu Zhou W X, Wu M Y, Hu M C, Jin L) 2013 Quantum Radar (Beijing: Publishing House of Electronics Industry) pp15−17 (in Chinese)
[20] 尹浩, 韩阳 2013 量子通信原理与技术 (北京: 电子工业出版社) 第100页
Yin H, Han Y 2013 Quantum Communication Principle and Technology (Beijing: Publishing House of Electronics Industry) p100 (in Chinese)
下载:
计量
- 文章访问数: 6610
- PDF下载量: 39
- 被引次数: 0
