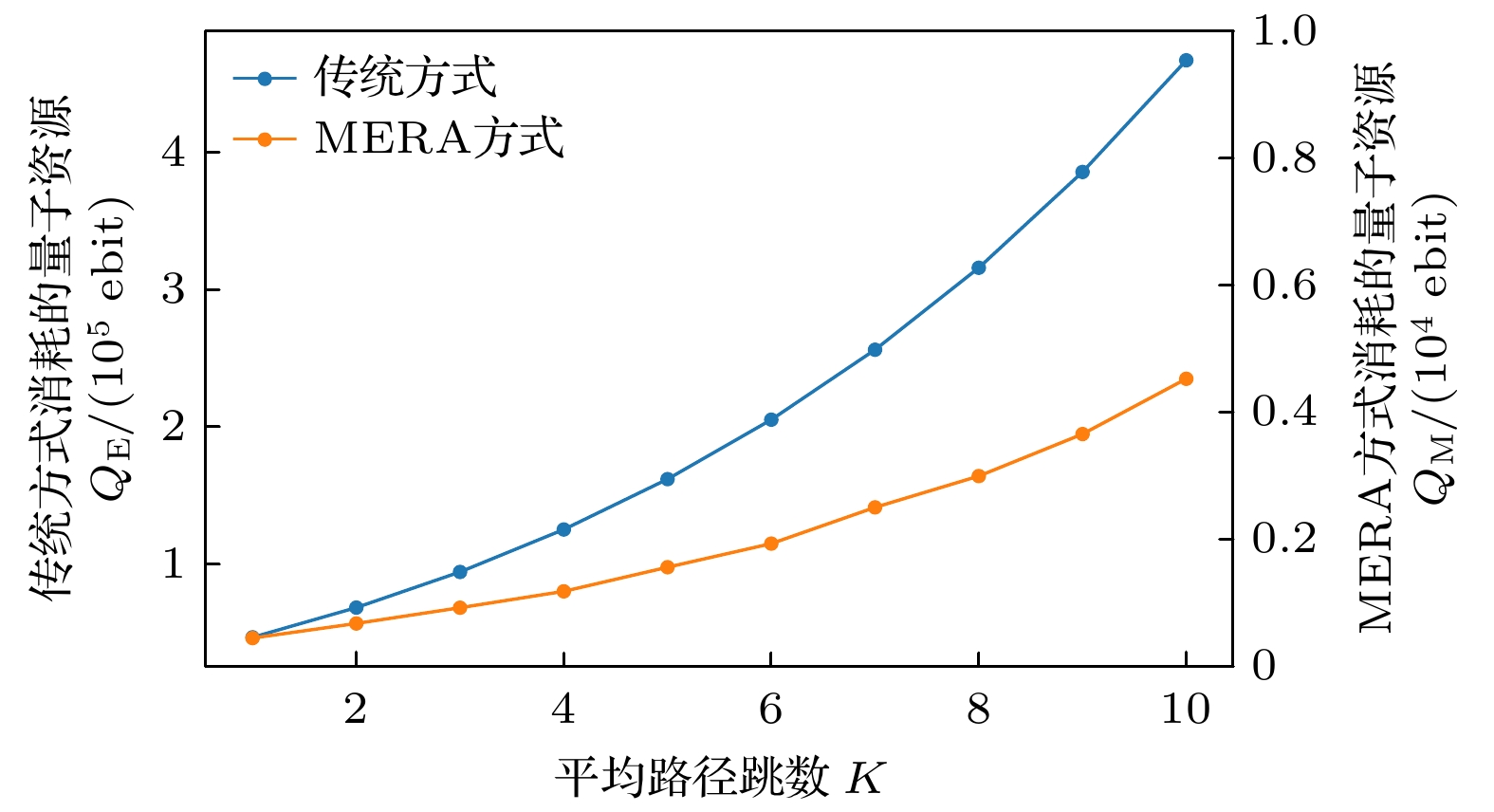
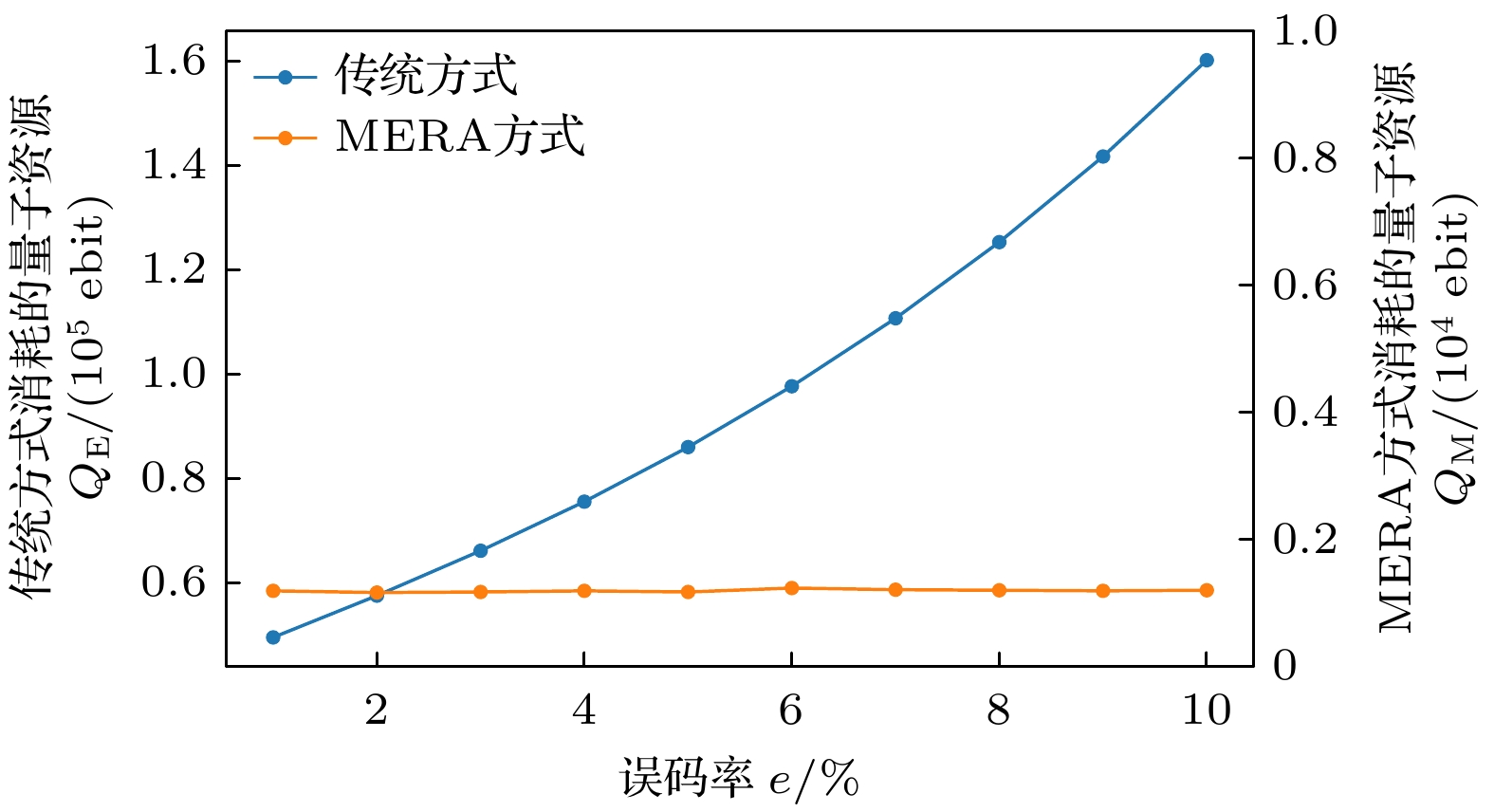
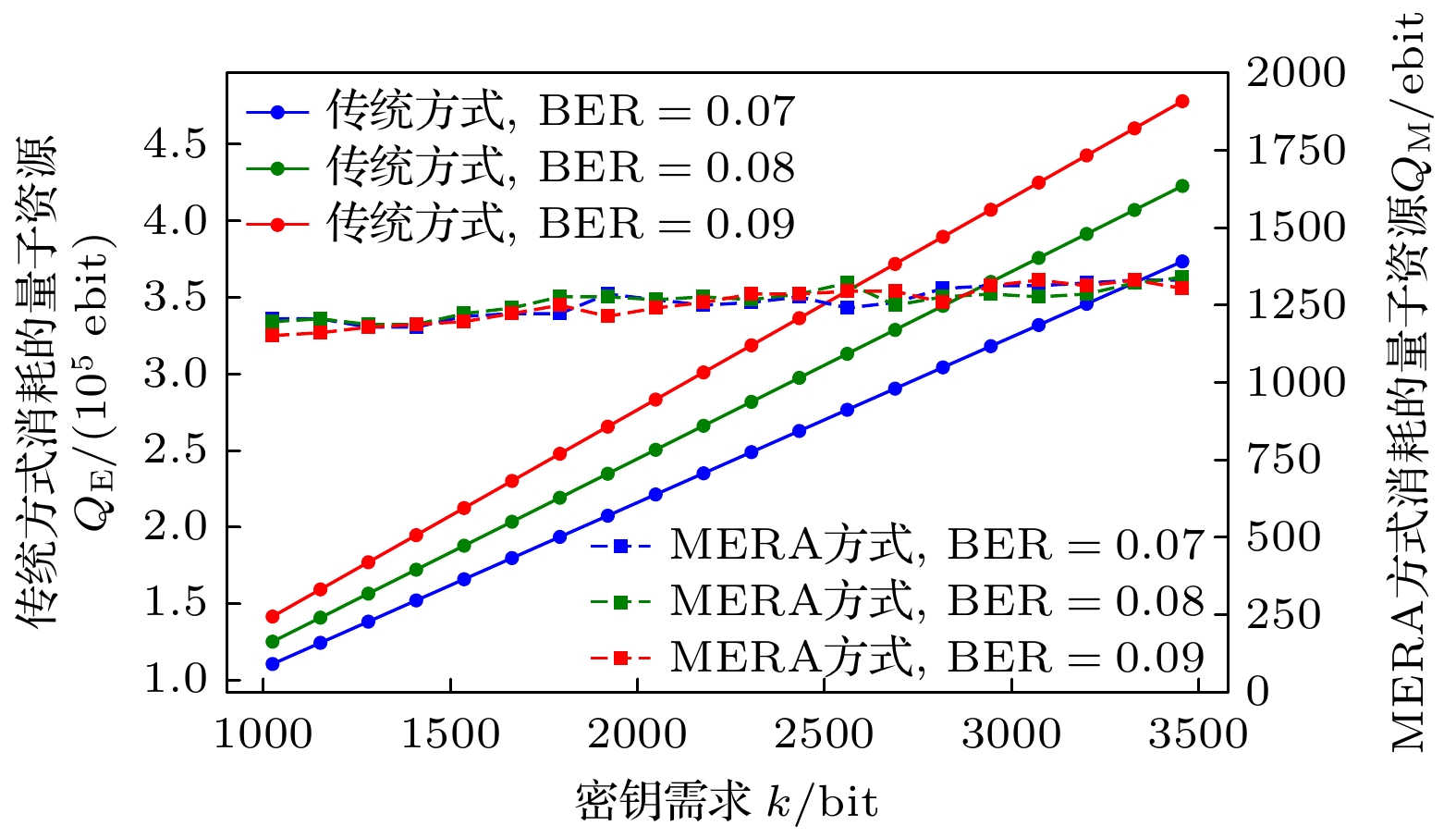
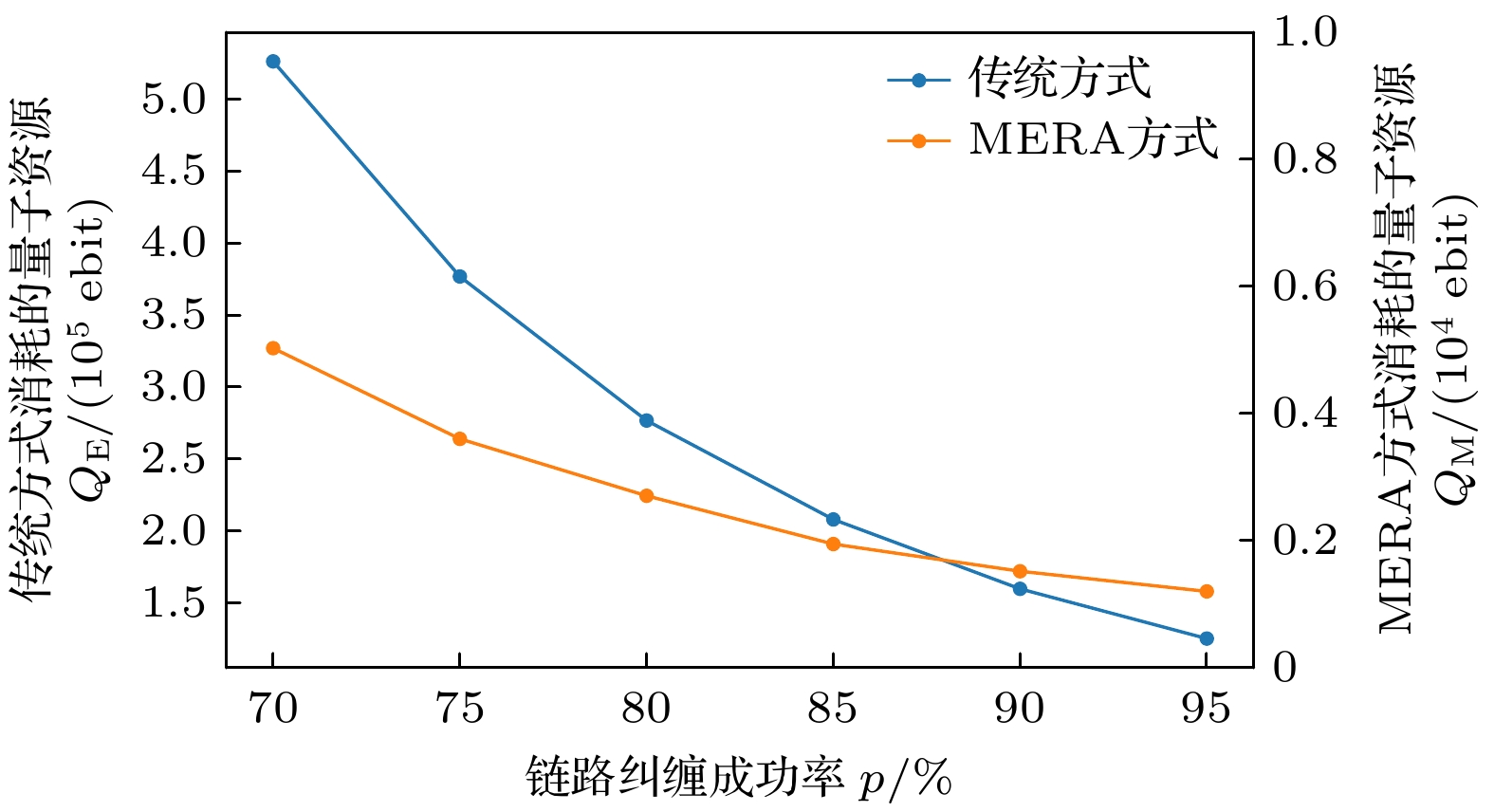
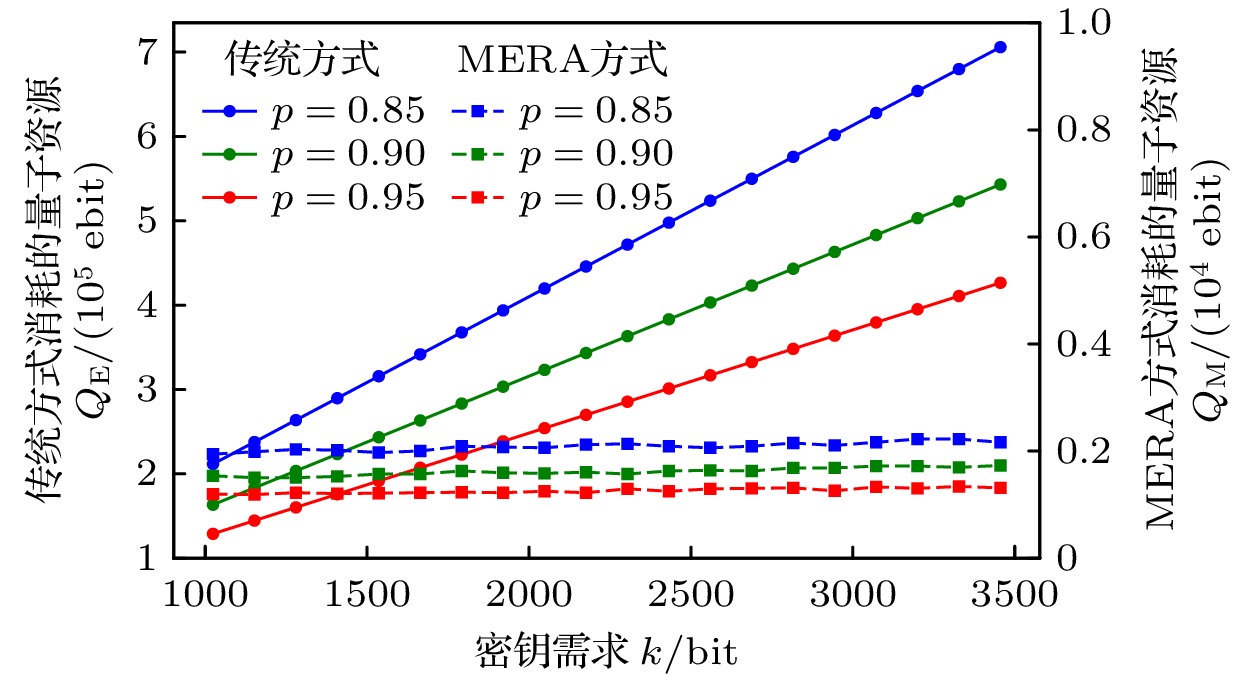
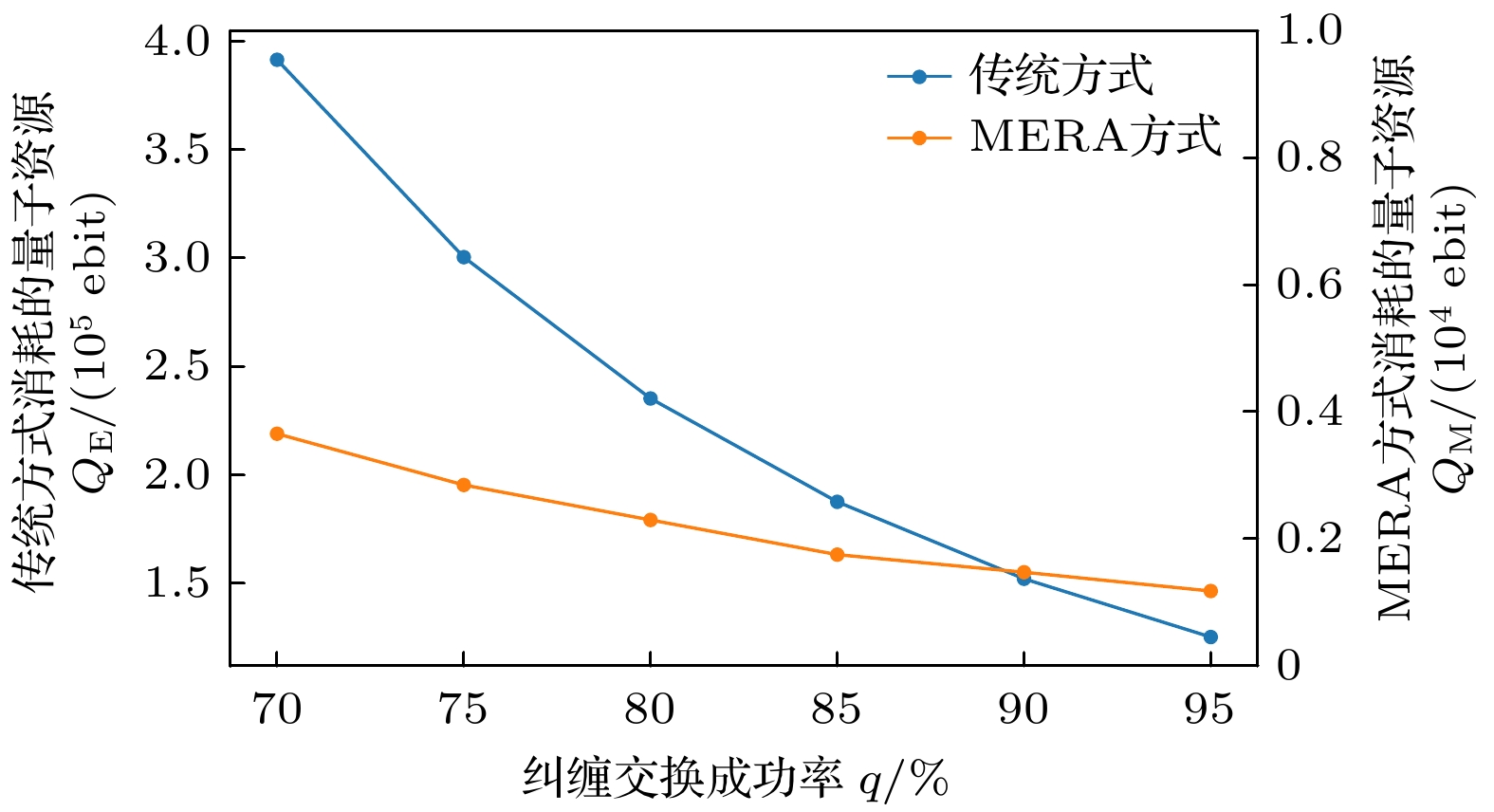
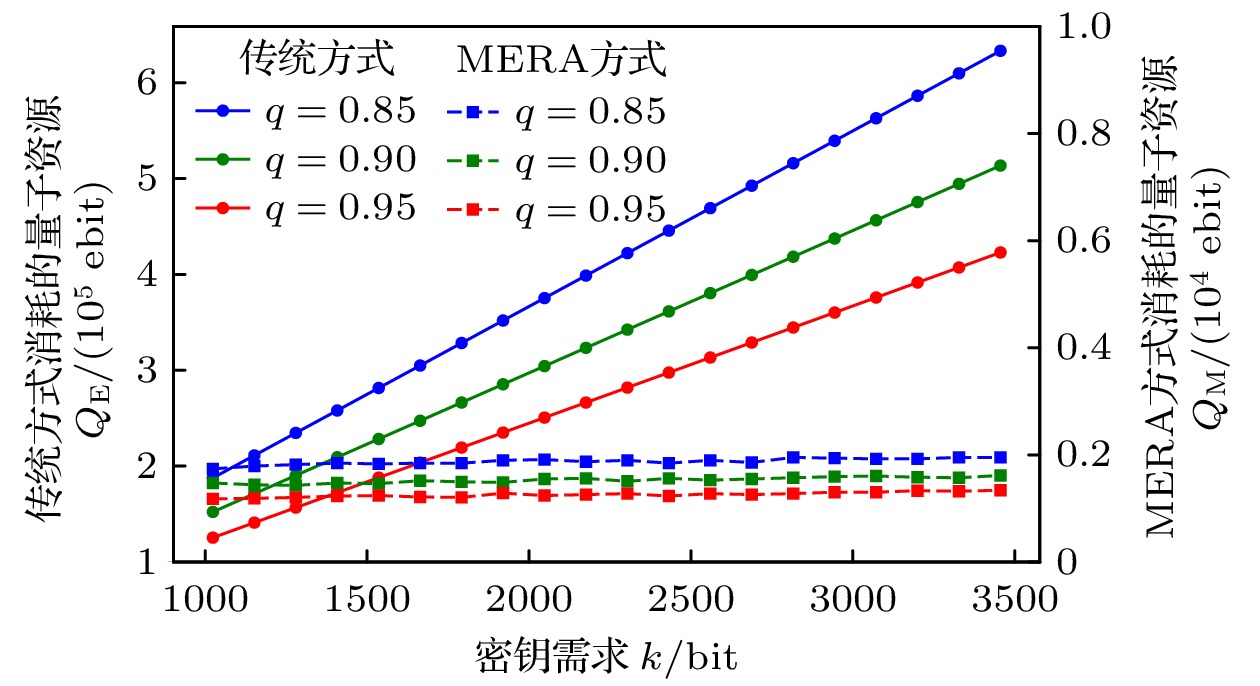
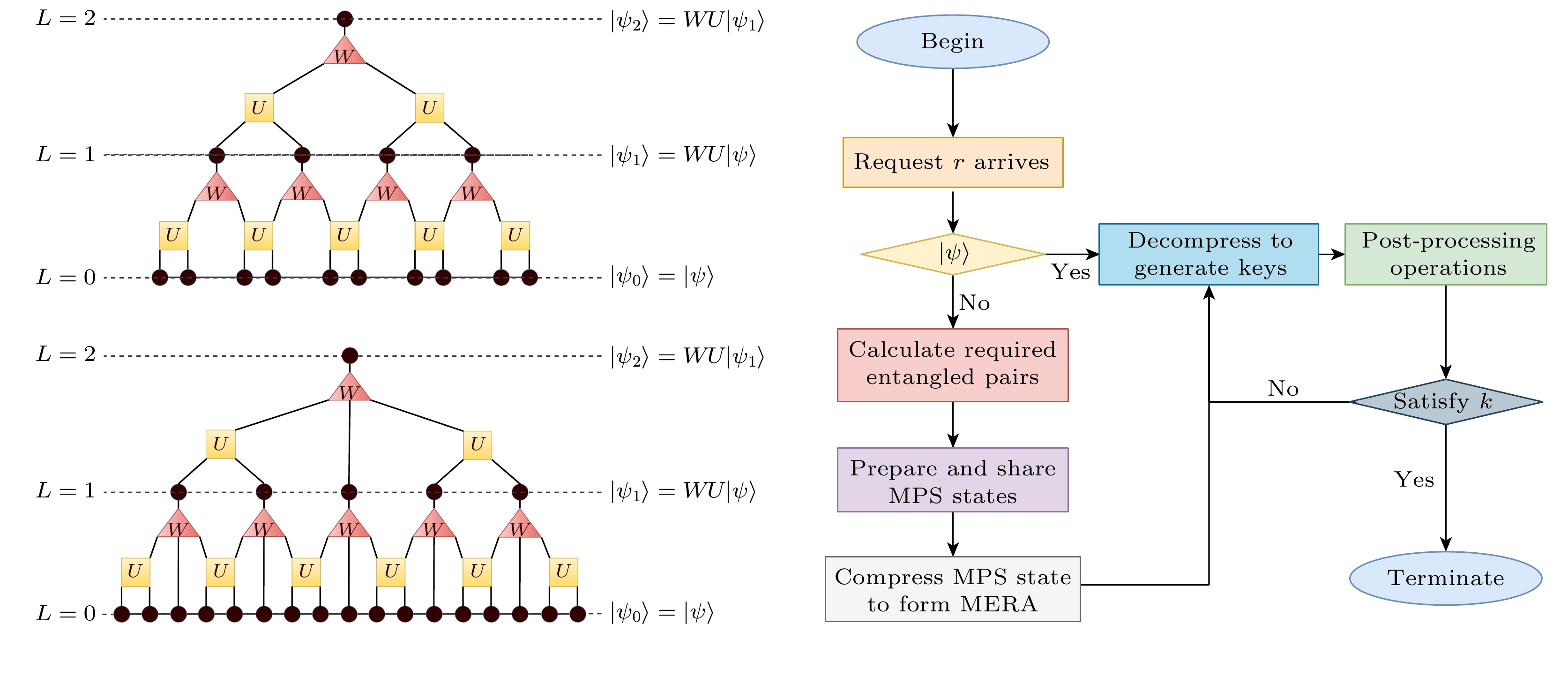
-
Quantum Key Distribution (QKD) is a pivotal technology in the field of secure communications, leveraging the principles of quantum mechanics to enable theoretically unbreakable encryption. However, despite its promise, QKD faces significant challenges in achieving large-scale deployment. The primary hurdle lies in the scarcity of quantum resources, especially entangled photon pairs, which are fundamental to protocols such as Ekert91. In traditional QKD implementations, only a fraction of the entangled pairs generated contribute to raw key production, leading to substantial inefficiencies and resource wastage. Addressing this limitation is crucial to the advancement and scalability of QKD networks. This paper introduces an innovative approach to QKD by integrating the Multiscale Entanglement Renormalization Ansatz (MERA), a technique originally developed for many-body quantum systems. By utilizing MERA's hierarchical structure, the proposed method not only improves the efficiency of entanglement distribution but also reduces the consumption of quantum resources. Specifically, MERA compresses many-body quantum states into lower-dimensional representations, allowing for the transmission and storage of entanglement in a more efficient manner. This compression significantly reduces the number of qubits required, optimizing both entanglement utilization and storage capacity in quantum networks. To evaluate the performance of this method, we conducted simulations under standardized conditions. The simulations assumed a 1024-bit encryption request, an 8% error rate, an average path length of 4 hops in the quantum network, and a 95% success rate for both link entanglement generation and entanglement swapping operations. These parameters mirror realistic physical conditions found in contemporary QKD networks. The results demonstrate that the MERA-based approach saves an impressive 124,151 entangled pairs compared to traditional QKD protocols. This substantial reduction in resource consumption underscores the potential of MERA to revolutionize the efficiency of QKD systems without compromising security. Importantly, the security of the key exchange process remains intact, as the method inherently adheres to the principles of quantum mechanics, particularly the no-cloning theorem and the use of randomness in decompression layers. The paper concludes that MERA not only enhances the scalability of QKD by optimizing quantum resource allocation but also maintains the security guarantees essential for practical cryptographic applications. By integrating MERA into existing QKD frameworks, we can significantly lower the resource overhead, making large-scale, secure quantum communication more feasible. These findings contribute a new dimension to the field of quantum cryptography, suggesting that advanced quantum many-body techniques like MERA hold the potential to unlock the full potential of quantum networks in real-world scenarios. 
-
Keywords:
- Quantum key distribution /
- Multi-scale entanglement renormalization ansatz /
- Resource utilization /
- Security
-
图 1 MERA结构: (a) 二元MERA; (b) 三元MERA; (c) 解纠缠算符U; (d) 等距映射W
Figure 1. The structure of MERA: (a) Binary MERA; (b) Ternary MERA; (c) Disentangling operator U; (d) Isometric mapping W.
图 2 U与$ |00\rangle, |01\rangle, |10\rangle, |11\rangle $的映射关系
Figure 2. The mapping relationship between U and $ |00\rangle, |01\rangle, |10\rangle, |11\rangle $.
图 3 W与$ |0\rangle, |1\rangle $的映射关系
Figure 3. The mapping relationship between W and $ |0\rangle, |1\rangle $.
图 4 网络结构
Figure 4. Network structure.
图 5 量子密钥分发流程图
Figure 5. Quantum key distribution flowchart.
图 6 状态表
Figure 6. State table.
图 7 传统方式与MERA方式下量子资源消耗随需求变化的关系
Figure 7. Relationship between quantum resource consumption and demand in traditional versus MERA.
图 8 传统方式与MERA方式下经典资源消耗随需求变化的关系
Figure 8. Relationship between classical resource consumption and demand in traditional versus MERA.
图 9 传统方式与MERA方式下总资源消耗随需求变化的关系
Figure 9. The relationship between total resource consumption and demand in traditional versus MERA.
图 10 所需量子资源随平均路径跳数从1到10的变化情况
Figure 10. Variation in quantum resource requirements as average path length increases from 1 to 10.
图 11 平均路径跳数为4、5、6时, 量子资源消耗随请求量的变化
Figure 11. Quantum Resource Variation with Request Volume at Average Path Lengths of 4, 5, and 6.
图 12 误码率从1%—10%变化时, 所需量子资源的增长情况
Figure 12. Variation in Quantum Resource Requirements as Error Rate Changes from 1% to 10%.
图 13 误码率为7%、8%、9%时, 量子资源随请求量变化的情况
Figure 13. Quantum Resource Variation with Request Volume at Error Rates of 7%, 8%, and 9%.
图 14 链路纠缠成功率从70%到95%变化时, 所需量子资源数量的变化趋势
Figure 14. Quantum Resource Variation as Link Entanglement Success Rate Ranges from 70% to 95%.
图 15 链路纠缠成功率分别取85%、90%、95%时, 量子资源的变化趋势
Figure 15. Quantum Resource Variation at Link Entanglement Success Rates of 85%, 90%, and 95%.
图 16 纠缠交换成功率从70%到95%变化时, 所需量子资源数量的变化趋势
Figure 16. Quantum Resource Variation as Entanglement Swapping Success Rate Ranges from 70% to 95%.
图 17 纠缠交换成功率为85%、90%、95%时, 量子资源的变化趋势
Figure 17. Quantum Resource Variation at Entanglement Swapping Success Rates of 85%, 90%, and 95%.
表 1 网络请求属性及其取值范围
Table 1. Network request attributes and their value ranges.
属性 描述 取值范围 S 发送方 N/A D 接收方 N/A k 需求量 $ [1024, 4096] $ P 优先级 $ [1, 5] $ $ \Delta t $ 可接受时延 $ [1, 60] $ 
DownLoad: CSV
-
[1] Wootters W K, Zurek W H 1982 Nature 299 802
Google Scholar
[2] Peev M, Pacher C, Alléaume R 2009 New J. Phys. 11 075001
Google Scholar
[3] Dianati M, Alléaume R, Gagnaire M 2008 Security Commun. Networks 1 57
Google Scholar
[4] Aguado A, Lopez V, Lopez D 2019 IEEE Commun. Mag. 57 20
[5] Donetti L, Hurtado P I, Munoz M A 2005 Phys. Rev. Lett. 95 188701
Google Scholar
[6] Li Z, Xue K P, Li J 2023 IEEE Commun. Surv. Tutor. 25 2133
Google Scholar
[7] Pant M, Krovi H, Towsley D 2019 npj Quantum Inf. 5 25
Google Scholar
[8] Shi S, Zhang X, Qian C 2024 IEEE/ACM Trans. Netw. 32 2205
Google Scholar
[9] Li J, Wang M, Xue K P 2022 IEEE Trans. Commun. 70 6748
Google Scholar
[10] Gu H Y, Li Z Y 2024 IEEE/ACM Trans. Netw. 1 125
[11] Ekert A 1991 Phys. Rev. Lett. 67 661
Google Scholar
[12] Bennett C H, Brassard G, Mermin N D 1992 Phys. Rev. Lett. 68 557
Google Scholar
[13] Li C, Li T, Liu Y X 2021 npj Quantum Inf. 7 10
Google Scholar
[14] 赖红 2023 72 149
Lai H 2023 Acta Phys. Sin. 72 149
[15] Kim Y H, Kulik S P, Shih Y 2001 Phys. Rev. Lett. 86 1370
Google Scholar
[16] Cincio L, Dziarmaga J, Rams M M 2008 Phys. Rev. Lett. 100 240603
Google Scholar
[17] Lai H, Pieprzyk J, Pan L 2022 Phys. Rev. A 106 052403
Google Scholar
[18] Pirandola S, García-Patrón R, Braunstein S L 2009 Phys. Rev. Lett. 102 050503
Google Scholar
[19] Pirandola S, Laurenza R, Ottaviani C 2017 Nat. Commun. 8 1500
Google Scholar
[20] Wehner S, Elkouss D, Hanson R 2018 Science 362 9288
Google Scholar
[21] Bernien H, Hensen B, Pfaff W 2013 Nature 497 86
Google Scholar
[22] Olmschenk S, Matsukevich D N, Maunz P 2009 Science 323 486
Google Scholar
[23] Pan J W, Bouwmeester D, Weinfurter H 1998 Phys. Rev. Lett. 80 3891
Google Scholar
[24] Bravyi S, Cross A W, Gambetta J M 2024 Nature 627 778
Google Scholar
[25] Bersin E, Sutula M, Huan Y Q 2024 PRX Quantum 5 010303
Google Scholar
[26] Fan R, Bao Y, Altman E 2024 PRX Quantum 5 020343
Google Scholar
[27] Zhang Q, Lai H, Pieprzyk J 2022 Phys. Rev. A 105 032439
Google Scholar
[28] Lai H, Pieprzyk J, Pan L 2023 Sci. China Inf. Sci. 66 180510
Google Scholar
[29] Shannon C E 1949 Bell Syst. Tech. J. 28 656
Google Scholar
[30] Orús R 2014 Ann. Phys. 349 117
Google Scholar
[31] Chen L Q, Zhao M N, Yu K L 2021 Quantum Information Processing. 20 1
Google Scholar
[32] Elkouss D, Martinez J, Lancho D 2010 IEEE Information Theory Workshop on Information Theory Cairo, Egypt, October 10—13, 2010 p1
[33] Gisin N, Ribordy G, Tittel W 2002 Rev. Mod. Phys. 74 145
Google Scholar
[34] Wu X, Zhu W P, Yan J 2017 IEEE Trans. Veh. Technol. 66 8223
Google Scholar
[35] Bennett C H, Brassard G, Robert J M 1988 SIAM J. Comput. 17 210
Google Scholar
[36] Eibl M, Kiesel N, Bourennane M, et al 2004 Phys. Rev. Lett. 92 077901
Google Scholar
[37] Briegel H J, Raussendorf R 2001 Phys. Rev. Lett. 86 910
Google Scholar
[38] Affleck I, Kennedy T, Lieb E H 2004 Condensed Matter Phys. Exactly Soluble Models: Selecta Elliott H. Lieb (Berlin: Springer-Verlag) pp249-252
[39] Affleck I 1989 J. Phys. Condens. Matter 1 3047
Google Scholar
DownLoad:
Metrics
- Abstract views: 157
- PDF Downloads: 3
- Cited By: 0
