-
High order harmonic generation (HHG) is an important phenomenon when atoms or molecules interact with an intense laser field. It can be used to generate ultrashort laser source, and can also be used to investigate the atomic and molecular dynamics and obtain the electric structure information of molecules. All these require to understand in depth the mechanism of HHG. There are complicated interference effects in HHG spectra of molecules due to multiple re-collision atomic centers in the molecule. In this paper, spectra of aligned O2 molecule in linearly polarized laser field is investigated by using the Lewenstein' s model. The dependence of the spectrum on the angle θ between the nuclear axis of the molecule and the laser polarization direction is obtained. It is shown that the maximum yield of HHG occurs at θ of 45°, which is in consistence with the experimental result. In addition, it is found that there exists a minimum value in the HHG spectrum for any given value of θ. The harmonic order corresponding to the minimum increases with θ increasing. It is found that the minimum comes from the coherent superposition of contributions from two channels. One channel refers to that the ionized electron from one atomic center, subjected to the electric field of the laser, moves back to its parent atomic center and there it combines with the molecule and emits harmonics; while the other channel is that the ionized electron generated from one atomic center move back to the other atomic center to complete the combination and emission of harmonics. The angle θ-dependent phase difference between contributions from these two channels is calculated and the harmonic order corresponding to the minimum value is obtained. Finally, the reason why the yield of HHG is low for the case of the molecular axis parallel to the laser polarization direction is different from that for the case of the molecular axis perpendicular to the polarization direction. For the parallel case, the contributions to HHG from the two channels are both small so that the amplitude of their coherent superposition is small. While for the perpendicular case, the individual contribution from each channel is not small but their destructive interference leads to small yield in harmonicspectrum.
[1] Skantzakis E, Chatziathanasiou S, Carpeggiani P A, Sansone G, Nayak A, Gray D, Tzallas P, Charalambidis D, Hertz E, Faucher O 2016 Sci. Rep. 6 39295
Google Scholar
[2] Popmintchev T, Chen M C, Popmintchev D et al. 2012 Science 336 1287
Google Scholar
[3] 宋浩, 吕孝源, 朱若碧, 陈高 2019 68 184201
Google Scholar
Song H, Lv X Y, Zhu R B, Chen G 2019 Acta Phys. Sin. 68 184201
Google Scholar
[4] Alexander M K, Marcin F, Maciej P, Stoyan K S, Kyle J M B, Bartosz A G 2006 Science 312 420
Google Scholar
[5] Itatani J, Levesque J, Zeidler D, Niikura H, Pepin H, Kieffer J C, Corkum P B, Villeneuve D M 2004 Nature 432 867
Google Scholar
[6] Torres R, Kajumba N, Underwood J G, Robinson J S, Baker S, Tisch J W G, Nalda R D, Bryan W A, Velotta R, Altucci C, Turcu I C E, Marangos J P 2007 Phys. Rev. Lett. 98 203007
Google Scholar
[7] Corkum P B 1993 Phys. Rev. Lett. 71 1994
Google Scholar
[8] Zair A, Siegel T, Sukiasyan S, Risoud F, Brugnera L, Hutchison C, Diveki Z, Auguste T, Tisch J W G, Salieres P, Ivanova M Y, Marangos J P 2013 Chem. Phys. 414 184
Google Scholar
[9] Chatziathanasiou S, Liontos I, Skantzakis E, Kahaly S, Kahaly M U, Tsatrafyllis N, Faucher O, Witzel B, Papadakis N, Charalambidis D, Tzallas P 2019 Phys. Rev. A 100 061404
[10] Lein M, Hay N, Velotta R, Marangos J P, Knight P L 2002 Phys. Rev. A 66 023805
[11] Lein M, Hay N, Velotta R, Marangos J P, Knight P L 2002 Phys. Rev. Lett. 88 183903
Google Scholar
[12] Kanai T, Minemoto S, Sakai H 2005 Nature 435 470
Google Scholar
[13] Faria C F D M 2007 Phys. Rev. A 76 043407
[14] 袁仲, 郭迎春, 王兵兵 2016 65 114205
Google Scholar
Yuan Z, Guo Y C, Wang B B 2016 Acta Phys. Sin. 65 114205
Google Scholar
[15] Zhou X X, Tong X M, Zhao Z X, Lin C D 2005 Phys. Rev. A 72 033412
[16] Itatani J, Zeidler D, Levesque J, Spanner M, Villeneuve D M, Corkum P B 2005 Phys. Rev. Lett. 94 123902
Google Scholar
[17] Lewenstein M, Balcou P, Ivanov M Y, Huillier A L, Corkum P B 1994 Phys. Rev. A 49 2117
[18] Molpro A Package of Ab Initio Programs, Werner H J, Knowles P J, Lindh R, Manby F R, Schutz M, Celani P, Korona T, Rauhut G, Amos R D, Bernhardsson A, Berning A, Cooper D L, Deegan M J O, Dobbyn A J, Eckert F, Hampel C, Hetzer G, Lloyd A W, McNicholas S J, Meyer W, Mura M E, Nicklass A, Palmieri P http://www.molpro.net/ [2020-12-12]
[19] 邓华依, 周效信 2009 原子与分子 26 101
Google Scholar
Deng H Y, Zhou X X 2009 J. At. Mol. Phys. 26 101
Google Scholar
[20] 李忠元, 郭迎春, 王兵兵 2021 华东师范大学学报(自然科学版) 1 103
Google Scholar
Li Z Y, Guo Y C, Wang B B 2021 Journal of East China Normal University (Natural Sciences) 1 103
Google Scholar
[21] Cooper J W 1962 Phys. Rev. 128 681
[22] Carlson T A, Krause M O, Grimm F A, Keller P, Taylor J W 1982 J. Chem. Phys. 77 5340
Google Scholar
[23] Worner H J, Niikura H, Bertrand J B, Corkum P B, Villeneuve D M 2009 Phys. Rev. Lett. 102 103901
Google Scholar
[24] Shiner A D, Schmidt B E, Herrero C T, Corkum P B, Kieffer J C, Legare F, Villeneuve D M 2012 J. Phys. B:At. Mol. Opt. Phys. 45 074010
Google Scholar
[25] Wong M C H, Le A T, Alharbi A F, Boguslavskiy A E, Lucchese R R, Brichta J P, Lin C D, Bhardwaj V R 2013 Phys. Rev. Lett. 110 033006
Google Scholar
-
图 1 (a)准直的O2分子与光电场示意图; (b)第一类通道; (c)第二类通道
Figure 1. (a) Aligned O2 molecule and the polarizing electric field of laser; (b) the first type of path; (c) the second type of path.
图 2 O2分子基态波函数
Figure 2. Wavefunction of ground state of O2.
图 3 O2在激光偏振与核轴成不同夹角
$\theta $ 下的高次谐波谱, 每幅图中的黑色划线为第一类通道的贡献$\log |{X_1} + {X_2}{|^2}$ ; 红色点划线为第二类通道的贡献$\log |{X_3} + {X_4}{|^2}$ ; 蓝色实线为两类通道叠加的结果$\log |{X_1} + {X_2} + {X_3} + {X_4}{|^2}$ Figure 3. The HHG spectrum of O2 with different
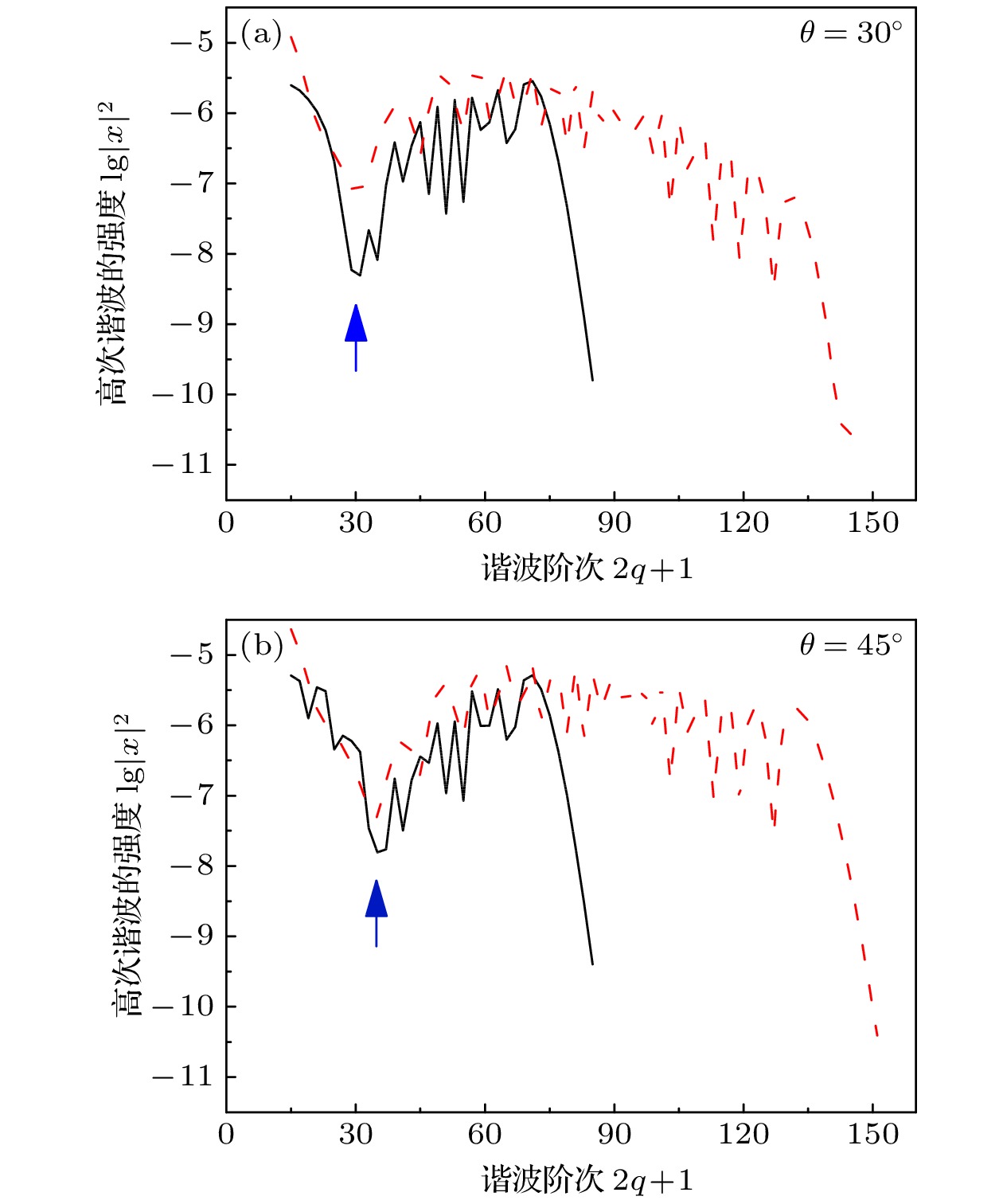
$\theta $ between the polarizing direction of laser electric field and the nuclear axis of O2: In each panel, black dash line is the contribution from the first path$\log |{X_1} + {X_2}{|^2}$ , red dot line represent that from the second path$\log |{X_3} + {X_4}{|^2}$ , and blue solid line represents the addition of the above two paths$\log |{X_1} + {X_2} + {X_3} + {X_4}{|^2}$ .
图 4 对应不同的核轴和偏振方向的夹角
$ \theta $ , 两类通道产生的高次谐波的相位差的余弦值随阶次的变化Figure 4.
$\cos (\delta \varphi )$ versus harmonic order for different angle$ \theta $ made by nuclear axis and laser polarizing direction,$\delta\varphi $ is the phase difference between HHG from two channels.
图 5 核轴和偏振方向的夹角 θ 分别为30°(图(a))和45°(图(b))时O2的高次谐波谱, 黑色实线对应的激光强度为
$5.18 \times $ $ {10^{14}}\, {{\rm{{W/c}}}}{{{{\rm{m}}}}^{{2}}}$ , 红色虚线对应$1.036 \times {10^{15}}\, {{\rm{{W/c}}}}{{{\rm{{m}}}}^{{2}}}$ Figure 5. The HHG spectrum of O2 with different
$ \theta $ between the polarizing direction of laser electric field and the nuclear axis of O2 , in panel (a)$ \theta $ is 30° and in (b)$ \theta $ is 45°. In each panel, black solid line is for the laser intensity of$5.18 \times {10^{14}}\, {{\rm{{W/c}}}}{{{\rm{{m}}}}^{{2}}}$ and short dash line is for the laser intensity of$1.036 \times {10^{15}}\, {{\rm{{W/c}}}}{{{\rm{{m}}}}^{{2}}}$ -
[1] Skantzakis E, Chatziathanasiou S, Carpeggiani P A, Sansone G, Nayak A, Gray D, Tzallas P, Charalambidis D, Hertz E, Faucher O 2016 Sci. Rep. 6 39295
Google Scholar
[2] Popmintchev T, Chen M C, Popmintchev D et al. 2012 Science 336 1287
Google Scholar
[3] 宋浩, 吕孝源, 朱若碧, 陈高 2019 68 184201
Google Scholar
Song H, Lv X Y, Zhu R B, Chen G 2019 Acta Phys. Sin. 68 184201
Google Scholar
[4] Alexander M K, Marcin F, Maciej P, Stoyan K S, Kyle J M B, Bartosz A G 2006 Science 312 420
Google Scholar
[5] Itatani J, Levesque J, Zeidler D, Niikura H, Pepin H, Kieffer J C, Corkum P B, Villeneuve D M 2004 Nature 432 867
Google Scholar
[6] Torres R, Kajumba N, Underwood J G, Robinson J S, Baker S, Tisch J W G, Nalda R D, Bryan W A, Velotta R, Altucci C, Turcu I C E, Marangos J P 2007 Phys. Rev. Lett. 98 203007
Google Scholar
[7] Corkum P B 1993 Phys. Rev. Lett. 71 1994
Google Scholar
[8] Zair A, Siegel T, Sukiasyan S, Risoud F, Brugnera L, Hutchison C, Diveki Z, Auguste T, Tisch J W G, Salieres P, Ivanova M Y, Marangos J P 2013 Chem. Phys. 414 184
Google Scholar
[9] Chatziathanasiou S, Liontos I, Skantzakis E, Kahaly S, Kahaly M U, Tsatrafyllis N, Faucher O, Witzel B, Papadakis N, Charalambidis D, Tzallas P 2019 Phys. Rev. A 100 061404
[10] Lein M, Hay N, Velotta R, Marangos J P, Knight P L 2002 Phys. Rev. A 66 023805
[11] Lein M, Hay N, Velotta R, Marangos J P, Knight P L 2002 Phys. Rev. Lett. 88 183903
Google Scholar
[12] Kanai T, Minemoto S, Sakai H 2005 Nature 435 470
Google Scholar
[13] Faria C F D M 2007 Phys. Rev. A 76 043407
[14] 袁仲, 郭迎春, 王兵兵 2016 65 114205
Google Scholar
Yuan Z, Guo Y C, Wang B B 2016 Acta Phys. Sin. 65 114205
Google Scholar
[15] Zhou X X, Tong X M, Zhao Z X, Lin C D 2005 Phys. Rev. A 72 033412
[16] Itatani J, Zeidler D, Levesque J, Spanner M, Villeneuve D M, Corkum P B 2005 Phys. Rev. Lett. 94 123902
Google Scholar
[17] Lewenstein M, Balcou P, Ivanov M Y, Huillier A L, Corkum P B 1994 Phys. Rev. A 49 2117
[18] Molpro A Package of Ab Initio Programs, Werner H J, Knowles P J, Lindh R, Manby F R, Schutz M, Celani P, Korona T, Rauhut G, Amos R D, Bernhardsson A, Berning A, Cooper D L, Deegan M J O, Dobbyn A J, Eckert F, Hampel C, Hetzer G, Lloyd A W, McNicholas S J, Meyer W, Mura M E, Nicklass A, Palmieri P http://www.molpro.net/ [2020-12-12]
[19] 邓华依, 周效信 2009 原子与分子 26 101
Google Scholar
Deng H Y, Zhou X X 2009 J. At. Mol. Phys. 26 101
Google Scholar
[20] 李忠元, 郭迎春, 王兵兵 2021 华东师范大学学报(自然科学版) 1 103
Google Scholar
Li Z Y, Guo Y C, Wang B B 2021 Journal of East China Normal University (Natural Sciences) 1 103
Google Scholar
[21] Cooper J W 1962 Phys. Rev. 128 681
[22] Carlson T A, Krause M O, Grimm F A, Keller P, Taylor J W 1982 J. Chem. Phys. 77 5340
Google Scholar
[23] Worner H J, Niikura H, Bertrand J B, Corkum P B, Villeneuve D M 2009 Phys. Rev. Lett. 102 103901
Google Scholar
[24] Shiner A D, Schmidt B E, Herrero C T, Corkum P B, Kieffer J C, Legare F, Villeneuve D M 2012 J. Phys. B:At. Mol. Opt. Phys. 45 074010
Google Scholar
[25] Wong M C H, Le A T, Alharbi A F, Boguslavskiy A E, Lucchese R R, Brichta J P, Lin C D, Bhardwaj V R 2013 Phys. Rev. Lett. 110 033006
Google Scholar
-
[1] Zhang Chun-Yan. High-order harmonic platform extension and cluster expansion of H ion cluster. Acta Physica Sinica, 2023, 72(21): 214203. doi: 10.7498/aps.72.20230534 [2] Shen Kai-Bo, Liu Ying-Guang, Li Xin, Li Heng-Xuan. Phonon interference effects in graphene nanomesh. Acta Physica Sinica, 2023, 72(12): 123102. doi: 10.7498/aps.72.20230361 [3] Yu Shu-Juan, Liu Zhu-Qin, Li Yan-Peng. Ellipticity properties of symmetric molecules $ {\text{H}}_{\text{2}}^ + $ in strong and short-wavelength laser fields. Acta Physica Sinica, 2023, 72(4): 043101. doi: 10.7498/aps.72.20221946[4] Cheng Tong, Yang Tian-Yue, Gong Ting, Guo Gu-Qing, Qiu Xuan-Bing, Li Chuan-Liang, Zhao Gang, Ma Wei-Guang. Interference suppression method in optical feedback-cavity enhanced absorption spectroscopy technology. Acta Physica Sinica, 2022, 71(6): 064205. doi: 10.7498/aps.71.20211882 [5] Yang Yan, Zhang Bin, Ren Zhong-Xue, Bai Guang-Ru, Liu Lu, Zhao Zeng-Xiu. Asymmetry in high-order harmonic generation of polar molecule CO. Acta Physica Sinica, 2022, 71(23): 234204. doi: 10.7498/aps.71.20221714 [6] Yao Hui-Dong, Cui Bo, Ma Si-Qi, Yu Chao, Lu Rui-Feng. Enhancing high harmonic generation in bilayer MoS2 by interlayer atomic dislocation. Acta Physica Sinica, 2021, 70(13): 134207. doi: 10.7498/aps.70.20210731 [7] Fan Xin, Liang Hong-Jing, Shan Li-Yu, Yan Bo, Gao Qing-Hua, Ma Ri, Ding Da-Jun. Extreme ultraviolet polarization vortex beam based on high harmonic generation. Acta Physica Sinica, 2020, 69(4): 044203. doi: 10.7498/aps.69.20190834 [8] Guan Zhong, Li Wei, Wang Guo-Li, Zhou Xiao-Xin. Study of high-order harmonic generation in crystals exposed to laser fields. Acta Physica Sinica, 2016, 65(6): 063201. doi: 10.7498/aps.65.063201 [9] Luo Xiang-Yi, Liu Hai-Feng, Ben Shuai, Liu Xue-Shen. Enhancement of high-order harmonic generation from H2+ in near plasmon-enhanced laser field. Acta Physica Sinica, 2016, 65(12): 123201. doi: 10.7498/aps.65.123201 [10] Li Gui-Hua, Xie Hong-Qiang, Yao Jin-Ping, Chu Wei, Cheng Ya, Liu Xiao-Jun, Chen Jing, Xie Xin-Hua. Signature of multi-channel interference in high-order harmonic generation from N2 driven by intense mid-infrared pulses. Acta Physica Sinica, 2016, 65(22): 224208. doi: 10.7498/aps.65.224208 [11] Yu Chao, Sun Zhen-Rong, Guo Dong-Sheng. Guo-Åberg-Crasemann theory for high harmonic generation and its cutoff law. Acta Physica Sinica, 2015, 64(12): 124207. doi: 10.7498/aps.64.124207 [12] Li Yan-Peng, Yu Shu-Juan, Chen Yan-Jun. Wavelength-dependent perpendicular-harmonics efficiency from oriented CO2 molecule. Acta Physica Sinica, 2015, 64(18): 183102. doi: 10.7498/aps.64.183102 [13] Chen Gao, Yang Yu-Jun, Guo Fu-Ming. Analysis on the cutoff frequency of high order harmonic generation in the crystal. Acta Physica Sinica, 2013, 62(8): 083202. doi: 10.7498/aps.62.083202 [14] Li Xiao-Gang, Li Fang, He Zhi-Cong. Quantum path interferences of high-order harmonic generation in two-color Gaussian beams. Acta Physica Sinica, 2013, 62(8): 087201. doi: 10.7498/aps.62.087201 [15] Guo Fu-Ming, Chen Ji-Gen, Yang Yu-Jun, Zeng Si-Liang. Mass shift effect on relativistic high-order harmonic generation. Acta Physica Sinica, 2012, 61(17): 173202. doi: 10.7498/aps.61.173202 [16] Cui Lei, Wang Xiao-Juan, Wang Fan, Zeng Xiang-Hua. Effect of laser polarization direction on high order harmonic generation of oxygen molecule——A simulation via TDDFT. Acta Physica Sinica, 2010, 59(1): 317-321. doi: 10.7498/aps.59.317 [17] Li Hui-Shan, Li Peng-Cheng, Zhou Xiao-Xin. Role of potential function in high order harmonic generation of model hydrogen atoms in intense laser field. Acta Physica Sinica, 2009, 58(11): 7633-7639. doi: 10.7498/aps.58.7633 [18] Gu Bin, Cui Lei, Zeng Xiang-Hua, Zhang Feng-Shou. High-order harmonic generation of hydrogen molecule irradiated by ultra-strong femto-second laser pulse——a simulation via TDDFT. Acta Physica Sinica, 2006, 55(6): 2972-2976. doi: 10.7498/aps.55.2972 [19] Cui Lei, Gu Bin, Teng Yu-Yong, Hu Yong-Jin, Zhao Jiang, Zeng Xiang-Hua. Effect of different laser polarization direction on high order harmonic generation of nitrogen molecule——A simulation via TDDFT. Acta Physica Sinica, 2006, 55(9): 4691-4694. doi: 10.7498/aps.55.4691 [20] Wang Da-Wei, Liu Ting-Ting, Yang Hong, Jiang Hong-Bin, Gong Qi-Huang. . Acta Physica Sinica, 2002, 51(9): 2034-2037. doi: 10.7498/aps.51.2034
DownLoad:
Catalog
Metrics
- Abstract views: 4523
- PDF Downloads: 68
- Cited By: 0
