High-order harmonic platform extension and cluster expansion of H ion cluster

Zhang Chun-Yan

doi:10.7498/aps.72.20230534

Abstract

By solving the time-dependent Schrödinger equation for the interaction of the intense laser field with the two-dimensional model of H ion cluster, it is found that the high-order harmonic plateau produced by H ion cluster is wider than that generated by a single H atom. The interaction between intense laser field and cluster is decomposed into three processes: internal ionization, classical motion under the action of external field and Coulomb field of the cluster ions, and recombination. After internal ionization, the particle is deemed classical and its motion follows Newton’s equation of motion. By studying the classical trajectory of electron and the variation of kinetic and potential energy with time, it is observed that during the electron’s returning, the additional kinetic energy is required as a result of the reduction in potential energy. Furthermore, the correlation between return energy and return time obtained from the classical model is in good agreement with that obtained from time-dependent Schrödinger equation. In this study, the cutoff energy of high-order harmonic generated by clusters is compared with that of a single atom, indicating that the extension of the platform of high-order harmonic by clusters is primarily caused by the Coulomb effect of other ions surrounding the parent nucleus. Additionally, the influence of ion spacing on the cutoff energy of high-order harmonic is also investigated, and a possible relationship between the cut-off energy of high harmonic and the cluster expansion is established.

Keywords:

Authors and contacts

Zhang Chun-Yan^1,2

1.
College of Physics and Information Technology, Shaanxi Normal University, Xi’an 710119, China
2.
School of Intelligence Science and Engineering, Hubei Minzu University, Enshi 445000, China

Corresponding author: Zhang Chun-Yan, 2012004@hbmzu.edu.cn

FullText HTML : translate this paragraph

References

[1]	Itatani J, Levesque J, Zeidler D, Niikura H, Pépin H, Kieffer J C, Corkum P B, Villeneuve D M 2004 Nature 432 867 Google Scholar
[2]	祝晓松, 张庆斌, 兰鹏飞, 陆培祥 2016 65 224207 Google Scholar Zhu X S, Zhang Q B, Lan P F, Lu P X 2016 Acta Phys. Sin. 65 224207 Google Scholar
[3]	Yu S J, Li W Y, Li Y P, Chen Y J 2017 Phys. Rev. A 96 013432 Google Scholar
[4]	Su N, Yu S J, Li W Y, Yang S P, Chen Y J 2018 Chin. Phys. B 27 054213 Google Scholar
[5]	Qiao Y, Huo Y Q, Liang H Q, Chen J G, Liu, W J, Yang Y J, Jiang S C 2022 Opt. Express 30 9971 Google Scholar
[6]	Qiao Y, Huo Y Q, Jiang S C, Yang Y J, Chen J G 2023 Phys. Rev. B 107 075201 Google Scholar
[7]	陶琛玉, 雷建廷, 余璇, 骆炎, 马新文, 张少锋 2023 72 053202 Google Scholar Tao C Y, Lei J T, Yu X, Luo Y, Ma X W, Zhang S F 2023 Acta Phys. Sin. 72 053202 Google Scholar
[8]	Papadogiannis N A, Witzel B, Kalpouzos C, Charalambidis D 1999 Phys. Rev. Lett. 83 4289 Google Scholar
[9]	Hentschel M, Kienberger R, Spielmann C, Reider G A, Milosevic N, Brabec T, Corkum P, Heinzmann U, Drescher M, Krausz F 2001 Nature 414 509 Google Scholar
[10]	Goulielmakis E, Uiberacker M, Kienberger R, Baltuska A, Yakovlev V, Scrinzi A, Westerwalbesloh T, Kleineberg U, Heinzmann U, Drescher M, Krausz F 2004 Science 305 1267 Google Scholar
[11]	Sandberg R L, Paul A, Raymondson D A, Haedrich S, Gaudiosi D M, Holtsnider J, Tobey R I, Cohen O, Murnane M M, Kapteyn H C, Song C, Miao J, Liu Y, Salmassi F 2007 Phys. Rev. Lett. 99 098103 Google Scholar
[12]	Iii C D, Rundquist A R, Murnane M M, Kapteyn H C 1998 Science 280 1412 Google Scholar
[13]	Corkum P B 1993 Phys. Rev. Lett. 71 1994 Google Scholar
[14]	Yang Y J, Chen G, Chen J G, Zhu Q R 2004 Chin. Phys. Lett. 21 652 Google Scholar
[15]	Yang Y J, Chen J G, Chi F P, Zhu Q R, Zhang H X, Sun J Z 2007 Chin. Phys. Lett. 24 1537 Google Scholar
[16]	成春芝, 周效信, 李鹏程 2011 60 202 Google Scholar Cheng C Z, Zhou X X, Li P C 2011 Acta Phys. Sin. 60 202 Google Scholar
[17]	Artemyev A N, Cederbaum L S , Demekhin P V 2017 Phys. Rev. A 95 033402
[18]	刘艳, 郭福明, 杨玉军 2019 68 173202 Google Scholar Liu Y, Guo F M, Yang Y J 2019 Acta Phys. Sin. 68 173202 Google Scholar
[19]	Zhou X, Lock R, Wagner N, Li W, Kapteyn H C, Murnane M M 2009 Phys. Rev. Lett. 102 073902 Google Scholar
[20]	于术娟, 刘竹琴, 李雁鹏 2023 72 043101 Google Scholar Yu S J, Liu Z Q, Li Y P 2023 Acta Phys. Sin. 72 043101 Google Scholar
[21]	Ghimire S, Ndabashimiye G, DiChiara A D, Sistrunk E, Stockman M I, Agostini P, DiMauro L F, Reis D A 2014 J. Phys. B: At. Mol. Opt. Phys. 47 204030 Google Scholar
[22]	Vampa G, McDonald C R, Orlando G, Corkum P B, Brabec T 2015 Phys. Rev. B 91 064302 Google Scholar
[23]	Kruchinin S Yu, Krausz F, Yakovlev V S 2018 Rev. Mod. Phys. 90 021002 Google Scholar
[24]	Li L, Zhang Y F, Lan P F, Huang T F, Zhu X S, Zhai C Y, Yang K, He L X, Zhang Q B, Cao W, Lu P X 2021 Phys. Rev. Lett. 126 187401 Google Scholar
[25]	Qiao Y, Chen J Q, Huo Y Q, Liang H Q, Yu R X, Chen J G, Liu W J, Jiang S C, Yang Y J 2023 Phys. Rev. A 107 023523 Google Scholar
[26]	Véniard V, Taïeb R, Maquet A 1999 Phys. Rev. A 60 3952 Google Scholar
[27]	Vozzi C, Nisoli M, Caumes J P, Sansone G, Stagira S, Silvestri S D 2005 Appl. Phys. Lett. 86 111121 Google Scholar
[28]	Hu S X, Xu Z Z 1997 Appl. Phys. Lett. 71 2605 Google Scholar
[29]	Tisch J W G , Ditmire T, Fraser D J, Hay N, Mason M B , Springate E, Marangos J P, Hutchinson M H R 1997 J. Phys. B: At. Mol. Opt. Phys. 30 L709 Google Scholar
[30]	Aladi M, Márton I, Rácz P, Dombi P, Földes I B 2014 High Power Laser Sci. Eng. 2 E32 Google Scholar
[31]	Donnelly T D, Ditmire T, Neumann K, Perry M D, Falcone R W 1996 Phys. Rev. Lett. 76 2472 Google Scholar
[32]	Feng L, Liu H 2015 Phys. Plasmas 22 013107 Google Scholar
[33]	Numico R, Giulietti D, Giulietti A, Gizzi L A, Roso L 2000 J. Phys. B: At. Mol. Opt. Phys. 33 2605 Google Scholar
[34]	Vázquez de Aldana J R, Roso L 2001 J. Opt. Soc. Am. B 18 325 Google Scholar
[35]	Park H, Wang Z, Xiong H, Schoun S B, Xu J, Agostini P, DiMauro L F 2014 Phys. Rev. Lett. 113 263401 Google Scholar
[36]	Tao Y, Hagmeijer R, Bastiaens H M J, Goh S J, van der Slot P J M, Biedron S G, Milton S V, Boller K J 2017 New J. Phys. 19 083017 Google Scholar
[37]	Ruf H, Handschin C, Cireasa R, Thiré N, Ferré A, Petit S, Descamps D, Mével E, Constant E, Blanchet V, Fabre B, Mairesse Y 2013 Phys. Rev. Lett. 110 083902 Google Scholar
[38]	Moreno P, Plaja L, Roso L 1994 Europhys. Lett. 28 629 Google Scholar
[39]	Zaretsky D F, Korneev P, Becker W 2010 J. Phys. B: At. Mol. Opt. Phys. 43 105402 Google Scholar
[40]	Bodi B, Aladi M, Racz P, Foldes I B, Dombi P 2019 Opt. Express 27 26721 Google Scholar
[41]	Véniard V, Taïeb R, Maquet A 2001 Phys. Rev. A 65 013202 Google Scholar
[42]	Li N N, Zhai Z, Liu X S 2008 Chin. Phys. Lett. 25 2508 Google Scholar
[43]	Strelkov V, Saalmann U, Becker A, Rost J M 2011 Phys. Rev. Lett. 107 113901 Google Scholar
[44]	Feit M D, Jr Fleck J A, Steiger A 1982 J. Comput. Phys. 47 412 Google Scholar
[45]	Saalmann U, Rost J M 2008 Phys. Rev. Lett. 100 133006 Google Scholar

Cited By

图 1 二维模型团簇结构示意图　(a) H⁸⁺结构示意图; (b) H²⁴⁺结构示意图

Figure 1. Schematic diagram of cluster structure of two-dimensional model: (a) Structure diagram of H⁸⁺; (b) structure diagram of H²⁴⁺.

DownLoad: Full-Size Img PowerPoint

图 2 团簇的势能曲面　(a) H⁸⁺势能曲面; (b) H²⁴⁺势能曲面.

Figure 2. Potential energy surface of cluster: (a) The potential energy surface of H⁸⁺; (b) the potential energy surface of H²⁴⁺.

DownLoad: Full-Size Img PowerPoint

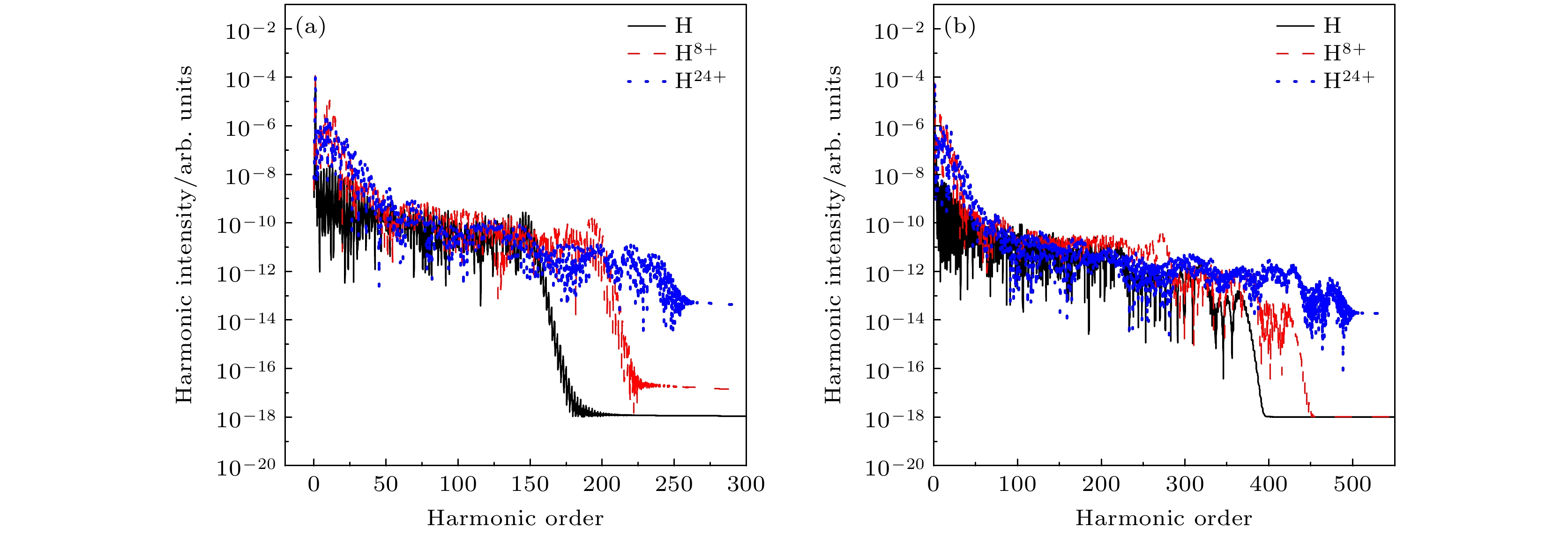
图 3 强激光场与H原子和H团簇相互作用产生的高次谐波(谐波阶表示谐波发射频率$ \omega $与激光基频$ {\omega _0} $的比值)　(a) I = 3×10¹⁴ W/cm², λ = 1200 nm; (b) I = 5×10¹⁴ W/cm², λ = 1400 nm

Figure 3. High order harmonic generated from the interaction between intense laser field and H atom/H cluster: (a) I = 3×10¹⁴ W/cm² , λ = 1200 nm; (b) I = 5×10¹⁴ W/cm², λ = 1400 nm.

DownLoad: Full-Size Img PowerPoint

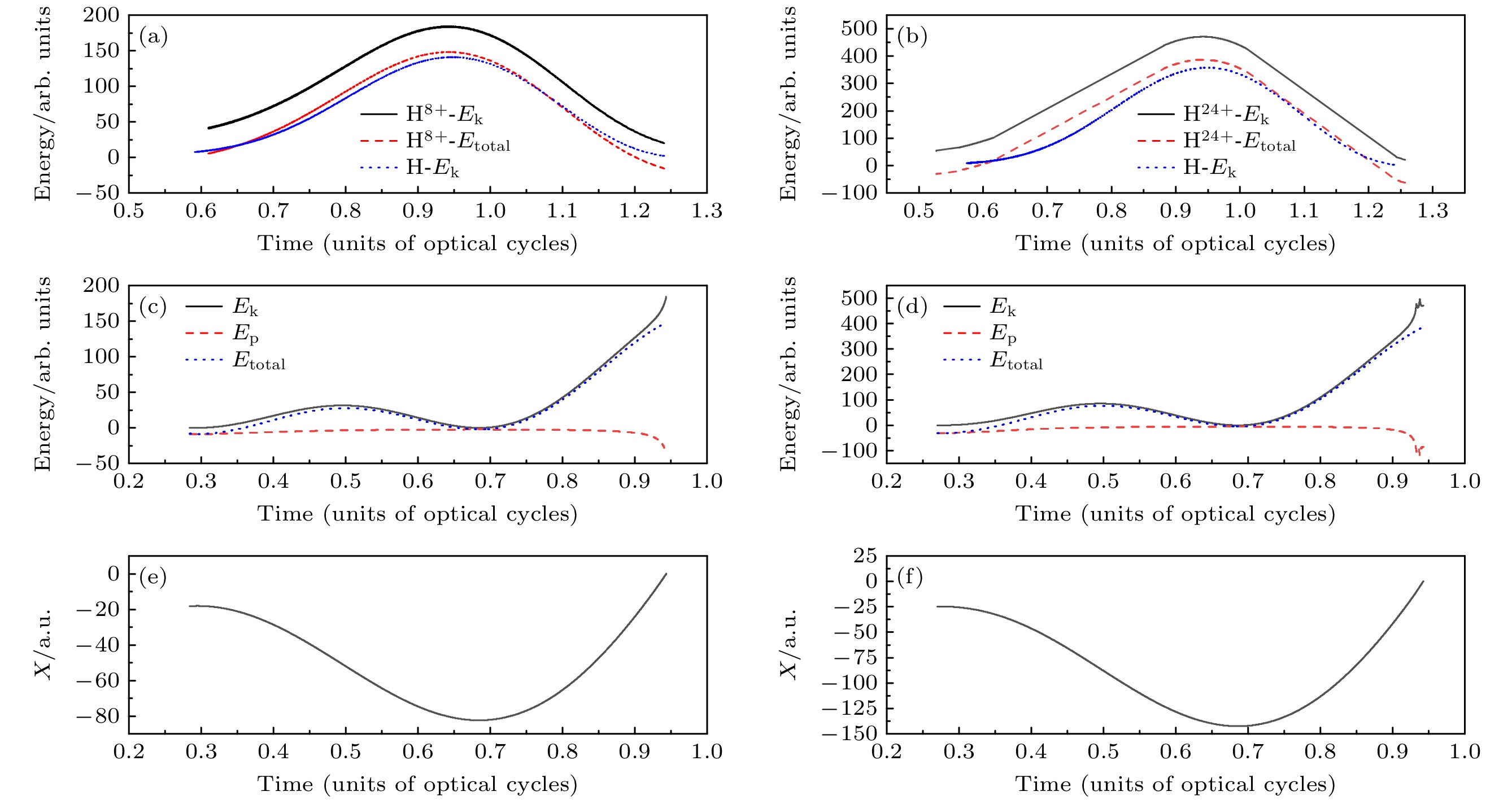
图 4 (a), (c), (e) I = 3×10¹⁴ W/cm² , λ = 1200 nm的线偏振激光与H⁸⁺团簇相互作用时的电子动力学行为; (b), (d), (f) I = 5×10¹⁴ W/cm², λ = 1400 nm的线偏振激光与H²⁴⁺团簇相互作用时的电子动力学行为. (a), (b) 电子返回时间与返回能量的关系, 其中黑色实线表示动能、红色划线表示总能量、蓝色点线表示相应参数激光场与H原子相互作用时电子的返回动能与返回时间的关系; (c), (d) 电子的动能、势能及总能量随时间的变化, 其中黑色实线表示动能、红色划线表示势能、蓝色点线表示总能量; (e), (f)电子在X轴方向上位移随时间的变化

Figure 4. Electron dynamic behavior of linearly polarized laser interacting with cluster: (a), (c), (e) For H⁸⁺ cluster illuminated by the laser with I = 3×10¹⁴ W/cm² , λ = 1200 nm; (b), (d), (f) for H²⁴⁺ cluster illuminated by the laser with I = 5×10¹⁴ W/cm², λ = 1400 nm. (a), (b) The relation between the return time and the return energy of the electron, where the black solid line represents the kinetic energy, the red dash line represents the total energy, and the blue dot line represents the kinetic energy from H atom; (c), (d) the energy change over time, where the black solid line represents kinetic energy, the red dash line represents potential energy, and the blue dot line represents total energy; (e), (f) displacement variations with time along X direction.

DownLoad: Full-Size Img PowerPoint

图 5 图4(d)和图4(f)的部分放大图

Figure 5. Partial enlargement of Fig. 4(d)and Fig. 4(f).

DownLoad: Full-Size Img PowerPoint

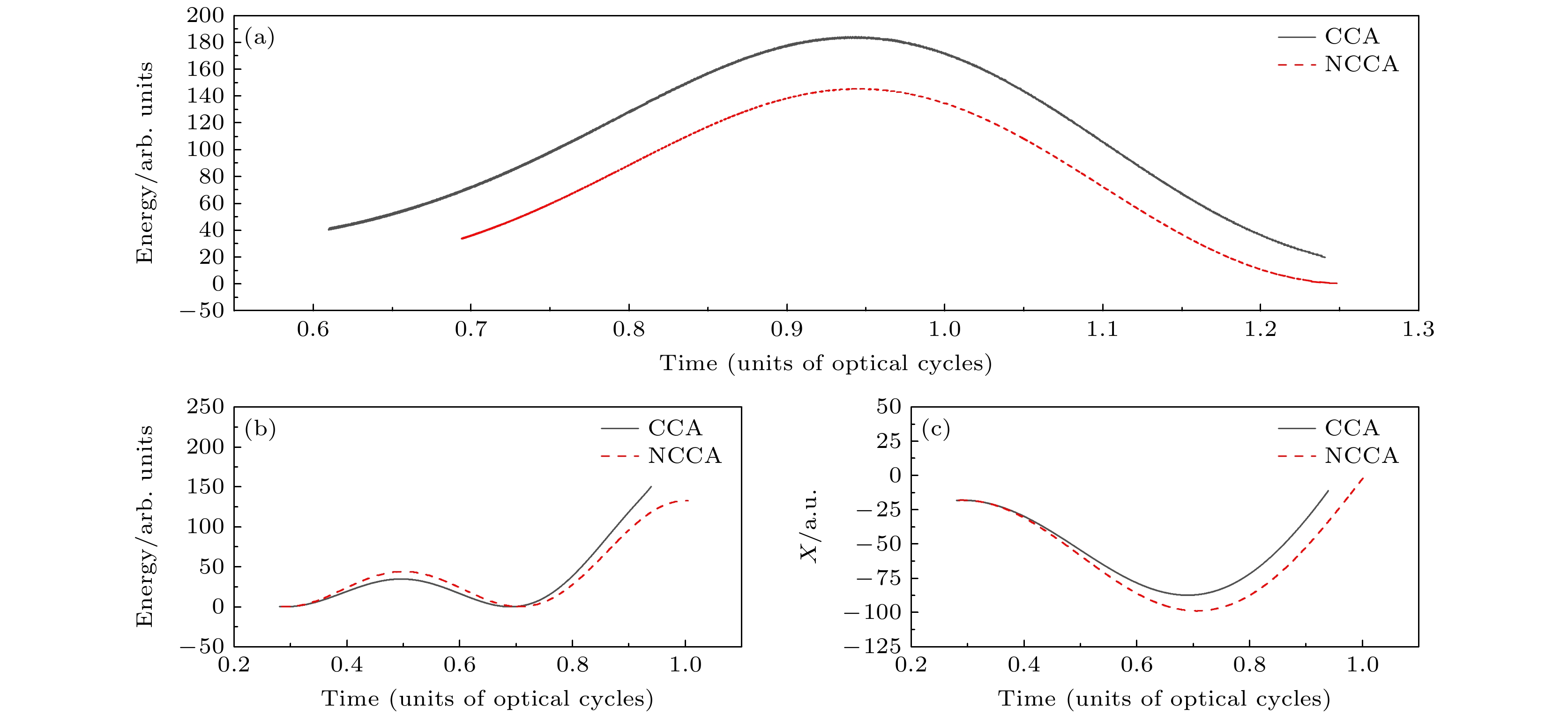
图 6 I = 3×10¹⁴ W/cm², λ = 1200 nm的线偏振激光与H⁸⁺团簇相互作用过程中考虑(CCA)和不考虑库仑势(NCCA)影响的情况下电子的动力学行为　(a)电子返回时间与返回动能的关系; (b) 电子的动能随时间变化情况; (c)电子在X轴方向上位移随时间的变化

Figure 6. Dynamical behavior of the electron with and without the influence of the Coulomb potential for H⁸⁺ cluster illuminated by the laser with I = 3×10¹⁴ W/cm², λ = 1200 nm: (a) The relationship between electron return time and return kinetic energy; (b) the variation of the kinetic energy of electrons over time; (c) the displacement of electrons in the X-axis direction over time.

DownLoad: Full-Size Img PowerPoint

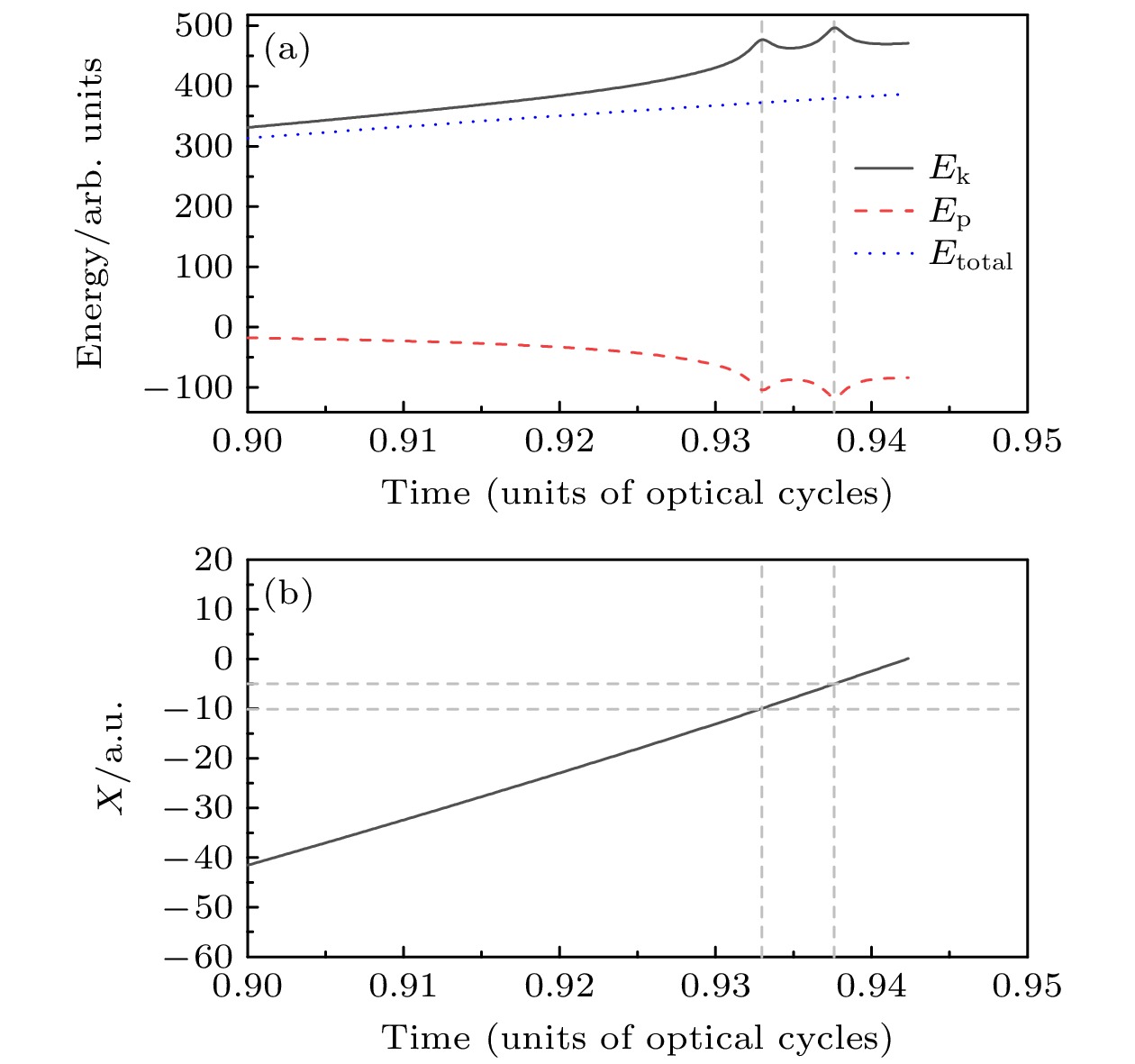
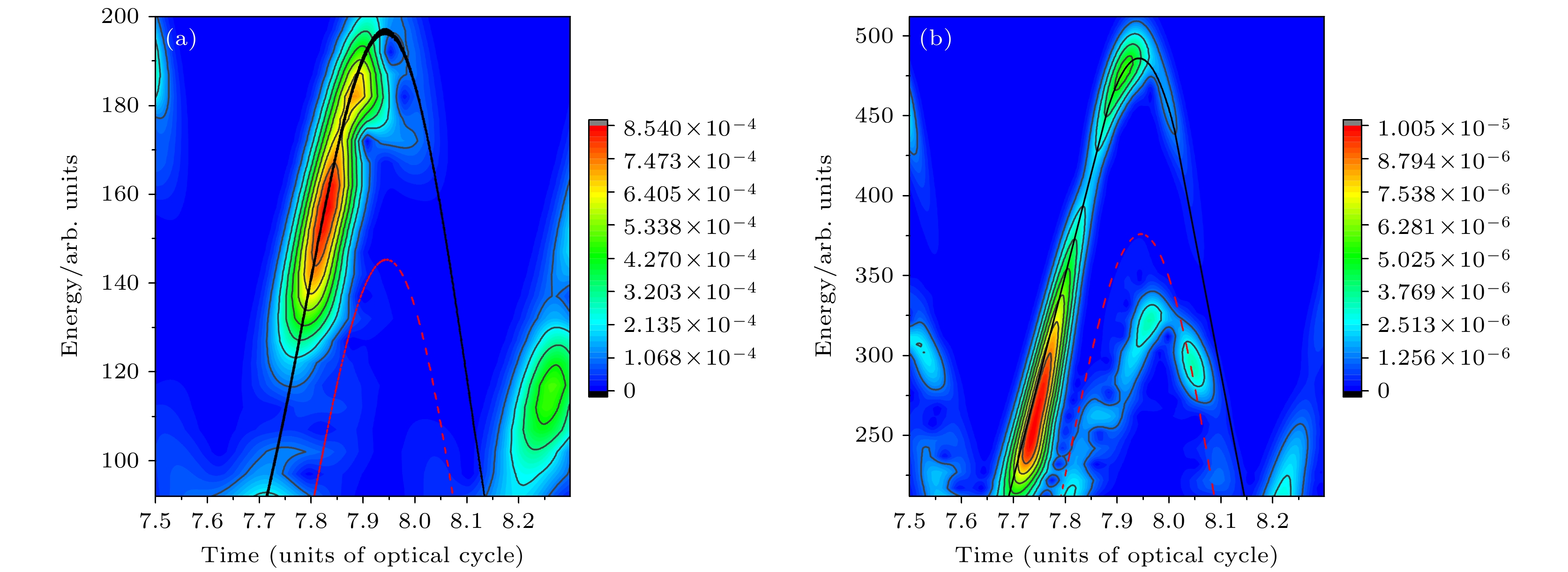
图 7 通过TDSE计算得到的高次谐波时频分布图(图中黑色实线表示考虑库仑作用时通过经典计算得到的返回动能与单个原子的电离能之和与返回时间的关系, 红色划线表示不考虑库仑作用时电子返回时间与返回动能的关系)　(a) I = 3×10¹⁴ W/cm², λ = 1200 nm的线偏振激光与H⁸⁺团簇相互作用; (b) I = 5×10¹⁴ W/cm², λ = 1400 nm的线偏振激光与H²⁴⁺团簇相互作用

Figure 7. Time-frequency distribution of higher harmonics calculated by TDSE: (a) H⁸⁺ cluster illuminated by the laser with I = 3×10¹⁴ W/cm², λ = 1200 nm; (b) H²⁴⁺ cluster illuminated by the laser with I = 5×10¹⁴ W/cm², λ = 1400 nm. The black solid line represents the relationship between the sum of the ionization energy of a single atom and return kinetic energy obtained by classical calculation and the return time in the case of considering Coulomb effect, while the red dash line represents the relation between the return time and the return energy of the electron in the case of no considering Coulomb effect.

DownLoad: Full-Size Img PowerPoint

图 8 (a) I = 3×10¹⁴ W/cm², λ = 1200 nm的线偏振激光与离子间距不同的H⁸⁺团簇相互作用时产生的高次谐波; (b)通过经典计算得到的返回动能与单个原子的电离能之和与返回时间的关系

Figure 8. (a) High-order harmonics generate from the interaction between the linearly polarized laser and H^{8 +} cluster with different ion spacing, where I = 3×10¹⁴ W/cm², λ = 1200 nm; (b) the relationship between the sum of the ionization energy of a single atom and return kinetic energy obtained by classical calculation and the return time.

DownLoad: Full-Size Img PowerPoint

map

[1]	Itatani J, Levesque J, Zeidler D, Niikura H, Pépin H, Kieffer J C, Corkum P B, Villeneuve D M 2004 Nature 432 867 Google Scholar
[2]	祝晓松, 张庆斌, 兰鹏飞, 陆培祥 2016 65 224207 Google Scholar Zhu X S, Zhang Q B, Lan P F, Lu P X 2016 Acta Phys. Sin. 65 224207 Google Scholar
[3]	Yu S J, Li W Y, Li Y P, Chen Y J 2017 Phys. Rev. A 96 013432 Google Scholar
[4]	Su N, Yu S J, Li W Y, Yang S P, Chen Y J 2018 Chin. Phys. B 27 054213 Google Scholar
[5]	Qiao Y, Huo Y Q, Liang H Q, Chen J G, Liu, W J, Yang Y J, Jiang S C 2022 Opt. Express 30 9971 Google Scholar
[6]	Qiao Y, Huo Y Q, Jiang S C, Yang Y J, Chen J G 2023 Phys. Rev. B 107 075201 Google Scholar
[7]	陶琛玉, 雷建廷, 余璇, 骆炎, 马新文, 张少锋 2023 72 053202 Google Scholar Tao C Y, Lei J T, Yu X, Luo Y, Ma X W, Zhang S F 2023 Acta Phys. Sin. 72 053202 Google Scholar
[8]	Papadogiannis N A, Witzel B, Kalpouzos C, Charalambidis D 1999 Phys. Rev. Lett. 83 4289 Google Scholar
[9]	Hentschel M, Kienberger R, Spielmann C, Reider G A, Milosevic N, Brabec T, Corkum P, Heinzmann U, Drescher M, Krausz F 2001 Nature 414 509 Google Scholar
[10]	Goulielmakis E, Uiberacker M, Kienberger R, Baltuska A, Yakovlev V, Scrinzi A, Westerwalbesloh T, Kleineberg U, Heinzmann U, Drescher M, Krausz F 2004 Science 305 1267 Google Scholar
[11]	Sandberg R L, Paul A, Raymondson D A, Haedrich S, Gaudiosi D M, Holtsnider J, Tobey R I, Cohen O, Murnane M M, Kapteyn H C, Song C, Miao J, Liu Y, Salmassi F 2007 Phys. Rev. Lett. 99 098103 Google Scholar
[12]	Iii C D, Rundquist A R, Murnane M M, Kapteyn H C 1998 Science 280 1412 Google Scholar
[13]	Corkum P B 1993 Phys. Rev. Lett. 71 1994 Google Scholar
[14]	Yang Y J, Chen G, Chen J G, Zhu Q R 2004 Chin. Phys. Lett. 21 652 Google Scholar
[15]	Yang Y J, Chen J G, Chi F P, Zhu Q R, Zhang H X, Sun J Z 2007 Chin. Phys. Lett. 24 1537 Google Scholar
[16]	成春芝, 周效信, 李鹏程 2011 60 202 Google Scholar Cheng C Z, Zhou X X, Li P C 2011 Acta Phys. Sin. 60 202 Google Scholar
[17]	Artemyev A N, Cederbaum L S , Demekhin P V 2017 Phys. Rev. A 95 033402
[18]	刘艳, 郭福明, 杨玉军 2019 68 173202 Google Scholar Liu Y, Guo F M, Yang Y J 2019 Acta Phys. Sin. 68 173202 Google Scholar
[19]	Zhou X, Lock R, Wagner N, Li W, Kapteyn H C, Murnane M M 2009 Phys. Rev. Lett. 102 073902 Google Scholar
[20]	于术娟, 刘竹琴, 李雁鹏 2023 72 043101 Google Scholar Yu S J, Liu Z Q, Li Y P 2023 Acta Phys. Sin. 72 043101 Google Scholar
[21]	Ghimire S, Ndabashimiye G, DiChiara A D, Sistrunk E, Stockman M I, Agostini P, DiMauro L F, Reis D A 2014 J. Phys. B: At. Mol. Opt. Phys. 47 204030 Google Scholar
[22]	Vampa G, McDonald C R, Orlando G, Corkum P B, Brabec T 2015 Phys. Rev. B 91 064302 Google Scholar
[23]	Kruchinin S Yu, Krausz F, Yakovlev V S 2018 Rev. Mod. Phys. 90 021002 Google Scholar
[24]	Li L, Zhang Y F, Lan P F, Huang T F, Zhu X S, Zhai C Y, Yang K, He L X, Zhang Q B, Cao W, Lu P X 2021 Phys. Rev. Lett. 126 187401 Google Scholar
[25]	Qiao Y, Chen J Q, Huo Y Q, Liang H Q, Yu R X, Chen J G, Liu W J, Jiang S C, Yang Y J 2023 Phys. Rev. A 107 023523 Google Scholar
[26]	Véniard V, Taïeb R, Maquet A 1999 Phys. Rev. A 60 3952 Google Scholar
[27]	Vozzi C, Nisoli M, Caumes J P, Sansone G, Stagira S, Silvestri S D 2005 Appl. Phys. Lett. 86 111121 Google Scholar
[28]	Hu S X, Xu Z Z 1997 Appl. Phys. Lett. 71 2605 Google Scholar
[29]	Tisch J W G , Ditmire T, Fraser D J, Hay N, Mason M B , Springate E, Marangos J P, Hutchinson M H R 1997 J. Phys. B: At. Mol. Opt. Phys. 30 L709 Google Scholar
[30]	Aladi M, Márton I, Rácz P, Dombi P, Földes I B 2014 High Power Laser Sci. Eng. 2 E32 Google Scholar
[31]	Donnelly T D, Ditmire T, Neumann K, Perry M D, Falcone R W 1996 Phys. Rev. Lett. 76 2472 Google Scholar
[32]	Feng L, Liu H 2015 Phys. Plasmas 22 013107 Google Scholar
[33]	Numico R, Giulietti D, Giulietti A, Gizzi L A, Roso L 2000 J. Phys. B: At. Mol. Opt. Phys. 33 2605 Google Scholar
[34]	Vázquez de Aldana J R, Roso L 2001 J. Opt. Soc. Am. B 18 325 Google Scholar
[35]	Park H, Wang Z, Xiong H, Schoun S B, Xu J, Agostini P, DiMauro L F 2014 Phys. Rev. Lett. 113 263401 Google Scholar
[36]	Tao Y, Hagmeijer R, Bastiaens H M J, Goh S J, van der Slot P J M, Biedron S G, Milton S V, Boller K J 2017 New J. Phys. 19 083017 Google Scholar
[37]	Ruf H, Handschin C, Cireasa R, Thiré N, Ferré A, Petit S, Descamps D, Mével E, Constant E, Blanchet V, Fabre B, Mairesse Y 2013 Phys. Rev. Lett. 110 083902 Google Scholar
[38]	Moreno P, Plaja L, Roso L 1994 Europhys. Lett. 28 629 Google Scholar
[39]	Zaretsky D F, Korneev P, Becker W 2010 J. Phys. B: At. Mol. Opt. Phys. 43 105402 Google Scholar
[40]	Bodi B, Aladi M, Racz P, Foldes I B, Dombi P 2019 Opt. Express 27 26721 Google Scholar
[41]	Véniard V, Taïeb R, Maquet A 2001 Phys. Rev. A 65 013202 Google Scholar
[42]	Li N N, Zhai Z, Liu X S 2008 Chin. Phys. Lett. 25 2508 Google Scholar
[43]	Strelkov V, Saalmann U, Becker A, Rost J M 2011 Phys. Rev. Lett. 107 113901 Google Scholar
[44]	Feit M D, Jr Fleck J A, Steiger A 1982 J. Comput. Phys. 47 412 Google Scholar
[45]	Saalmann U, Rost J M 2008 Phys. Rev. Lett. 100 133006 Google Scholar

[1]	Zhang Hai-Song, Lu Mao-Cong, Li Zhi-Gang. An expansion effect based pseudo-boiling critical point model for supercritical CO₂. Acta Physica Sinica, 2024, 73(18): 184402. doi: 10.7498/aps.73.20240293
[2]	Yao Hui-Dong, Cui Bo, Ma Si-Qi, Yu Chao, Lu Rui-Feng. Enhancing high harmonic generation in bilayer MoS₂ by interlayer atomic dislocation. Acta Physica Sinica, 2021, 70(13): 134207. doi: 10.7498/aps.70.20210731
[3]	Fan Xin, Liang Hong-Jing, Shan Li-Yu, Yan Bo, Gao Qing-Hua, Ma Ri, Ding Da-Jun. Extreme ultraviolet polarization vortex beam based on high harmonic generation. Acta Physica Sinica, 2020, 69(4): 044203. doi: 10.7498/aps.69.20190834
[4]	Cai Huai-Peng^1\2, Gao Jian^1\2, Li Bo-Yuan^1\2, Liu Feng^1\2, Chen Li-Ming^1\2\3, Yuan Xiao-Hui^1\2, Chen Min^1\2, Sheng Zheng-Ming^1\2\4\5, Zhang Jie^1\2\3. High order harmonics generation by relativistically circularly polarized laser-solid interaction. Acta Physica Sinica, 2018, 67(21): 214205. doi: 10.7498/aps.67.20181574
[5]	Li Xia-Zhi, Zou De-Bin, Zhou Hong-Yu, Zhang Shi-Jie, Zhao Na, Yu De-Yao, Zhuo Hong-Bin. Effect of plasma grating roughness on high-order harmonic generation. Acta Physica Sinica, 2017, 66(24): 244209. doi: 10.7498/aps.66.244209
[6]	Luo Xiang-Yi, Liu Hai-Feng, Ben Shuai, Liu Xue-Shen. Enhancement of high-order harmonic generation from H2+ in near plasmon-enhanced laser field. Acta Physica Sinica, 2016, 65(12): 123201. doi: 10.7498/aps.65.123201
[7]	Wang Hua, Chen Qiong, Wang Wen-Guang, Hou Mei-Ying. Experimental study of clustering behaviors in granular gases. Acta Physica Sinica, 2016, 65(1): 014502. doi: 10.7498/aps.65.014502
[8]	Guan Zhong, Li Wei, Wang Guo-Li, Zhou Xiao-Xin. Study of high-order harmonic generation in crystals exposed to laser fields. Acta Physica Sinica, 2016, 65(6): 063201. doi: 10.7498/aps.65.063201
[9]	Yu Chao, Sun Zhen-Rong, Guo Dong-Sheng. Guo-Åberg-Crasemann theory for high harmonic generation and its cutoff law. Acta Physica Sinica, 2015, 64(12): 124207. doi: 10.7498/aps.64.124207
[10]	Chen Gao, Yang Yu-Jun, Guo Fu-Ming. Analysis on the cutoff frequency of high order harmonic generation in the crystal. Acta Physica Sinica, 2013, 62(8): 083202. doi: 10.7498/aps.62.083202
[11]	Han Xiao-Jing, Wang Yin, Lin Zheng-Zhe, Zhang Wen-Xian, Zhuang Jun, Ning Xi-Jing. Theoretical prediction of the growth probabilities for cluster isomers. Acta Physica Sinica, 2010, 59(5): 3445-3449. doi: 10.7498/aps.59.3445
[12]	E Xiao-Liang, Duan Hai-Ming. Study of the structure evolution and ground state energy of ConCu55－n(n=0—55) bimetallic clusters by using the Gupta potential combined with a genetic algorithm. Acta Physica Sinica, 2010, 59(8): 5672-5680. doi: 10.7498/aps.59.5672
[13]	Li Hui-Shan, Li Peng-Cheng, Zhou Xiao-Xin. Role of potential function in high order harmonic generation of model hydrogen atoms in intense laser field. Acta Physica Sinica, 2009, 58(11): 7633-7639. doi: 10.7498/aps.58.7633
[14]	Yang Ming, Liu Jian-Sheng, Cai Yi, Wang Wen-Tao, Wang Cheng, Ni Guo-Quan, Li Ru-Xin, Xu Zhi-Zhan. Diagnosis and investigation of the formation of low density and large sized clusters. Acta Physica Sinica, 2008, 57(1): 176-180. doi: 10.7498/aps.57.176
[15]	Wang Li, Zhang Xiao-An, Yang Zhi-Hu, Chen Xi-Meng, Zhang Hong-Qiang, Cui Ying, Shao Jian-Xiong, Xu Xu. The coulomb potential energy effect on the intensity of the characteristic lines at highly charged ion incendence on Al surface. Acta Physica Sinica, 2008, 57(1): 137-142. doi: 10.7498/aps.57.137
[16]	Yuan Yong-Bo, Liu Yu-Zhen, Deng Kai-Ming, Yang Jin-Long. Assignment of photoelectron spectra of SiN cluster. Acta Physica Sinica, 2006, 55(9): 4496-4500. doi: 10.7498/aps.55.4496
[17]	Zhang Qiu-Ju, Sheng Zheng-Ming, Zhang Jie. Redshift of harmonics by laser interaction with solid target. Acta Physica Sinica, 2004, 53(7): 2180-2183. doi: 10.7498/aps.53.2180
[18]	Li Peng-Cheng, Zhou Xiao-Xin, Dong Chen-Zhong, Zhao Song-Feng. Investigation of the high harmonic generation and ionization of atoms with long-range and short-range potentials in intense laser fields. Acta Physica Sinica, 2004, 53(3): 750-755. doi: 10.7498/aps.53.750
[19]	Wang Da-Wei, Liu Ting-Ting, Yang Hong, Jiang Hong-Bin, Gong Qi-Huang. . Acta Physica Sinica, 2002, 51(9): 2034-2037. doi: 10.7498/aps.51.2034
[20]	YU SHENG, LI HONG-FU, XIE ZHONG-LIAN, LUO YONG. A NONLINEAR SIMULATION ON BEAM-WAVE INTERACTION FOR HIGH-HARMONIC COMPLEX CAVITY GYROTRON WITH RADUAL TRANSITION. Acta Physica Sinica, 2000, 49(12): 2455-2459. doi: 10.7498/aps.49.2455

Catalog

Vol. 72, Issue 21 - 2023-11-05

Metrics

Abstract views: 1795
PDF Downloads: 47
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板