-
通过数值计算, 研究了强短波(
$ 400—600{\text{ nm}} $ )激光场中${\text{H}}_2^+$ 分子高次谐波辐射的椭偏率性质. 研究表明,${\text{H}}_2^+$ 分子在不同激光强度、不同激光波长、不同核间距及不同取向角下高次谐波的椭偏率性质是不同的; 特别是在两中心干涉区, 激发态在高次谐波产生中起着重要作用, 但在不同取向角下, 激发态对谐波椭偏率的影响不同; 分析表明, 这些不同的影响源于沿平行和垂直于激光偏振方向辐射的高次谐波的相对产量, 以及激发态对平行和垂直谐波产量的影响; 此外, 椭偏率的测量检验了强场近似和平面波近似在强短波激光场中是成立的, 并对强短波激光场中分子动力学做了更充分的研究.Ellipticity properties of high-order harmonic generation (HHG) from symmetric molecules$ {\text{H}}_{\text{2}}^ + $ in strong and short wavelength (less than 800nm) laser fields are numerically investigated. In this study, the ellipticity of harmonic is compared with the corresponding harmonic spectrum and dipole, and the calculation results are analyzed and the results obtained at different laser intensities, different laser wavelengths, different internuclear distances and different orientation angles are compared with each other. Our numerical simulations show that the influences of laser intensity, laser wavelength, internuclear distance and orientation angle on the ellipticity of harmonic are different. Especially in a two-center interference region, the excited state plays an important role in the HHG, but the effects of the excited state on the ellipticity of harmonic are different at different orientation angles. Further analysis shows that these different effects are due to the influence of the excited state on the harmonic yield. Using the numerical scheme, it is determined that in the two-center interference region, the excited state plays an important role in the parallel harmonic spectrum, while the effects of the excited state on the perpendicular harmonics at different angles are all very small, which results in different phase differences between the accurate harmonic spectrum and the harmonic spectrum only returning to the ground state. Overall, the relative yields of the accurate perpendicular harmonics are lower (higher) than those of the accurate parallel harmonics, but the intensities of the perpendicular harmonics, which only return to the ground state, are comparable to (or farther away from) those of the parallel harmonics which are only to return to ground state in the two-center interference regions. Therefore, the small (large) intensity ratio between the accurate perpendicular harmonic and accurate parallel harmonic can be attributed to the contributions of the excited state to harmonics. Then we can conclude that the harmonic spectra that only go back to the ground state show high (small) ellipticity, whereas the accurate harmonic spectra show small (high) ellipticity, resulting in a strong angle dependence of the influence of the excited state on the ellipticity of harmonic. In addition, in the high-order harmonic plateau region, the relative yields of harmonics can be well predicted by the corresponding dipoles, indicating the applicability of tunneling pictures and plane wave approximation in the strong and short-wave laser fields. When the ellipticity of harmonic occurs in the interference region due to the two-center characteristics of the symmetric potential, the results show that the polarization measurement can also be used to detect the structures of symmetric molecules and track the dynamic behaviors of excited states.-
Keywords:
- high-order harmonic generation /
- strong and short wave laser field /
- the polarization properties of harmonics /
- dipole
[1] L’Huillier A, Schafer K J, Kulander K C 1991 J. Phys. B 24 3315
Google Scholar
[2] Itatani J, Levesque J, Zeidler Hiromichi Niikura D, Pepin H, Kieffer J C, Corkum P B, Villeneuve D M 2004 Nature 432 867
Google Scholar
[3] Krausz F, Ivanov M 2009 Rev. Mod. Phys. 81 163
Google Scholar
[4] Le V H, Le A T, Xie R H, Lin C D 2007 Phys. Rev. A 76 013414
Google Scholar
[5] Vozzi C, Negro M, Calegari F, Sansone G, Nisoli M, Silvestri S De, Stagira S 2011 Nat. Phys. 7 822
Google Scholar
[6] Smirnova O, Mairesse Y, Patchkovskii S, Dudovich N, Villeneuve D, Corkum P, Ivanov M Yu 2009 Nature 460 972
Google Scholar
[7] Shafifir D, Soifer H, Bruner B D, Dagan M, Mairesse Y, Patchkovskii S, Ivanov M Yu, Smirnova O, Dudovich N 2012 Nature 485 343
Google Scholar
[8] Corkum P B 1993 Phys. Rev. Lett. 71 1994
Google Scholar
[9] Lewenstein M, Balcou Ph, Ivanov M Yu, L'Huillier Anne, Corkum P B 1994 Phys. Rev. A 49 2117
Google Scholar
[10] Keldysh L V 1965 Sov. Phys. JETP 20 1307
[11] Kim V V, Ganeev R A, Boltaev G S, Alnaser A S 2020 J. Phys. B 53 155405
Google Scholar
[12] Dong F L, Tian Y Q, Yu S J, Wang S, Yang S P, Chen Y J 2015 Opt. Express 23 18106
Google Scholar
[13] Zhou X, Lock R, Wagner N, Li W, Kapteyn H C, Murnane M M 2009 Phys. Rev. Lett. 102 073902
Google Scholar
[14] Levesque J, Mairesse Y, Dudovich N, epin H P, Kieffer J C, Corkum P B, Villeneuve D M 2007 Phys. Rev. Lett. 99 243001
Google Scholar
[15] Ramakrishna S, Sherratt P A J, Dutoi A D, Seideman T 2010 Phys. Rev. A 81 021802(R
Google Scholar
[16] Strelkov V V, Gonoskov A A, Gonoskov I A, Ryabikin M Yu 2011 Phys. Rev. Lett. 107 043902
Google Scholar
[17] Akagi H, Otobe T, Staudte A, Shiner A, Turner F, Dörner R, Villeneuve D M, Corkum P B 2009 Science 325 1364
Google Scholar
[18] Bian X B, Bandrauk A D 2010 Phys. Rev. Lett. 105 093903
Google Scholar
[19] Chen Y J, Zhang B 2011 Phys. Rev. A 84 053402
Google Scholar
[20] Qin M, Zhu X, Zhang Q, Hong W, Lu P 2011 Opt. Express 19 25084
Google Scholar
[21] Du H, Luo L, Wang X, Hu B 2012 Phys. Rev. A 86 013846
Google Scholar
[22] Yu S J, Zhang B, Li Y P, Yang S P, Chen Y J 2014 Phys. Rev. A 90 053844
Google Scholar
[23] Barreau L, Veyrinas K, Gruson V, Weber S J, Auguste T, Hergott J F, Lepetit F, Carré B, Houver J -C, Dowek D, Salières P 2018 Nat. Commun. 9 4727
Google Scholar
[24] Sun F J, Chen C, Li W Y, Liu X, Li W, Chen Y J 2021 Phys. Rev. A 103 053108
Google Scholar
[25] Habibović D, Milošević D B 2020 Photonics 7 110
Google Scholar
[26] Huo X X, Xing Y H, Qi T, Sun Y, Li Bo, Zhang J, Liu X S 2021 Phys. Rev. A 103 053116
Google Scholar
[27] Chen Y J 2011 Phys. Rev. A 84 043423
Google Scholar
[28] Chen Y J, Zhang B 2012 Phys. Rev. A 86 023415
Google Scholar
[29] Bian X B, Bandrauk A D 2012 Phys. Rev. A 86 053417
Google Scholar
[30] Miao X Y, Zhang C P 2014 Phys. Rev. A 89 033410
Google Scholar
[31] Han Y C 2013 Phys. Rev. A 87 043404
Google Scholar
[32] Feit M D, Jr Fleck J A, Steiger A 1982 J. Comput. Phys. 47 412
Google Scholar
[33] Shiner A D, Trallero-Herrero C, Kajumba N, Bandulet H C, Comtois D, Légaré F, Giguère M, Kieffffer J C, Corkum P B, Villeneuve D M 2009 Phys. Rev. Lett. 103 073902
Google Scholar
[34] Yu S J, Li W Y, Li Y P, Chen Y J 2017 Phys. Rev. A 96 013432
Google Scholar
[35] Chen Y J, Hu B 2009 J. Chem. Phys. 131 244109
Google Scholar
[36] Chen Y J, Chen J, Liu J 2006 Phys. Rev. A 74 063405
Google Scholar
-
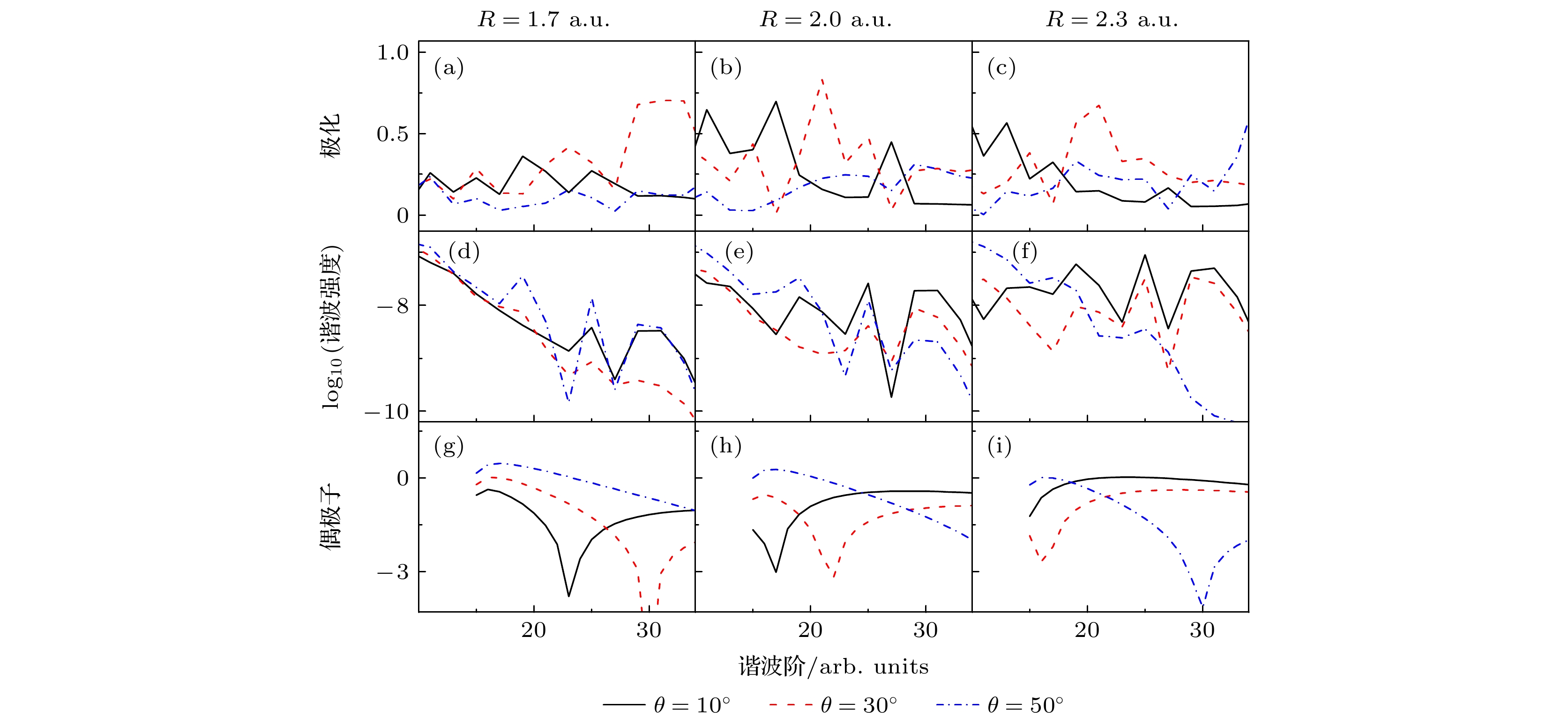
图 1
${\text{H}}_2^ + $ 分子在激光强度$ I = 4 \times {10^{14}}{\text{ W}}/{\text{c}}{{\text{m}}^2} $ 及波长$ \lambda = 600{\text{nm}} $ 时谐波的椭偏率、谐波谱及偶极子的比较 (a), (d), (g) 核间距为$ R = 1.7{\text{ a}}{\text{.u}}{\text{. }} $ ; (b), (e), (h) 核间距为$ R = 2{\text{ a}}{\text{.u}}{\text{. }} $ ; (c), (f), (i) 核间距为$ R = 2.3{\text{ a}}{\text{.u}}{\text{. }} $ Fig. 1. Comparison of the harmonic ellipticity, harmonic spectra and corresponding dipole for
${\text{H}}_2^ + $ molecules at the laser intensity$ I = 4 \times {10^{14}}{\text{ W}}/{\text{c}}{{\text{m}}^2} $ and wavelength$ \lambda = 600{\text{ nm}} $ : (a), (d), (g)$ R = 1.7{\text{ a}}. {\text{u}}. $ ; (b), (e), (h)$ R = 2{\text{ a}}. {\text{u}}. $ ; (c), (f), (i)$ R = 2.3{\text{ a}}. {\text{u}}. $ .
图 2 与图1相同, 但激光强度
$I = 5 \times {10^{14}}\;{\text{W}}/{\text{c}}{{\text{m}}^2}$ 和波长$\lambda = 400\;{\text{nm}}$ Fig. 2. Same as Fig.1, but the laser intensity
$ I = 5 \times {10^{14}}{\text{ W}}/{\text{c}}{{\text{m}}^2} $ and wavelength$ \lambda = 400{\text{ nm}} $ .
图 3 与图1相同, 但激光强度
$I = 5 \times {10^{14}}\;{\text{W}}/{\text{c}}{{\text{m}}^2}$ 和波长$\lambda = 500\;{\text{nm}}$ Fig. 3. Same as Fig.1, but the laser intensity
$I = 5 \times {10^{14}}\;{\text{W}}/{\text{c}}{{\text{m}}^2}$ and wavelength$\lambda = 500\;{\text{nm}}$ .
图 4
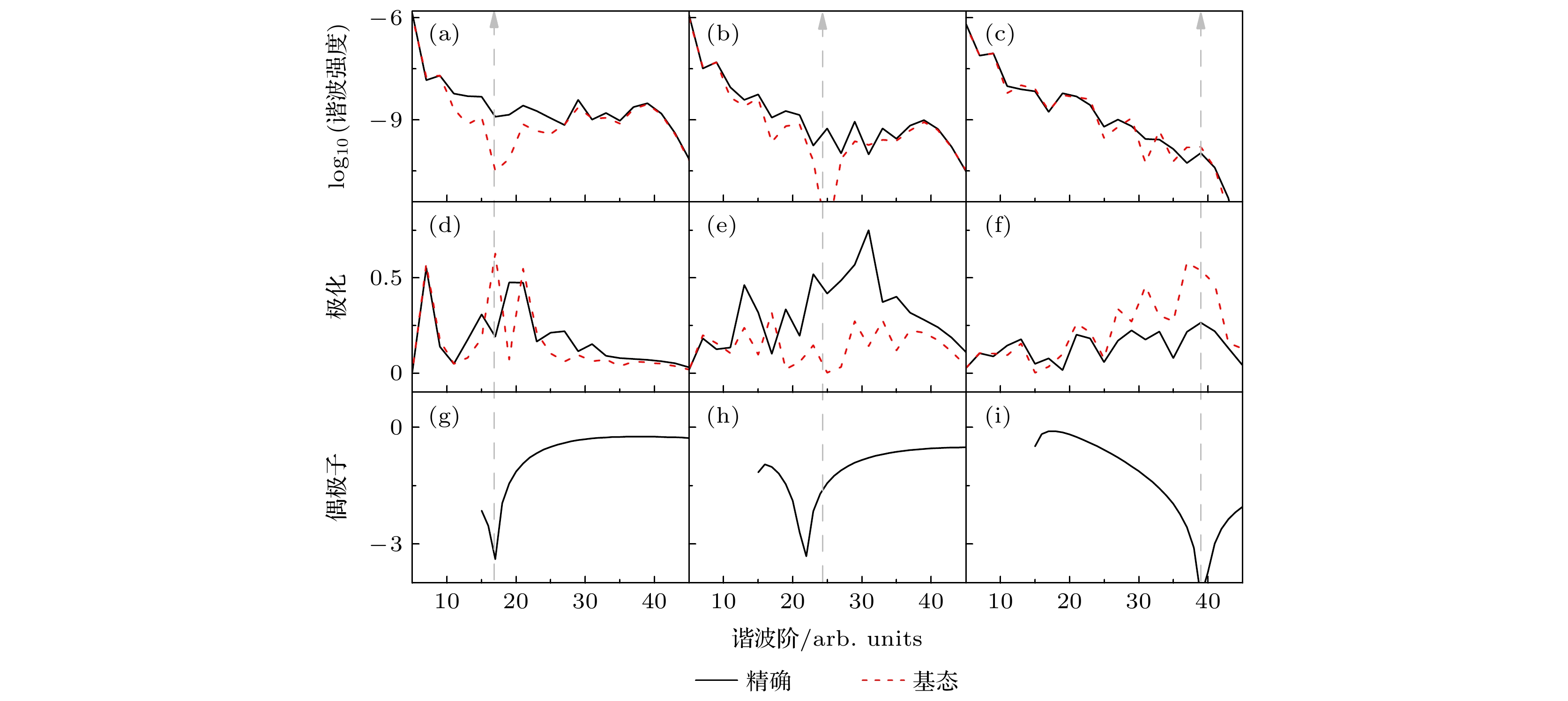
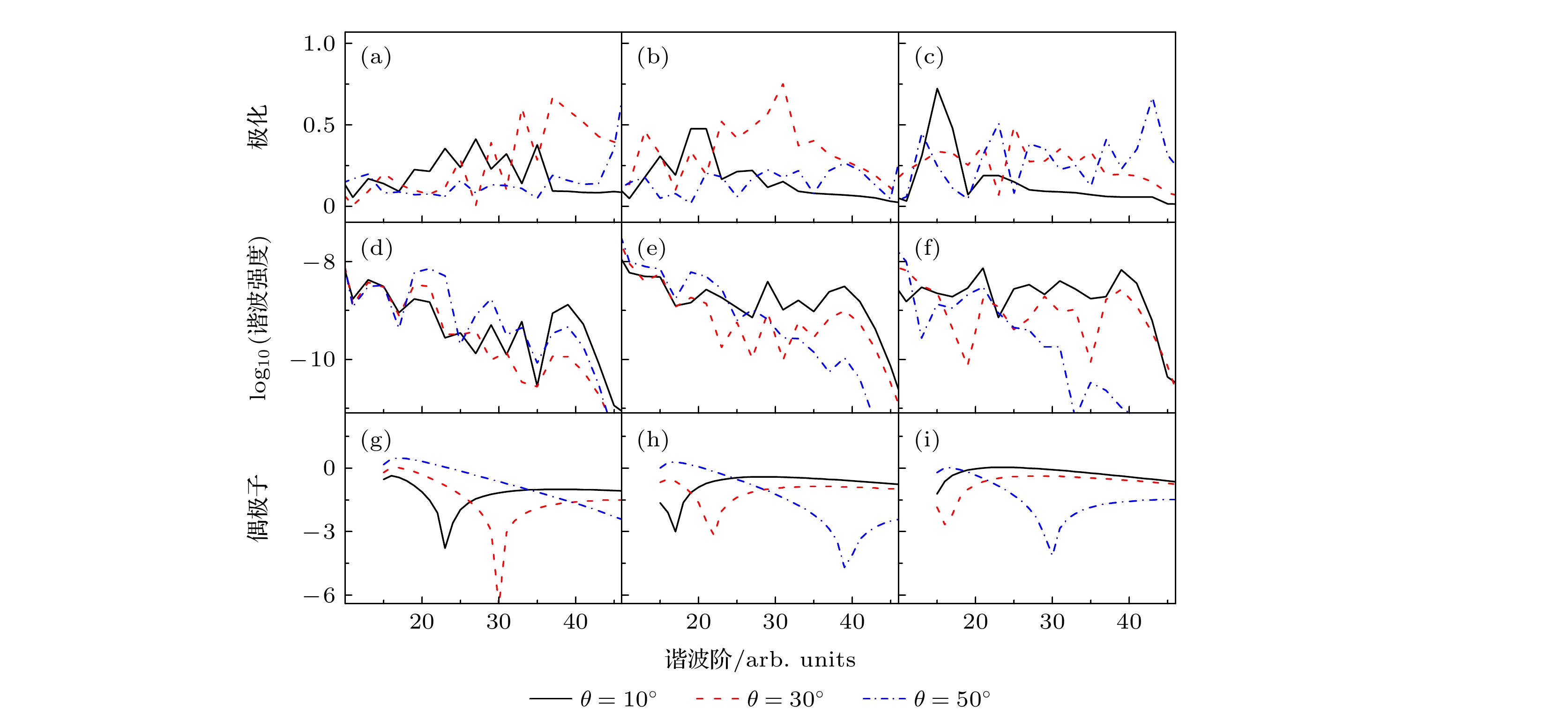
${\text{H}}_2^ + $ 分子$I = 4 \times {10^{14}}\;{\text{W}}/{\text{c}}{{\text{m}}^2}$ ,$ \lambda = 600{\text{ nm}} $ 及R=2 a.u.时谐波谱、偶极子和谐波椭偏率的比较 (a), (d), (g)$ \theta = {10^\circ} $ ; (b), (e), (h)$ \theta = {30^\circ} $ ; (c), (f), (i)$ \theta = {50^\circ} $ Fig. 4. Comparison of the harmonic ellipticity, harmonic spectra and corresponding dipole for
${\text{H}}_2^ + $ molecules with R=2 a.u. at the laser intensity$ I = 4 \times {10^{14}}{\text{ W}}/{\text{c}}{{\text{m}}^2} $ and wavelength$ \lambda = 600{\text{ nm}} $ : (a), (d), (g)$ \theta = {10^\circ} $ ; (b), (e), (h)$ \theta = {30^\circ} $ ; (c), (f), (i)$ \theta = {50^\circ} $ .
图 5
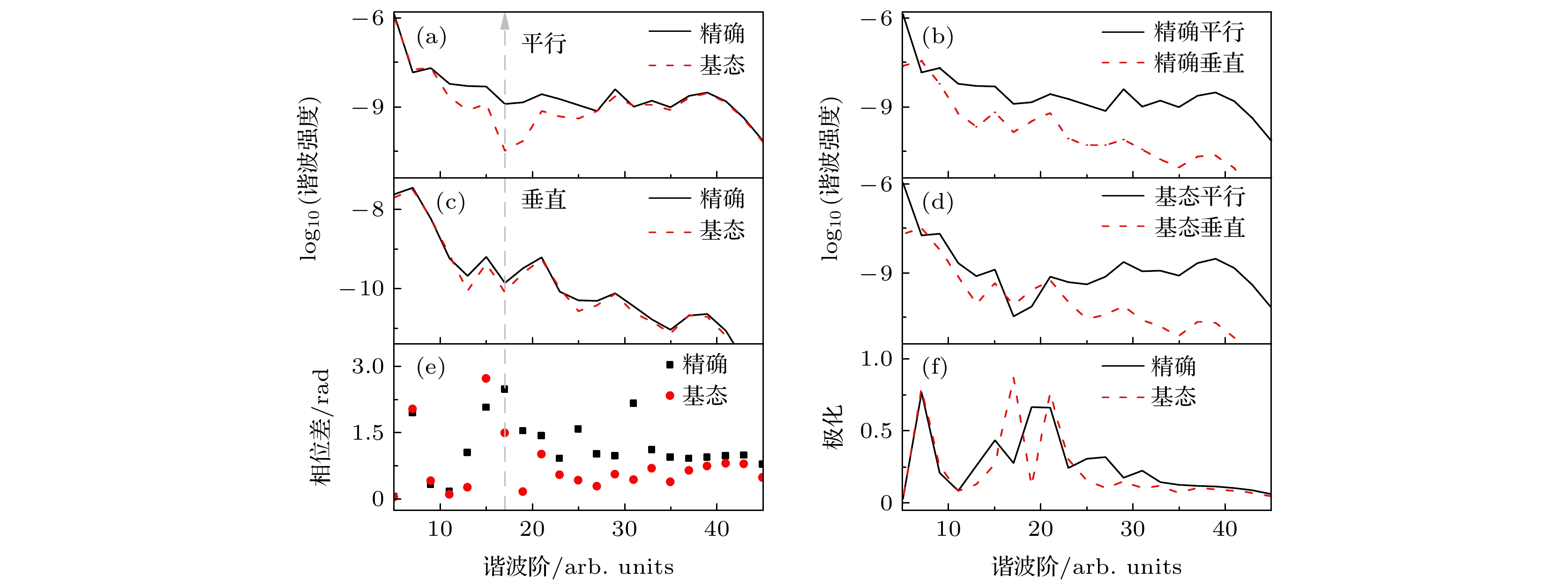
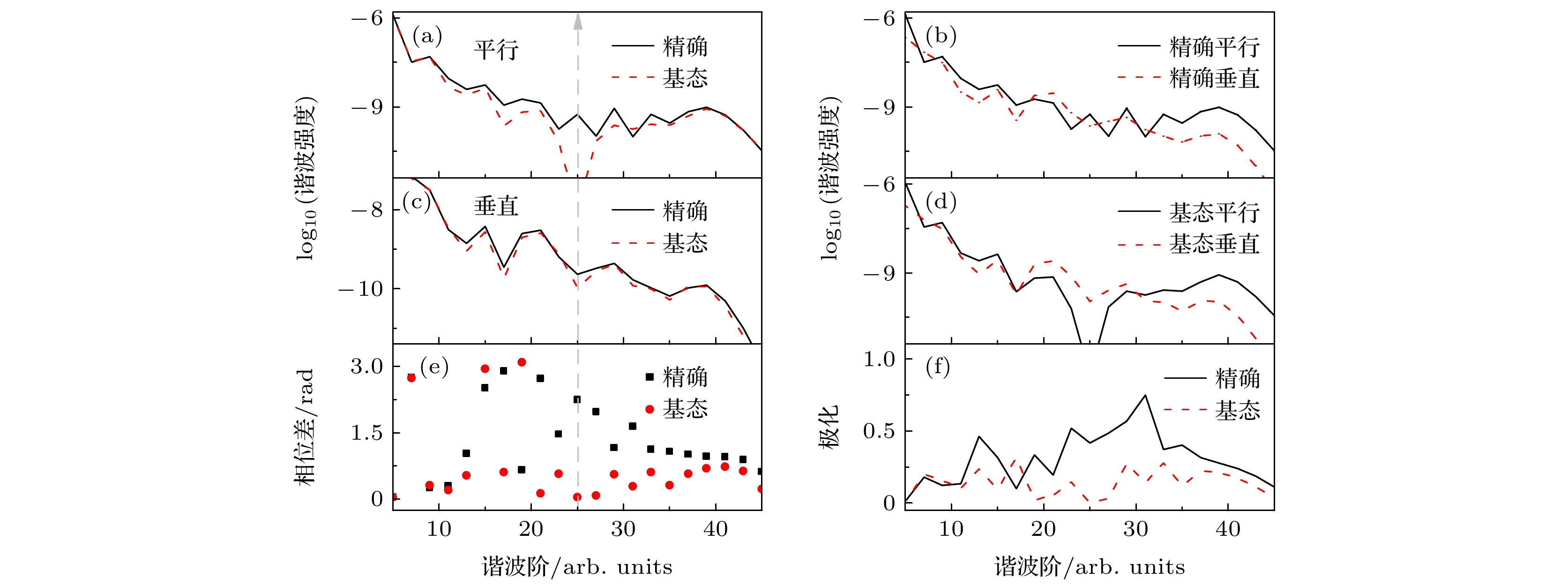
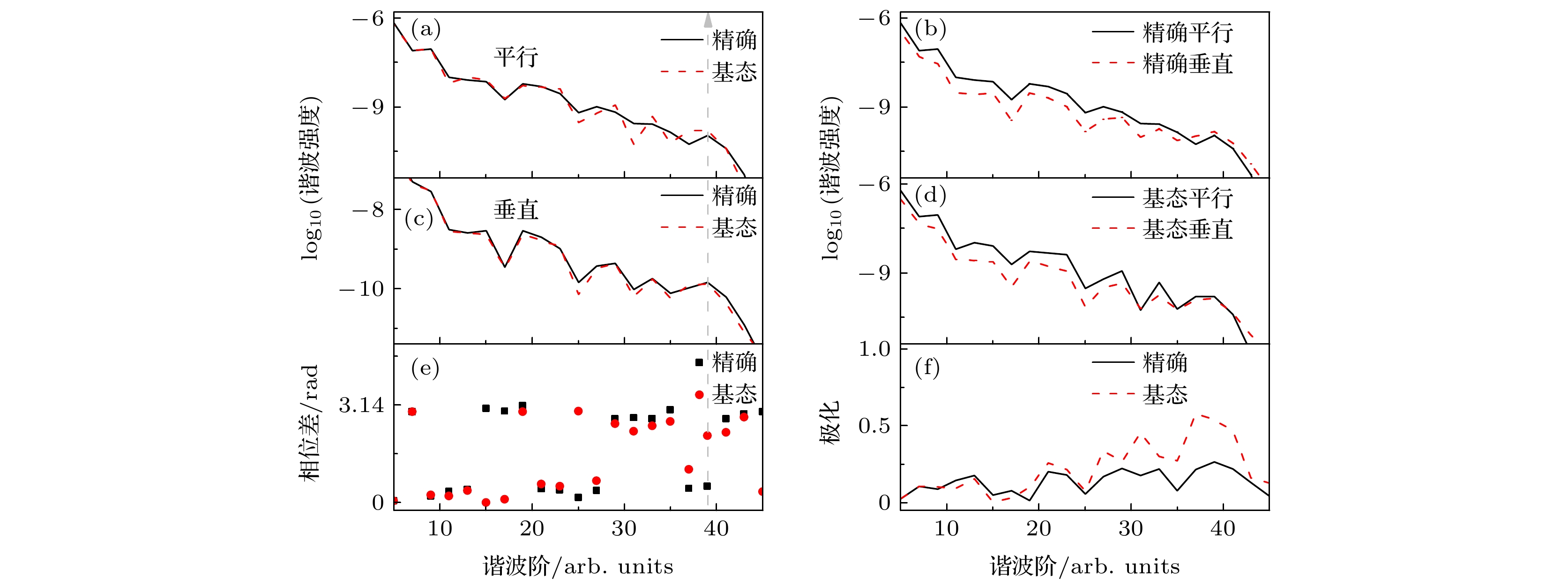
${\text{H}}_2^ + $ 分子$I = 4 \times {10^{14}}\;{\text{ W}}/{\text{c}}{{\text{m}}^2}$ ,$\lambda = 600\;{\text{nm}}$ , R=2 a.u.及$ \theta = {10^\circ} $ 时谐波谱、相位差和谐波椭偏率的比较 (a) 精确平行与跃迁回基态的平行谐波谱(基态平行谐波)比较; (b) 精确平行与精确垂直谐波谱的比较; (c) 精确与基态垂直谐波谱的比较; (d) 基态平行与基态垂直谐波谱的比较; (e) 精确与基态谐波相位差比较; (f) 精确与基态谐波椭偏率比较Fig. 5. The comparison of the harmonic spectra, the phase differences
$ {\delta _1}\left( d \right) $ and the ellipticity of harmonic for${\text{H}}_2^ + $ molecules with R=2 a.u. and$ \theta = {10^\circ} $ at the laser intensity$I = 4 \times {10^{14}}\;{\text{W}}/{\text{c}}{{\text{m}}^2}$ and wavelength$\lambda = 600\;{\text{ nm}}$ : (a) The comparison of accurate parallel harmonic and the parallel harmonic that transition back to ground state (ground-state parallel harmonic); (b) the comparison of accurate parallel and perpendicular harmonic; (c) comparison between accurate and ground state perpendicular harmonic spectrum; (d) comparison between ground-state parallel and ground-state perpendicular harmonic; (e) the comparison of the phase difference of accurate and ground-state harmonic; (f) comparison between accurate and ground-state harmonic ellipticity.
图 6 与图5相同, 但
$ \theta = {30^\circ} $ Fig. 6. Same as Fig. 5, but
$ \theta = {30^\circ} $ .
图 7 与图5相同, 但
$ \theta = {50^\circ} $ Fig. 7. Same as Fig.5, but
$ \theta = {50^\circ} $ . -
[1] L’Huillier A, Schafer K J, Kulander K C 1991 J. Phys. B 24 3315
Google Scholar
[2] Itatani J, Levesque J, Zeidler Hiromichi Niikura D, Pepin H, Kieffer J C, Corkum P B, Villeneuve D M 2004 Nature 432 867
Google Scholar
[3] Krausz F, Ivanov M 2009 Rev. Mod. Phys. 81 163
Google Scholar
[4] Le V H, Le A T, Xie R H, Lin C D 2007 Phys. Rev. A 76 013414
Google Scholar
[5] Vozzi C, Negro M, Calegari F, Sansone G, Nisoli M, Silvestri S De, Stagira S 2011 Nat. Phys. 7 822
Google Scholar
[6] Smirnova O, Mairesse Y, Patchkovskii S, Dudovich N, Villeneuve D, Corkum P, Ivanov M Yu 2009 Nature 460 972
Google Scholar
[7] Shafifir D, Soifer H, Bruner B D, Dagan M, Mairesse Y, Patchkovskii S, Ivanov M Yu, Smirnova O, Dudovich N 2012 Nature 485 343
Google Scholar
[8] Corkum P B 1993 Phys. Rev. Lett. 71 1994
Google Scholar
[9] Lewenstein M, Balcou Ph, Ivanov M Yu, L'Huillier Anne, Corkum P B 1994 Phys. Rev. A 49 2117
Google Scholar
[10] Keldysh L V 1965 Sov. Phys. JETP 20 1307
[11] Kim V V, Ganeev R A, Boltaev G S, Alnaser A S 2020 J. Phys. B 53 155405
Google Scholar
[12] Dong F L, Tian Y Q, Yu S J, Wang S, Yang S P, Chen Y J 2015 Opt. Express 23 18106
Google Scholar
[13] Zhou X, Lock R, Wagner N, Li W, Kapteyn H C, Murnane M M 2009 Phys. Rev. Lett. 102 073902
Google Scholar
[14] Levesque J, Mairesse Y, Dudovich N, epin H P, Kieffer J C, Corkum P B, Villeneuve D M 2007 Phys. Rev. Lett. 99 243001
Google Scholar
[15] Ramakrishna S, Sherratt P A J, Dutoi A D, Seideman T 2010 Phys. Rev. A 81 021802(R
Google Scholar
[16] Strelkov V V, Gonoskov A A, Gonoskov I A, Ryabikin M Yu 2011 Phys. Rev. Lett. 107 043902
Google Scholar
[17] Akagi H, Otobe T, Staudte A, Shiner A, Turner F, Dörner R, Villeneuve D M, Corkum P B 2009 Science 325 1364
Google Scholar
[18] Bian X B, Bandrauk A D 2010 Phys. Rev. Lett. 105 093903
Google Scholar
[19] Chen Y J, Zhang B 2011 Phys. Rev. A 84 053402
Google Scholar
[20] Qin M, Zhu X, Zhang Q, Hong W, Lu P 2011 Opt. Express 19 25084
Google Scholar
[21] Du H, Luo L, Wang X, Hu B 2012 Phys. Rev. A 86 013846
Google Scholar
[22] Yu S J, Zhang B, Li Y P, Yang S P, Chen Y J 2014 Phys. Rev. A 90 053844
Google Scholar
[23] Barreau L, Veyrinas K, Gruson V, Weber S J, Auguste T, Hergott J F, Lepetit F, Carré B, Houver J -C, Dowek D, Salières P 2018 Nat. Commun. 9 4727
Google Scholar
[24] Sun F J, Chen C, Li W Y, Liu X, Li W, Chen Y J 2021 Phys. Rev. A 103 053108
Google Scholar
[25] Habibović D, Milošević D B 2020 Photonics 7 110
Google Scholar
[26] Huo X X, Xing Y H, Qi T, Sun Y, Li Bo, Zhang J, Liu X S 2021 Phys. Rev. A 103 053116
Google Scholar
[27] Chen Y J 2011 Phys. Rev. A 84 043423
Google Scholar
[28] Chen Y J, Zhang B 2012 Phys. Rev. A 86 023415
Google Scholar
[29] Bian X B, Bandrauk A D 2012 Phys. Rev. A 86 053417
Google Scholar
[30] Miao X Y, Zhang C P 2014 Phys. Rev. A 89 033410
Google Scholar
[31] Han Y C 2013 Phys. Rev. A 87 043404
Google Scholar
[32] Feit M D, Jr Fleck J A, Steiger A 1982 J. Comput. Phys. 47 412
Google Scholar
[33] Shiner A D, Trallero-Herrero C, Kajumba N, Bandulet H C, Comtois D, Légaré F, Giguère M, Kieffffer J C, Corkum P B, Villeneuve D M 2009 Phys. Rev. Lett. 103 073902
Google Scholar
[34] Yu S J, Li W Y, Li Y P, Chen Y J 2017 Phys. Rev. A 96 013432
Google Scholar
[35] Chen Y J, Hu B 2009 J. Chem. Phys. 131 244109
Google Scholar
[36] Chen Y J, Chen J, Liu J 2006 Phys. Rev. A 74 063405
Google Scholar
下载:
计量
- 文章访问数: 2878
- PDF下载量: 80
- 被引次数: 0
