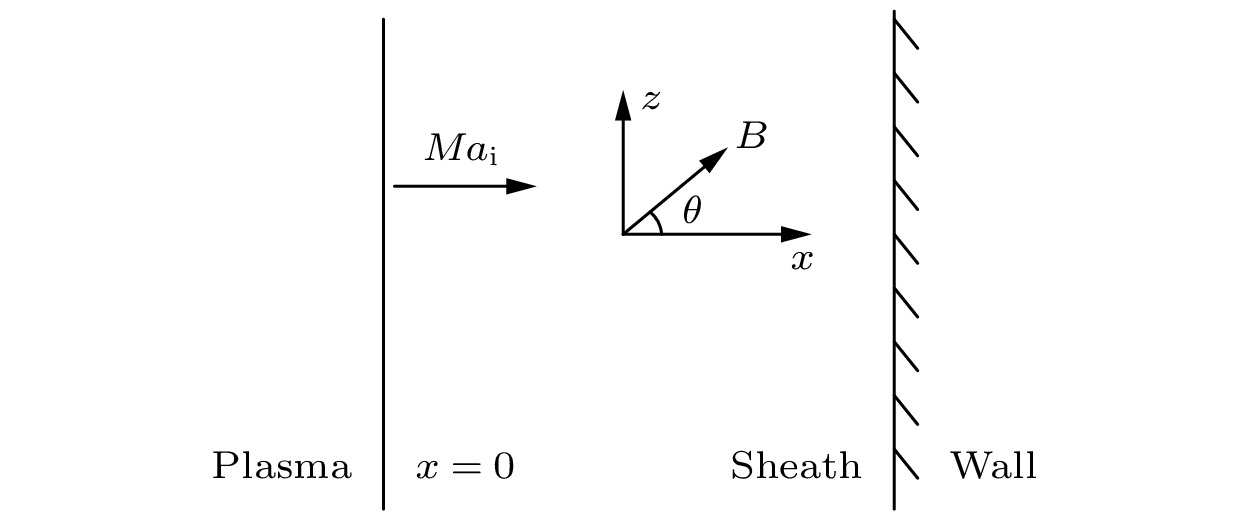
-
Many previous researches on the plasma sheath were based on the fact that the electrons satisfy the classical Maxwell velocity distribution function, while the particles in the plasma have long-range electromagnetic interactions. It is more appropriate to use the non-extensive distribution proposed by Tsallis to describe the electrons. In this paper, a collisional magnetized plasma sheath model with non-extensive distribution of electrons is established. Bohm criterion is derived theoretically. With the ion drift motion in the plasma pre-sheath region taken into consideration, the ion Mach number is only related to the angle of the magnetic field, the collision parameters, the electric field at the sheath edge, and non-extensive parameter
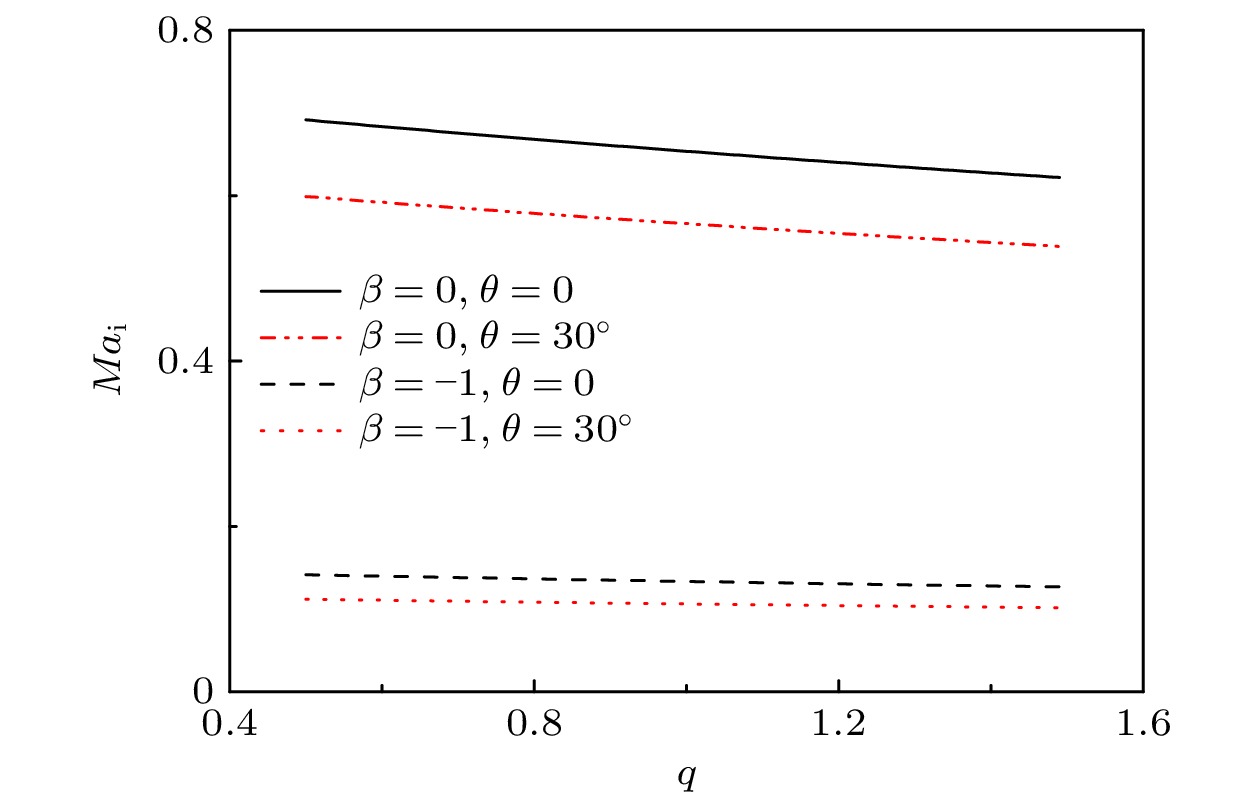
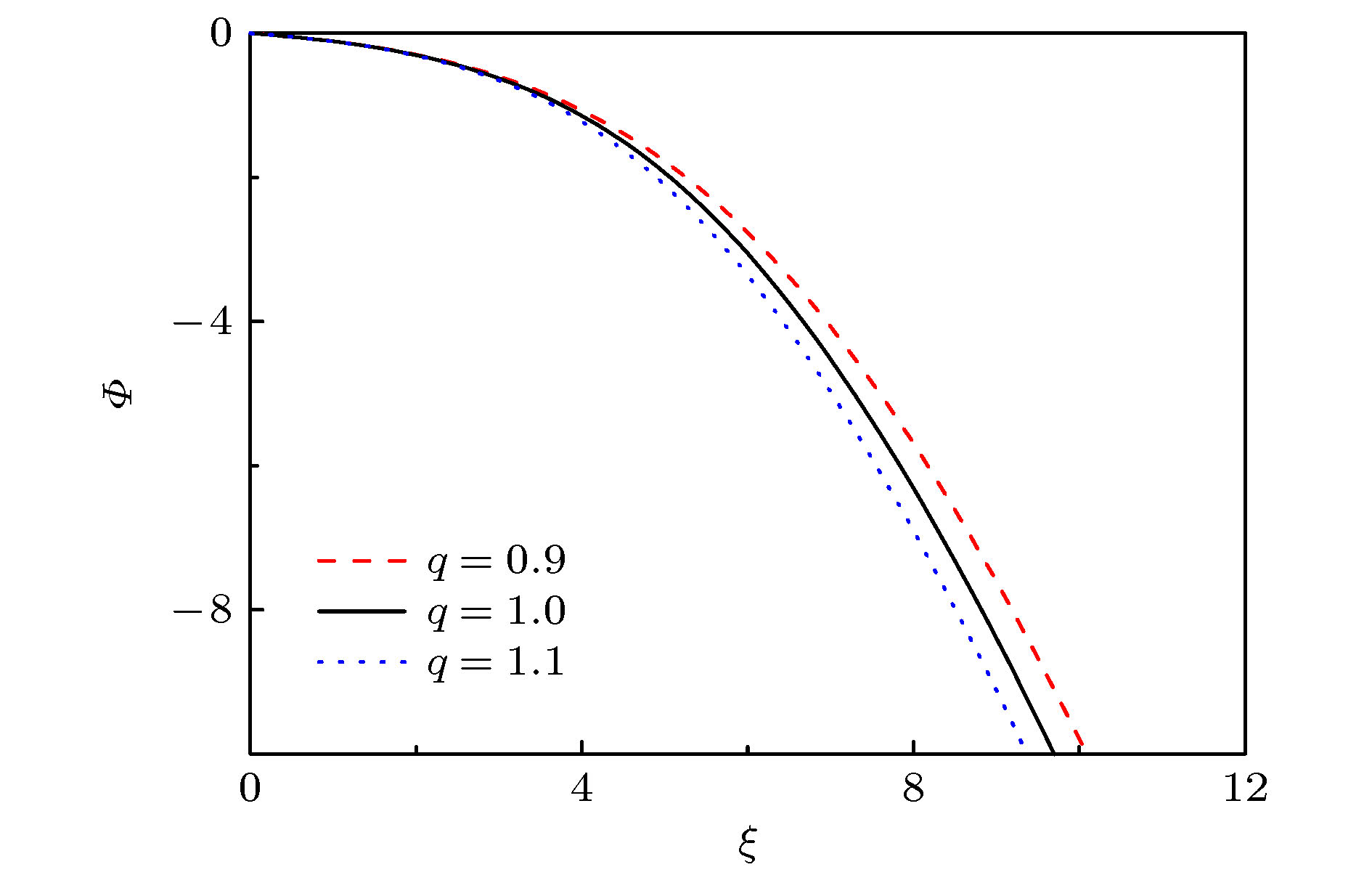
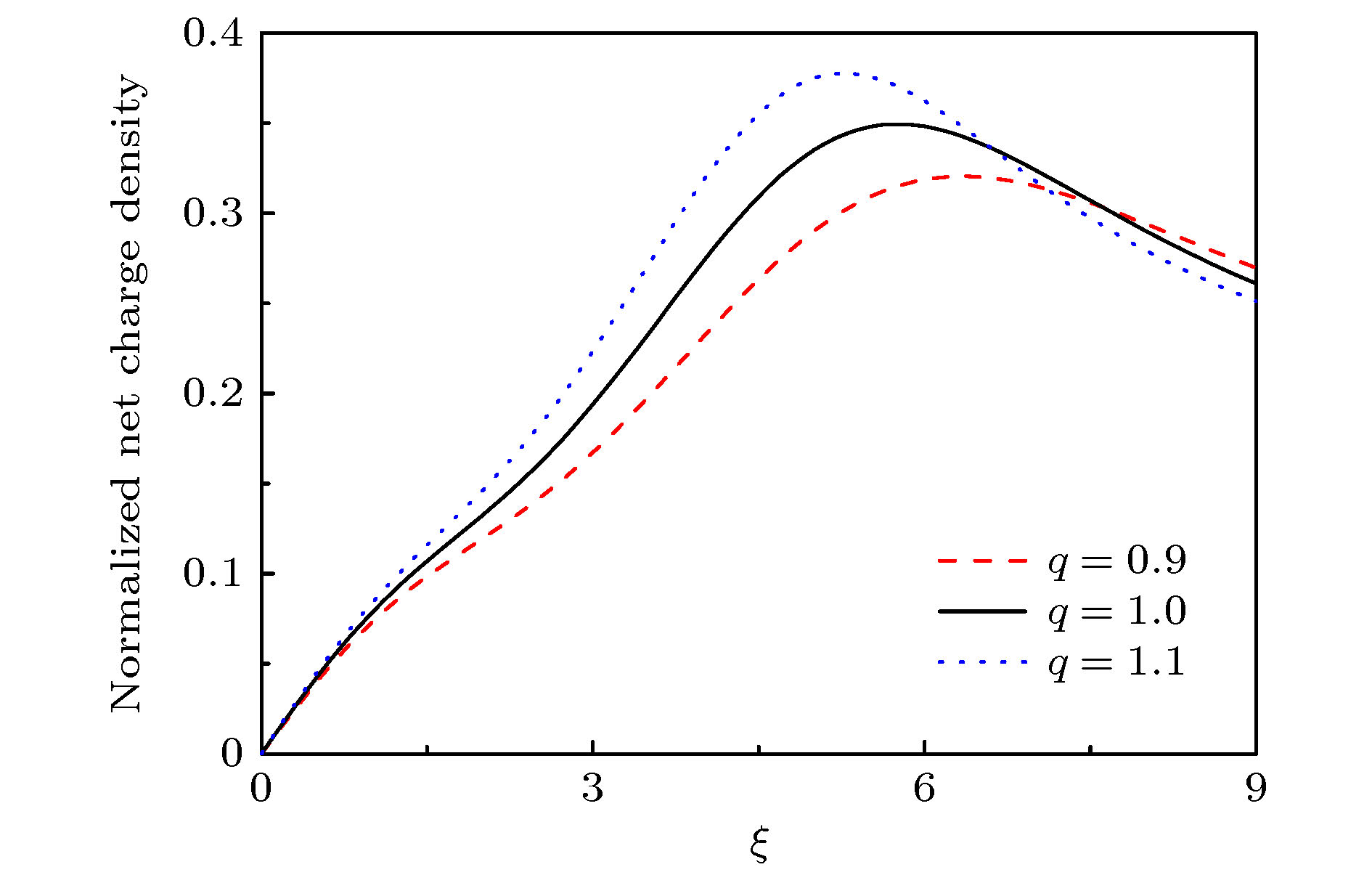
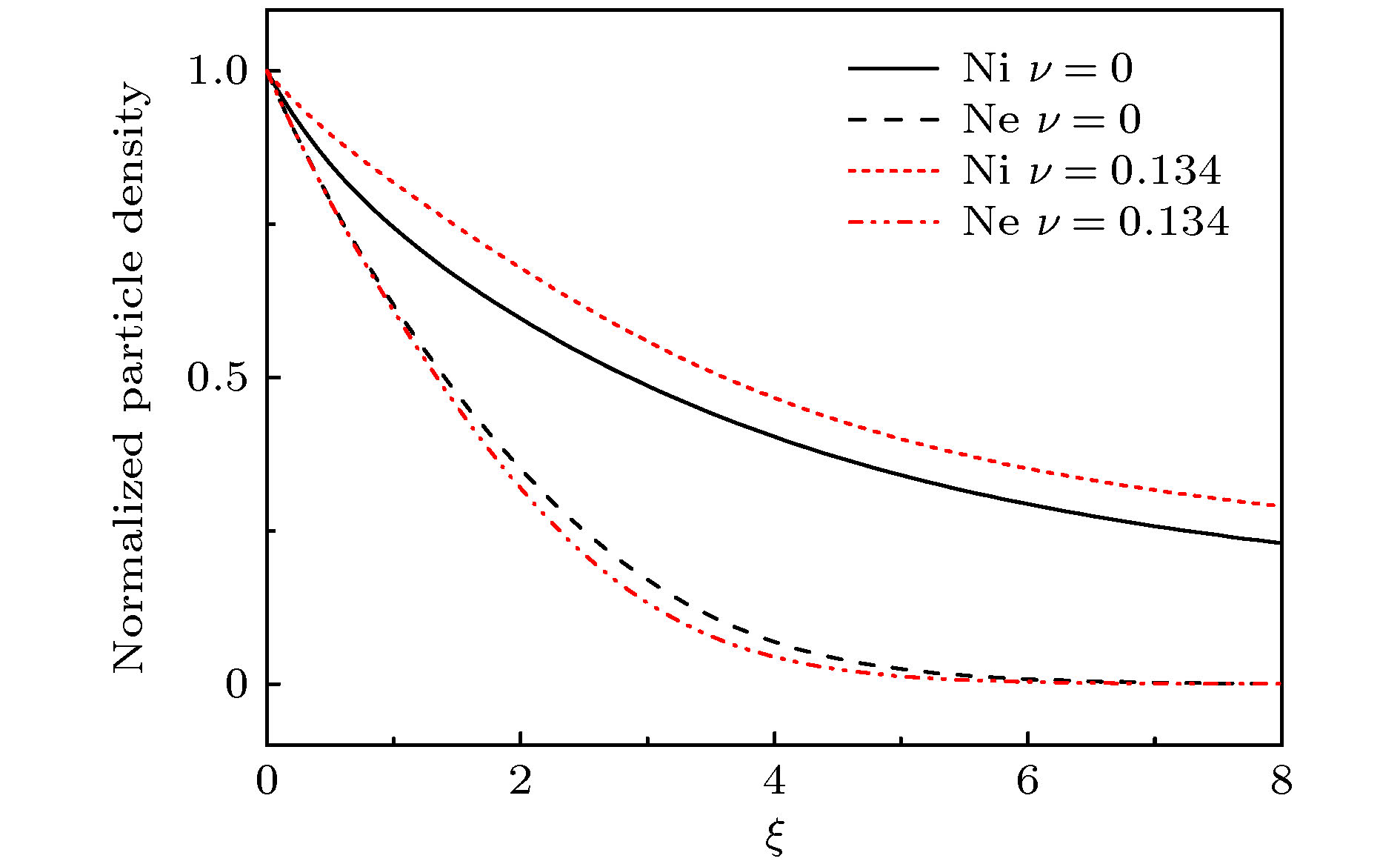
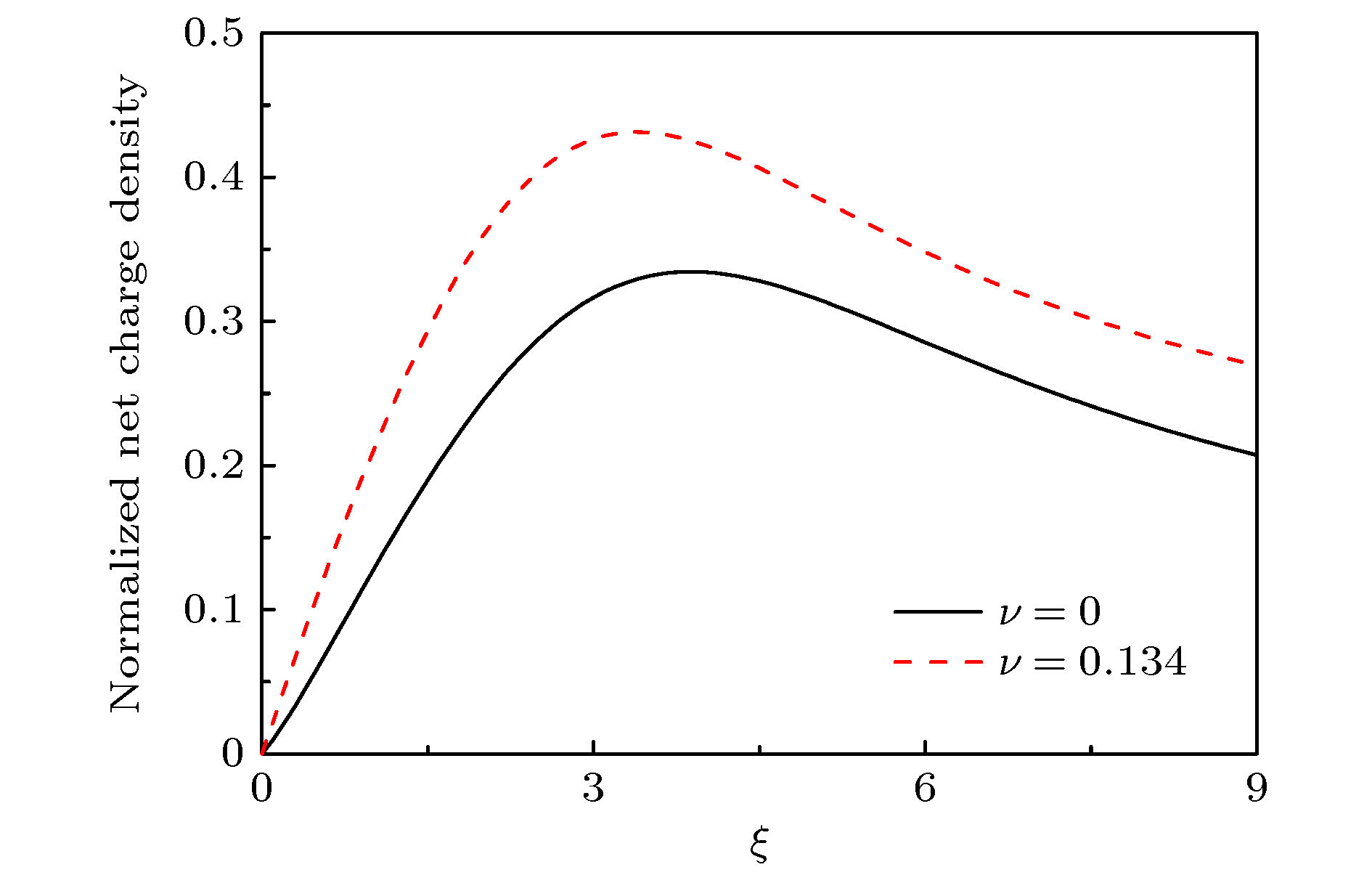
$ q $ . The influence of parameter$ q $ on the criterion is discussed in this paper. The lower limit of the ion Mach number changes with the value of parameter$ q $ . The lower limit of the ion Mach number increases for$ q < 1 $ . And the lower limit of the ion Mach number decreases for$ q>1 $ . With the increase of$ q $ , the number of electrons with lower speed increases, ions need less kinetic energy to enter into the sheath and thus enter into the sheath more easily. Through numerical simulation, it is found that compared with the structure of the plasma magnetized sheath with Maxwell distribution ($ q=1 $ ), the structure of the plasma magnetized sheath with super-extensive distribution ($ q < 1 $ ) and that with sub-extensive ($ q>1 $ ) are different, including the distribution of the space potential, the ion density, the electron density, and the space charge density. When$ q < 1 $ , the space potential, the electron density and the ion density fall more slowly, and the peak of the space charge density curve is closer to the wall. When$ q>1 $ , the space potential and the ion electron density fall faster, especially the electron density drops to zero faster, and the peak of the space charge density curve is far away from the wall. The simulation results show that the non-extensive parameter$ q $ has a significant influence on the structure of collisional plasma magnetized sheath. The influence of the collision on the magnetized plasma sheath with non-extensive distribution is similar to that with the Maxwell distribution. These conclusions may be useful in solving the problems of plasma boundary.-
Keywords:
- non-extensive distribution /
- plasma /
- sheath
[1] Chodura R 1982 Phys. Fluid 25 1628
Google Scholar
[2] Riemann K U 1994 Phys. Plasmas 1 552
Google Scholar
[3] Stangeby P C 1995 Phys. Plasmas 2 702
Google Scholar
[4] Ahedo E 1997 Phys. Plasmas 4 4419
Google Scholar
[5] Liu J Y, Wang Z X, Wang X G 2003 Phys. Plasmas 10 3032
Google Scholar
[6] Liu J Y, Wang Z X, Wang X G, Zhang Q, Zou X 2003 Phys. Plasmas 10 3507
Google Scholar
[7] 王正汹, 刘金远, 邹秀, 刘悦, 王晓刚 2004 53 0793
Google Scholar
Wang Z X, Liu J Y, Zou X, Liu Y, Wang X G 2004 Acta Phys. Sin. 53 0793
Google Scholar
[8] 邹秀, 刘金远, 王正汹 2004 53 3409
Google Scholar
Zou X, Liu J Y, Wang Z X 2004 Acta Phys. Sin. 53 3409
Google Scholar
[9] Masoudi S F 2007 Vacuum 81 871
Google Scholar
[10] 邹秀, 刘惠平, 谷秀娥 2008 57 5111
Google Scholar
Zou X, Liu H P, Gu X E 2008 Acta Phys. Sin. 57 5111
Google Scholar
[11] 刘惠平, 邹秀, 邹滨雁, 邱明辉 2016 65 245201
Google Scholar
Liu H P, Zou X, Zou B Y, Qiu M H 2016 Acta Phys. Sin. 65 245201
Google Scholar
[12] 邹秀, 籍延坤, 邹滨雁 2010 59 1902
Google Scholar
Zou X, Ji Y K, Zou B Y 2010 Acta Phys. Sin. 59 1902
Google Scholar
[13] 刘惠平, 邹秀 2020 69 025201
Google Scholar
Liu H P, Zou X 2020 Acta Phys. Sin. 69 025201
Google Scholar
[14] Hatami M M 2015 Phys. Plasmas 22 013508
Google Scholar
[15] Hatami M M 2015 Phys. Plasmas 22 023506
Google Scholar
[16] Hatami M M, Tribeche M, Mamun A A 2018 Phys. Plasmas 25 094502
Google Scholar
[17] Borgohain D R, Saharia K, Goswami K S 2016 Phys. Plasmas 23 122113
Google Scholar
[18] Borgohain D R, Saharia K 2018 Phys. Plasmas 25 032122
Google Scholar
[19] 赵晓云, 张丙开, 王春晓, 唐义甲 2019 68 185204
Google Scholar
Zhao X Y, Zhang B K, Wang C X, Tang Y J 2019 Acta Phys. Sin. 68 185204
Google Scholar
[20] Liu Y, Liu S Q, Xu K 2012 Phys. Plasmas 19 073702
Google Scholar
[21] Liu Y, Liu S Q, Zhou L 2013 Phys. Plasmas 20 043702
Google Scholar
[22] Tantawy S A E, Tribeche M, Moslem W M 2012 Phys. Plasmas 19 032104
Google Scholar
[23] Emamuddin M, Yasmin S, Asaduzzaman M, Mamun A A 2013 Phys. Plasmas 20 083708
Google Scholar
[24] Safa N N, Ghomi H, Niknam A R 2014 Phys. Plasmas 21 082111
Google Scholar
[25] Mehdipoor M, Mohsenpour T 2015 Phys. Plasmas 22 112110
Google Scholar
[26] Gougam L A, Triceche M 2011 Phys. Plasmas 18 062102
Google Scholar
[27] Liu J Y, Wang F, Sun J Z 2011 Phys. Plasmas 18 013506
Google Scholar
[28] Ou J, Yang J H 2012 Phys. Plasmas 19 113504
Google Scholar
[29] Li J J, Ma J X, Wei Z A 2013 Phys. Plasmas 20 063503
Google Scholar
[30] Wang T T, Ma J X, Wei Z A 2015 Phys. Plasmas 22 093505
Google Scholar
[31] Tsallis C 1988 J. Stat. Phys. 52 479
Google Scholar
-
图 1 等离子体磁鞘模型示意图
Figure 1. Schematic diagram of plasma magnetic sheath model.
图 2 离子马赫数的下限随参数
$ q $ 的变化 ($B=0.3~\mathrm{T}$ ,$ {E}_{0}=0.1 $ )Figure 2. Ion Mach number versus non-extensive parameter
$ q $ ($B=0.3~\mathrm{T}$ ,$ {E}_{0}=0.1 $ ).
图 3 具有不同参数
$ q $ 值的鞘层空间电势($B=0.3~\mathrm{T}$ ,$ \theta =15° $ ,$ {E}_{0}=0.1 $ ,$ \beta =0 $ )Figure 3. Sheath potential for different values of non-extensive parameter
$ q $ ($B=0.3~\mathrm{T}$ ,$ \theta =15° $ ,$ {E}_{0}=0.1 $ ,$ \beta =0 $ ).
图 5 具有不同参数
$ q $ 值的鞘层空间电荷密度分布 ($B= 0.3~\mathrm{T}$ ,$ \theta =15° $ ,$ {E}_{0}=0.1 $ ,$ \beta =0 $ )Figure 5. Normalized space charge density for different values of non-extensive parameter
$ q $ ($B=0.3~\mathrm{T}$ ,$ \theta =15° $ ,${E}_{0}= 0.1$ ,$ \beta =0 $ ).
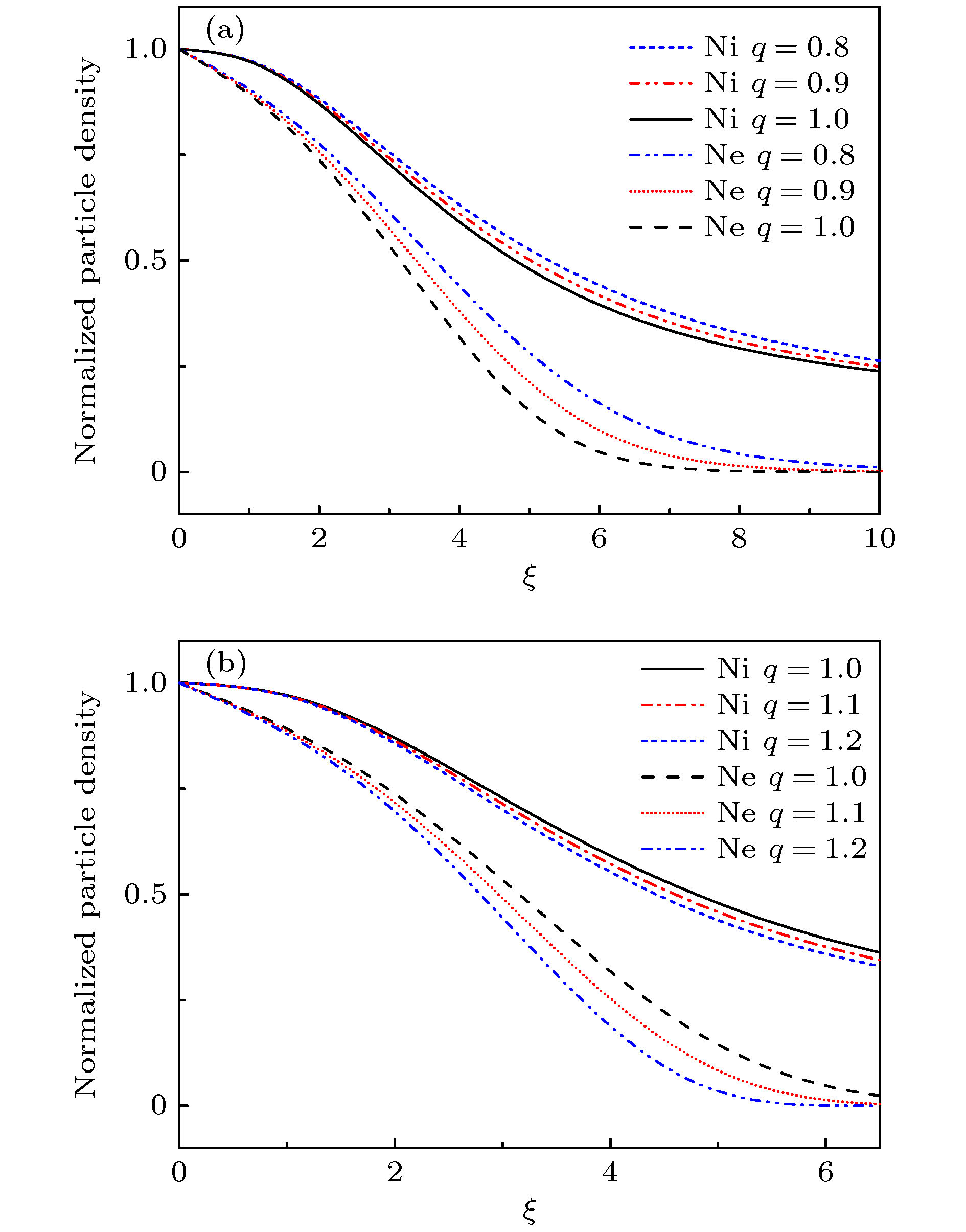
图 4 具有不同参数
$ q $ 值的离子电子密度分布($B=0.3~\mathrm{T}$ ,$ \theta =15° $ ,$ {E}_{0}=0.1 $ ,$ \beta =0 $ ) (a)$ q < 1 $ ; (b$ )q>1 $ Figure 4. Normalized density of ions and electrons for different values of non-extensive parameter
$ q $ ($B=0.3~\mathrm{T}$ ,$ \theta =15° $ ,$ {E}_{0}=0.1 $ ,$ \beta =0 $ ): (a)$ q < 1 $ ; (b)$ q>1 $ 
图 6 具有不同碰撞参数
$ \nu $ 值的离子电子密度分布($B= 0.3~\mathrm{T}$ ,$ \theta =15° $ ,$ {E}_{0}=0.5 $ ,$ \beta =0 $ ,$ q=0.9 $ )Figure 6. Normalized density of ions and electrons for different values of collision parameter
$ \nu $ ($B=0.3~\mathrm{T}$ ,$ \theta =15° $ ,$ {E}_{0}=0.5, \beta =0 $ ,$ q=0.9 $ ).
图 7 具有不同碰撞参数
$ \nu $ 值的鞘层空间电荷密度分布 ($B= 0.3~\mathrm{T}$ ,$ \theta =15° $ ,$ {E}_{0}=0.5 $ ,$ \beta =0 $ ,$ q=0.9 $ )Figure 7. Normalized space charge density for different values of collision parameter
$ \nu $ ($B=0.3~\mathrm{T}$ ,$ \theta =15° $ ,$ {E}_{0}=0.5 $ ,$ \beta =0 $ ,$ q=0.9 $ ) -
[1] Chodura R 1982 Phys. Fluid 25 1628
Google Scholar
[2] Riemann K U 1994 Phys. Plasmas 1 552
Google Scholar
[3] Stangeby P C 1995 Phys. Plasmas 2 702
Google Scholar
[4] Ahedo E 1997 Phys. Plasmas 4 4419
Google Scholar
[5] Liu J Y, Wang Z X, Wang X G 2003 Phys. Plasmas 10 3032
Google Scholar
[6] Liu J Y, Wang Z X, Wang X G, Zhang Q, Zou X 2003 Phys. Plasmas 10 3507
Google Scholar
[7] 王正汹, 刘金远, 邹秀, 刘悦, 王晓刚 2004 53 0793
Google Scholar
Wang Z X, Liu J Y, Zou X, Liu Y, Wang X G 2004 Acta Phys. Sin. 53 0793
Google Scholar
[8] 邹秀, 刘金远, 王正汹 2004 53 3409
Google Scholar
Zou X, Liu J Y, Wang Z X 2004 Acta Phys. Sin. 53 3409
Google Scholar
[9] Masoudi S F 2007 Vacuum 81 871
Google Scholar
[10] 邹秀, 刘惠平, 谷秀娥 2008 57 5111
Google Scholar
Zou X, Liu H P, Gu X E 2008 Acta Phys. Sin. 57 5111
Google Scholar
[11] 刘惠平, 邹秀, 邹滨雁, 邱明辉 2016 65 245201
Google Scholar
Liu H P, Zou X, Zou B Y, Qiu M H 2016 Acta Phys. Sin. 65 245201
Google Scholar
[12] 邹秀, 籍延坤, 邹滨雁 2010 59 1902
Google Scholar
Zou X, Ji Y K, Zou B Y 2010 Acta Phys. Sin. 59 1902
Google Scholar
[13] 刘惠平, 邹秀 2020 69 025201
Google Scholar
Liu H P, Zou X 2020 Acta Phys. Sin. 69 025201
Google Scholar
[14] Hatami M M 2015 Phys. Plasmas 22 013508
Google Scholar
[15] Hatami M M 2015 Phys. Plasmas 22 023506
Google Scholar
[16] Hatami M M, Tribeche M, Mamun A A 2018 Phys. Plasmas 25 094502
Google Scholar
[17] Borgohain D R, Saharia K, Goswami K S 2016 Phys. Plasmas 23 122113
Google Scholar
[18] Borgohain D R, Saharia K 2018 Phys. Plasmas 25 032122
Google Scholar
[19] 赵晓云, 张丙开, 王春晓, 唐义甲 2019 68 185204
Google Scholar
Zhao X Y, Zhang B K, Wang C X, Tang Y J 2019 Acta Phys. Sin. 68 185204
Google Scholar
[20] Liu Y, Liu S Q, Xu K 2012 Phys. Plasmas 19 073702
Google Scholar
[21] Liu Y, Liu S Q, Zhou L 2013 Phys. Plasmas 20 043702
Google Scholar
[22] Tantawy S A E, Tribeche M, Moslem W M 2012 Phys. Plasmas 19 032104
Google Scholar
[23] Emamuddin M, Yasmin S, Asaduzzaman M, Mamun A A 2013 Phys. Plasmas 20 083708
Google Scholar
[24] Safa N N, Ghomi H, Niknam A R 2014 Phys. Plasmas 21 082111
Google Scholar
[25] Mehdipoor M, Mohsenpour T 2015 Phys. Plasmas 22 112110
Google Scholar
[26] Gougam L A, Triceche M 2011 Phys. Plasmas 18 062102
Google Scholar
[27] Liu J Y, Wang F, Sun J Z 2011 Phys. Plasmas 18 013506
Google Scholar
[28] Ou J, Yang J H 2012 Phys. Plasmas 19 113504
Google Scholar
[29] Li J J, Ma J X, Wei Z A 2013 Phys. Plasmas 20 063503
Google Scholar
[30] Wang T T, Ma J X, Wei Z A 2015 Phys. Plasmas 22 093505
Google Scholar
[31] Tsallis C 1988 J. Stat. Phys. 52 479
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 5239
- PDF Downloads: 66
- Cited By: 0
