-
The blackout problem suffered by hypersonic vehicles as they re-enter the atmosphere is essential for effective communication of hypersonic vehicles. Aiming to solve this problem, in this paper, we proposed an antenna–sheath–plasma layer configuration, in which a thin plasma layer covered cylindrical metal antenna model is employed to investigate the radiation enhancement phenomenon by solving the dispersion equation of electromagnetic mode under optimized parameter conditions. Analytical results show that when the neutral gas pressure is low (p = 0.5 mTorr) and the antenna radius is triple the plasma skin depth, the thickness of the sheath between the surface of metal cylindrical antenna and plasma layer is about several Debye lengths, the azimuthally symmetric wave (m = 0 mode) that propagates along the antenna surface belongs to the fast wave (the phase velocity is greater than the light speed), there exists a critical plasma frequency ωpe (or plasma density n0), above which the propagating mode becomes evanescent wave; for the propagation characteristic, there exists a critical normalized sheath thickness (ι/λDe)pha (or (ι/λDe)att), above which the phase constant (or the attenuation constant) begins to increase (or decrease) sharply, which indicates a significant change in the propagation property of the propagating mode; most importantly, when the wave frequency ω/2π = 1 GHz, sheath thickness is one tenth of the whole plasma layer thickness, owing to the electron plasma frequency resonance and antenna-sheath-plasma resonance effect, the maximum radiation intensity of the symmetric wave exhibits an elliptical-like profile near ωpe/ω = 1 and ωpe/ω ≈ 1.33, respectively, while only a single-point radiation enhancement occurs at frequencies far from GHz range. These conclusions not only provide a method to solve or alleviate the blackout problem of GHz frequency communication faced by the hypersonic vehicles when they re-enter the atmosphere, but also have potential applications in high-resolution imaging induced by plasmonic micro-nano sized enhanced radiation and high-resolution phased array antennas.
-
Keywords:
- plasma /
- sheath /
- electromagnetic wave radiation /
- dispersion relation
[1] Kumar N, Vadera S R 2017 Aerospace Materials and Material Technologies (Singapore: Springer) p519
[2] Ananth P B, Abhiram N, Krishna K H, et al. 2021 Mater. Today Proc. 47 4872
Google Scholar
[3] Ghayekhloo A, Abdolali A, Armaki S H M 2017 IEEE Trans. Antennas Propag. 65 3058
Google Scholar
[4] Dong B, Ma Y, Ren Z, et al. 2020 J. Phys. D: Appl. Phys. 53 213001
Google Scholar
[5] Koya A N, Cunha J, Guerrero-Becerra K A, Garoli D, Wang T, Juodkazis S, Zaccaria R P 2021 Adv. Funct. Mater. 31 2103706
Google Scholar
[6] 李盼 2019 68 146201
Google Scholar
Li P 2019 Acta Phys. Sin. 68 146201
Google Scholar
[7] 陆云清, 呼斯楞, 陆懿, 许吉, 王瑾 2015 64 077303
Google Scholar
Lu Y Q, Hu S L, Lu Y, Xu J, Wang J 2015 Acta Phys. Sin. 64 077303
Google Scholar
[8] Webb B A, Ziolkowski R W 2020 Photonics 7 88
Google Scholar
[9] Kim M, Boyd I D, Keidar M 2010 J. Spacecr. Rockets 47 29
Google Scholar
[10] Pinder D N 1965 Electron. Lett. 10 291
Google Scholar
[11] Messiaen A M, Vandenplas P E 1967 Electron. Lett. 1 26
Google Scholar
[12] Lin C C, Chen K M 1970 IEEE Trans. Antennas Propag. 18 831
Google Scholar
[13] Freeman E M, Lin C C, Chen K M 1971 Proc. Inst. Electr. Eng. 118 1748
Google Scholar
[14] Gao X T, Wang C S, Jiang B, Zhang Z L 2014 Phys. Plasmas 21 093301
Google Scholar
[15] Wang C S, Li X, Jiang B 2015 Appl. Phys. Lett. 106 102901
Google Scholar
[16] Mouzouris Y, Scharer J E 1998 Phys. Plasmas 5 4253
Google Scholar
[17] Virko V F, Kirichenko G S, Shamrai K P 2002 Plasma Sources Sci. Technol. 11 10
Google Scholar
[18] Niemi K, Krämer M 2008 Phys. Plasmas 15 073503
Google Scholar
[19] Shamrai K P, Shinohara S 2001 Phys. Plasmas 8 4659
Google Scholar
[20] Huba J D 2016 NRL Plasma Formulary (Washington: Naval Research Laboratory) p34
[21] Fried B D, Conte S D 2015 The Plasma Dispersion Function: The Hilbert Transform of the Gaussian (New York: Academic Press) p1
[22] Glaude V M M, Moisan M, Pantel R, Leprince P, Marec J 1980 J. Appl. Phys. 51 5693
Google Scholar
[23] Jackson J D 1999 Classical Electrodynamics (New York: John Wiley & Sons) p176
[24] Swanson D G 1989 Plasma Waves (New York: Academic Press) p155
[25] Stix T H 1992 Waves in Plasmas (New York: Springer Verlag) p72
[26] Chen F F, Arnush D 2001 Phys. Plasmas 8 5051
Google Scholar
-
图 1 等离子体覆盖金属天线系统示意图
Figure 1. A sketch of the plasma layer coated metal antenna system.
图 2 等离子体频率为ωpe/(2π) = 10 GHz时, 天线半径对鞘层厚度与电子温度依赖关系的影响
Figure 2. Impact of antenna radius on sheath thickness versus electron temperature relation for plasma frequency ωpe/(2π) = 10 GHz.
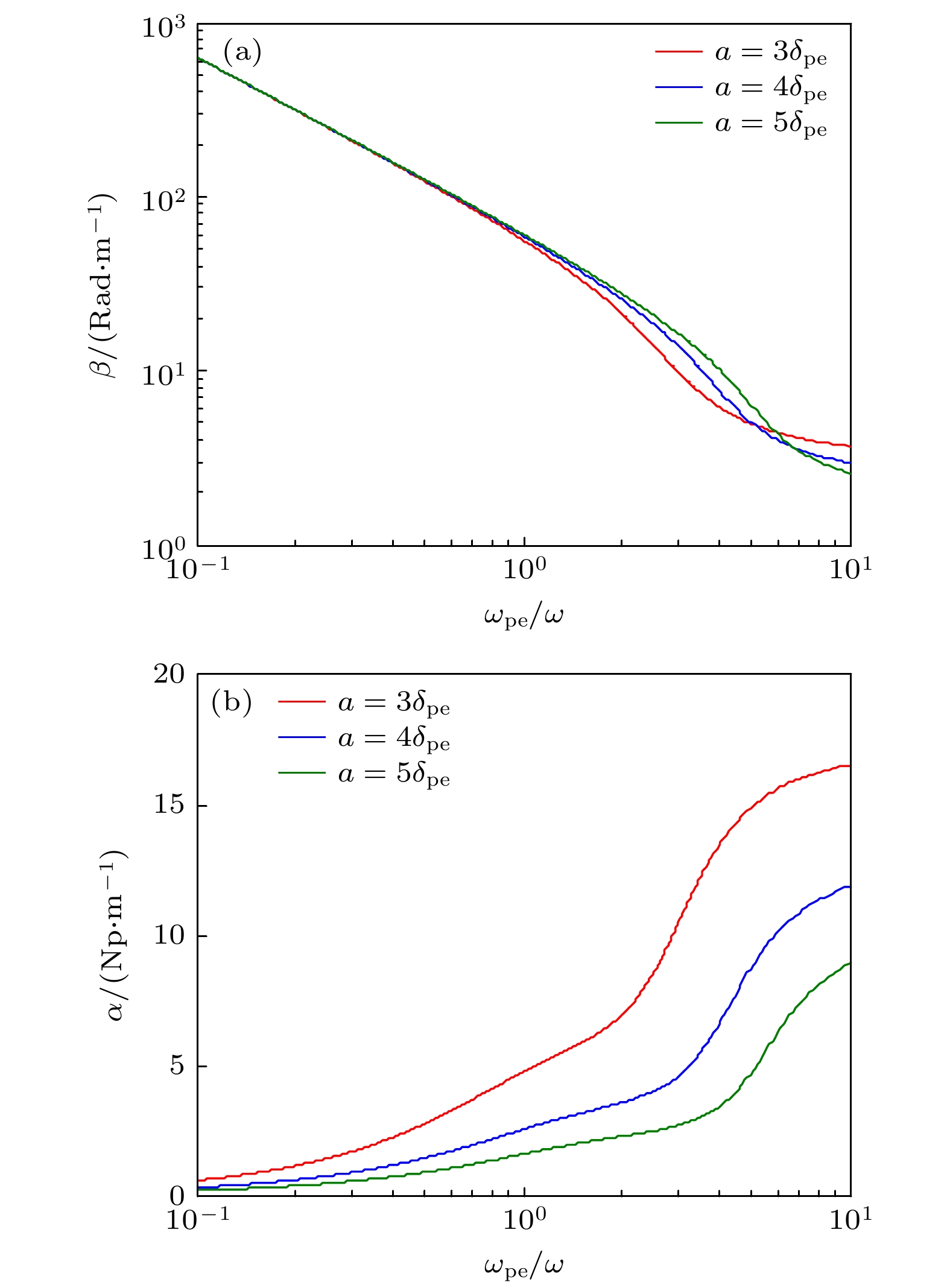
图 3 ω/(2π) = 1 GHz,
${T_{\text{e}}} = 3{\text{ eV}}$ ,$p = 0.5{\text{ mTorr}}$ ,$a = $ $ 3\max \{ {\delta _{{\text{pe}}}}\}$ 时, 相位常数和衰减常数与归一化等离子体频率的依赖关系Figure 3. Phase and attenuation constant versus electron temperature for wave frequency ω/(2π) = 1 GHz,
${T_{\text{e}}} = 3{\text{ eV}}$ ,$p = 0.5{\text{ mTorr}}$ ,$a = 3\max \{ {\delta _{{\text{pe}}}}\} $ .
图 4 等离子体频率为ωpe/(2π) = 3 GHz时, 天线半径对色散关系的影响
Figure 4. Impact of antenna radius on dispersion relation for plasma frequency ωpe/(2π) = 3 GHz.
图 5
$\omega /(2{\text{π }}) = 3{\text{ GHz}}$ ,${\omega _{{\text{pe}}}} = 3\omega $ ,$p = 0.5{\text{ mTorr}}$ ,$a = 3{\delta _{{\text{pe}}}}$ 时, 电磁波在主等离子体区域的功率损耗随归一化相速的变化关系Figure 5. Power loss of electromagnetic waves in the main plasma region vs. the normalized phase velocity at
$\omega /(2{\text{π }}) = $ $ 3{\text{ GHz}}$ ,${\omega _{{\text{pe}}}} = 3\omega $ ,$p = 0.5{\text{ mTorr}}$ ,$a = 3{\delta _{{\text{pe}}}}$ .
图 6 ωpe/(2π) = 3 GHz时, 天线半径对色散关系的影响 (a)相位常数; (b)衰减常数
Figure 6. Impact of antenna radius on dispersion relation at ωpe/(2π) = 3 GHz: (a) Phase constant; (b) attenuation constant.
图 7 ω/(2π) = 1 GHz时, 不同常数与归一化鞘层厚度的依赖关系 (a)相位常数; (b)衰减常数
Figure 7. Dependence of different constant on normalized sheath thickness at ω/(2π) = 1 GHz: (a) Phase constant; (b) attenuation constant.
图 8 总电场|E|在(
${\omega _{\rm pe}}/\omega , {\text{ }}{T_{\text{e}}}$ )参量空间的三维分布Figure 8. Three-dimensional electric field distribution in the parameter space of (
${\omega _{\rm pe}}/\omega , ~{T_{\text{e}}}$ ).
图 9 辐射功率Prad在(
${\omega _{{\text{pe}}}}/\omega , {\text{ }}{T_{\text{e}}}$ )参量空间的分布Figure 9. Radiation power of electromagnetic waves in the parameter space of (
${\omega _{{\text{pe}}}}/\omega , ~{T_{\text{e}}}$ ). -
[1] Kumar N, Vadera S R 2017 Aerospace Materials and Material Technologies (Singapore: Springer) p519
[2] Ananth P B, Abhiram N, Krishna K H, et al. 2021 Mater. Today Proc. 47 4872
Google Scholar
[3] Ghayekhloo A, Abdolali A, Armaki S H M 2017 IEEE Trans. Antennas Propag. 65 3058
Google Scholar
[4] Dong B, Ma Y, Ren Z, et al. 2020 J. Phys. D: Appl. Phys. 53 213001
Google Scholar
[5] Koya A N, Cunha J, Guerrero-Becerra K A, Garoli D, Wang T, Juodkazis S, Zaccaria R P 2021 Adv. Funct. Mater. 31 2103706
Google Scholar
[6] 李盼 2019 68 146201
Google Scholar
Li P 2019 Acta Phys. Sin. 68 146201
Google Scholar
[7] 陆云清, 呼斯楞, 陆懿, 许吉, 王瑾 2015 64 077303
Google Scholar
Lu Y Q, Hu S L, Lu Y, Xu J, Wang J 2015 Acta Phys. Sin. 64 077303
Google Scholar
[8] Webb B A, Ziolkowski R W 2020 Photonics 7 88
Google Scholar
[9] Kim M, Boyd I D, Keidar M 2010 J. Spacecr. Rockets 47 29
Google Scholar
[10] Pinder D N 1965 Electron. Lett. 10 291
Google Scholar
[11] Messiaen A M, Vandenplas P E 1967 Electron. Lett. 1 26
Google Scholar
[12] Lin C C, Chen K M 1970 IEEE Trans. Antennas Propag. 18 831
Google Scholar
[13] Freeman E M, Lin C C, Chen K M 1971 Proc. Inst. Electr. Eng. 118 1748
Google Scholar
[14] Gao X T, Wang C S, Jiang B, Zhang Z L 2014 Phys. Plasmas 21 093301
Google Scholar
[15] Wang C S, Li X, Jiang B 2015 Appl. Phys. Lett. 106 102901
Google Scholar
[16] Mouzouris Y, Scharer J E 1998 Phys. Plasmas 5 4253
Google Scholar
[17] Virko V F, Kirichenko G S, Shamrai K P 2002 Plasma Sources Sci. Technol. 11 10
Google Scholar
[18] Niemi K, Krämer M 2008 Phys. Plasmas 15 073503
Google Scholar
[19] Shamrai K P, Shinohara S 2001 Phys. Plasmas 8 4659
Google Scholar
[20] Huba J D 2016 NRL Plasma Formulary (Washington: Naval Research Laboratory) p34
[21] Fried B D, Conte S D 2015 The Plasma Dispersion Function: The Hilbert Transform of the Gaussian (New York: Academic Press) p1
[22] Glaude V M M, Moisan M, Pantel R, Leprince P, Marec J 1980 J. Appl. Phys. 51 5693
Google Scholar
[23] Jackson J D 1999 Classical Electrodynamics (New York: John Wiley & Sons) p176
[24] Swanson D G 1989 Plasma Waves (New York: Academic Press) p155
[25] Stix T H 1992 Waves in Plasmas (New York: Springer Verlag) p72
[26] Chen F F, Arnush D 2001 Phys. Plasmas 8 5051
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 2767
- PDF Downloads: 79
- Cited By: 0
