-
Optical Schrödinger cat state is not only one of the basic elements of quantum mechanics, but also a pivotal resource of continuous-variable quantum information. The non-Gaussian operation in its preparation can also be a key technology in distilling continuous-variable squeezing and entanglement. In the experimental preparation, a small part of a beam of vacuum squeezing is separated and detected as the trigger of appearance of Schrödinger cat state. Filter operation in the trigger optical path is important since it affects dark counts of single photon detector, frequency mode matching of trigger mode and signal mode, and preparing rate of the Schrödinger cat state, etc. In this paper, we describe the design of optical filter in the trigger path and the measurement of the filter cavity length. According to the design, filter cavity length
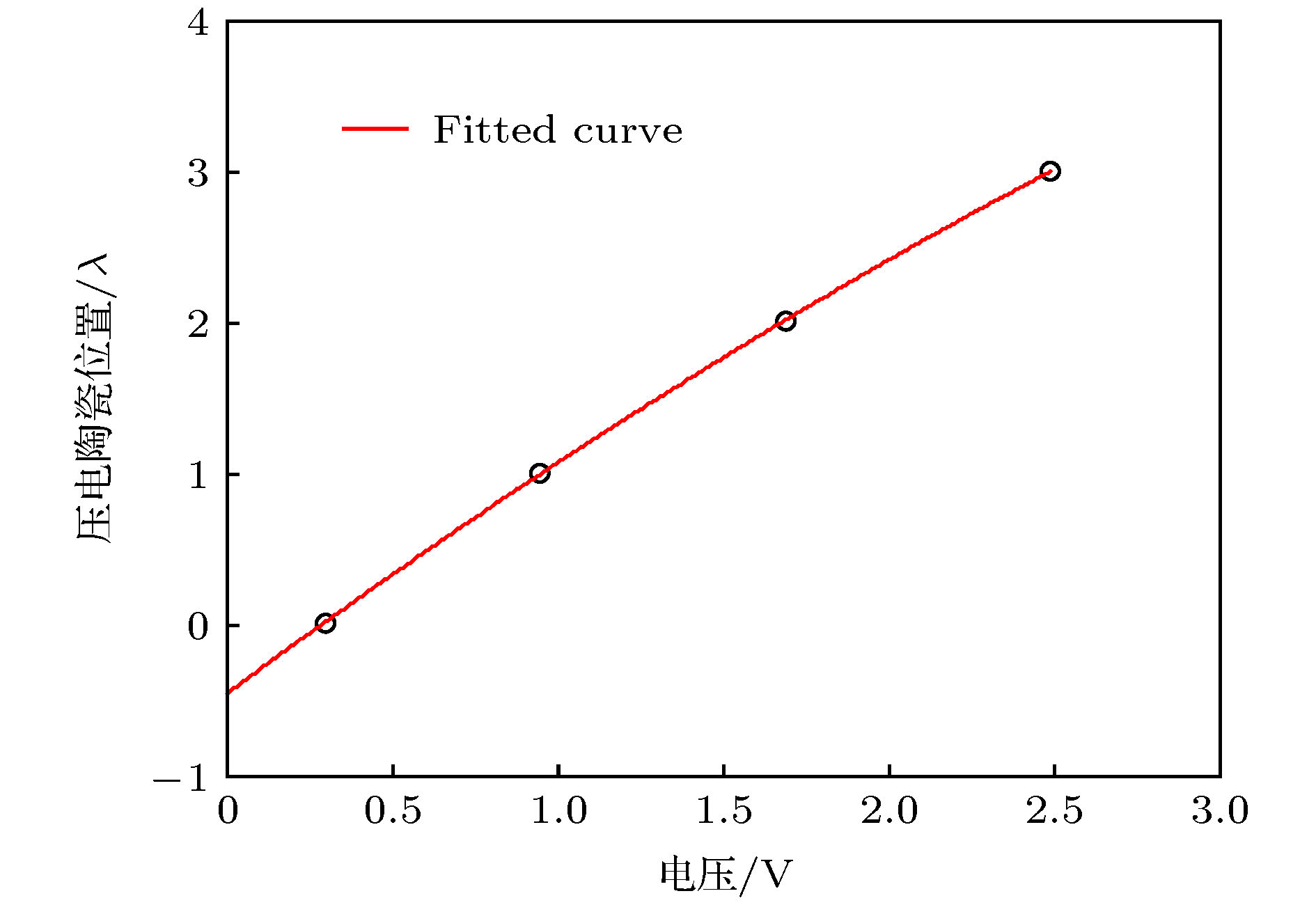
$ {l_{{\rm{FC}}}}$ should satisfy$ {\rm{189}}\;{\text{μm}} > {l_{{\rm{FC}}}} > {\rm{119}}\;{\text{μm}}$ . This cavity length is too small to be measured with a ruler. To measure the cavity length, we introduce an optical method, in which Gouy phases of Hermite Gaussian transverse modes TEM00 and TEM10 are used. When the cavity length is scanned, resonant peaks and the corresponding scanning voltages are recorded. From theoretical derivation, the cavity length is related to the filter cavity piezo response to the scanning voltage$ {\varPsi '_{\rm{G}}}$ , the slope rate of piezo scanning voltage$ U'$ , and the time distance between TEM00 and TEM10 resonant peaks$ \Delta t$ . The finally measured cavity length is${l_{{\rm{FC}}}} = ({\rm{141}} \pm 28)~{\text{μm}}$ , which satisfies the design requirement. The measurement error mainly originates from inaccurate fitting of$ {\varPsi '_{\rm{G}}}$ and$ U'$ , and readout error of$ \Delta t$ . It is shown that the error of$ {\varPsi '_{\rm{G}}}$ is dominant since less data are used in the curve fitting. The measurement error is expected to be reduced if much more data of piezo response to scanning voltage are collected and used to fit$ {\varPsi '_{\rm{G}}}$ with higher order polynomials. The proposed measurement method of short cavity length needs neither wide tuning laser nor any peculiar instrument, and does not depend on any dispersion property of the cavity, and hence it has a certain generality. It can be hopefully used in many other optical systems, such as cavity quantum electrodynamics, where ultrashort cavity plays a central role.-
Keywords:
- Schrödinger cat state /
- squeezed state /
- filter cavity /
- Gouy phase shift
[1] Yurke B, Stoler D 1986 Phys. Rev. Lett. 57 13
Google Scholar
[2] Shang S, Caves C M, Yurke B 1990 Phys. Rev. A 41 5261
Google Scholar
[3] Dakna M, Anhut T, Opatrny T, Knoll L, Welsch D G 1997 Phys. Rev. A 55 3184
Google Scholar
[4] Wenger J, Tualle-Brouri R, Grangier P 2004 Phys. Rev. Lett. 92 153601
Google Scholar
[5] Ourjoumtsev A, Tualle-Brouri R, Laurat J, Grangier P 2006 Science 312 83
Google Scholar
[6] Neergaard-Nielsen J S, Nielsen B M, Hettich C, Mølmer K, Polzik E S 2006 Phys. Rev. Lett. 97 083604
Google Scholar
[7] Wakui K, Takahashi H, Furusawa A, Sasaki M 2007 Opt. Express 15 3568
Google Scholar
[8] Ourjoumtsev A, Jeong H, Tualle-Brouri R, Grangier P 2007 Nature 448 784
Google Scholar
[9] Takahashi H, Wakui K, Suzuki S, Takeoka M, Hayasaka K, Furusawa A, Sasaki M 2008 Phys. Rev. Lett. 101 233605
Google Scholar
[10] Dong R F, Tipsmark A, Laghaout A, Krivitsky L A, Ježek M, Andersen U L 2014 J. Opt. Soc. Am. B 31 1192
Google Scholar
[11] 张娜娜, 李淑静, 闫红梅, 何亚亚, 王海 2018 67 234203
Google Scholar
Zhang N N, Li S J, Yan H M, He Y Y, Wang H 2018 Acta Phys. Sin. 67 234203
Google Scholar
[12] 何亚亚, 邓琦琦, 李淑静, 徐忠孝, 王海 2019 量子光学学报 25 372
He Y Y, Deng Q Q, Li S J, Xu Z X, Wang H 2019 Journal of Quantum Optics 25 372
[13] 王美红 2018 博士学位论文(太原: 山西大学)
Wang M H 2018 Ph. D. Dissertation (Taiyuan: Shanxi University) (in Chinese)
[14] Yoshikawa J, Asavanant W, Furusawa A 2017 Phys. Rev. A 96 052304
Google Scholar
[15] Suzuki S, Takeoka M, Sasaki M, Andersen U L, Kannari F 2006 Phys. Rev. A 73 042304
Google Scholar
[16] Asavanant W, Nakashima K, Shiozawa Y, Yoshikawa J, Furusawa A 2017 Opt. Express 25 32227
Google Scholar
[17] DeVoe R G, Fabre C, Jungmann K, Hoffnagle J, Brewer R G 1988 Phys. Rev. A 37 1802(R)
Google Scholar
[18] Lichten W 1985 J. Opt. Soc. Am. A 2 1869
Google Scholar
[19] Layer H P, Deslattes R D, Schewietzer W G 1976 Appl. Opt. 15 734
Google Scholar
[20] Hood C J, Kimble H J, Ye J 2001 Phys. Rev. A 64 033804
Google Scholar
[21] 杜金锦, 李文芳, 文瑞娟, 李刚, 张天才 2013 62 194203
Google Scholar
Du J J, Li W F, Wen R J, Gang L, Zhang T C 2013 Acta Phys. Sin. 62 194203
Google Scholar
[22] Zhang P F, Zhang Y C, Li G, Du J J, Zhang Y F, Guo Y Q, Wang J M, Zhang T C, Li W D 2011 Chin. Phys. Lett. 28 044203
Google Scholar
[23] Boca A, Miller R, Birnbaum K M, Boozer A D, McKeever J, Kimble H J 2004 Phys. Rev. Lett. 93 233603
Google Scholar
-
图 1 OPO输出的压缩光谱线(红色), 以及滤波腔(绿色)和干涉滤波片(蓝色)的透射谱线(横轴是光频率
$\nu $ 与压缩光中心频率${\nu _0}$ 的差, 单位是OPO的自由光谱范围ΔνFSR,OPO)Figure 1. Spectrum of squeezing from OPO (red), and transmission spectra of filter cavity (green) and interference filter (blue). Horizontal axis is difference of optical frequency and central frequency of squeezing, the unit is ΔνFSR,OPO.
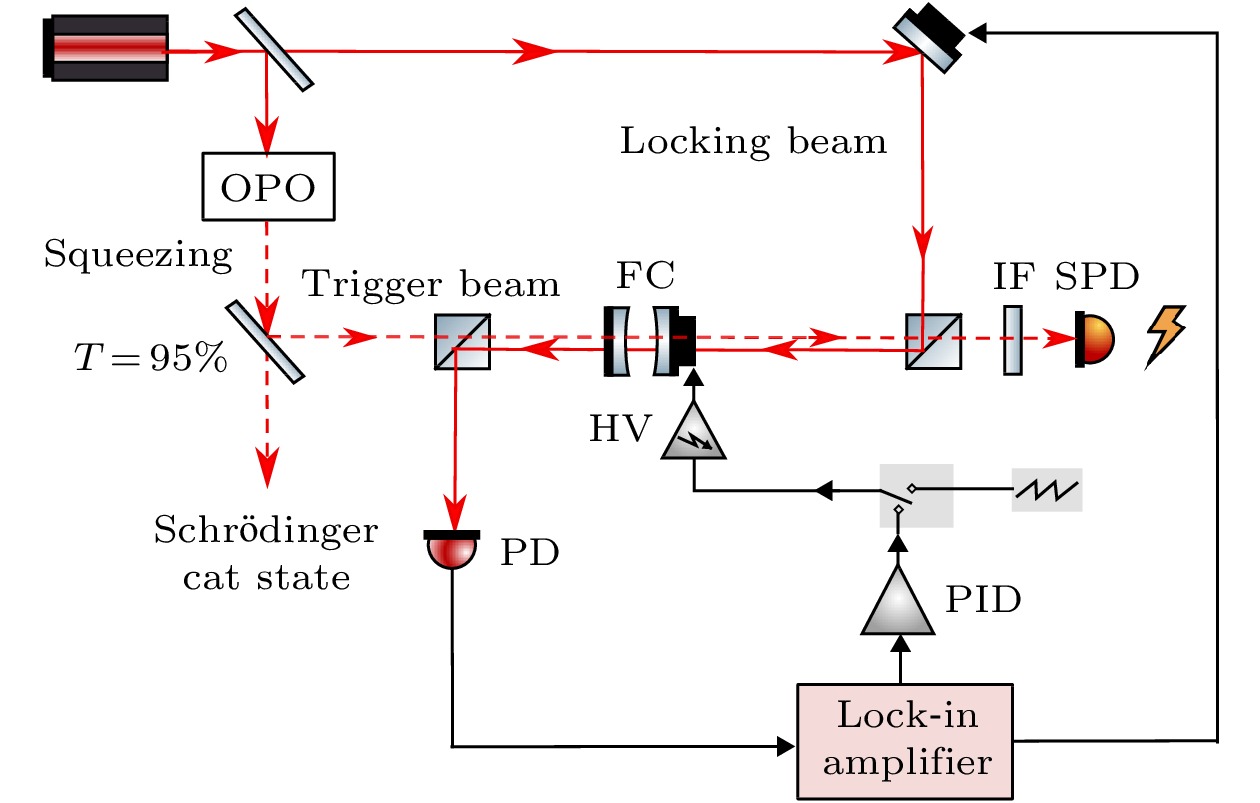
图 2 实验装置图(OPO, 光学参量振荡器; FC, 滤波腔; HV, 高压放大器; PD, 光探测器; IF, 干涉滤波片; SPD, 单光子探测器; PID, 比例积分微分控制器; lock-in amplifier, 锁相放大器)
Figure 2. Experimental setup of Schrödinger cat. OPO, optical parametric oscillator; FC, filter cavity; PD, photon detector; SPD, single-photon detector; PID, proportional-integral-differential amplifier.
图 3 光探测器探测到的滤波腔透射光强(绿色曲线)和腔扫描电压(蓝色曲线) (a)在同一个扫描方向上扫出三个FSR; (b)将(a)中的第二个透射峰展开
Figure 3. Cavity transmission (green line) and the corresponding scanning voltage (blue line): (a) Three FSR is scanned; (b) expansion of the second transmission peak.
图 4 压电陶瓷响应曲线拟合(圆圈是实验数据, 实线是拟合曲线)
Figure 4. Fitting of Piezo response (circles correspond to experimental data, solid line is fitting curve).
-
[1] Yurke B, Stoler D 1986 Phys. Rev. Lett. 57 13
Google Scholar
[2] Shang S, Caves C M, Yurke B 1990 Phys. Rev. A 41 5261
Google Scholar
[3] Dakna M, Anhut T, Opatrny T, Knoll L, Welsch D G 1997 Phys. Rev. A 55 3184
Google Scholar
[4] Wenger J, Tualle-Brouri R, Grangier P 2004 Phys. Rev. Lett. 92 153601
Google Scholar
[5] Ourjoumtsev A, Tualle-Brouri R, Laurat J, Grangier P 2006 Science 312 83
Google Scholar
[6] Neergaard-Nielsen J S, Nielsen B M, Hettich C, Mølmer K, Polzik E S 2006 Phys. Rev. Lett. 97 083604
Google Scholar
[7] Wakui K, Takahashi H, Furusawa A, Sasaki M 2007 Opt. Express 15 3568
Google Scholar
[8] Ourjoumtsev A, Jeong H, Tualle-Brouri R, Grangier P 2007 Nature 448 784
Google Scholar
[9] Takahashi H, Wakui K, Suzuki S, Takeoka M, Hayasaka K, Furusawa A, Sasaki M 2008 Phys. Rev. Lett. 101 233605
Google Scholar
[10] Dong R F, Tipsmark A, Laghaout A, Krivitsky L A, Ježek M, Andersen U L 2014 J. Opt. Soc. Am. B 31 1192
Google Scholar
[11] 张娜娜, 李淑静, 闫红梅, 何亚亚, 王海 2018 67 234203
Google Scholar
Zhang N N, Li S J, Yan H M, He Y Y, Wang H 2018 Acta Phys. Sin. 67 234203
Google Scholar
[12] 何亚亚, 邓琦琦, 李淑静, 徐忠孝, 王海 2019 量子光学学报 25 372
He Y Y, Deng Q Q, Li S J, Xu Z X, Wang H 2019 Journal of Quantum Optics 25 372
[13] 王美红 2018 博士学位论文(太原: 山西大学)
Wang M H 2018 Ph. D. Dissertation (Taiyuan: Shanxi University) (in Chinese)
[14] Yoshikawa J, Asavanant W, Furusawa A 2017 Phys. Rev. A 96 052304
Google Scholar
[15] Suzuki S, Takeoka M, Sasaki M, Andersen U L, Kannari F 2006 Phys. Rev. A 73 042304
Google Scholar
[16] Asavanant W, Nakashima K, Shiozawa Y, Yoshikawa J, Furusawa A 2017 Opt. Express 25 32227
Google Scholar
[17] DeVoe R G, Fabre C, Jungmann K, Hoffnagle J, Brewer R G 1988 Phys. Rev. A 37 1802(R)
Google Scholar
[18] Lichten W 1985 J. Opt. Soc. Am. A 2 1869
Google Scholar
[19] Layer H P, Deslattes R D, Schewietzer W G 1976 Appl. Opt. 15 734
Google Scholar
[20] Hood C J, Kimble H J, Ye J 2001 Phys. Rev. A 64 033804
Google Scholar
[21] 杜金锦, 李文芳, 文瑞娟, 李刚, 张天才 2013 62 194203
Google Scholar
Du J J, Li W F, Wen R J, Gang L, Zhang T C 2013 Acta Phys. Sin. 62 194203
Google Scholar
[22] Zhang P F, Zhang Y C, Li G, Du J J, Zhang Y F, Guo Y Q, Wang J M, Zhang T C, Li W D 2011 Chin. Phys. Lett. 28 044203
Google Scholar
[23] Boca A, Miller R, Birnbaum K M, Boozer A D, McKeever J, Kimble H J 2004 Phys. Rev. Lett. 93 233603
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 6425
- PDF Downloads: 86
- Cited By: 0
