双模压缩态量子相干性演化的实验研究

蔚娟; 张岩; 吴银花; 杨文海; 闫智辉; 贾晓军

doi:10.7498/aps.72.20221923

摘要

量子相干性作为量子力学一个最显著的特征, 被认为是量子信息过程中很重要的一种量子资源. 单模压缩态和双模压缩态(Einstein-Podolsky-Rosen纠缠态)均具有量子相干性, 在制备和传输过程中的量子相干性对于实际应用具有重要意义. 利用平衡零拍探测重构量子态的协方差矩阵, 本文定量分析了量子态制备过程中的不完美以及信道传输损耗对单模和双模压缩态量子相干性的影响. 实验证明量子态的压缩和纠缠特性及量子相干性对损耗均是鲁棒的. 特别地, 压缩和纠缠特性会随着量子态制备过程中热光子数的增大而减小, 直至消失, 而当压缩和纠缠均已消失时, 量子相干性依然存在. 实验结果为压缩态、纠缠态光场的量子相干性作为量子资源在量子信息过程中的应用提供了参考.

关键词:

Abstract

As one of the most remarkable features of quantum mechanics, quantum coherence is regarded as an important quantum resource in the quantum information processing. The one-mode squeezed state and the two-mode squeezed state (Einstein-Podolsky-Rosen (EPR) entangled states) as the most representative examples of nonclassical states both have quantum coherence. The squeezing property of the squeezed state is described by the variance of quadrature components, and the positive partial transposition (PPT) criterion is used to describe the entanglement of the EPR entangled states. The research of the quantum coherence of Gaussian states is also a bridge between the properties of squeezing and entanglement. It has been shown that the quantum coherence with infinite-dimensional systems can be quantified by relative entropy. One of the widely used effective methods to obtain the value of quantum coherence experimentally is the quantum tomography. The covariance matrices of the quantum states are reconstructed via balanced homodyne detection and then taken into quantum coherence expression to calculate the corresponding value. The main factors affecting quantum coherence are the classical and uncorrelated noise in the actual experimental generation processing and the decoherence effect caused by the coupling between quantum resources and the surrounding environment. And the quantum coherence evolution in the generation and transmission process of the quantum resources is essential for the practical applications. Therefore, we analyze in detail the influences of the impurity of quantum resource on squeezing, entanglement and quantum coherence. The evolutions of quantum coherence of these Gaussian states in the lossy channels are demonstrated experimentally. The quantum coherence is shown to be robust against the loss in the lossy channels, which is similar to the case of squeezing and entanglement. The quantum coherences of the squeezed states and the EPR entangled states are robust against the thermal photons in the actual experimental generation processing, although the squeezing and entanglement of Gaussian states disappear at a certain number of thermal photons. Our research results provide a reference for the practical applications of quantum coherence of the squeezed state and entangled states in the lossy environment.

Keywords:

squeezed state /
Einstein-Podolsky-Rosen entangled states /
purity of quantum state /
quantum coherence

作者及机构信息

1.
西安工业大学光电工程学院, 西安　710021

2.
山西大学光电研究所, 量子光学与光量子器件国家重点实验室, 太原　030006

3.
山西大学, 极端光学协同创新中心, 太原　030006

4.
中国空间技术研究院西安分院, 西安　710000

通信作者: 蔚娟, yujuan643@126.com

基金项目: 国家自然科学基金(批准号: 62105256, 62122044, 61925503, 11904218, 12147215, 11834010, 62135008, 62001374, 12004276, 12103039)、陕西省教育厅自然科学研究项目(批准号: 21JK0694, 18JK0386, 21JY016)、山西省高等学校创新人才支持计划、山西省高等学校科技创新项目(批准号: 2019L0794)、山西青年三晋学者项目、山西省“1331 工程”重点学科建设计划资助的课题和陕西省自然科学基础研究项目(批准号: 2021JQ-640)资助的课题.

Authors and contacts

1.
School of Optoelectronic Engineering, Xi’an Technological University, Xi’an 710021, China

2.
State Key Laboratory of Quantum Optics and Quantum Optics Devices, Institute of Opto-Electronics, Shanxi University, Taiyuan 030006, China

3.
Collaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan 030006, China

4.
China Academy of Space Technology (Xi’an), Xi’an 710000, China

Corresponding author: Yu Juan, yujuan643@126.com

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 62105256, 62122044, 61925503, 11904218, 12147215, 11834010, 62135008, 62001374, 12004276, 12103039), the Natural Science Research Program of the Education Department of Shaanxi Province, China (Grant Nos. 21JK0694, 18JK0386, 21JY016), the Program for the Innovative Talents of Higher Education Institutions of Shanxi, China, the Scientific and Technological Programs of Higher Education Institutions in Shanxi, China (Grant No. 2019L0794), the Program for Sanjin Scholars of Shanxi Province, China, the Fund for Shanxi “1331Project” Key Subjects Construction, China, and the Natural Science Basic Research Program in Shaanxi Province of China (Grant No. 2021JQ-640).

文章全文 : translate this paragraph

参考文献

[1]	Baumgratz T, Cramer M, Plenio M B 2014 Phys. Rev. Lett. 113 140401 Google Scholar
[2]	Li Y C, Lin H Q 2016 Sci. Rep. 6 26365 Google Scholar
[3]	Shi Y H, Shi H L, Wang X H, Hu M L, Liu S Y, Yang W L, Fan H 2020 J. Phys. A 53 085301 Google Scholar
[4]	Hillery M 2016 Phys. Rev. A 93 012111 Google Scholar
[5]	Napoli C, Bromley T R, Cianciaruso M, Piani M, Johnston N, Adesso G 2016 Phys. Rev. Lett. 116 150502 Google Scholar
[6]	Gisin N, Ribordy G, Tittel W, Zbinden H 2002 Rev. Mod. Phys. 74 145 Google Scholar
[7]	Giovannetti V, Lloyd S, Maccone L 2011 Nat. Photonics 5 222 Google Scholar
[8]	Giorda P, Allegra M 2016 J Phys. A-Math. Theor. 51 2 Google Scholar
[9]	Zhang A, Zhang K, Zhou L, ZhangW 2018 Phys. Rev. Lett. 121 073602 Google Scholar
[10]	Yuan Y, Hou Z, Zhao Y Y, Zhong H S, Xiang G Y, Li C F, Guo G C 2018 Opt. Express 26 004470 Google Scholar
[11]	Wu K D, Hou Z, Zhong H S, Yuan Y, Guo G C 2017 Optica 4 454 Google Scholar
[12]	Zhang M, Kang H J, Wang M H, Xu X L, Peng K C 2021 Photonics Res. 9 887 Google Scholar
[13]	Tan K C, Volkoff T, Kwon H, Jeong H 2017 Phys. Rev. Lett. 119 190405 Google Scholar
[14]	Tan K C, Jeong H 2018 Phys. Rev. Lett. 121 220401 Google Scholar
[15]	Lostaglio M, Müller M P 2019 Phys. Rev. Lett. 123 020403 Google Scholar
[16]	林银, 黄明达, 於亚飞, 张智明 2017 66 110301 Google Scholar Lin Y, Huang M D, Yu Y F, Zhang Z M 2017 Acta Phys. Sin. 66 110301 Google Scholar
[17]	Braunstein S L, Caves C M 1994 Phys. Rev. Lett. 72 3439 Google Scholar
[18]	Feng X N, Wei L F 2017 Sci. Rep. 7 15492 Google Scholar
[19]	Zhang Y R, Shao L H, Li Y, Fan H 2016 Phys. Rev. A 93 012334 Google Scholar
[20]	Xu J 2016 Phys. Rev. A 93 032111 Google Scholar
[21]	Buono D, Buono G, Petrillo G, Torre G, Zonzo G, Illuminati F 2016 arXiv: 1609.00913
[22]	周瑶瑶, 刘艳红, 闫智辉, 贾晓军 2021 70 104203 Google Scholar Zhou Y Y, Liu Y H 2021 Acta Phys. Sin. 70 104203 Google Scholar
[23]	Yan Z H, Qin J, Qin Z Z, Su X L, Jia X J, Xie C D, Peng K C 2021 Fundamental Research 1 43 Google Scholar
[24]	Chou C W, Hume D B, Thorpe M J, Wineland D J, Rosenband T 2011 Phys. Rev. Lett. 106 160801 Google Scholar
[25]	Huo M R, Qin J L, Cheng J L, Yan Z H, Qin Z Z, Su X L, Jia X J, Xie C D, Peng K C 2018 Sci. Adv. 4 eaas9401 Google Scholar
[26]	Liu S S, Lou Y B, Chen Y X, Jing J T 2022 Phys. Rev. Lett. 128 060503 Google Scholar
[27]	Yan Z H, Wu L, Jia X J, Liu Y H, Deng R J, Li S J, Wang H, Xie C D, Peng K C 2017 Nat. Commun. 8 718 Google Scholar
[28]	Ma L X, Lei X, Yan J L, Li R Y, Chai T, Yan Z H, Jia X J, Xie C D, Peng K C 2022 Nat. Commun. 13 2368 Google Scholar
[29]	Lei X, Ma L X, Yan J L, Zhou X Y, Yan Z H, Jia X J 2022 Adv. Phys. X 7 2060133 Google Scholar
[30]	Liu S S, Lou Y B, Xin J, Jing J T 2018 Phys. Rev. Appl. 10 064046 Google Scholar
[31]	Liu Y H, Huo N, Li J M, Cui L, Li X Y, Ou Z Y 2019 Opt. Express 27 11292 Google Scholar
[32]	Yu J, Qin Y, Qin J L, Wang H, Yan Z H, Jia X J, Peng K C 2020 Phys. Rev. Appl. 13 024037 Google Scholar
[33]	Goda K, Miyakawa O, Mikhailov E E, Saraf S, Adhikari R, McKenzie K, Ward R, Vass S, Weinstein A J, Mavalvala N 2008 Nat. Phys. 4 472 Google Scholar
[34]	Guo X S, Breum C R, Borregaard J, Izumi S, Larsen M V, Gehring T, Christandl M, Neergaard-Nielsen J S, Andersen U L 2020 Nat. Phys. 16 281 Google Scholar
[35]	Bai S Y, An J H 2021 Phys. Rev. Lett. 127 083602 Google Scholar
[36]	Yan Z H, Wu L, Jia X J, Xie C D, Peng K C 2021 Adv. Quantum Technol. 4 2100071 Google Scholar
[37]	Streltsov A, Singh U, Dhar H S, Bera M N, Adesso G 2015 Phys. Rev. Lett. 115 020403 Google Scholar
[38]	Chitambar E, Hsieh M H 2016 Phys. Rev. Lett. 117 020402 Google Scholar
[39]	Deng X W, Liu Y, Wang M H, Su X L, Peng K C 2021 npj Quantum Inform. 7 65 Google Scholar
[40]	Liu Y, Zheng K M, Kang H J, Han D M, Wang M H, Zhang L J, Su X L, Peng K C 2022 npj Quantum Inform. 8 38 Google Scholar
[41]	Kang H J, Han D M, Wang N, Liu Y, Hao S H, Su X L 2021 Photonics Res. 9 1330 Google Scholar
[42]	Weedbrook C, Pirandola S, García-Patrón R, Cerf N J, Ralph T C, Shapiro J H, Lloyd S 2012 Rev. Mod. Phys. 84 621 Google Scholar
[43]	Takeno Y, Yukawa M, Yonezawa H, Furusawa A 2007 Opt. Express 15 4321 Google Scholar
[44]	Adesso G, Serafini A 2004 Phys. Rev. A 70 022318 Google Scholar
[45]	Ou Z Y, Pereira S F, Kimble H J, Peng K C 1992 Phys. Rev. Lett. 68 3663 Google Scholar
[46]	Zhou Y Y, Yu J, Yan Z H, Jia X J, Zhang J, Xie C D, Peng K C 2018 Phys. Rev. Lett. 121 150502 Google Scholar
[47]	Bougouffa S, Ficek Z 2020 Phys. Rev. A 102 043720 Google Scholar
[48]	Xiong S J, Sun Z, Su Q P, Xi Z J, Yang C P 2021 Optica 8 1003 Google Scholar

施引文献

图 1 实验装置示意图, 其中DBS为双色分束镜; MC为模式清洁器; HWP为半波片; HR为高反镜; PBS为偏振分光棱镜; LO为本地振荡光

Fig. 1. Schematic diagram of experimental setup. DBS, dichroic beam splitter; MC, mode cleaner; HWP, half-wave plate; HR, high reflection; PBS, polarizing beam splitter; LO, a strong local oscillator beam.

下载: 全尺寸图片幻灯片

图 2 单模压缩态压缩特性和量子相干性随热光子数的变化　(a) 相对噪声功率; (b) 量子相干性

Fig. 2. Dependence of squeezing level and quantum coherence of the one-mode squeezed state on the number of thermal photons: (a) Relative noise power; (b) quantum coherence.

下载: 全尺寸图片幻灯片

图 3 单模压缩态实验结果　(a) 相对噪声功率随传输效率的变化; (b) 损耗信道中压缩态光场的纯度对量子相干性的影响

Fig. 3. Experimental results of the one-mode squeezed state in a lossy channel: (a) Dependence of relative noise power on the transmission efficiency; (b) the influence of purity of squeezed state on quantum coherence in a lossy channel.

下载: 全尺寸图片幻灯片

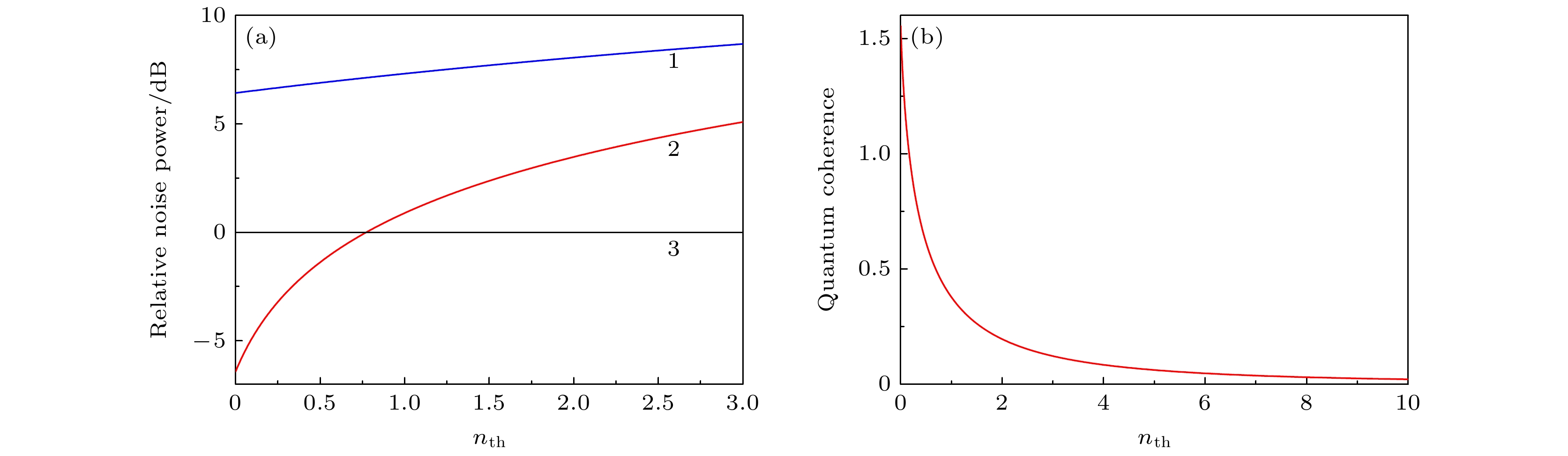
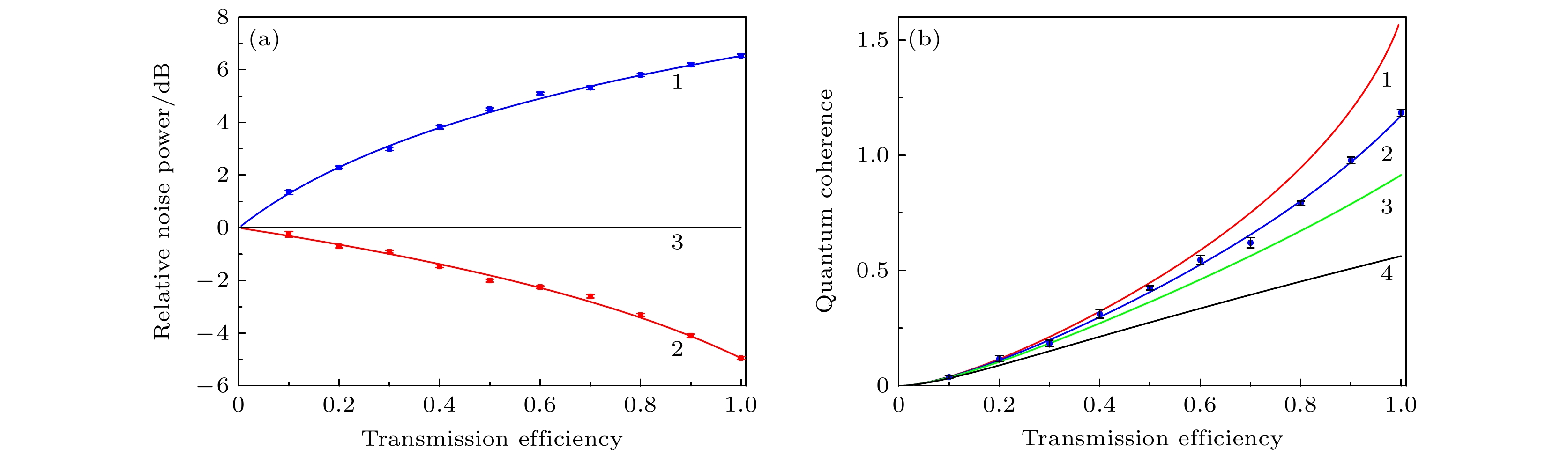
图 4 双模压缩态实验结果　(a) PPT值随热光子数的变化; (b) 量子相干性随热光子数的变化; (c) 纠缠特性随传输效率的变化; (d) 量子相干性随传输效率的变化

Fig. 4. Experimental results of the two-mode squeezed states in lossy channels: (a) Dependence of PPT value on the number of thermal photons; (b) dependence of quantum coherence on the number of thermal photons; (c) dependence of PPT values on the transmission efficiency; (d) decoherence of quantum coherence in the lossy channels.

下载: 全尺寸图片幻灯片

map

[1]	Baumgratz T, Cramer M, Plenio M B 2014 Phys. Rev. Lett. 113 140401 Google Scholar
[2]	Li Y C, Lin H Q 2016 Sci. Rep. 6 26365 Google Scholar
[3]	Shi Y H, Shi H L, Wang X H, Hu M L, Liu S Y, Yang W L, Fan H 2020 J. Phys. A 53 085301 Google Scholar
[4]	Hillery M 2016 Phys. Rev. A 93 012111 Google Scholar
[5]	Napoli C, Bromley T R, Cianciaruso M, Piani M, Johnston N, Adesso G 2016 Phys. Rev. Lett. 116 150502 Google Scholar
[6]	Gisin N, Ribordy G, Tittel W, Zbinden H 2002 Rev. Mod. Phys. 74 145 Google Scholar
[7]	Giovannetti V, Lloyd S, Maccone L 2011 Nat. Photonics 5 222 Google Scholar
[8]	Giorda P, Allegra M 2016 J Phys. A-Math. Theor. 51 2 Google Scholar
[9]	Zhang A, Zhang K, Zhou L, ZhangW 2018 Phys. Rev. Lett. 121 073602 Google Scholar
[10]	Yuan Y, Hou Z, Zhao Y Y, Zhong H S, Xiang G Y, Li C F, Guo G C 2018 Opt. Express 26 004470 Google Scholar
[11]	Wu K D, Hou Z, Zhong H S, Yuan Y, Guo G C 2017 Optica 4 454 Google Scholar
[12]	Zhang M, Kang H J, Wang M H, Xu X L, Peng K C 2021 Photonics Res. 9 887 Google Scholar
[13]	Tan K C, Volkoff T, Kwon H, Jeong H 2017 Phys. Rev. Lett. 119 190405 Google Scholar
[14]	Tan K C, Jeong H 2018 Phys. Rev. Lett. 121 220401 Google Scholar
[15]	Lostaglio M, Müller M P 2019 Phys. Rev. Lett. 123 020403 Google Scholar
[16]	林银, 黄明达, 於亚飞, 张智明 2017 66 110301 Google Scholar Lin Y, Huang M D, Yu Y F, Zhang Z M 2017 Acta Phys. Sin. 66 110301 Google Scholar
[17]	Braunstein S L, Caves C M 1994 Phys. Rev. Lett. 72 3439 Google Scholar
[18]	Feng X N, Wei L F 2017 Sci. Rep. 7 15492 Google Scholar
[19]	Zhang Y R, Shao L H, Li Y, Fan H 2016 Phys. Rev. A 93 012334 Google Scholar
[20]	Xu J 2016 Phys. Rev. A 93 032111 Google Scholar
[21]	Buono D, Buono G, Petrillo G, Torre G, Zonzo G, Illuminati F 2016 arXiv: 1609.00913
[22]	周瑶瑶, 刘艳红, 闫智辉, 贾晓军 2021 70 104203 Google Scholar Zhou Y Y, Liu Y H 2021 Acta Phys. Sin. 70 104203 Google Scholar
[23]	Yan Z H, Qin J, Qin Z Z, Su X L, Jia X J, Xie C D, Peng K C 2021 Fundamental Research 1 43 Google Scholar
[24]	Chou C W, Hume D B, Thorpe M J, Wineland D J, Rosenband T 2011 Phys. Rev. Lett. 106 160801 Google Scholar
[25]	Huo M R, Qin J L, Cheng J L, Yan Z H, Qin Z Z, Su X L, Jia X J, Xie C D, Peng K C 2018 Sci. Adv. 4 eaas9401 Google Scholar
[26]	Liu S S, Lou Y B, Chen Y X, Jing J T 2022 Phys. Rev. Lett. 128 060503 Google Scholar
[27]	Yan Z H, Wu L, Jia X J, Liu Y H, Deng R J, Li S J, Wang H, Xie C D, Peng K C 2017 Nat. Commun. 8 718 Google Scholar
[28]	Ma L X, Lei X, Yan J L, Li R Y, Chai T, Yan Z H, Jia X J, Xie C D, Peng K C 2022 Nat. Commun. 13 2368 Google Scholar
[29]	Lei X, Ma L X, Yan J L, Zhou X Y, Yan Z H, Jia X J 2022 Adv. Phys. X 7 2060133 Google Scholar
[30]	Liu S S, Lou Y B, Xin J, Jing J T 2018 Phys. Rev. Appl. 10 064046 Google Scholar
[31]	Liu Y H, Huo N, Li J M, Cui L, Li X Y, Ou Z Y 2019 Opt. Express 27 11292 Google Scholar
[32]	Yu J, Qin Y, Qin J L, Wang H, Yan Z H, Jia X J, Peng K C 2020 Phys. Rev. Appl. 13 024037 Google Scholar
[33]	Goda K, Miyakawa O, Mikhailov E E, Saraf S, Adhikari R, McKenzie K, Ward R, Vass S, Weinstein A J, Mavalvala N 2008 Nat. Phys. 4 472 Google Scholar
[34]	Guo X S, Breum C R, Borregaard J, Izumi S, Larsen M V, Gehring T, Christandl M, Neergaard-Nielsen J S, Andersen U L 2020 Nat. Phys. 16 281 Google Scholar
[35]	Bai S Y, An J H 2021 Phys. Rev. Lett. 127 083602 Google Scholar
[36]	Yan Z H, Wu L, Jia X J, Xie C D, Peng K C 2021 Adv. Quantum Technol. 4 2100071 Google Scholar
[37]	Streltsov A, Singh U, Dhar H S, Bera M N, Adesso G 2015 Phys. Rev. Lett. 115 020403 Google Scholar
[38]	Chitambar E, Hsieh M H 2016 Phys. Rev. Lett. 117 020402 Google Scholar
[39]	Deng X W, Liu Y, Wang M H, Su X L, Peng K C 2021 npj Quantum Inform. 7 65 Google Scholar
[40]	Liu Y, Zheng K M, Kang H J, Han D M, Wang M H, Zhang L J, Su X L, Peng K C 2022 npj Quantum Inform. 8 38 Google Scholar
[41]	Kang H J, Han D M, Wang N, Liu Y, Hao S H, Su X L 2021 Photonics Res. 9 1330 Google Scholar
[42]	Weedbrook C, Pirandola S, García-Patrón R, Cerf N J, Ralph T C, Shapiro J H, Lloyd S 2012 Rev. Mod. Phys. 84 621 Google Scholar
[43]	Takeno Y, Yukawa M, Yonezawa H, Furusawa A 2007 Opt. Express 15 4321 Google Scholar
[44]	Adesso G, Serafini A 2004 Phys. Rev. A 70 022318 Google Scholar
[45]	Ou Z Y, Pereira S F, Kimble H J, Peng K C 1992 Phys. Rev. Lett. 68 3663 Google Scholar
[46]	Zhou Y Y, Yu J, Yan Z H, Jia X J, Zhang J, Xie C D, Peng K C 2018 Phys. Rev. Lett. 121 150502 Google Scholar
[47]	Bougouffa S, Ficek Z 2020 Phys. Rev. A 102 043720 Google Scholar
[48]	Xiong S J, Sun Z, Su Q P, Xi Z J, Yang C P 2021 Optica 8 1003 Google Scholar

[1]	王渝, 吴艺豪, 李易璞, 卢凯翔, 伊天成, 张云波. 二维旋转谐振子势中单粒子的跳频压缩及演化. , 2024, 73(7): 074202. doi: 10.7498/aps.73.20231929
[2]	赵豪, 冯晋霞, 孙婧可, 李渊骥, 张宽收. 连续变量Einstein-Podolsky-Rosen纠缠态光场在光纤信道中分发时纠缠的鲁棒性. , 2022, 71(9): 094202. doi: 10.7498/aps.71.20212380
[3]	董曜, 纪爱玲, 张国锋. 关联退极化量子信道中qutrit-qutrit系统的量子相干性演化. , 2022, 71(7): 070303. doi: 10.7498/aps.71.20212067
[4]	翟泽辉, 郝温静, 刘建丽, 段西亚. 用于光学薛定谔猫态制备的滤波设计与滤波腔腔长测量. , 2020, 69(18): 184204. doi: 10.7498/aps.69.20200589
[5]	田聪, 鹿翔, 张英杰, 夏云杰. 纠缠相干光场对量子态最大演化速率的操控. , 2019, 68(15): 150301. doi: 10.7498/aps.68.20190385
[6]	左小杰, 孙颍榕, 闫智辉, 贾晓军. 高灵敏度的量子迈克耳孙干涉仪. , 2018, 67(13): 134202. doi: 10.7498/aps.67.20172563
[7]	伊天成, 丁悦然, 任杰, 王艺敏, 尤文龙. 具有Dzyaloshinskii-Moriya相互作用的XY模型的量子相干性. , 2018, 67(14): 140303. doi: 10.7498/aps.67.20172755
[8]	叶世强, 陈小余. 基于量子相干性的四体贝尔不等式构建. , 2017, 66(20): 200301. doi: 10.7498/aps.66.200301
[9]	杨丽君, 马腾, 孙克家, 冯晓敏. 微波场作用下三能级原子系统的无反转光放大. , 2015, 64(6): 064205. doi: 10.7498/aps.64.064205
[10]	余学才, 汪平和, 张利勋. 光晶格动量依赖偶极势中原子运动. , 2013, 62(14): 144202. doi: 10.7498/aps.62.144202
[11]	李巍, 王永钢, 杨伯君. 损耗对表面等离子体激元压缩态的影响. , 2011, 60(2): 024203. doi: 10.7498/aps.60.024203
[12]	马瑞琼, 李永放, 时坚. 量子态的非相干光时域测量. , 2008, 57(9): 5593-5599. doi: 10.7498/aps.57.5593
[13]	张淼, 贾焕玉, 姬晓辉, 司坤, 韦联福. 制备囚禁冷离子的振动压缩量子态. , 2008, 57(12): 7650-7657. doi: 10.7498/aps.57.7650
[14]	胡菊菊, 蔡十华, 王建秋, 嵇英华. 声子库的量子态对介观电路量子特性影响的研究. , 2008, 57(1): 496-501. doi: 10.7498/aps.57.496
[15]	张婉娟, 王治国, 谢双媛, 羊亚平. 频率变化的压缩态光场与原子的相互作用. , 2007, 56(4): 2168-2174. doi: 10.7498/aps.56.2168
[16]	金硕, 解炳昊. 外磁场中海森伯反铁磁模型的代数结构和压缩态解. , 2006, 55(8): 3880-3884. doi: 10.7498/aps.55.3880
[17]	贾晓军, 苏晓龙, 潘庆, 谢常德, 彭堃墀. 具有经典相干性的两组EPR纠缠态光场的实验产生. , 2005, 54(6): 2717-2722. doi: 10.7498/aps.54.2717
[18]	宋同强. 利用双模压缩真空态实现量子态的远程传输. , 2004, 53(10): 3358-3362. doi: 10.7498/aps.53.3358
[19]	邓文基, 许运华, 刘平. 测不准关系和最小不确定态. , 2003, 52(12): 2961-2964. doi: 10.7498/aps.52.2961
[20]	郝三如, 王麓雅. 用外加驱动场压缩有热槽相互作用二态量子系统的退相干性. , 2000, 49(4): 610-614. doi: 10.7498/aps.49.610

计量

文章访问数: 4779
PDF下载量: 169
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

双模压缩态量子相干性演化的实验研究