-
本文主要研究二维旋转谐振子势中单粒子的动力学行为, 通过跳频的方式分析该粒子的压缩演化过程, 并分析了相应的物理机制. 一方面, 研究跳频过程对回旋半径模式的压缩演化, 通过选择适当的跳频时刻, 分析跳频过程对压缩的影响. 研究表明, 回旋半径坐标的压缩程度并未在跳频时刻发生改变, 但可在后续的演化中出现更强的压缩现象. 另一方面, 主要研究跳频过程中心导向模式的压缩演化. 通过参数的选择, 分析了两种压缩模式, 即发散模式和振荡模式的压缩及演化. 有趣的是, 在中心导向模式压缩中, 外势存在一个由旋转角速度决定的临界势阱纵横比. 压缩模式在此处发生突变, 且在振荡模式中, 势阱纵横比趋于该临界值时, 将出现明显的压缩.The control of microscopic particle behavior based on a specific external field has always been a research hotspot in the field of physics. Many studies have been exploring various methods to manipulate and control the behavior of particles at a microscopic level. In this work, we investigate the phenomenon of single-particle squeezing induced by frequency jumping in a two-dimensional rotating harmonic oscillator potential. Squeezing, as a quantum mechanical phenomenon, has attracted significant attention due to its potential applications in various fields. It refers to the reduction of fluctuations in certain physical quantities, allowing for more precise measurement results. Squeezing phenomena have been extensively studied in different physical systems, including optics, atomic physics, and solid-state physics. However, there have been few reports on the quantum state squeezing phenomenon induced by frequency jumping in a rotating harmonic oscillator potential. Therefore, our study aims to fill this gap and shed light on this intriguing phenomenon. To explore the squeezing phenomenon induced by frequency jumping, we focus on the fluctuations and squeezing of the single particle’s cyclotron radius coordinate and center-guided coordinate in the two-dimensional rotating harmonic oscillator potential. Through numerical simulations and theoretical analysis, we can understand the influence of frequency jumping on the degree of squeezing and reveal the underlying physical mechanism of squeezing evolution. In this work, we first investigate the influence of frequency jumping on the squeezing evolution of the cyclotron radius mode. By carefully selecting appropriate jumping moments, we analyze the influence of frequency jumping on the degree of squeezing. Our research results show that the degree of squeezing in the cyclotron radius coordinate remains unchanged at the jumping moment. However, we observe a stronger squeezing phenomenon in the subsequent evolution process. This indicates that frequency jumping plays a crucial role in squeezing evolution of the cyclotron radius mode. Furthermore, we focus on the squeezing evolution of the center-guided mode during frequency jumping. By selecting suitable parameters, we analyze the squeezing and evolution of two squeezing modes: the divergent mode and the oscillatory mode. Interestingly, we discover the existence of a critical potential trap aspect ratio, which is determined by the rotation angular velocity of the external potential. When the aspect ratio approaches this critical value, the squeezing mode undergoes a transition, and a significant squeezing phenomenon appears in the oscillatory mode. This finding provides valuable insights into the origin and control of squeezing phenomena. Finally, we discuss the potential applications of these squeezing phenomena. Squeezing has significant implications in the fields of quantum sensing and quantum information processing. Through a deeper understanding of the squeezing evolution process caused by frequency jump, we can better control the microscopic particle behavior through external field. This knowledge opens up new possibilities for future physical research and technical applications.
-
Keywords:
- frequency jumping /
- squeezed state /
- harmonic oscillator potential
[1] Burd S C, Srinivas R, Bollinger J J, Wilson A C, Wineland D J, Leibfried D, Slichter D H, Allcock D T C 2019 Science 364 1163
Google Scholar
[2] Fletcher R J, A Shaffer, Wilson C C, Patel P B, Yan Z, Crépel V, Mukherjee B, Zwierlein M W 2021 Science 372 1318
Google Scholar
[3] Sharma V, Mueller E J 2022 Phys. Rev. A 105 023310
Google Scholar
[4] Hu J, Chen W, Vendeiro Z, Urvoy A, Braverman B, Vuletić V 2017 Phys. Rev. A 96 050301
Google Scholar
[5] Shankar A, Tang Chen, Affolter M, Gilmore K, Dubin D H E, Parker S, Holland M J, Bollinger J J 2020 Phys. Rev. A 102 053106
Google Scholar
[6] Maslowski T, Sedlmayr N 2023 Phys. Rev. B 108 094306
Google Scholar
[7] Yuen H P 1976 Phys. Rev. A 13 2226
Google Scholar
[8] Slusher R E, Hollberg L W, Yurke B, Mertz J C, Valley J F 1985 Phys. Rev. Lett. 55 2409
Google Scholar
[9] Hosten O, Engelsen N J, Krishnakumar R, Kasevich M A 2016 Nature 529 505
Google Scholar
[10] Wollman E E, Lei C U, Weinstein A J, Suh J, Kronwald A, Marquardt F, Clerk A A, Schwab K C 2015 Science 349 952
Google Scholar
[11] Lecocq F, Clark J B, Simmonds R W, Aumentado J, Teufel J D 2015 Phys. Rev. X 5 041037
Google Scholar
[12] Pirkkalainen J M, Damskägg E, Brandt M, Massel F, Sillanpää M A 2015 Phys. Rev. Lett. 115 243601
Google Scholar
[13] Meekhof D M, Monroe C, E King B, M Itano W, Wineland D J 1996 Phys. Rev. Lett. 76 1796
Google Scholar
[14] Kienzler D, Lo H Y, Keitch B, de Clercq L, Leupold F, Lindenfelser F, Marinelli M, Negnevitsky V, Home J P 2015 Science 347 53
Google Scholar
[15] Meylahn F, Willke B, Vahlbruch H 2022 Phys. Rev. Lett. 129 121103
Google Scholar
[16] Pezzè L, Smerzi A 2020 Phys. Rev. Lett. 125 210503
Google Scholar
[17] Li T, Wang W, Yi X 2021 Phys. Rev. A 104 013521
Google Scholar
[18] Yurke B, McCall S L, Klauder J R 1986 Phys. Rev. A 33 4033
Google Scholar
[19] Davis E, Bentsen G, Schleier-Smith M 2016 Phys. Rev. Lett. 116 053601
Google Scholar
[20] Linnemann D, Strobel H, Muessel W, Schulz J, Lewis-Swan R J, Kheruntsyan K V, Oberthaler M K 2016 Phys. Rev. Lett. 117 013001
Google Scholar
[21] Malnou M, Palken D A, Brubaker B M, Vale Leila R, Hilton Gene C, Lehnert K W 2019 Phys. Rev. X 9 021023
Google Scholar
[22] Eddins A, Schreppler S, Toyli D M, Martin L S, Hacohen-Gourgy S, Govia L C G, Ribeiro H, Clerk A A, Siddiqi I 2018 Phys. Rev. Lett. 120 040505
Google Scholar
[23] Janszky J, Yushin Y Y 1986 Opt. Commun. 59 151
Google Scholar
[24] Schleich W, Wheeler J A 1987 Nature 326 574
Google Scholar
[25] Graham R 1987 J. Mod. Opt. 34 873
Google Scholar
[26] Ma X, Rhodes W 1989 Phys. Rev. A 39 1941
Google Scholar
[27] Janszky J, Yushin Y 1989 Phys. Rev. A 39 5445
Google Scholar
[28] Aliga J, Crespo G, Proto A N 1990 Phys. Rev. A 42 618
Google Scholar
[29] Lo C F 1990 Phys. Scr. 42 389
Google Scholar
[30] Lo C F 1990 J. Phys. A 23 1155
Google Scholar
[31] Agarwal G S, Kumar S A 1991 Phys. Rev. Lett. 67 3665
Google Scholar
[32] Fan H Y, Zaidi H R 1989 Can. J. Phys. 67 152
Google Scholar
[33] Gerry C C, Plumb M F 1990 J. Phys. A 23 3997
Google Scholar
[34] Dodonov V V, Klimov A B, Man’ko V I 1990 Phys. Lett. A 149 225
Google Scholar
[35] Janszky J, Adam P 1992 Phys. Rev. A 46 6091
Google Scholar
[36] Xin M, Leong W S, Chen Z, Wang Y, Lan S Y 2021 Phys. Rev. Lett. 127 183602
Google Scholar
[37] Sompet P, Fung Y H, Schwartz E, Hunter M D J, Phrompao J, Andersen M F 2017 Phys. Rev. A 95 031403(R
Google Scholar
-
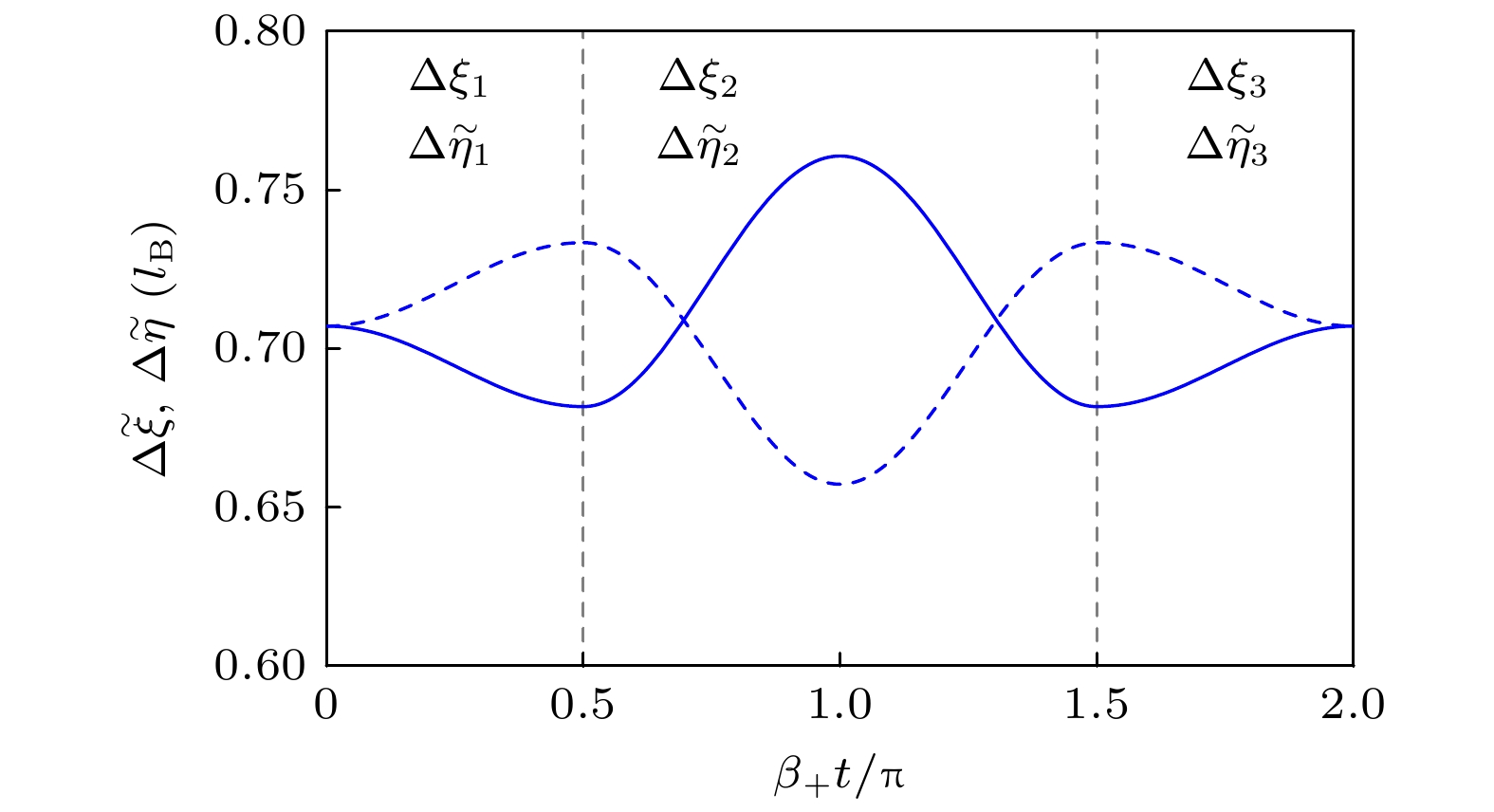
图 1 三次跳频下回旋半径涨落随$ \beta_+t $的演化过程, 其中$ \varepsilon = 0.125 $和$ \varOmega/\omega = 0.9 $. 实线和虚线分别表示$ \Delta \widetilde \xi $和$ \Delta \widetilde \eta $演化曲线
Fig. 1. Variances of cyclotron coordinates evolve with $ \beta_+t $ under three frequency jumping, where $ \varepsilon = 0.125 $ and $ \varOmega/\omega = 0.9 $. The solid and dashed lines respectively represent the evolution curves of $ \Delta \widetilde \xi $ and $ \Delta \widetilde \eta $.
图 2 变量$ (\varepsilon, \varOmega/\omega) $中, 两个压缩模式的相图
Fig. 2. In the variables$ (\varepsilon, \varOmega/\omega) $, the phase diagram of squeezing modes.
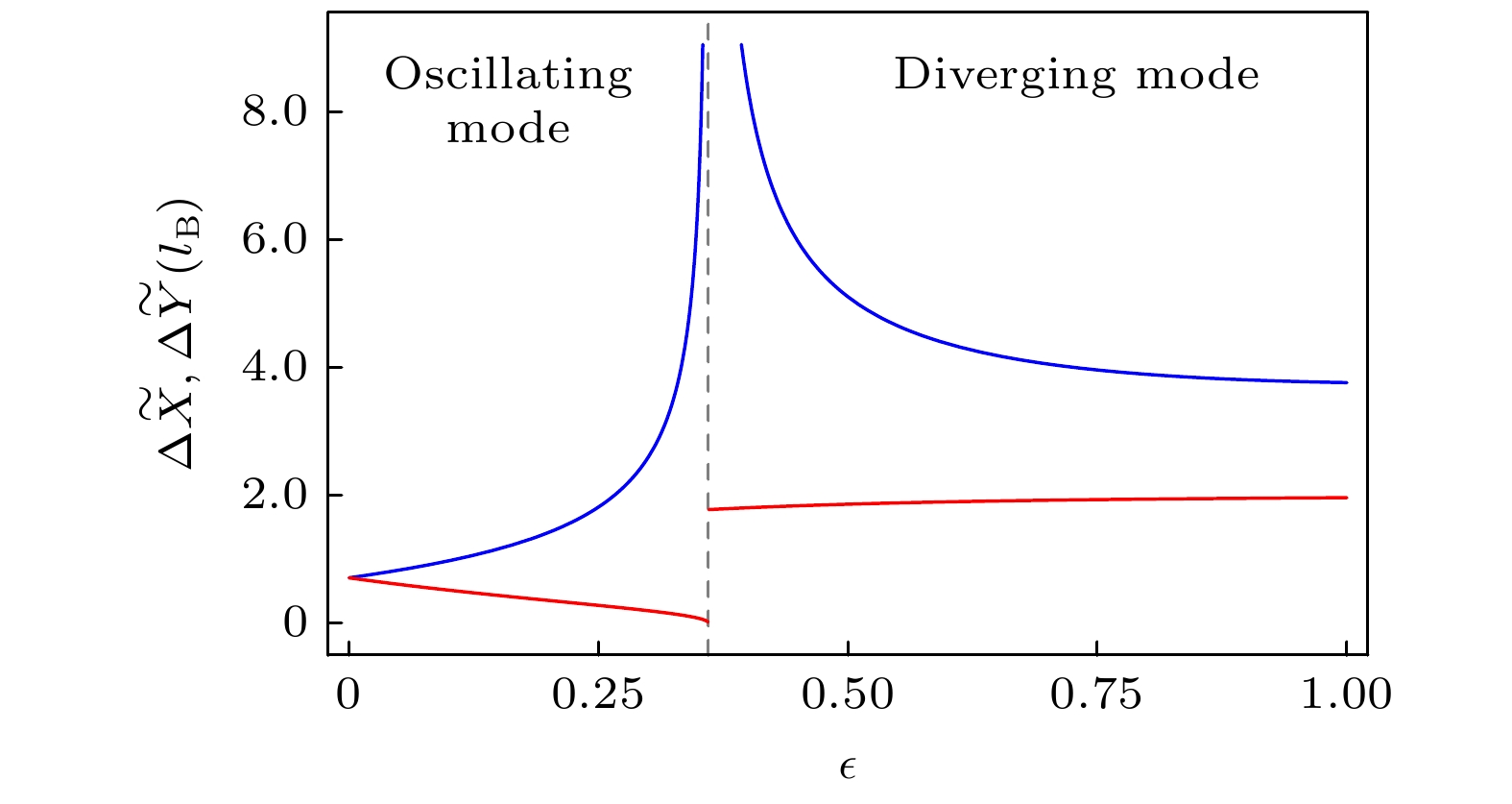
图 3 中心导向坐标$ \{\widetilde X, \widetilde Y\} $最大压缩量随$ \varepsilon $的变化曲线, 其中$ \varOmega/\omega = 0.8 $. 蓝线和红线分别为$ \Delta \widetilde X $和$ \Delta \widetilde Y $的曲线
Fig. 3. Variances of maximum squeezing of guiding center coordinates change with $ \varepsilon $, where $ \varOmega/\omega = 0.8 $. Blue and red lines represent $ \Delta \widetilde X $ and $ \Delta \widetilde Y $.
图 4 中心导向坐标$ \widetilde X $和$ \widetilde Y $在最大压缩量处的涨落 (a)振荡模式; (b)发散模式
Fig. 4. Fluctuations of guiding center coordinates $ \widetilde X $ and $ \widetilde Y $ at maximum squeezing: (a) Oscillation mode; (b) divergence mode.
-
[1] Burd S C, Srinivas R, Bollinger J J, Wilson A C, Wineland D J, Leibfried D, Slichter D H, Allcock D T C 2019 Science 364 1163
Google Scholar
[2] Fletcher R J, A Shaffer, Wilson C C, Patel P B, Yan Z, Crépel V, Mukherjee B, Zwierlein M W 2021 Science 372 1318
Google Scholar
[3] Sharma V, Mueller E J 2022 Phys. Rev. A 105 023310
Google Scholar
[4] Hu J, Chen W, Vendeiro Z, Urvoy A, Braverman B, Vuletić V 2017 Phys. Rev. A 96 050301
Google Scholar
[5] Shankar A, Tang Chen, Affolter M, Gilmore K, Dubin D H E, Parker S, Holland M J, Bollinger J J 2020 Phys. Rev. A 102 053106
Google Scholar
[6] Maslowski T, Sedlmayr N 2023 Phys. Rev. B 108 094306
Google Scholar
[7] Yuen H P 1976 Phys. Rev. A 13 2226
Google Scholar
[8] Slusher R E, Hollberg L W, Yurke B, Mertz J C, Valley J F 1985 Phys. Rev. Lett. 55 2409
Google Scholar
[9] Hosten O, Engelsen N J, Krishnakumar R, Kasevich M A 2016 Nature 529 505
Google Scholar
[10] Wollman E E, Lei C U, Weinstein A J, Suh J, Kronwald A, Marquardt F, Clerk A A, Schwab K C 2015 Science 349 952
Google Scholar
[11] Lecocq F, Clark J B, Simmonds R W, Aumentado J, Teufel J D 2015 Phys. Rev. X 5 041037
Google Scholar
[12] Pirkkalainen J M, Damskägg E, Brandt M, Massel F, Sillanpää M A 2015 Phys. Rev. Lett. 115 243601
Google Scholar
[13] Meekhof D M, Monroe C, E King B, M Itano W, Wineland D J 1996 Phys. Rev. Lett. 76 1796
Google Scholar
[14] Kienzler D, Lo H Y, Keitch B, de Clercq L, Leupold F, Lindenfelser F, Marinelli M, Negnevitsky V, Home J P 2015 Science 347 53
Google Scholar
[15] Meylahn F, Willke B, Vahlbruch H 2022 Phys. Rev. Lett. 129 121103
Google Scholar
[16] Pezzè L, Smerzi A 2020 Phys. Rev. Lett. 125 210503
Google Scholar
[17] Li T, Wang W, Yi X 2021 Phys. Rev. A 104 013521
Google Scholar
[18] Yurke B, McCall S L, Klauder J R 1986 Phys. Rev. A 33 4033
Google Scholar
[19] Davis E, Bentsen G, Schleier-Smith M 2016 Phys. Rev. Lett. 116 053601
Google Scholar
[20] Linnemann D, Strobel H, Muessel W, Schulz J, Lewis-Swan R J, Kheruntsyan K V, Oberthaler M K 2016 Phys. Rev. Lett. 117 013001
Google Scholar
[21] Malnou M, Palken D A, Brubaker B M, Vale Leila R, Hilton Gene C, Lehnert K W 2019 Phys. Rev. X 9 021023
Google Scholar
[22] Eddins A, Schreppler S, Toyli D M, Martin L S, Hacohen-Gourgy S, Govia L C G, Ribeiro H, Clerk A A, Siddiqi I 2018 Phys. Rev. Lett. 120 040505
Google Scholar
[23] Janszky J, Yushin Y Y 1986 Opt. Commun. 59 151
Google Scholar
[24] Schleich W, Wheeler J A 1987 Nature 326 574
Google Scholar
[25] Graham R 1987 J. Mod. Opt. 34 873
Google Scholar
[26] Ma X, Rhodes W 1989 Phys. Rev. A 39 1941
Google Scholar
[27] Janszky J, Yushin Y 1989 Phys. Rev. A 39 5445
Google Scholar
[28] Aliga J, Crespo G, Proto A N 1990 Phys. Rev. A 42 618
Google Scholar
[29] Lo C F 1990 Phys. Scr. 42 389
Google Scholar
[30] Lo C F 1990 J. Phys. A 23 1155
Google Scholar
[31] Agarwal G S, Kumar S A 1991 Phys. Rev. Lett. 67 3665
Google Scholar
[32] Fan H Y, Zaidi H R 1989 Can. J. Phys. 67 152
Google Scholar
[33] Gerry C C, Plumb M F 1990 J. Phys. A 23 3997
Google Scholar
[34] Dodonov V V, Klimov A B, Man’ko V I 1990 Phys. Lett. A 149 225
Google Scholar
[35] Janszky J, Adam P 1992 Phys. Rev. A 46 6091
Google Scholar
[36] Xin M, Leong W S, Chen Z, Wang Y, Lan S Y 2021 Phys. Rev. Lett. 127 183602
Google Scholar
[37] Sompet P, Fung Y H, Schwartz E, Hunter M D J, Phrompao J, Andersen M F 2017 Phys. Rev. A 95 031403(R
Google Scholar
下载:
计量
- 文章访问数: 1771
- PDF下载量: 82
- 被引次数: 0
