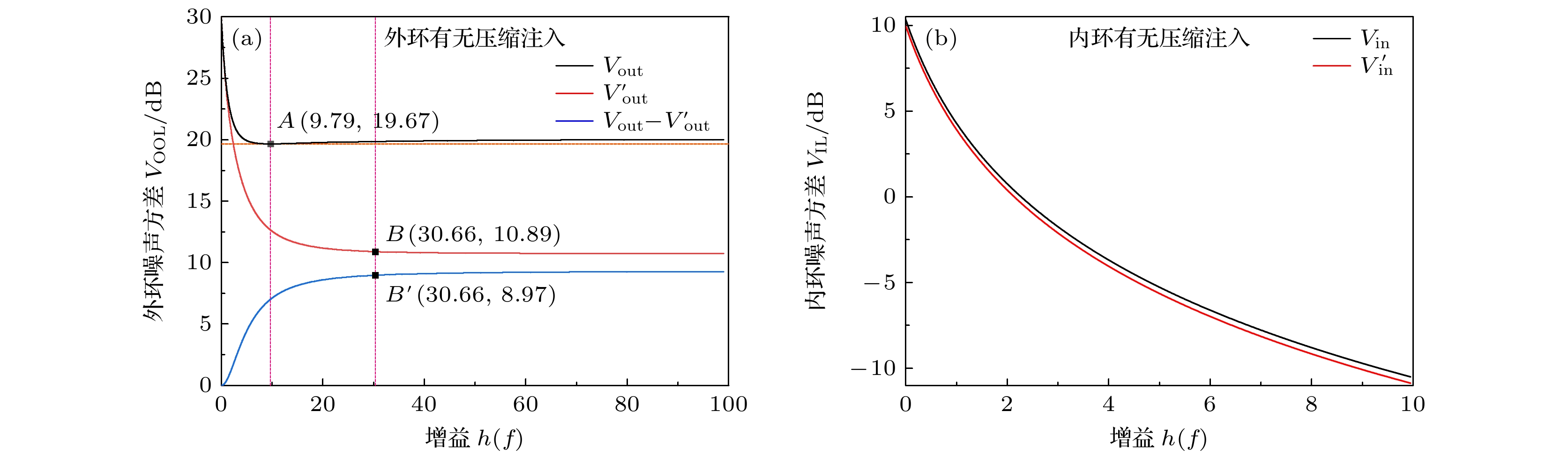
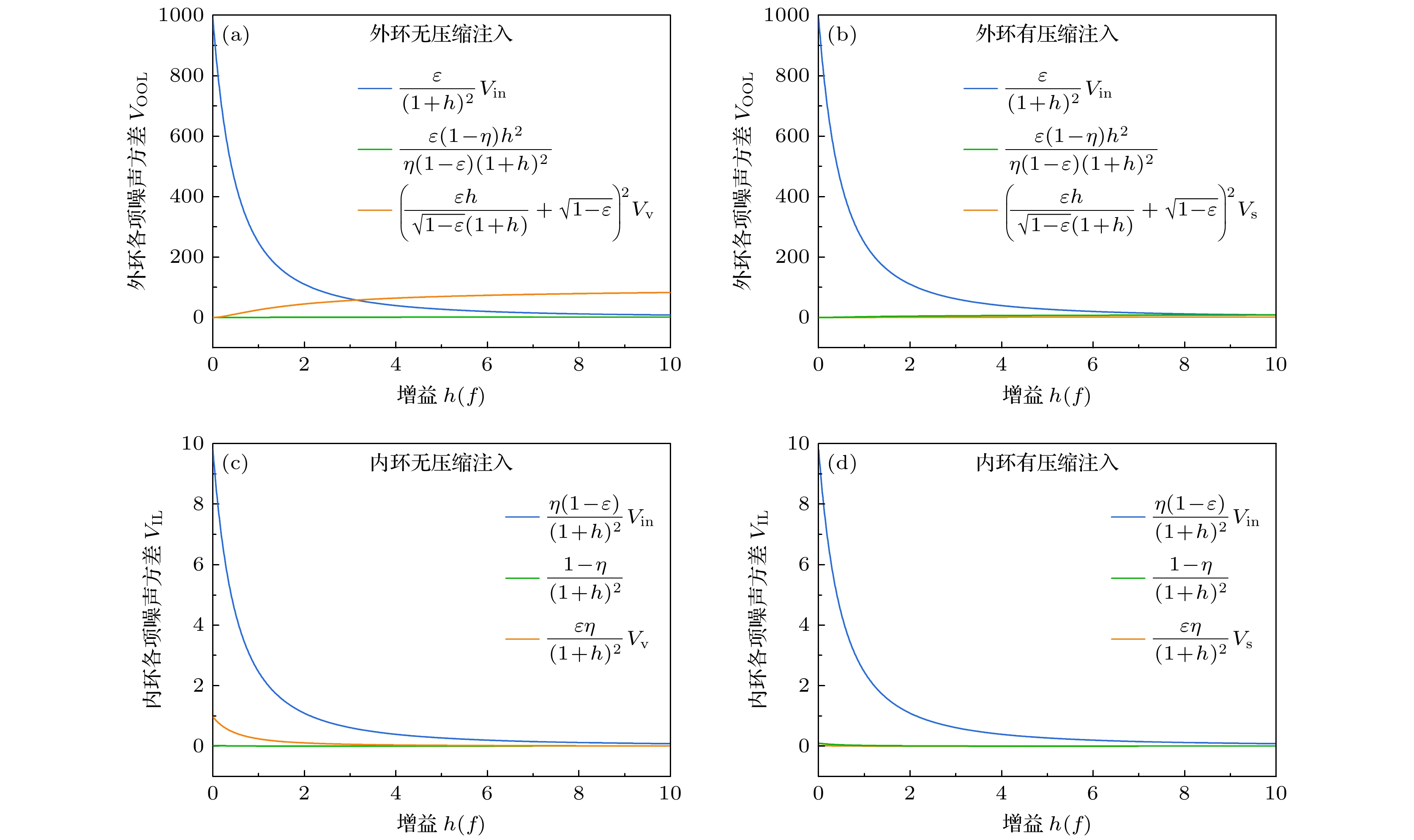
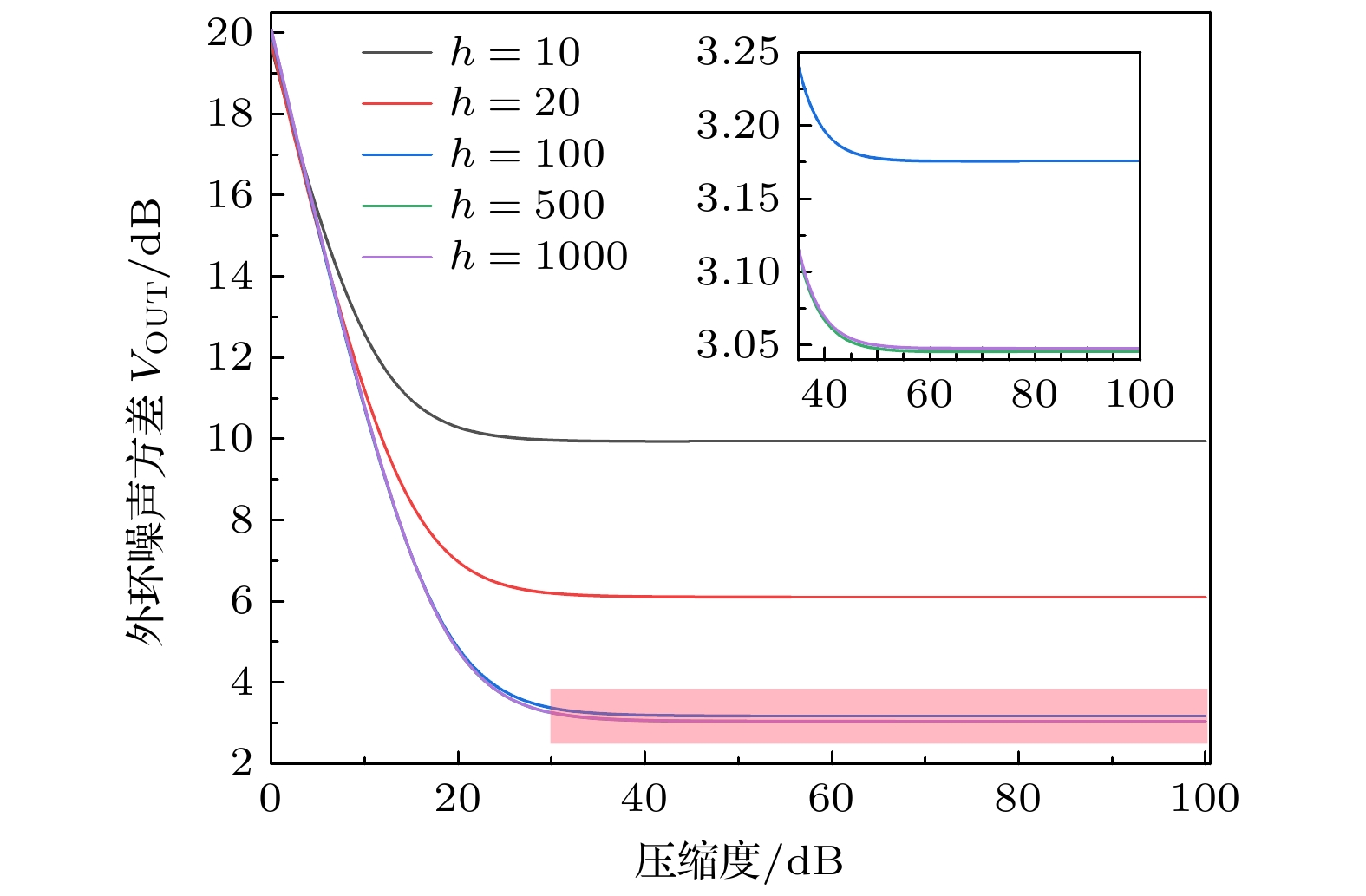
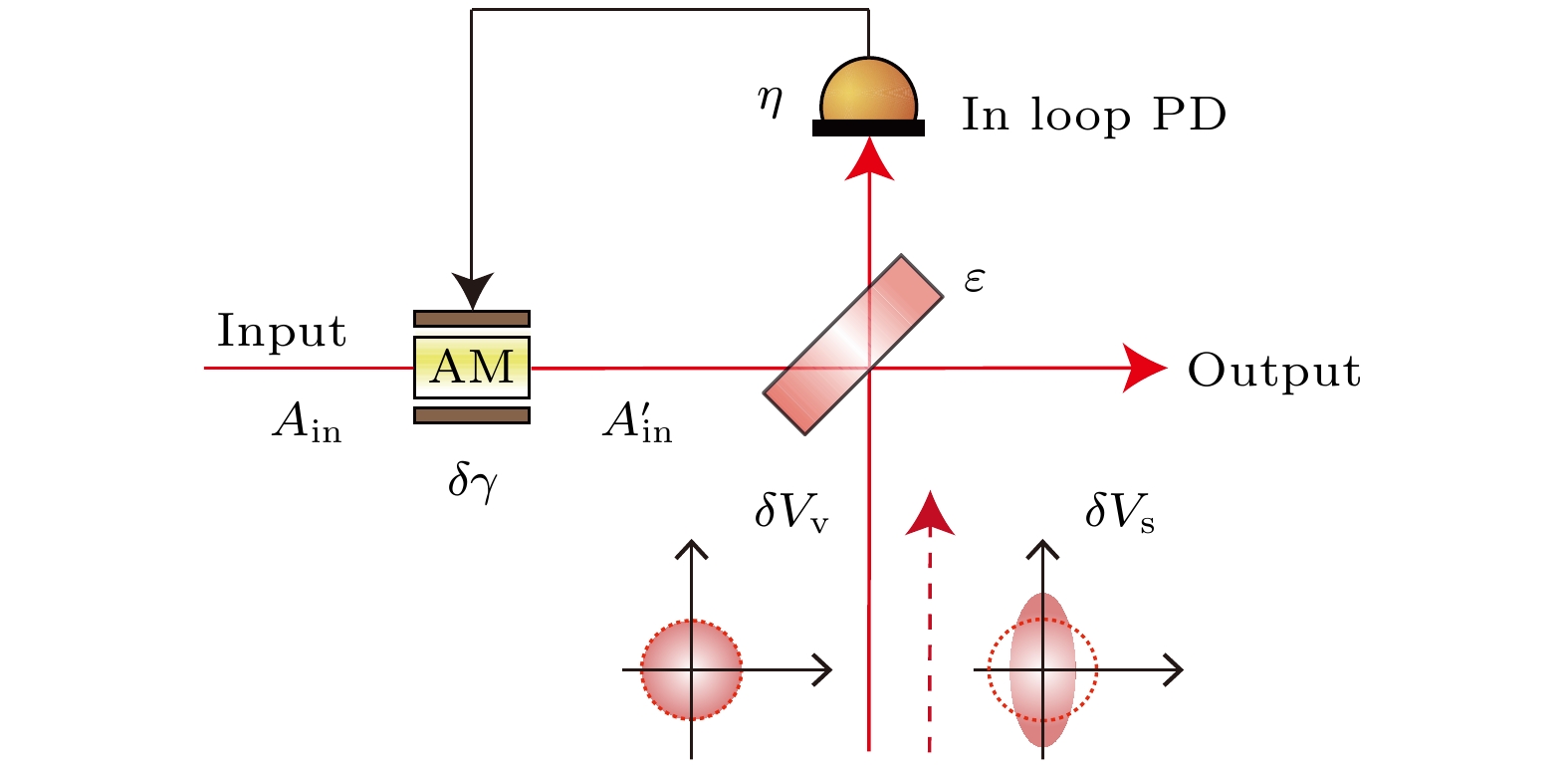
-
激光光源的噪声直接影响精密测量系统的精度和灵敏度，特别是在引力波探测和生物成像等高精度应用中。尽管经典反馈控制技术能有效抑制强度噪声，但其降噪水平受到经典噪声极限的限制。本研究提出一种结合量子压缩光与经典反馈控制技术的新方法，旨在进一步降低系统中的强度噪声，突破经典反馈控制技术的抑噪瓶颈。通过引入正交振幅压缩态光场，在理论上建立了压缩光辅助的反馈控制系统，理论分析了反馈增益和压缩度对噪声抑制的影响，并与经典方案进行对比。理论分析结果表明，压缩光的引入显著提高了噪声抑制水平，接近散粒噪声极限，从而大幅提升系统的灵敏度。该方法为在不增加激光功率的情况下实现更低噪声水平提供了新的量子控制手段，对精密测量技术的发展具有重要意义。This research focuses on advanced noise suppression techniques for high-precision measurement systems, particularly addressing the limitations of classical noise reduction approaches. The noise level of laser sources is a crucial factor that directly impacts measurement sensitivity in applications such as gravitational wave detection and biomedical imaging. Classical feedback control techniques have been effective but often hit a bottleneck defined by the classical noise suppression limits. To overcome these challenges, this study proposes a novel method integrating quantum squeezed light with classical feedback control systems to achieve enhanced intensity noise reduction. By employing an amplitude-squeezed light field, a quantum-enhanced feedback control model is developed, theoretically examining the impact of both the feedback loop gain and the degree of squeezing on the noise suppression performance. The results show that the injection of squeezed light significantly reduces the intensity noise, approaching the shot noise limit (SNL), thereby improving the system's sensitivity beyond the classical noise reduction boundaries. Specifically, -10 dB squeezed state injection into the feedback system yielded an additional noise suppression of approximately 8.97 dB, surpassing what is achievable using classical feedback alone. This demonstrates the potential of the proposed approach for pushing measurement precision closer to the quantum noise limits without increasing the laser power.The analysis highlights the asymmetric noise suppression effects between the inner and outer feedback loops. While the outer loop benefits significantly from the squeezed light injection, achieving noise levels unattainable by classical feedback methods, the inner loop shows comparatively minor improvements. This asymmetry is attributed to the inherent characteristics of quantum squeezing and the limitations of the feedback loop design. Further investigation into the individual noise components reveals that the primary contributors to the intensity noise include input noise, photodetector noise, and beam splitter-induced vacuum fluctuations. The injection of squeezed light effectively mitigates these vacuum fluctuations, typically a major noise source in high-precision laser systems. Theoretical research results show that the use of squeezed light in feedback control systems can effectively enhance noise suppression equivalent to a tenfold increase in detected optical power, without the physical drawbacks of increasing laser power such as thermal noise. In conclusion, this study provides a theoretical validation of combining quantum squeezed states with classical feedback control to exceed classical noise suppression limits. The integration of a -10 dB squeezed state demonstrated significant noise reduction, showing that this hybrid approach could revolutionize noise management in precision measurement applications. The results pave the way for further exploration of quantum-enhanced control techniques in fields such as gravitational wave detection, quantum communication, and advanced optical sensing, offering a pathway to improved sensitivity and noise suppression without additional power requirements.
-
Keywords:
- Precision measurement /
- Squeezed state /
- Noise suppression /
- Feedback control
-
[1] The LIGO Scientific Collaboration 2015 Class. Quantum Grav. 32 074001
[2] AcerneseF, Agathos M, Agatsuma K, Aisa D, Allemandou N, Allocca A, Meidam J 2014 Class. Quantum Grav. 32 024001
[3] LIGO Scientific and Virgo Collaborations 2016 Phys. Rev. Lett. 116 061102
[4] LIGO Scientific and Virgo Collaborations) 2017 Phys. Rev. Lett. 119 141101
[5] Taylor M A, Janousek J, Daria V, Knittel J, Hage B, Bachor H A, Bowen W P 2013 Nat. Photonics 7 229
[6] Casacio C A, Madsen L S, Terrasson A, Waleed M, Barnscheidt K, Hage B, Bowen W P 2021 Nature. 594 201
[7] Brito R, Ghosh S, Barausse E, Berti E, Cardoso V, Dvorkin I, Klein A, Pani P 2017 Phys. Rev. D 96 064050
[8] Armano M, Audley H, Baird J, Binetruy P, Born M, Bortoluzzi D, Zweifel P 2018 Phys. Rev. Lett. 120 061101
[9] Kaufer S, Kasprzack M, Frolov V, Willke B 2017 Class. Quantum Grav. 34 145001
[10] Seifert F, Kwee P, Heurs M, Willke B, Danzmann K 2006 Opt. Lett. 31 2000
[11] Kwee P, Willke B, Danzmann K 2009 Opt. Lett. 34 2912
[12] Junker J, Oppermann P, Willke B 2017 Opt. Lett. 42 755
[13] Wang J P, Zhang W H, Li R X, Tian L, Wang Y J, Zheng Y H 2020 Acta Phys. Sin. 69 234204 (in Chinese) [王俊萍，张文慧，李瑞鑫，田龙,，王雅君，郑耀辉2020 69 234204]
[14] Wang Y J, Wang J P, Zhang W H, Li R X, Tian L, Zheng Y H 2021 Acta Phys. Sin. 70 204202 (in Chinese) [王雅君，王俊萍，张文慧，李瑞鑫，田龙，郑耀辉2021 70 204202]
[15] Yamamoto Y, Haus H A 1986 Rev. Mod. Phys. 58 1001
[16] Xiao M, Wu L A, Kimble H J 1987 Phys. Rev. Lett. 59 27
[17] Zhao J, Guiraud G, Pierre C, Floissat F, Casanova A, Hreibi A, Chaibi W, Traynoer N, Boullet J, Santarelli G 2018 Appl. Phys. B 124 1
[18] Paschotta R, Fiedler K, Kurz P, Mlynek J 1995 Appl. Phys. B 60 241
[19] Haus H A, Yamamoto Y. 1984 Phys. Rev. A 29 1268
[20] Zhang J, Ma H L, Xie C D, Peng K C 2003. Appl. Opt. 42 1068
[21] Wang Z Y, Wang J H, Li Y H, Liu Q 2023 Acta Phys. Sin. 72 054205 (in Chinese) [王在渊，王洁浩，李宇航，柳强2023 72 054205]
[22] Wang Y J, Gao L, Zhang X L, Zheng Y H 2020 Infrared Laser Eng. 49 20201073 (in Chinese) [王雅君，高丽，张晓莉，郑耀辉 2020红外与激光工程 49 20201073]
[23] Kwee P, Willke B, Danzmann K 2008 Opt. Lett. 33 1509
[24] Kwee P, Willke B, Danzmann K 2011 Opt. Lett. 36 3563
[25] Kaufer S, Willke B 2019 Opt. Lett. 44 1916
[26] Yao D M, Guo G C 1988 Acta Phys. Sin. 37 463 (in Chinese) [姚德民，郭光灿 1988 37 463]
[27] Vahlbruch H, Wilken D, Mehmet M, Willke B 2018 Phys. Rev. Lett. 121 173601
[28] Eberle T, Steinlechner S, Bauchrowitz J, Händchen V, Vahlbruch H, Mehmet M, Müller-Ebhardt H, Schnabel R 2010 Phys. Rev. Lett. 104 251102
[29] Liu F, Zhou Y Y, Yu J, Guo J L, Yang W, Xiao S X, Dan W, Zhang Y, Jia X J, Xiao M 2017 Appl. Phys. Lett. 110
[30] Wu L A, Kimble H J, Hall J L, Wu H F 1986 Phys. Rev. Lett. 57 2520
[31] Schneider K, Lang M, Mlynek J, Schiller S 1998 Opt. Express 2 59
[32] Vahlbruch H, Chelkowski S, Danzmann K, Schnabel R 2007 New J. Phys. 9 371
[33] Vahlbruch H, Mehmet M, Danzmann K, Schnabel R 2016 Phys. Rev. Lett. 117 110801
[34] Kleybolte L, Gewecke P, Sawadsky A, Korobko M, Schnabel R 2020 Phys. Rev. Lett. 125 213601
[35] Meylahn F, Willke B, Vahlbruch H 2022 Phys. Rev. Lett. 129 121103
[36] Yang W H, Jin X L, Yu X D, Zheng Y H, Peng K C 2017 Opt. Express 25 24262
[37] Zhang W H, Wang J R, Zheng Y H, Wang Y J, Peng K C 2019 Appl. Phys. Lett. 115 171105
[38] Pan J W 2024 Acta Phys. Sin 73 010301 (in Chinese) [潘建伟 2024 73 010301]
[39] Clerk A A, Devoret M H, Girvin S M, Marquardt F, Schoelkopf R. J 2010 Rev. Mod. Phys. 82 1155
[40] Aspelmeyer M, Kippenberg T J, Marquardt F 2014 Rev. Mod. Phys. 86 1391
计量
- 文章访问数: 51
- PDF下载量: 1
- 被引次数: 0
下载:
