-
In previous work [Acta Phys. Sin. 60 054501 (2011)], we found that for inclined Granular Orifice Flow (GOF) in air, regardless of the orifice size, the flow rate Q had a good linear relationship with the cosine of the inclination
$\cos \theta $ , i.e.$\dfrac{Q}{{{Q_0}}} = 1 - \dfrac{{\cos \theta - 1}}{{\cos {\theta _{\rm c}} - 1}}$ , where Q0 is flow rate at$\theta ={0^ \circ }$ , and${\theta _{\rm c}}$ is the critical angle of flow ceasing obtained by linear extrapolation. Moreover,${\theta _{\rm c}}$ increased linearly with ratio between grain and orifice diameter d/D, and at the limit of d/D going to zero (that is, D going to infinity), the angle of repose of the sample${\theta _{\rm r}}~( = 180^ \circ - \theta _{\rm c\infty})$ was obtained. Since the flow of GOF is very stable, we believe that the linear extrapolation of the above-mentioned inclined GOF provides a novel method for accurately measuring the angle of repose of granular materials. This method has been proved to be effective in a wider orifice size range by another work [Acta Phys. Sin. 65 084502 (2016)]; and three angles, namely the repose angle measured by GOF, the free accumulation angle of a sandpile and the internal friction angle of the granular material measured by Coulomb yielding, are confirmed to be consistent. In this work, we extend this method to underwater, measuring the mass flow rate of a granular sample (glass beads) which completely immersed in water and driven by gravity, discharged from an inclined orifice for various inclination angles and orifice diameters. It is found that similar to the case in air, regardless of the orifice size, the flow rate increase linearly with the cosine of the inclination; the critical angle of flow ceasing increases linearly with ratio between grain and orifice diameter; at the limit of infinite orifice, this critical angle is consistent with the repose angle of the underwater sample within the experimental error range. In addition, all measurements can be well fitted by using the Beverloo formula$Q = {C_0}\rho {g^{1/2}}{(D - kd)^{5/2}}$ , where the parameters C0 and k are only related to the cosine of the inclination, and are linear and inversely squared, respectively. Compared with the results of GOF in air reported by previous work, it is found that the difference mainly comes from the influence of buoyancy and fluid drag forces on the parameter C0. These results show that both the method of measuring angle of repose with the inclined GOF and the Beverloo formula have certain universality. The behavior of GOF is qualitatively the same whether the interstitial fluid is water or air.-
Keywords:
- granular matter /
- inclined orifice flow /
- angle of repose /
- Beverloo formula
[1] Nedderman R M1992 Statics and Kinematics of Granular Materials (Cambridge: Cambridge University Press) pp292–294
[2] 陆坤权, 刘寄星 2004 物理 33 713
Google Scholar
Lu K Q, Liu J X 2004 Physics 33 713
Google Scholar
[3] Beverloo W A, Lenginer H A, van de Velde J 1961 Chem. Eng. Sci. 15 260
Google Scholar
[4] Tian Y, Lin P, Zhang S, Wang C L, Wan J F, Yang L 2015 Adv. Powder Technol. 26 1191
Google Scholar
[5] Lin P, Zhang S, Qi J, Xing Y M, Yang L 2015 PhysicaA 417 29
Google Scholar
[6] Zhang S, Lin P, Yang G, Wan J F, Tian Y, Yang L 2019 Chin. Phys. B 28 018101
Google Scholar
[7] Rubio-Largo S M, Janda A, Maza D, Zuriguel I, Hidalgo R C 2015 Phys. Rev. Lett. 114 238002
Google Scholar
[8] Janda A, Zuriguel I, Maza D 2012 Phys. Rev. Lett. 108 248001
Google Scholar
[9] van Zuilichem D J, van Egmond N D, DeSwart J G 1974 Powder Technol. 10 161
Google Scholar
[10] Peng Z, Zheng H P, Jiang Y M 2009 arXiv: 0908.0258 v3 [cond-mat.soft]
[11] Madrid M A, Darias J R, Pugnaloni L A 2018 EPL 123 14004
Google Scholar
[12] Ji S Y, Wang S Q, Peng Z 2019 Powder Technol. 356 702
Google Scholar
[13] Sheldon H G, Durian D J 2010 Granul. Matter 12 579
Google Scholar
[14] Thomas C C, Durian D J 2015 Phys. Rev. Lett. 114 178001
[15] Thomas C C, Durian D J 2013 Phys. Rev. E 87 052201
Google Scholar
[16] 彭政, 蒋亦民 2011 60 054501
Google Scholar
Peng Z, Jiang Y M 2011 Acta Phys. Sin. 60 054501
Google Scholar
[17] 张昱, 韦艳芳, 彭政, 蒋亦民, 段文山, 厚美瑛 2016 65 084502
Google Scholar
Zhang Y, Wei YF, Peng Z, Jiang YM, Duan WS, Hou MY 2016 Acta Phys. Sin. 65 084502
Google Scholar
[18] Wilson T J, Pfeifer C R, Mesyngier N, Durian D J 2014 Pap. Phys. 6 060009
[19] Koivisto J, Durian D J 2017 Nature Comm. 8 15551
Google Scholar
[20] Hu W R, Zhao J F, Long M, Zhang X W, Liu Q S, Hou M Y, Kang Q, Wang Y R, Xu S H, Kong W J, Zhang H, Wang S F, Sun Y Q, Hang H Y, Huang Y P, Cai W M, Zhao Y, Dai J W, Zheng H Q, Duan E K, Wang J F 2014 Microgravity Sci. Technol. 26 159
Google Scholar
[21] Cheng X H, Xiao S Z, Cao A S, Hou M Y 2019 Granul. Matter 21 104
Google Scholar
[22] Kobayashi T, Ochiai H, Suyama Y, Aoki S, Yasufuku N, Omine K 2009 Soils Found. 49 115
Google Scholar
-
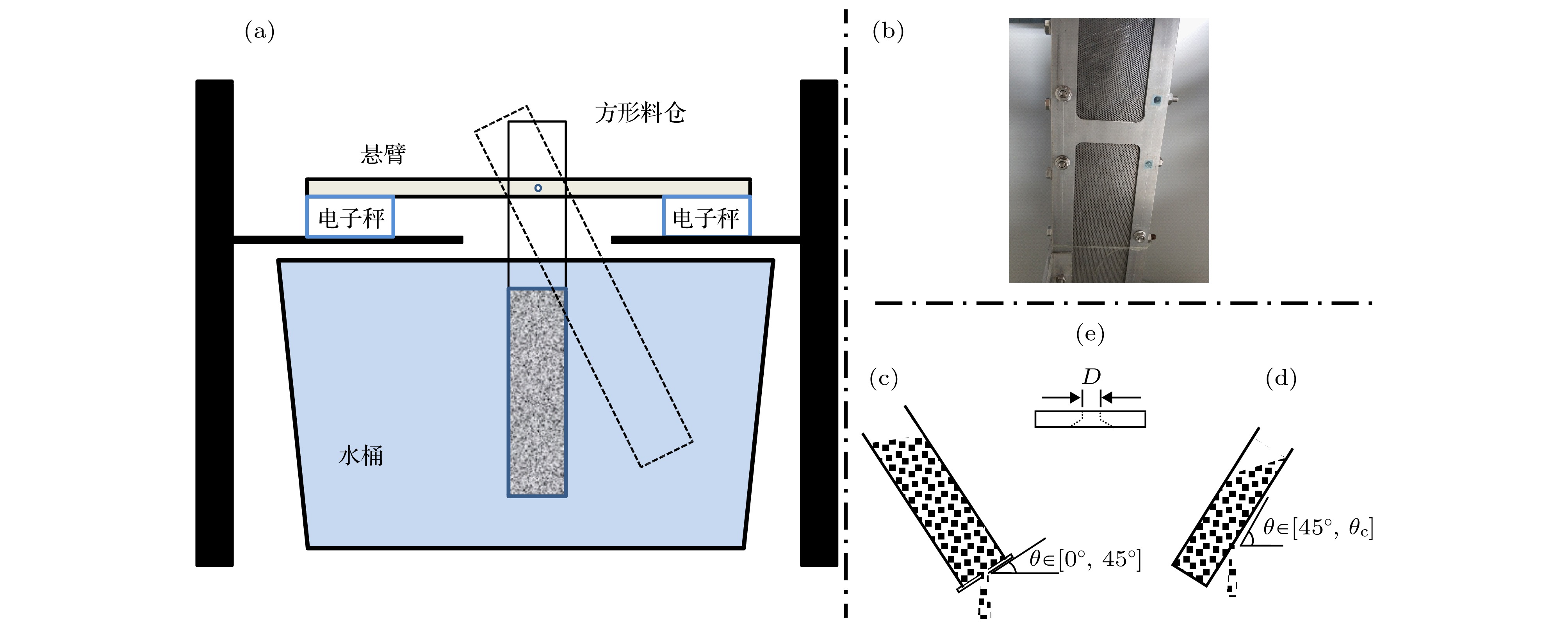
图 1 (a)实验装置示意图; (b)料仓透水侧壁照片; (c)倾角小于45度时采用的实验装置; (d)倾角大于45度时采用的实验装置; (e)楔形孔洞示意图
Figure 1. (a) Schematic of the setup; (b) photograph of the permeable side wall of the silo; (c) the experimental devices used when the inclination is less than 45 degrees; (d) the experimental devices used when the inclination is greater than 45 degrees; (e) schematic of the wedge-shaped orifice D.
图 2
$D = 14$ mm,$\theta = 90^\circ $ 时典型的$M(t)$ 数据; 左下和右上插图分别为从主图中摘出的40−80 s及80−120 s的$M(t)$ 数据, 均呈良好的线性关系. 由这两段数据计算得到的流量$Q$ 没有差别, 均为6.53 g/s, 表明流量非常稳定Figure 2. Typical data of M(t) at D = 14 mm,
$\theta = 90^\circ $ ;the lower left and upper right insets are the data of 40−80 s and 80−120 s extracted from the main graph, both of which show good linearity. Both flow rates$Q$ calculated from these two insets are 6.53 g/s, indicating that the flow is very stable.
图 3 (a)不同孔径D下流量Q随倾角余弦
$\cos \theta $ 的变化, 实线为直线拟合; (b)用水平($\theta = {0^\circ }$ )流量${Q_0}$ 归一化的流量$Q/{Q_0}$ 随倾角余弦$\cos \theta $ 的变化关系, 实线为公式(3)的拟合结果; (c)临界流量休止角${\theta _{\rm{c}}}$ 随粒径-孔径比d/D的变化关系, 实线和${\theta _0}$ 为直线拟合结果Figure 3. (a) The variation of flow rateQ with the inclination cosine
$\cos \theta $ at different orifices D, where the solid line is a linear fit; (b) variation of the normalized flow rate$Q/{Q_0}$ with$\cos \theta $ , where${Q_0}$ is the rate at$\theta = {0^ \circ }$ , and the solid line is the fitted result of equation (3); (c) the relationship between the critical angle of flow ceasing${\theta _{\rm{c}}}$ and the ratio d/D, where the solid line and${\theta _0}$ are results of linear fitting.
图 4 (a)用Beverloo公式(1)和(2)拟合图3数据的结果, 插图为不同倾角时
${Q^{2/5}}$ 随D的变化关系, 实线为线性拟合; (b), (c)Beverloo参数${C_0}$ 和$k$ 随$\cos \theta $ 的变化关系, 及其用公式(2)的拟合情况. 图(c)中的插图是${k^{ - 2}}$ 随$\cos \theta $ 的变化关系Figure 4. (a) Results of fitting the data in Figure 3 using the Beverloo formula (1) and (2), the inset is the change of
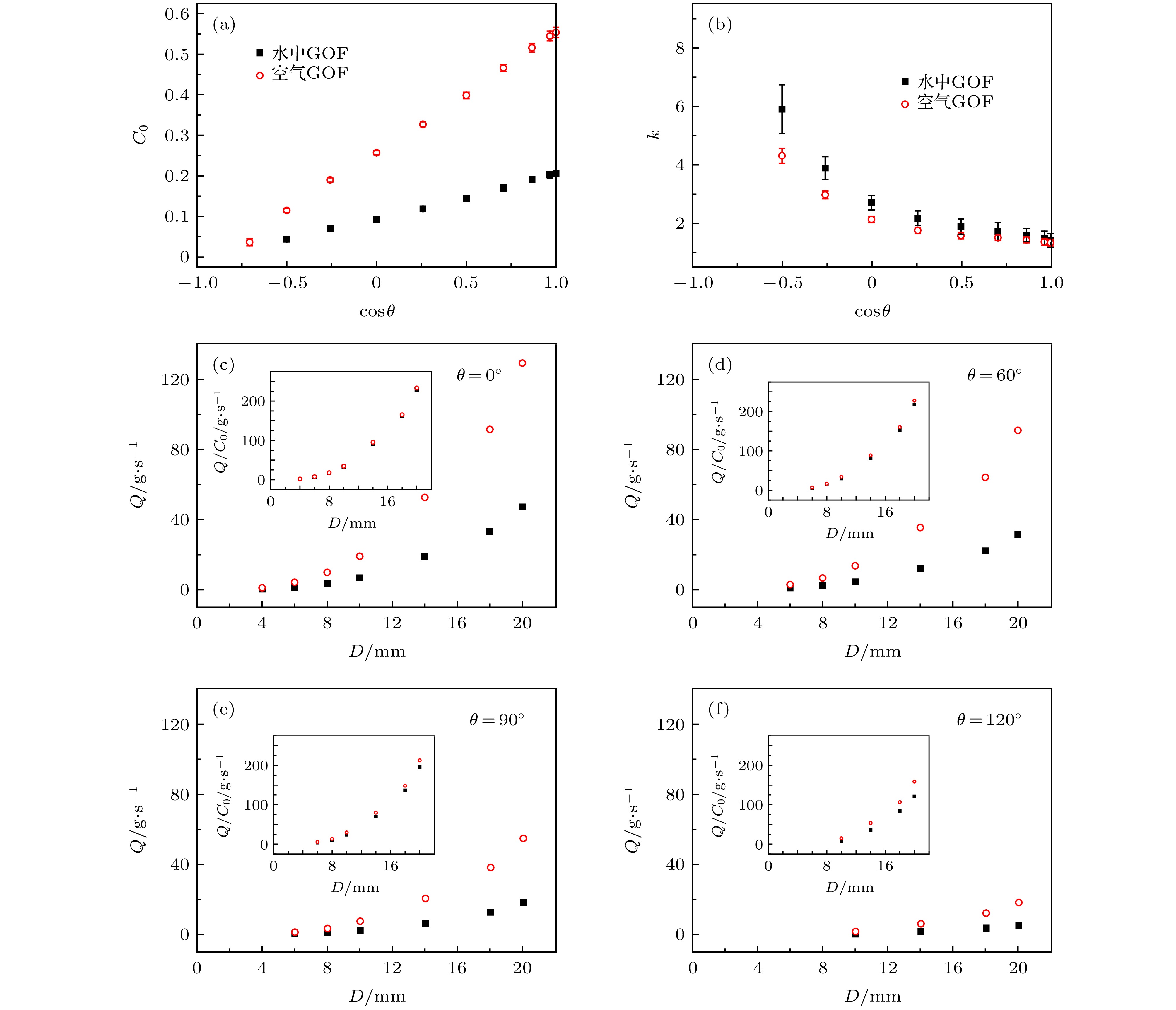
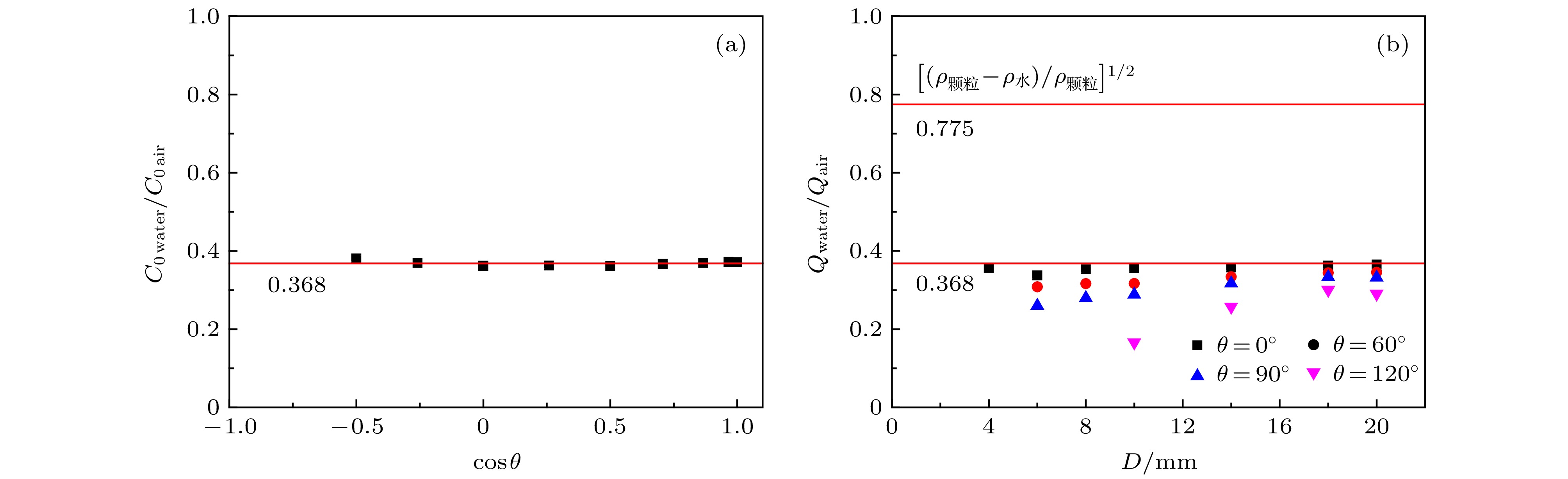
${Q^{2/5}}$ with D at different inclination, and the solid line is a linear fit; (b) and (c) variations of the parameters${C_0}$ and$k$ with$\cos \theta $ , and solid lines are results of fits by using equation (2). The inset in (c) is the change of${k^{ - 2}}$ with$\cos \theta $ .
图 5 (a)和(b)是水中(实心方点)和空气中(空心圆点)GOF的Beverloo参数
${C_0}$ 和k随$\cos \theta $ 的变化; (c)−(f)分别为$\theta = {0^ \circ }, {60^ \circ }, {90^ \circ }, {120^ \circ }$ 时, 水中和空气中GOF流量Q随D的变化, 插图是$Q/{C_0}$ 随D的变化. 空气中的实验数据来自文献[16]Figure 5. (a) and (b): Beverloo parameters
${C_0}$ and$k$ of GOF in water (solid squares) and in air (hollow circles) as a function of$\cos \theta $ ; (c)−(f): the changes of GOF flow rate Q with D in water and in air when$\theta = {0^ \circ }, {60^ \circ }, {90^ \circ }, {120^ \circ }$ , respectively, and the inset is the change of$Q/{C_0}$ with D. The experimental data in air comes from ref. [16].
-
[1] Nedderman R M1992 Statics and Kinematics of Granular Materials (Cambridge: Cambridge University Press) pp292–294
[2] 陆坤权, 刘寄星 2004 物理 33 713
Google Scholar
Lu K Q, Liu J X 2004 Physics 33 713
Google Scholar
[3] Beverloo W A, Lenginer H A, van de Velde J 1961 Chem. Eng. Sci. 15 260
Google Scholar
[4] Tian Y, Lin P, Zhang S, Wang C L, Wan J F, Yang L 2015 Adv. Powder Technol. 26 1191
Google Scholar
[5] Lin P, Zhang S, Qi J, Xing Y M, Yang L 2015 PhysicaA 417 29
Google Scholar
[6] Zhang S, Lin P, Yang G, Wan J F, Tian Y, Yang L 2019 Chin. Phys. B 28 018101
Google Scholar
[7] Rubio-Largo S M, Janda A, Maza D, Zuriguel I, Hidalgo R C 2015 Phys. Rev. Lett. 114 238002
Google Scholar
[8] Janda A, Zuriguel I, Maza D 2012 Phys. Rev. Lett. 108 248001
Google Scholar
[9] van Zuilichem D J, van Egmond N D, DeSwart J G 1974 Powder Technol. 10 161
Google Scholar
[10] Peng Z, Zheng H P, Jiang Y M 2009 arXiv: 0908.0258 v3 [cond-mat.soft]
[11] Madrid M A, Darias J R, Pugnaloni L A 2018 EPL 123 14004
Google Scholar
[12] Ji S Y, Wang S Q, Peng Z 2019 Powder Technol. 356 702
Google Scholar
[13] Sheldon H G, Durian D J 2010 Granul. Matter 12 579
Google Scholar
[14] Thomas C C, Durian D J 2015 Phys. Rev. Lett. 114 178001
[15] Thomas C C, Durian D J 2013 Phys. Rev. E 87 052201
Google Scholar
[16] 彭政, 蒋亦民 2011 60 054501
Google Scholar
Peng Z, Jiang Y M 2011 Acta Phys. Sin. 60 054501
Google Scholar
[17] 张昱, 韦艳芳, 彭政, 蒋亦民, 段文山, 厚美瑛 2016 65 084502
Google Scholar
Zhang Y, Wei YF, Peng Z, Jiang YM, Duan WS, Hou MY 2016 Acta Phys. Sin. 65 084502
Google Scholar
[18] Wilson T J, Pfeifer C R, Mesyngier N, Durian D J 2014 Pap. Phys. 6 060009
[19] Koivisto J, Durian D J 2017 Nature Comm. 8 15551
Google Scholar
[20] Hu W R, Zhao J F, Long M, Zhang X W, Liu Q S, Hou M Y, Kang Q, Wang Y R, Xu S H, Kong W J, Zhang H, Wang S F, Sun Y Q, Hang H Y, Huang Y P, Cai W M, Zhao Y, Dai J W, Zheng H Q, Duan E K, Wang J F 2014 Microgravity Sci. Technol. 26 159
Google Scholar
[21] Cheng X H, Xiao S Z, Cao A S, Hou M Y 2019 Granul. Matter 21 104
Google Scholar
[22] Kobayashi T, Ochiai H, Suyama Y, Aoki S, Yasufuku N, Omine K 2009 Soils Found. 49 115
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 7800
- PDF Downloads: 122
- Cited By: 0
