-
In this paper, the X-ray diffraction experiment with multiple crystals configuration and its application in characterizing the emission characteristics of double crystal monochromator (DCM) on BL09 beamline of Shanghai Synchrotron Radiation Facility (SSRF) are reported. It is a non-dispersion configuration when the second crystal of DCM and the crystal analyzer form a (+n, –n) type experimental configuration. The rocking curve of the analyzer crystal can only reflect the operation of the DCM. It is the dispersion configurations when the second crystal of DCM and the crystal analyzer form the (+n, +n), (+n, –m) and (+n, +m) type experimental configuration. The width of the analyzer crystal rocking curve includes not only the intrinsic bandwidth of the DCM and the analyzer crystal, but also the angular divergence of the beamline. In this paper, we use the method of DuMond diagram to explicitly illustrate the characteristics of the output beam of the DCM which can be measured under the above two kinds of experimental configurations, and distinguish the diffraction characteristics of different experimental configurations at the same time. Finally, the angular bandwidth and the relative energy bandwidth of the DCM are 5.40(4) arcsec and1.30(1) × 10–4 @ 10 keV, respectively, which are obtained by deconvolution of the analyzer crystal in (+1, –1) nondispersive configuration. The angular distribution and the relative energy bandwidth of the synchrotron radiation beams are 26(1) arcsec and 6.3(2) × 10–4 @ 10 keV, respectively, which are obtained by deconvolution of the analyzer crystal and removal of dispersion broadening in (+1, +1), (+1, –3) and (+1, +3) dispersion configuration. After removing the influence of the DCM, the obtained angular divergence of the light source by 25(1) arcsec @ 10 keV, is consistent with the theoretical value of the bending source. In addition, under a series of different white beam entrance slit widths, we characterize the divergence and bandwidth of the beam emitted from the monochromator by the method of multi-crystals dispersion configuration and the DuMond diagram.
-
Keywords:
- synchrotron radiation /
- double crystal monochromator /
- multiple crystals X-ray diffraction /
- energy bandwidth /
- DuMond diagram
[1] Jiang X M, Zheng W L, Wu J, Jing Y, Liu G 1995 Rev. Sci. Instrum. 66 1694
Google Scholar
[2] Zhang Z Y, Chen M, Tong Y J, Ji T, Zhu H C, Peng W W, Zhang M, Li Y J, Xiao T Q 2014 Infrared Phy. Tech. 67 521
Google Scholar
[3] Fischetti R F, Yoder D W, Xu S L, et al. 2007 9th International Conference on Synchrotron Radiation Instrumentation Daegu, Korea, May 28–June 2, 2006 p754
[4] Yu H S, Wei X J, Li J, et al. 2015 Nucl. Sci. Tech. 26 4
Google Scholar
[5] Liermann H P, Konopkova Z, Morgenroth W, et al. 2015 J. Synchrotron Rad. 22 908
Google Scholar
[6] Tian F, Li X H, Wang Y Z, et al. 2015 Nucl. Sci. Tech. 26 1
Google Scholar
[7] Yamaoka H, Hiraoka N, Ito M, et al. 2000 J. Synchrotron Rad. 7 69
Google Scholar
[8] Dippel A C, Liermann H P, Delitz J T, et al. 2015 J. Synchrotron Rad. 22 675
Google Scholar
[9] Seto M, Yoda Y, Kikuta S 1995 Phys. Rev. Lett. 74 3828
Google Scholar
[10] Zhang X, Mochizuki T, Sugiyama H 1992 Rev. Sci. Instrum. 63 404
Google Scholar
[11] Beaumont J H, Hart M 1974 J. Phys. E: Sci. Intum. 7 823
Google Scholar
[12] Zhang X, Hiroyuki F 2006 Jpn. J. Appl. Phys. 45 7933
Google Scholar
[13] Yang T Y, Wen W, Yin G Z, et al. 2015 Nucl. Sci. Tech. 26 20101
Google Scholar
[14] Wang S S, Kong R H, Shan X B, et al. 2006 J. Synchrotron Rad. 13 415
Google Scholar
[15] Puik E J, Dorssen G E, Eiel K J 1991 J. Vac. Sci. Technol. A: Vacuum, Surfaces, and Films 9 3142
Google Scholar
[16] Gong X, Lu Q 2015 J. X-ray Sci. Technol 23 409
Google Scholar
[17] DuMond J W M 1937 Phys. Rev. 52 872
Google Scholar
[18] Zhao Z T, Xu H J 2004 Proceedings of European Particle Accelerator Conference Lucerne, Switzerland, June 5–9, 2004 p2368
[19] Batterman B W, Cole H 1964 Rev. M. Phys. 36 682
Google Scholar
[20] Punegov V L, Pavlov K M, Karpov A V 2017 J. Appl. Cryst. 50 1256
Google Scholar
-
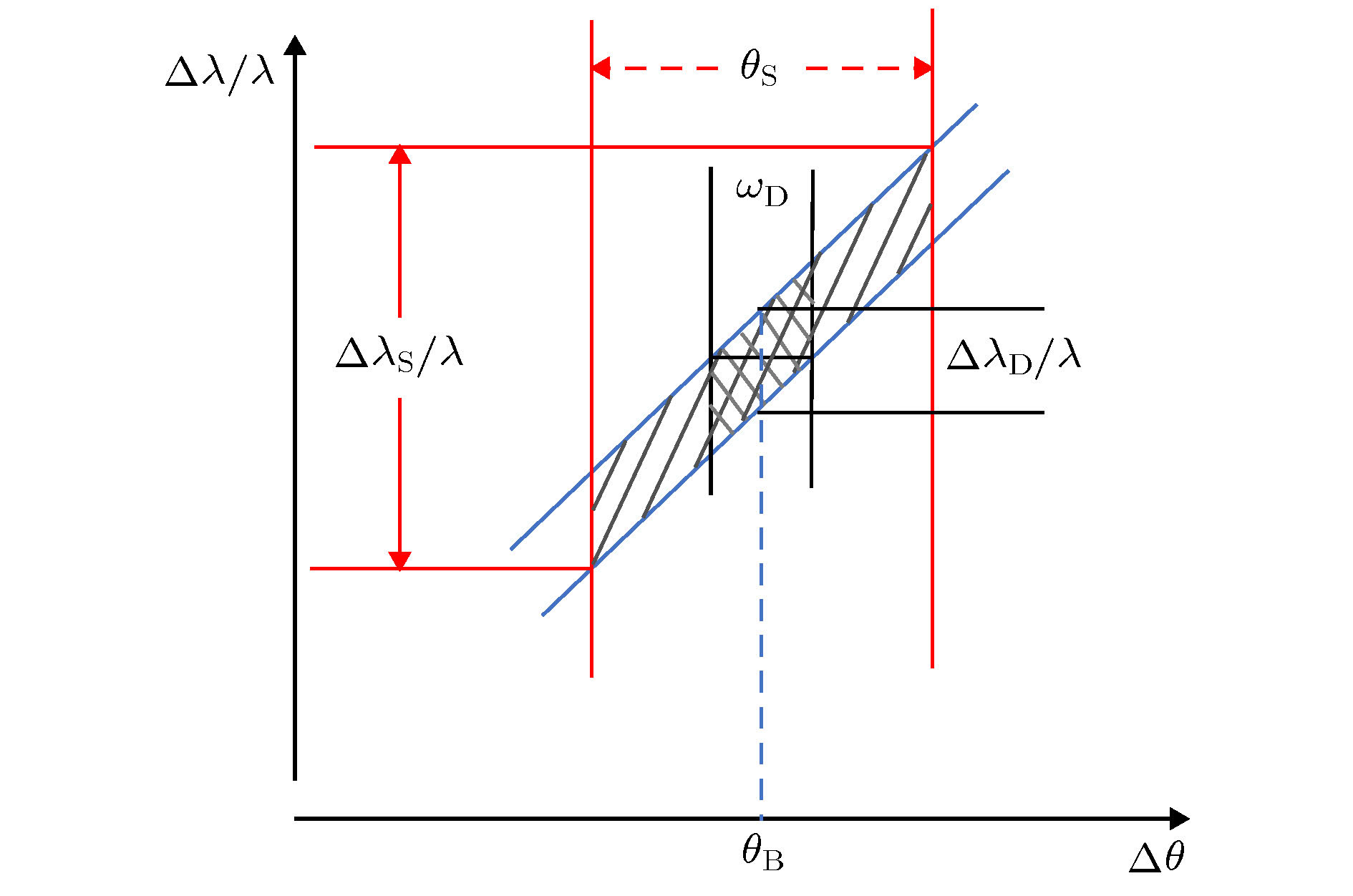
图 1 完美晶体对称反射的DuMond图. 微分衍射(2)式在图中对应的是一条斜率为
$ {\rm{cot}}{\theta }_{\rm{B}} $ 的直线带.$ {\theta }_{\rm{B}} $ 是运动学衍射角(晶体的折射率对X线衍射的角度位置有影响, 本文暂不考虑此方面的影响),$ {\omega }_{\rm{D}} $ 是动力学衍射的达尔文宽,$ {\theta }_{\rm{S}} $ 是光束的发散角. 当完全平行的白光入射时, 对称反射晶体的可接收和出射角度都是$ {\omega }_{\rm{D}} $ , 有限的角度宽带来了相应的波长分布${{\Delta \lambda}_{\rm{D}}}/{\lambda} $ . 当入射的白光带有一定的角发散时, 入射晶体的角分布变大, 影响带宽的角发散也由$ {\omega }_{\rm{D}} $ 变为$ {\theta }_{\rm{S}} $ , 角度发散带来的波长分布也变成了${{\Delta \lambda}_{\rm{S}}}/{\lambda} $ Figure 1. DuMond diagram for the symmetric Bragg geometry. The differential equation (2) of diffraction formula corresponds to the line band with a slope of
$ {\rm{cot}}{\theta }_{\rm{B}} $ .$ {\theta }_{\rm{B}} $ and$ {\omega }_{\rm{D}} $ represent the kinematic diffraction angle and the Darwin width of the dynamic diffraction, respectively. In this article, we ignore the change of X-ray diffraction angle position which is influenced by crystal refraction. When the incident white beam is completely parallel, both the receiving and emitting angle of the symmetric crystal are the same, which can be represented by$ {\omega }_{\rm{D}} $ . The limited angle broadband introduces the corresponding wavelength distribution${{\Delta \lambda}_{\rm{D}}}/{\lambda} $ . When the incident beam with a divergence angle, the distribution of the incident angle on the crystal becomes larger which affects the angular divergence of bandwidth changing from$ {\omega }_{\rm{D}} $ to$ {\theta }_{\rm{S}} $ (the divergence angle of the beam) and the wavelength distribution changing to$ {{\Delta \lambda}_{\rm{S}}}/{\lambda} $ 
图 2 Si111双晶单色器的第二晶和Si111分析晶体构成(+1, –1)型无色散配置的实验配置图. [111]是衍射面法线的晶向
Figure 2. The experimental configuration of (+1, –1) type non-dispersive consists of the second crystal of Si111-DCM and Si111 analyzer. The[111] is the crystal direction of the normal of the diffraction plane.
图 3 Si111双晶单色器的第二晶和Si111分析晶体构成(+1, +1)型色散配置的实验配置图
Figure 3. The experimental configuration of (+1, +1) type dispersive consists of the second crystal of Si111-DCM and Si111 analyzer.
图 4 (a)和(b)分别为无色散(+1, –1)配置和色散(+1, +1)配置条件下, 分析晶体扫描单色器出射光过程的DuMond图. 斜线区域是双晶单色器的DuMond窗口, 圆点的区域是分析晶体的DuMond窗口
Figure 4. DuMond diagrams during scanning the output beam of DCM by analyzer. Panel (a) represents the non-dispersive (+1, –1) configuration and panel (b) represents the dispersive (+1, +1) configuration. The oblique line region is the DuMond window of the DCM. The point region is the DuMond window of the analyzer.
图 5 Si111双晶单色器的第二晶和Si333分析晶体构成(+1, –3)型色散配置的实验配置图
Figure 5. The experimental configuration of (+1, –3) type dispersive consists of the second crystal of Si111-DCM and Si333 analyzer.
图 6 Si111双晶单色器的第二晶和Si333分析晶体构成(+1, +3)型色散配置的实验配置图
Figure 6. The experimental configuration of (+1, +3) type dispersive consists of the second crystal of Si111-DCM and Si333 analyzer.
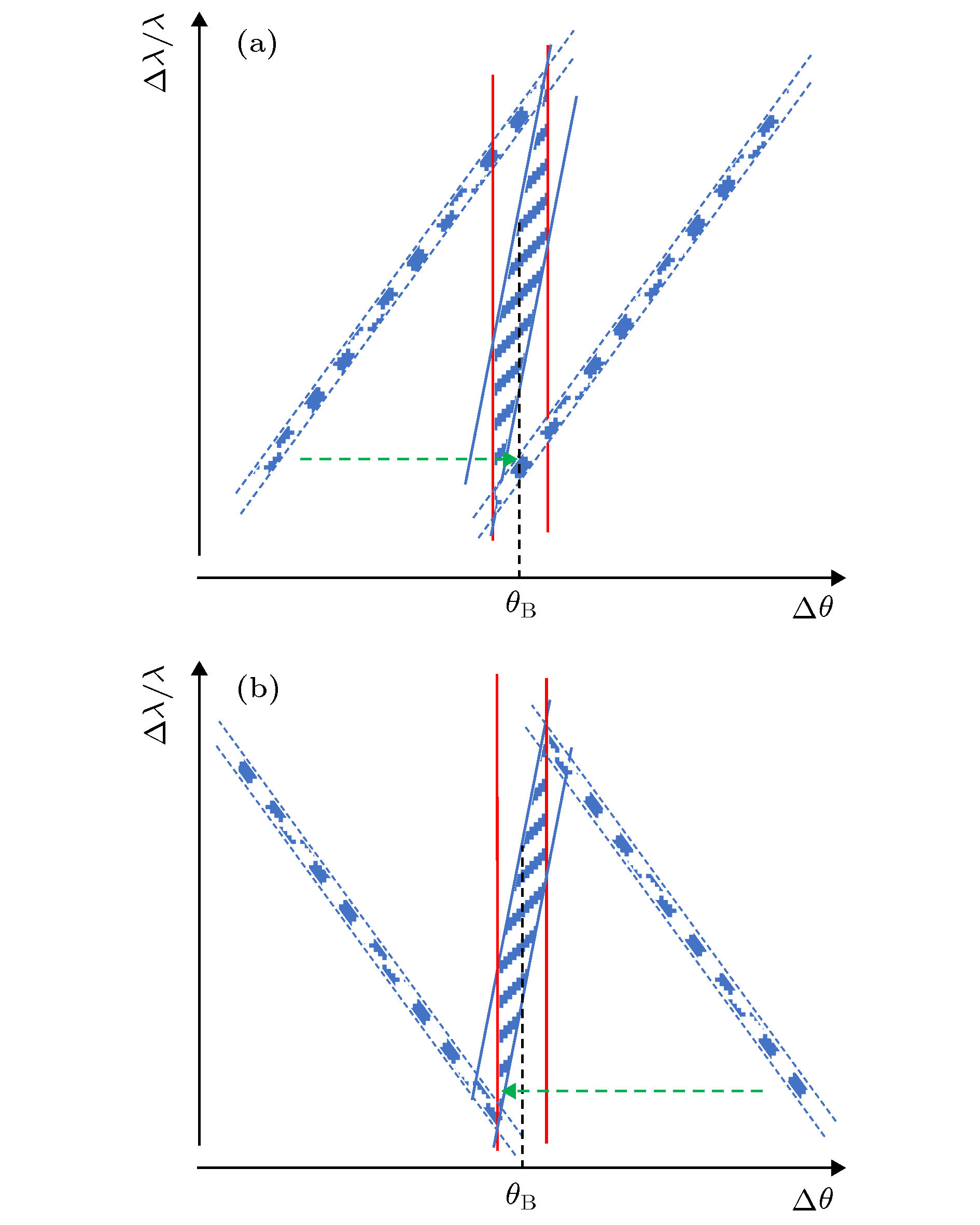
图 7 (a)和(b)分别为使用Si333做分析晶体的(+1, –3)型和(+1, +3)型色散配置, 扫描单色器出射光过程的DuMond图. 绿色虚线箭头指示了扫描过程, 两个圆点的区域给出了分析晶体DuMond窗口起止位置
Figure 7. DuMond diagrams during scanning the output beam of DCM by Si(333) analyzer. Panel (a) and (b) represent the (+1, –3) typeand (+1, +3) type dispersive configuration, respectively. The green dotted arrow indicates the scanning process. The two point-regions give the starting and ending position of the DuMond window of the analyzer.
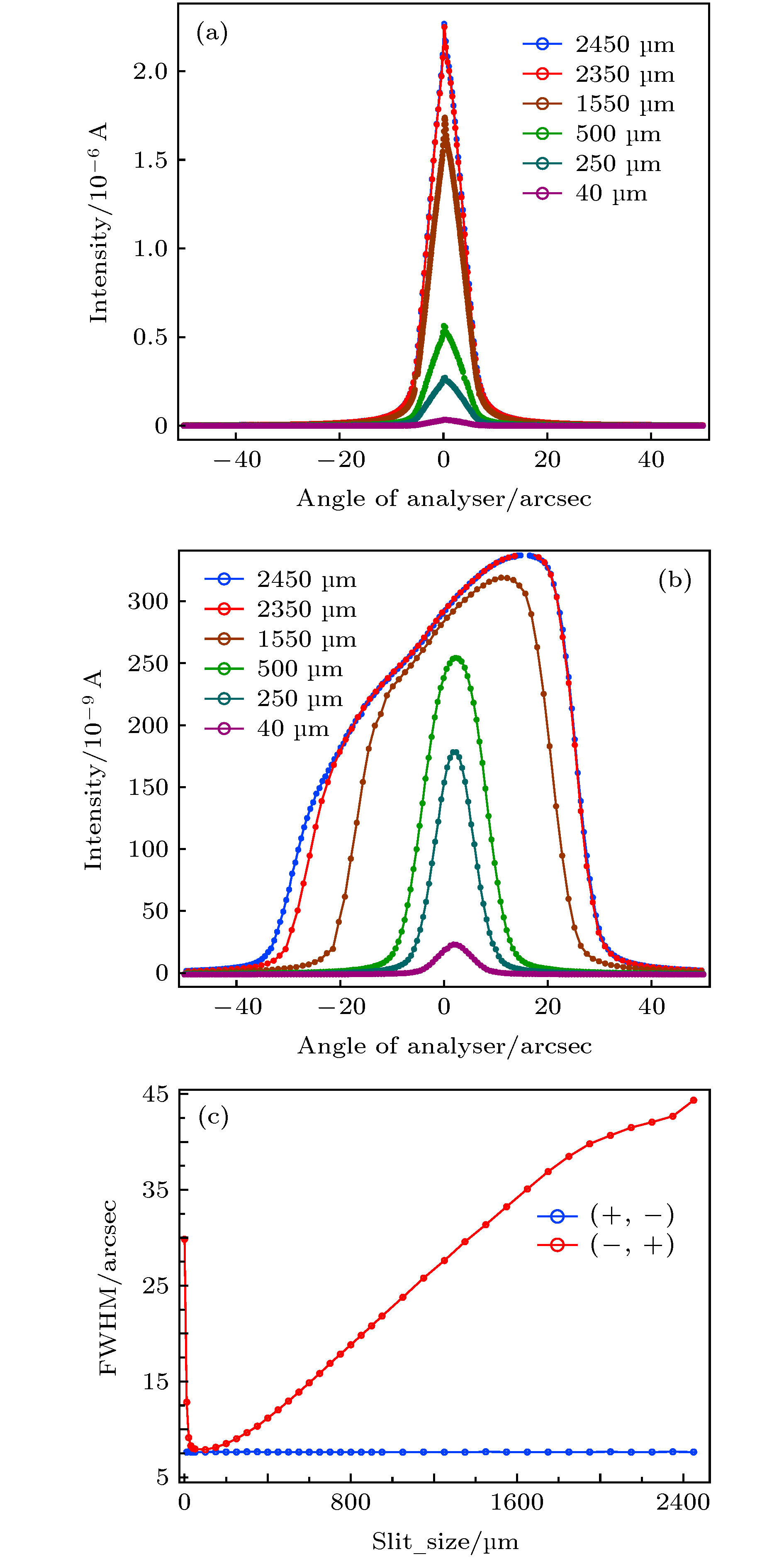
图 8 (a)和(b)分别为无色散配置和“固定”色散配置条件下不同狭缝纵向宽度时Si111分析器的摇摆曲线. (c)是无色散配置和“固定”色散配置条件下随狭缝宽度调节时摇摆曲线的半高宽的曲线
Figure 8. (a) and (b) give the rocking curves of the Si (111) analyzer with different slit vertical widths under the conditions of non-dispersion configuration and “fixed dispersion” configuration, respectively. (c) gives the FWHM curve of the rocking curve when the slit vertical width is adjusted under the condition of non-dispersion configuration and “fixed dispersion” configuration.
图 9 (a)和(b)分别为使用Si111做分析器时, (+1, –1)和(+1, +1)实验配置条件下摇摆曲线做差分后的结果. 横轴的坐标原点对应着10 keV时分析晶体的衍射角. (b)同时还是在“固定”色散排列条件下使用Si111做分析器得到的未经狭缝(角度)——波长转换的“赝”DuMond图. 从图中可以直接读取不同狭缝宽度下得到的摇摆曲线半高宽的测量值
Figure 9. (a) and (b) show the results of slit width difference of rocking curve with (+1, –1) and (+1, +1) experimental configurations with Si111 analyzer, respectively. The coordinate origin of the transverse axis corresponds to the diffraction angle of the analytic crystal at 10 keV. Also, (b) is the DuMond diagram without slit (angle) - wavelength conversion obtained using Si111 analyzer under the condition of dispersion configuration. The measured values of rocking curve FWHM with different slit widths can be read directly from the figure.
图 10 (a)和(b)分别为使用Si333做分析器时, 在(+1, –3)型和(+1, +3)型实验配置条件下得到的“赝” DuMond图
Figure 10. (a) and (b) give the pseudo DuMond diagram using Si333 analyzer under the condition of (+1, –3) type and (+1, +3) type dispersion configuration, respectively.
表 1 不同实验配置得到的实验值以及退分析器卷积和色散展宽后的值. 单位: 角秒(″)
Table 1. The experimental values obtained from different experimental configurations and the values after deconvolution of the analyzer and removal of dispersion broadening. Unit: arcsec.
分析器衍射面 实验配置 色散类别 测量值 退卷积和色散展宽值 理论值 备注 (111) (+n, –n) 无色散 7.64(4) 5.40(4) 5.38 双晶单色器带宽 (+n, +n) “固定”色散 52(1) 26(1) (333) (+n, –m) “弱”色散 67(1) 26(1) 25.8 光束的带宽 (+n, +m) “强”色散 117(1) 26(1) 
DownLoad: CSV
-
[1] Jiang X M, Zheng W L, Wu J, Jing Y, Liu G 1995 Rev. Sci. Instrum. 66 1694
Google Scholar
[2] Zhang Z Y, Chen M, Tong Y J, Ji T, Zhu H C, Peng W W, Zhang M, Li Y J, Xiao T Q 2014 Infrared Phy. Tech. 67 521
Google Scholar
[3] Fischetti R F, Yoder D W, Xu S L, et al. 2007 9th International Conference on Synchrotron Radiation Instrumentation Daegu, Korea, May 28–June 2, 2006 p754
[4] Yu H S, Wei X J, Li J, et al. 2015 Nucl. Sci. Tech. 26 4
Google Scholar
[5] Liermann H P, Konopkova Z, Morgenroth W, et al. 2015 J. Synchrotron Rad. 22 908
Google Scholar
[6] Tian F, Li X H, Wang Y Z, et al. 2015 Nucl. Sci. Tech. 26 1
Google Scholar
[7] Yamaoka H, Hiraoka N, Ito M, et al. 2000 J. Synchrotron Rad. 7 69
Google Scholar
[8] Dippel A C, Liermann H P, Delitz J T, et al. 2015 J. Synchrotron Rad. 22 675
Google Scholar
[9] Seto M, Yoda Y, Kikuta S 1995 Phys. Rev. Lett. 74 3828
Google Scholar
[10] Zhang X, Mochizuki T, Sugiyama H 1992 Rev. Sci. Instrum. 63 404
Google Scholar
[11] Beaumont J H, Hart M 1974 J. Phys. E: Sci. Intum. 7 823
Google Scholar
[12] Zhang X, Hiroyuki F 2006 Jpn. J. Appl. Phys. 45 7933
Google Scholar
[13] Yang T Y, Wen W, Yin G Z, et al. 2015 Nucl. Sci. Tech. 26 20101
Google Scholar
[14] Wang S S, Kong R H, Shan X B, et al. 2006 J. Synchrotron Rad. 13 415
Google Scholar
[15] Puik E J, Dorssen G E, Eiel K J 1991 J. Vac. Sci. Technol. A: Vacuum, Surfaces, and Films 9 3142
Google Scholar
[16] Gong X, Lu Q 2015 J. X-ray Sci. Technol 23 409
Google Scholar
[17] DuMond J W M 1937 Phys. Rev. 52 872
Google Scholar
[18] Zhao Z T, Xu H J 2004 Proceedings of European Particle Accelerator Conference Lucerne, Switzerland, June 5–9, 2004 p2368
[19] Batterman B W, Cole H 1964 Rev. M. Phys. 36 682
Google Scholar
[20] Punegov V L, Pavlov K M, Karpov A V 2017 J. Appl. Cryst. 50 1256
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 10379
- PDF Downloads: 134
- Cited By: 0
