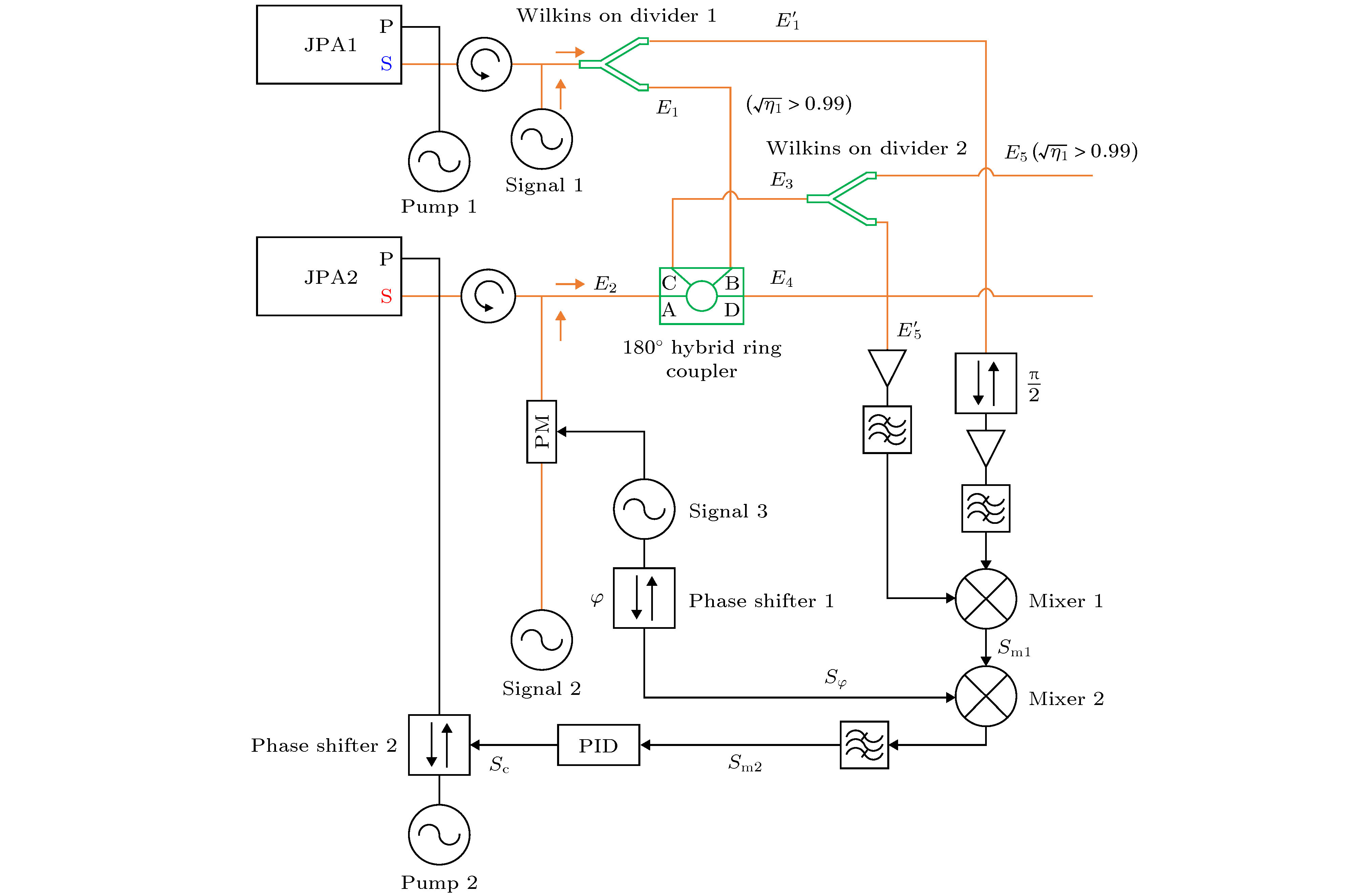
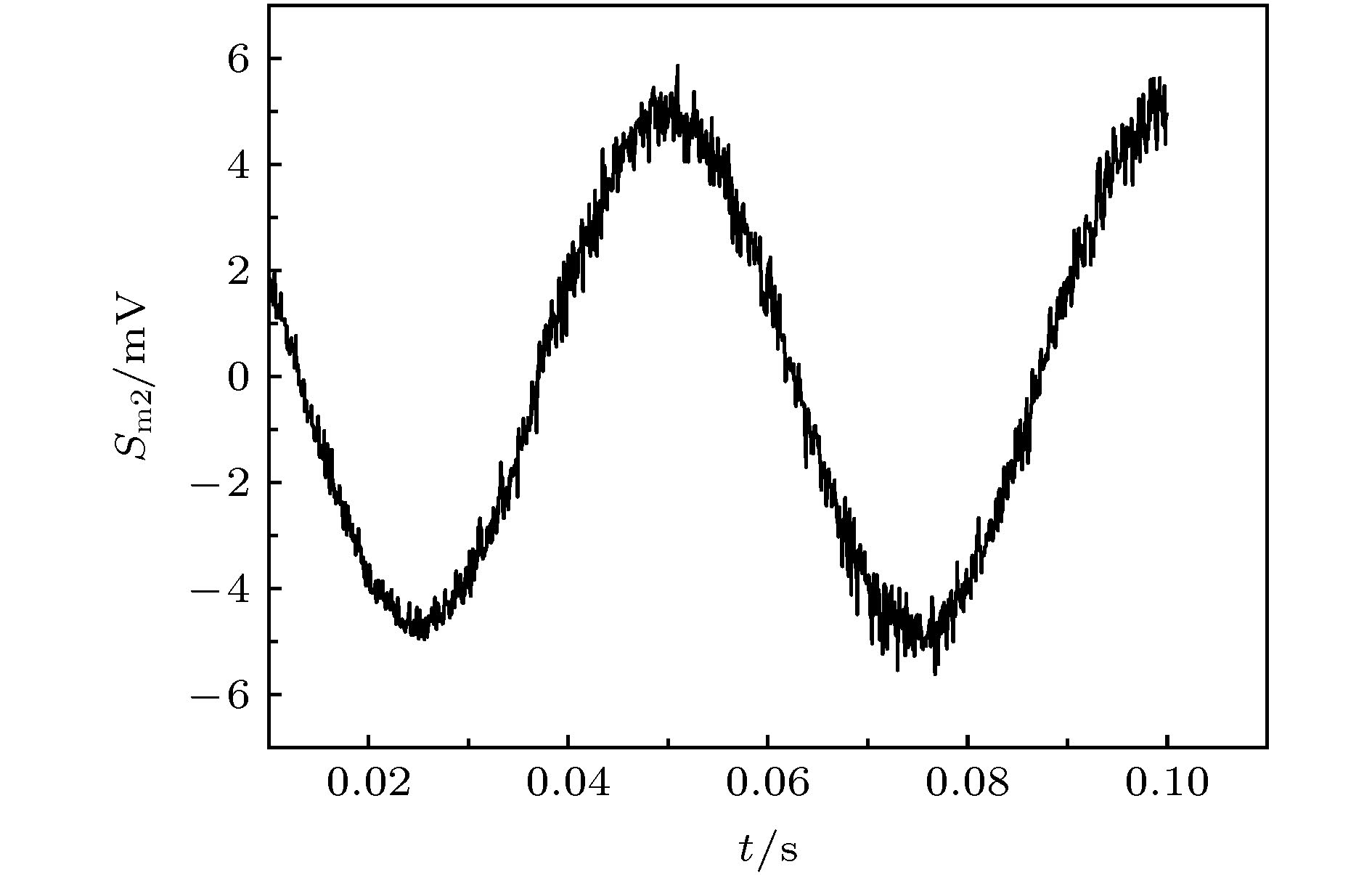
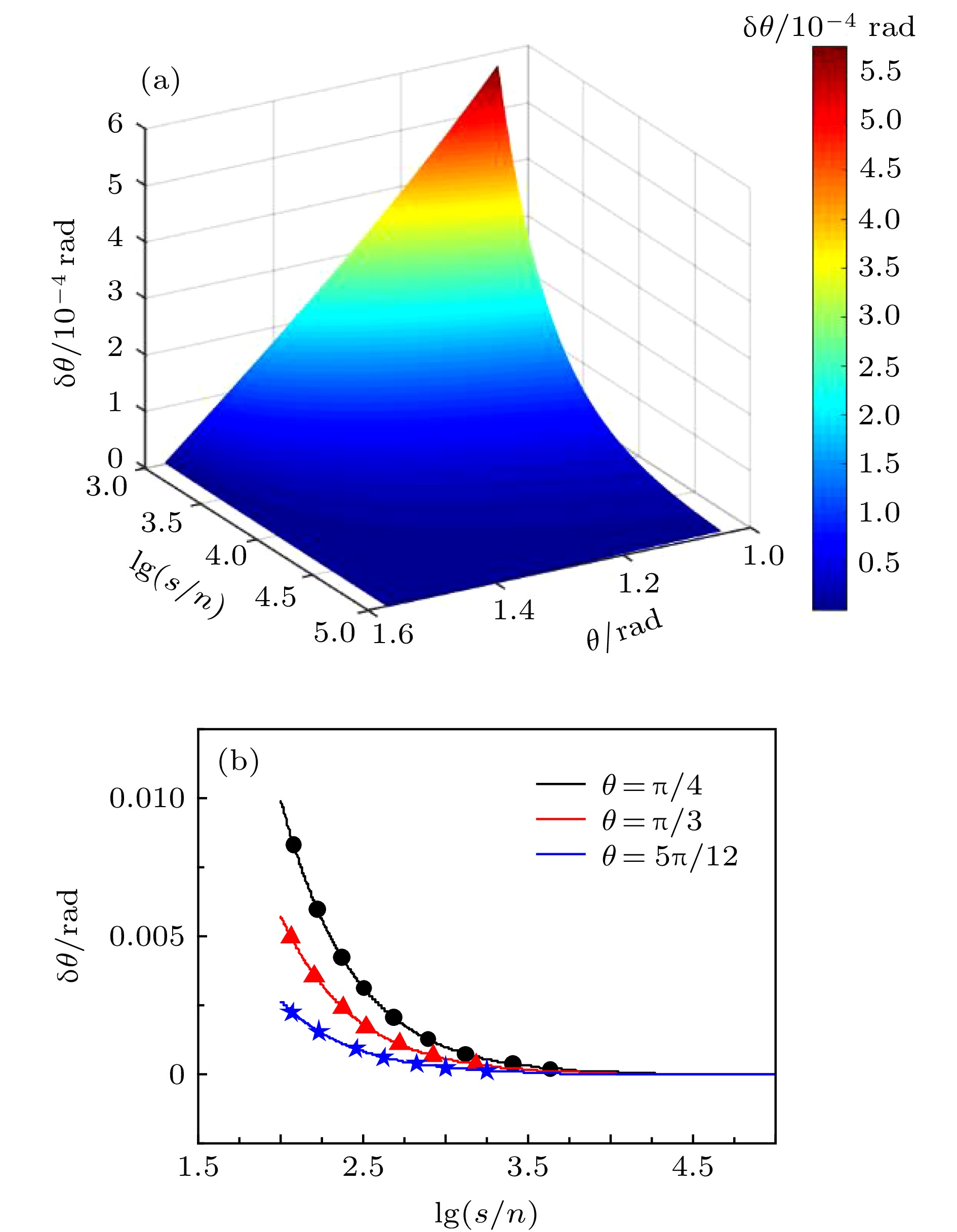
-
As the core of quantum entanglement, two-mode squeezing is manifested in cross-correlations of incompatible observables between two subsystems, which makes the two-mode squeezed microwave an ideal resource for applications in quantum communication, quantum illumination, and quantum microwave navigation. Currently the preparation scheme of two-mode squeezed microwave, based on the Josephson parametric amplifier (JPA) and a superconducting 180° hybrid ring coupler, proves to be the most efficient and excellent in quantum properties. Nevertheless, the difficult phase locking processing restricts the further improvement of entanglement. There is no effective solution but the dual-path receiver with phase stabilization measures, and the phase error reaches as high as 0.3°, which still does not meet the requirements for phase locking precision and entanglement stability. To overcome the academic obstacle, we propose a phase locking scheme to achieve a stable two-mode squeezed microwave. There are two JPAs used to separately generate single-mode squeezed microwaves, between which the difference lies in the fact that the input of one JPA is phase-modulated but the other is not. A superconducting 180° hybrid ring coupler is used to distribute the two single-mode squeezed microwaves into two output paths, which are two-mode squeezing if the squeezing directions of the two single-mode squeezed microwave are orthogonal. That is to say, the relative phase satisfies the condition
$\theta = {\text{π}}/2$ . By mixing the unmodulated single-mode squeezed microwave and one output of the superconducting 180° hybrid ring coupler, a relative phase is obtained in subsequent process. Proportional integral derivative (PID) controller is used as the input of phase error, and the output is used to adjust the pump phase of JPA, which is the key to phase locking and stable two-mode squeezing. The present research not only provides an effective strategy to achieve stable two-mode squeezed microwave, but also may attract more attention to the precisive measurement of two-mode squeezed microwave.-
Keywords:
- two-mode squeezed microwave /
- phase locking
[1] Braunstein S L, Loock P V 2005 Rev. Mod. Phys. 77 513
Google Scholar
[2] Weedbrook C, Pirandola S, Garcia-Patron R, Cerf N J, Ralph T C, Shapiro J H, Lloyd S 2012 Rev. Mod. Phys. 84 621
Google Scholar
[3] Einstein A, Podolsky B, Rosen N 1935 Phys. Rev. 47 777
Google Scholar
[4] Liu C C, Wang D, Sun W Y, Ye L 2017 Quantum Inf. Process. 16 219
Google Scholar
[5] 苗强, 李响, 吴德伟, 罗均文, 魏天丽, 朱浩男 2019 68 070302
Google Scholar
Miao Q, Li X, Wu D W, Luo J W, Wei T L, Zhu H N 2019 Acta Phys. Sin. 68 070302
Google Scholar
[6] Hofheinz M, Huard B, Portier F 2016 C. R. Physique 17 679
Google Scholar
[7] Sanz M, las Heras U, García-Ripoll J J, Solano E, di Candia R 2017 Phys. Rev. Lett. 118 070803
Google Scholar
[8] Madsen L S, Usenko V C, Lassen M, Filip R, Andersen U L 2012 Nat. Commun. 3 1083
Google Scholar
[9] di Candia R, Fedorov K G, Zhong L, Felicetti S, Menzel E P, Sanz M, Deppe F, Marx A, Gross R, Solano E 2015 EPJ Quantum Technol. 2 25
Google Scholar
[10] las Heras U, di Candia R D, Fedorov K G, Deppe F, Sanz M, Solano E 2017 Sci. Rep. 7 9333
Google Scholar
[11] Barzanjeh S, Guha S, Weedbrook C, Vitali D, Shapiro J H, Pirandola S 2015 Phys. Rev. Lett. 114 080503
Google Scholar
[12] Li X, Wu D W, Miao Q, Zhu H N, Wei T L 2018 IEEE Photonics J. 10 6101107
[13] Li X, Wu D W, Wei T L, Miao Q, Zhu H N, Yang C Y 2018 AIP Adv. 8 065217
Google Scholar
[14] Castellanos-Beltran M A, Irwin K D, Hilton G C, Vale L R, Lehnert K W 2008 Nat. Phys. 4 929
Google Scholar
[15] Menzel E P, Candia R D, Deppe F, Eder P, Zhong L, Haeberlein M, Baust A, Hoffmann E, Ballester D, Inomata K, Yamamoto T, Nakamura Y, Solano E, Marx1 A, Ihmig M, Gross R 2012 Phys. Rev. Lett. 109 250502
Google Scholar
[16] Fedorov K G, Pogorzalek S, Heras U L, Sanz M, Yard P, Eder P, Fischer M, Goetz J, Xie1 E, Inomata K, Nakamura Y, di Candia R, Solano E, Marx1 A, Deppe1 F, Gross R 2018 Sci. Rep. 8 6416
Google Scholar
[17] Pogorzalek S, Fedorov K G, Xu M, Parra-Rodriguez A, Sanz M, Fischer M, Xie E, Inomata K, Nakamura Y, Solano E, Marx1 A, Deppe1 F, Gross R 2019 Nature Commun. 10 2604
Google Scholar
[18] Li P B, Li F L 2011 Opt. Commun. 284 294
Google Scholar
[19] Ockeloen-Korppi C F., Damskägg E, Pirkkalainen J M, Heikkilä T T, Massel F, Sillanpää M A 2017 Phys. Rev. Lett. 118 103601
Google Scholar
[20] Abdi M, Tombesi P, Vitali D 2015 Ann. Phys. 527 139
Google Scholar
[21] Sete E A, Eleuch H 2014 Phys. Rev. A 89 013841
Google Scholar
[22] Marković D, Pillet J D, Flurin E, Roch N, Huard B 2019 Phys. Rev. Applied 12 024034
Google Scholar
[23] Duan L M, Giedke G, Cirac J I, Zoller P 1999 Phys. Rev. Lett. 84 2722
[24] Li X, Wu D W, Zhu H N, Miao Q, Wei T L 2018 Results Phys. 11 920
Google Scholar
-
图 1 双模压缩微波制备方案原理图
Figure 1. Schematic of two-mode squeezed microwave preparation scheme.
图 2 双模压缩微波制备的相位锁定方案原理图
Figure 2. Schematic of phase locking scheme for two-mode squeezed microwave preparation.
图 3 扫描
$\theta $ 时的鉴频曲线.Figure 3. Frequency discrimination curve when scanning
$\theta $ .
图 4 相位锁定示意图.
Figure 4. Schematic of phase locking process.
图 5 相位误差与输出信噪比及自身相位值的变化关系
Figure 5. Variance of
$\text{δ}\theta $ versus${s/n}$ and$\theta $ .
图 6
${\text δ}{E_N}$ 与相位误差${\text δ}\theta $ 及压缩度r的关系Figure 6. Variance of
${\text δ}{E_N}$ versus${\text δ}\theta $ and r.
图 7
${\text δ}{E_N}/{E_N}$ 与相位误差${\rm{\delta }}\theta $ 及压缩度r的关系图Figure 7. Variance of
${{{\rm{\delta }}{E_N}}/{{E_N}}}$ versus${\rm{\delta }}\theta $ and r. -
[1] Braunstein S L, Loock P V 2005 Rev. Mod. Phys. 77 513
Google Scholar
[2] Weedbrook C, Pirandola S, Garcia-Patron R, Cerf N J, Ralph T C, Shapiro J H, Lloyd S 2012 Rev. Mod. Phys. 84 621
Google Scholar
[3] Einstein A, Podolsky B, Rosen N 1935 Phys. Rev. 47 777
Google Scholar
[4] Liu C C, Wang D, Sun W Y, Ye L 2017 Quantum Inf. Process. 16 219
Google Scholar
[5] 苗强, 李响, 吴德伟, 罗均文, 魏天丽, 朱浩男 2019 68 070302
Google Scholar
Miao Q, Li X, Wu D W, Luo J W, Wei T L, Zhu H N 2019 Acta Phys. Sin. 68 070302
Google Scholar
[6] Hofheinz M, Huard B, Portier F 2016 C. R. Physique 17 679
Google Scholar
[7] Sanz M, las Heras U, García-Ripoll J J, Solano E, di Candia R 2017 Phys. Rev. Lett. 118 070803
Google Scholar
[8] Madsen L S, Usenko V C, Lassen M, Filip R, Andersen U L 2012 Nat. Commun. 3 1083
Google Scholar
[9] di Candia R, Fedorov K G, Zhong L, Felicetti S, Menzel E P, Sanz M, Deppe F, Marx A, Gross R, Solano E 2015 EPJ Quantum Technol. 2 25
Google Scholar
[10] las Heras U, di Candia R D, Fedorov K G, Deppe F, Sanz M, Solano E 2017 Sci. Rep. 7 9333
Google Scholar
[11] Barzanjeh S, Guha S, Weedbrook C, Vitali D, Shapiro J H, Pirandola S 2015 Phys. Rev. Lett. 114 080503
Google Scholar
[12] Li X, Wu D W, Miao Q, Zhu H N, Wei T L 2018 IEEE Photonics J. 10 6101107
[13] Li X, Wu D W, Wei T L, Miao Q, Zhu H N, Yang C Y 2018 AIP Adv. 8 065217
Google Scholar
[14] Castellanos-Beltran M A, Irwin K D, Hilton G C, Vale L R, Lehnert K W 2008 Nat. Phys. 4 929
Google Scholar
[15] Menzel E P, Candia R D, Deppe F, Eder P, Zhong L, Haeberlein M, Baust A, Hoffmann E, Ballester D, Inomata K, Yamamoto T, Nakamura Y, Solano E, Marx1 A, Ihmig M, Gross R 2012 Phys. Rev. Lett. 109 250502
Google Scholar
[16] Fedorov K G, Pogorzalek S, Heras U L, Sanz M, Yard P, Eder P, Fischer M, Goetz J, Xie1 E, Inomata K, Nakamura Y, di Candia R, Solano E, Marx1 A, Deppe1 F, Gross R 2018 Sci. Rep. 8 6416
Google Scholar
[17] Pogorzalek S, Fedorov K G, Xu M, Parra-Rodriguez A, Sanz M, Fischer M, Xie E, Inomata K, Nakamura Y, Solano E, Marx1 A, Deppe1 F, Gross R 2019 Nature Commun. 10 2604
Google Scholar
[18] Li P B, Li F L 2011 Opt. Commun. 284 294
Google Scholar
[19] Ockeloen-Korppi C F., Damskägg E, Pirkkalainen J M, Heikkilä T T, Massel F, Sillanpää M A 2017 Phys. Rev. Lett. 118 103601
Google Scholar
[20] Abdi M, Tombesi P, Vitali D 2015 Ann. Phys. 527 139
Google Scholar
[21] Sete E A, Eleuch H 2014 Phys. Rev. A 89 013841
Google Scholar
[22] Marković D, Pillet J D, Flurin E, Roch N, Huard B 2019 Phys. Rev. Applied 12 024034
Google Scholar
[23] Duan L M, Giedke G, Cirac J I, Zoller P 1999 Phys. Rev. Lett. 84 2722
[24] Li X, Wu D W, Zhu H N, Miao Q, Wei T L 2018 Results Phys. 11 920
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 7339
- PDF Downloads: 69
- Cited By: 0
